原子核外电子排布的量子规律:从薛定谔方程到电子排布——薛定谔方程在球坐标系下的求解
目录
- 1. 引言:原子结构理论的量子力学基础
- 2. 薛定谔方程及其求解
- 2.1 薛定谔方程的基本形式
- 2.2 球坐标系下的薛定谔方程
- 3. 变量分离求解
- 3.1 **方位角方程**:
- 3.2 **极角方程**:
- 3.3 **径向方程**:
- 3.4 球谐函数
- 4. 完整波函数与量子数
- 5. 量子数的自然出现
- 6. 原子轨道与电子云
- 6.1 原子轨道的图像表示
- 6.2 电子云
- 7. 泡利不相容原理的物理内涵
- 7.1 历史背景与发现过程
- 7.2 基本原理与数学表述
- 7.3 物理意义与深远影响
- 8. 洪特规则的物理内涵
- 8.1 经验规律与量子解释
- 8.2 数学表述与能量优化
- 8.3 物理意义与应用
- 9. 两大原理的协同作用与原子结构
- 9.1 电子排布三原则的协同
- 9.2 原子核外电子排布实例分析
- 碳原子(C, Z=6)
- 氮原子(N, Z=7)
- 铬原子(Cr, Z=24)的特例
- 10. 多电子原子体系的薛定谔方程没有精确解
- 11. 总结
1. 引言:原子结构理论的量子力学基础
写这篇博客的目的是为解释物质自身磁性打基础,同时为致力于学习半导体物理的同学建立基础,并为可能对化学等有兴趣的网友,建立必要的量子化学基础知识。总之理解原子核外电子排布的量子规律,是理解和学习很多宏观物理、化学现象的必要基础。当然读这篇文章需要一定的数学基础,如果数学基础不强,可以跳过公式,直接关注一些概念和结论即可,以能理解多少为限进行阅读即可。
原子结构理论的发展经历了从道尔顿的实心小球模型到汤姆逊的葡萄干布丁模型,再到卢瑟福的行星模型和玻尔的量子化轨道模型。然而,这些经典模型无法完全解释原子光谱的精细结构和多电子原子行为。1926年,薛定谔提出了著名的薛定谔方程,建立了描述微观粒子运动的量子力学理论,从而能够更精确地描述核外电子的运动状态。
量子力学认为,电子具有波粒二象性,其运动状态不能用经典的轨道概念来描述,而只能用概率的方式来描述。原子核外的电子运动状态由四个量子数决定,电子的排布遵循一系列量子规则,包括泡利不相容原理、能量最低原理和洪特规则。
2. 薛定谔方程及其求解
2.1 薛定谔方程的基本形式
薛定谔方程是描述微观粒子运动的基本波动方程,其一般形式为定态薛定谔方程:
− ℏ 2 2 m ∇ 2 ψ + V ψ = E ψ \rm -\cfrac{\hbar^2}{2m}\nabla^2\psi + V\psi = E\psi −2mℏ2∇2ψ+Vψ=Eψ
其中, ψ \psi ψ 是波函数, E \rm E E是体系的总能量, V \rm V V 是势能, m \rm m m 是粒子的质量, ℏ \rm \hbar ℏ 是约化普朗克常数( ℏ = h / 2 π \rm \hbar = h/2\pi ℏ=h/2π), ∇ 2 \nabla^2 ∇2 是拉普拉斯算符。
对于氢原子体系,势能项 V \rm V V 表示原子核与电子之间的库仑引力: V = − Z e 2 4 π ϵ 0 r \rm V = -\cfrac{Ze^2}{4\pi\epsilon_0 r} V=−4πϵ0rZe2,其中 Z \rm Z Z 是原子序数, e \rm e e 是元电荷, r \rm r r 是电子与核的距离。
2.2 球坐标系下的薛定谔方程
单电子原子(如氢原子)的定态薛定谔方程为:
[ − ℏ 2 2 μ ∇ 2 + V ( r ) ] ψ = E ψ \rm \left[ -\cfrac{\hbar^2}{2\mu} \nabla^2 + V(r) \right] \psi = E \psi [−2μℏ2∇2+V(r)]ψ=Eψ
其中:
- $ \mu $ 为电子-原子核的约化质量,
- V ( r ) = − Z e 2 4 π ϵ 0 r \rm V(r) = -\cfrac{Ze^2}{4\pi\epsilon_0 r} V(r)=−4πϵ0rZe2 为库仑势($ Z $ 为原子序数),
- ∇ 2 \nabla^2 ∇2 为拉普拉斯算符。
在球坐标系中,拉普拉斯算符表示为:
∇ 2 = 1 r 2 ∂ ∂ r ( r 2 ∂ ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 ∂ ϕ 2 \rm \nabla^2 = \cfrac{1}{r^2} \cfrac{\partial}{\partial r} \left( r^2 \cfrac{\partial}{\partial r} \right) + \cfrac{1}{r^2 \sin\theta} \cfrac{\partial}{\partial \theta} \left( \sin\theta \cfrac{\partial}{\partial \theta} \right) + \cfrac{1}{r^2 \sin^2\theta} \cfrac{\partial^2}{\partial \phi^2} ∇2=r21∂r∂(r2∂r∂)+r2sinθ1∂θ∂(sinθ∂θ∂)+r2sin2θ1∂ϕ2∂2
代入薛定谔方程,得:
1 r 2 ∂ ∂ r ( r 2 ∂ ψ ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ ψ ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 ψ ∂ ϕ 2 + 2 μ ℏ 2 ( E + Z e 2 4 π ϵ 0 r ) ψ = 0 \rm \cfrac{1}{r^2} \cfrac{\partial}{\partial r} \left( r^2 \cfrac{\partial \psi}{\partial r} \right) + \cfrac{1}{r^2 \sin\theta} \cfrac{\partial}{\partial \theta} \left( \sin\theta \cfrac{\partial \psi}{\partial \theta} \right) + \cfrac{1}{r^2 \sin^2\theta} \cfrac{\partial^2 \psi}{\partial \phi^2} + \cfrac{2\mu}{\hbar^2} \left( E + \cfrac{Ze^2}{4\pi\epsilon_0 r} \right) \psi = 0 r21∂r∂(r2∂r∂ψ)+r2sinθ1∂θ∂(sinθ∂θ∂ψ)+r2sin2θ1∂ϕ2∂2ψ+ℏ22μ(E+4πϵ0rZe2)ψ=0
此方程可通过变量分离法求解。
3. 变量分离求解
设波函数为 ψ ( r , θ , ϕ ) = R ( r ) Θ ( θ ) Φ ( ϕ ) \rm \psi(r, \theta, \phi) = R(r) \Theta(\theta) \Phi(\phi) ψ(r,θ,ϕ)=R(r)Θ(θ)Φ(ϕ),代入方程并分离变量:
3.1 方位角方程:
代入后,得到 Φ ( ϕ ) \Phi(\phi) Φ(ϕ) 的方程:
d 2 Φ d ϕ 2 + m 2 Φ = 0 \rm \cfrac{d^2 \Phi}{d\phi^2} + m^2 \Phi = 0 dϕ2d2Φ+m2Φ=0
解为:
Φ m ( ϕ ) = 1 2 π e i m ϕ \rm \Phi_m(\phi) = \cfrac{1}{\sqrt{2\pi}} e^{im\phi} Φm(ϕ)=2π1eimϕ
其中 m m m 为整数,即磁量子数,满足周期性边界条件 Φ ( ϕ + 2 π ) = Φ ( ϕ ) \Phi(\phi + 2\pi) = \Phi(\phi) Φ(ϕ+2π)=Φ(ϕ)(故 m = 0 , ± 1 , ± 2 , … \rm m = 0, \pm 1, \pm 2, \ldots m=0,±1,±2,…)。
3.2 极角方程:
分离出 Θ ( θ ) \Theta(\theta) Θ(θ) 的方程:
1 sin θ d d θ ( sin θ d Θ d θ ) + [ l ( l + 1 ) − m 2 sin 2 θ ] Θ = 0 \rm \cfrac{1}{\sin\theta} \cfrac{d}{d\theta} \left( \sin\theta \cfrac{d\Theta}{d\theta} \right) + \left[ l(l+1) - \cfrac{m^2}{\sin^2\theta} \right] \Theta = 0 sinθ1dθd(sinθdθdΘ)+[l(l+1)−sin2θm2]Θ=0
令 $\rm u = \cos\theta $,方程化为缔合勒让德方程:
d d u [ ( 1 − u 2 ) d Θ d u ] + [ l ( l + 1 ) − m 2 1 − u 2 ] Θ = 0 \rm \cfrac{d}{du} \left[ (1-u^2) \cfrac{d\Theta}{du} \right] + \left[ l(l+1) - \cfrac{m^2}{1-u^2} \right] \Theta = 0 dud[(1−u2)dudΘ]+[l(l+1)−1−u2m2]Θ=0
解为缔合勒让德多项式 P l m ( cos θ ) \rm P_l^m (\cos\theta) Plm(cosθ),其中 l \rm l l 为角量子数( l = 0 , 1 , 2 , … \rm l = 0, 1, 2, \ldots l=0,1,2,…,且 ∣ m ∣ ≤ l \rm |m| \leq l ∣m∣≤l)。归一化解为:
Θ l , m ( θ ) = ( 2 l + 1 ) ( l − ∣ m ∣ ) ! 2 ( l + ∣ m ∣ ) ! P l ∣ m ∣ ( cos θ ) \rm \Theta_{l,m}(\theta) = \sqrt{\cfrac{(2l+1)(l-|m|)!}{2(l+|m|)!}} P_l^{|m|} (\cos\theta) Θl,m(θ)=2(l+∣m∣)!(2l+1)(l−∣m∣)!Pl∣m∣(cosθ)
3.3 径向方程:
剩余部分为径向方程:
d d r ( r 2 d R d r ) + 2 μ r 2 ℏ 2 ( E + Z e 2 4 π ϵ 0 r ) R = l ( l + 1 ) R \rm \cfrac{d}{dr} \left( r^2 \cfrac{dR}{dr} \right) + \cfrac{2\mu r^2}{\hbar^2} \left( E + \cfrac{Ze^2}{4\pi\epsilon_0 r} \right) R = l(l+1) R drd(r2drdR)+ℏ22μr2(E+4πϵ0rZe2)R=l(l+1)R
引入变量代换 $\rm \rho = \alpha r ( ( (\rm \alpha = \sqrt{-8\mu E / \hbar^2} $,因 E < 0 \rm E < 0 E<0),方程简化为:
d 2 u d ρ 2 + [ λ ρ − 1 4 − l ( l + 1 ) ρ 2 ] u = 0 \rm \cfrac{d^2 u}{d\rho^2} + \left[ \cfrac{\lambda}{\rho} - \cfrac{1}{4} - \cfrac{l(l+1)}{\rho^2} \right] u = 0 dρ2d2u+[ρλ−41−ρ2l(l+1)]u=0
其中 $\rm u(\rho) = \rho R(\rho) , , ,\rm \lambda = \cfrac{Ze^2}{4\pi\epsilon_0 \hbar} \sqrt{-\cfrac{\mu}{2E}} $。
解为拉盖尔多项式,要求解满足边界条件( r → ∞ \rm r \to \infty r→∞ 时 $\rm R \to 0 $),可得能量量子化:
E n = − μ Z 2 e 4 32 π 2 ϵ 0 2 ℏ 2 n 2 = − 13.6 Z 2 n 2 eV \rm E_n = -\cfrac{\mu Z^2 e^4}{32\pi^2 \epsilon_0^2 \hbar^2 n^2} = -\cfrac{13.6 Z^2}{n^2} \text{eV} En=−32π2ϵ02ℏ2n2μZ2e4=−n213.6Z2eV
径向波函数为:
R n , l ( r ) = ( 2 Z n a 0 ) 3 ( n − l − 1 ) ! 2 n [ ( n + l ) ! ] 3 e − ρ / 2 ρ l L n − l − 1 2 l + 1 ( ρ ) \rm R_{n,l}(r) = \sqrt{ \left( \cfrac{2Z}{n a_0} \right)^3 \cfrac{(n-l-1)!}{2n[(n+l)!]^3} } e^{-\rho/2} \rho^l L_{n-l-1}^{2l+1}(\rho) Rn,l(r)=(na02Z)32n[(n+l)!]3(n−l−1)!e−ρ/2ρlLn−l−12l+1(ρ)
其中 a 0 = 4 π ϵ 0 ℏ 2 μ e 2 \rm a_0 = \cfrac{4\pi\epsilon_0 \hbar^2}{\mu e^2} a0=μe24πϵ0ℏ2 为玻尔半径, L \rm L L 为拉盖尔多项式。
3.4 球谐函数
将 Θ ( θ ) \Theta(\theta) Θ(θ) 和 Φ ( ϕ ) \Phi(\phi) Φ(ϕ) 的解合并,并归一化后,得到球谐函数 Y l m ( θ , ϕ ) \rm Y_l^m(\theta, \phi) Ylm(θ,ϕ),它是角动量平方算符 L ^ 2 \rm \hat{L}^2 L^2和角动量z分量算符 L ^ z \hat{L}_z L^z的共同本征函数:
Y l m ( θ , ϕ ) = ε 2 l + 1 4 π ( l − ∣ m ∣ ) ! ( l + ∣ m ∣ ) ! e i m ϕ P l ∣ m ∣ ( cos θ ) \rm Y_l^m(\theta, \phi) = \varepsilon \sqrt{\cfrac{2l+1}{4\pi} \cfrac{(l-|m|)!}{(l+|m|)!}} e^{im\phi} P_l^{|m|}(\cos\theta) Ylm(θ,ϕ)=ε4π2l+1(l+∣m∣)!(l−∣m∣)!eimϕPl∣m∣(cosθ)
其中 ε = ( − 1 ) m \rm \varepsilon = (-1)^m ε=(−1)m(当 m > 0 \rm m>0 m>0)或 1 1 1(当 m ≤ 0 \rm m \leq 0 m≤0)。
表:前几个球谐函数
| l \rm l l | m \rm m m | Y l m ( θ , ϕ ) \rm Y_l^m(\theta, \phi) Ylm(θ,ϕ) |
|---|---|---|
| 0 | 0 | 1 4 π \rm \cfrac{1}{\sqrt{4\pi}} 4π1 |
| 1 | 0 | 3 4 π cos θ \rm \sqrt{\cfrac{3}{4\pi}} \cos\theta 4π3cosθ |
| 1 | ±1 | ∓ 3 8 π sin θ e ± i ϕ \rm \mp\sqrt{\cfrac{3}{8\pi}} \sin\theta e^{\pm i\phi} ∓8π3sinθe±iϕ |
| 2 | 0 | 5 16 π ( 3 cos 2 θ − 1 ) \rm \sqrt{\cfrac{5}{16\pi}} (3\cos^2\theta - 1) 16π5(3cos2θ−1) |
4. 完整波函数与量子数
波函数的完整形式为:
ψ n , l , m ( r , θ , ϕ ) = R n , l ( r ) Y l , m ( θ , ϕ ) \rm \psi_{n,l,m}(r, \theta, \phi) = R_{n,l}(r) Y_{l,m}(\theta, \phi) ψn,l,m(r,θ,ϕ)=Rn,l(r)Yl,m(θ,ϕ)
其中 $\rm Y_{l,m}(\theta, \phi) = \Theta_{l,m}(\theta) \Phi_m(\phi) $ 为球谐函数。
5. 量子数的自然出现
通过求解球坐标系下的薛定谔方程,三个量子数自然出现:
- 主量子数 n n n: n = 1 , 2 , 3 , … \rm n = 1, 2, 3, \ldots n=1,2,3,…,决定电子的主要能量水平
- 角量子数 l l l: l = 0 , 1 , 2 , … , n − 1 \rm l = 0, 1, 2, \ldots, n-1 l=0,1,2,…,n−1,决定轨道角动量的大小 L = ℏ l ( l + 1 ) \rm L = \hbar\sqrt{l(l+1)} L=ℏl(l+1)
- 磁量子数 m m m: m = − l , − l + 1 , … , 0 , … , l − 1 , l \rm m = -l, -l+1, \ldots, 0, \ldots, l-1, l m=−l,−l+1,…,0,…,l−1,l,决定角动量在z方向的投影 L z = m ℏ \rm L_z = m\hbar Lz=mℏ
此外,实验结果表明电子还具有**自旋量子数 s s s 和自旋磁量子数 m s m_s ms **,它们无法从薛定谔方程直接得出,需要相对论性量子力学(狄拉克方程)的框架。
表:量子数与原子轨道的关系
| 主量子数 n n n | 角量子数 l l l | 轨道符号 | 磁量子数 m m m的取值 | 轨道数量 | 电子容量 |
|---|---|---|---|---|---|
| 1 | 0 | 1s | 0 | 1 | 2 |
| 2 | 0 | 2s | 0 | 1 | 2 |
| 2 | 1 | 2p | -1, 0, 1 | 3 | 6 |
| 3 | 0 | 3s | 0 | 1 | 2 |
| 3 | 1 | 3p | -1, 0, 1 | 3 | 6 |
| 3 | 2 | 3d | -2, -1, 0, 1, 2 | 5 | 10 |
6. 原子轨道与电子云
6.1 原子轨道的图像表示
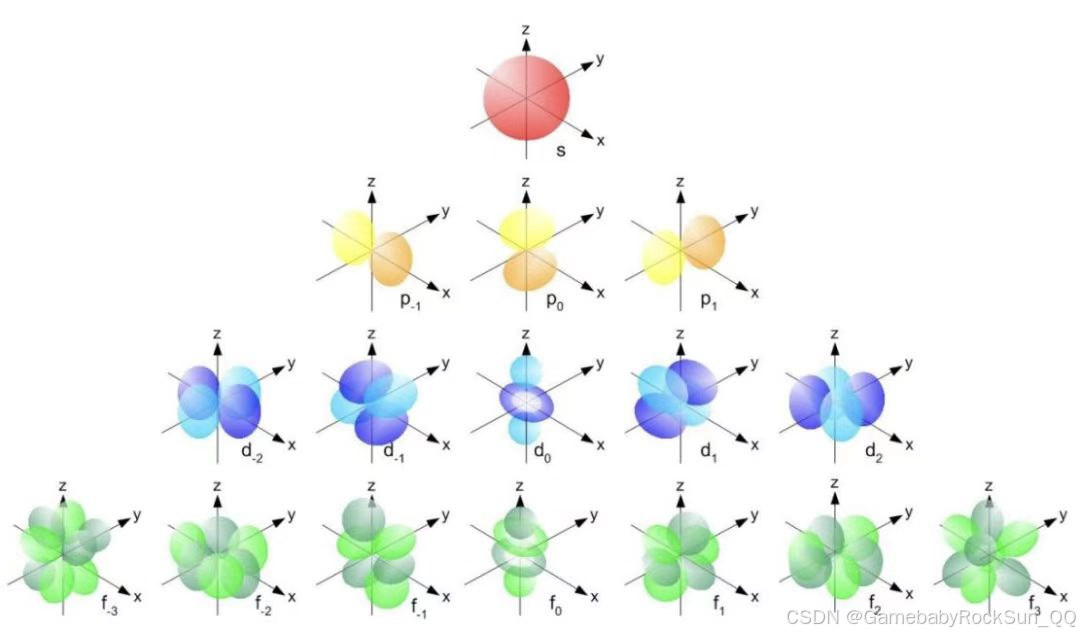
波函数 ψ n l m ( r , θ , ϕ ) = R n l ( r ) Y l m ( θ , ϕ ) \rm \psi_{nlm}(r, \theta, \phi) = R_{nl}(r)Y_l^m(\theta, \phi) ψnlm(r,θ,ϕ)=Rnl(r)Ylm(θ,ϕ) 的绝对值的平方 ∣ ψ ∣ 2 \rm |\psi|^2 ∣ψ∣2 表示电子在空间某点出现的概率密度。为了直观理解原子轨道的形状,通常从两个角度绘制图像:
- 原子轨道的角度分布图:由球谐函数 Y l m ( θ , ϕ ) \rm Y_l^m(\theta, \phi) Ylm(θ,ϕ) 绘制而成,反映波函数在角度方向上的变化
- 原子轨道的径向分布图:由径向波函数 R n l ( r ) \rm R_{nl}(r) Rnl(r) 绘制而成,反映波函数在径向方向上的变化
s轨道( l = 0 l=0 l=0 )呈球形对称;p轨道( l = 1 l=1 l=1 )呈哑铃形,沿坐标轴方向分布;d轨道( l = 2 l=2 l=2 )呈花瓣形,形状更为复杂。
6.2 电子云
电子云是电子概率密度的可视化表示,即 ∣ ψ ∣ 2 |\psi|^2 ∣ψ∣2 在空间各点的值。电子云的角度分布图由 ∣ Y l m ( θ , ϕ ) ∣ 2 |Y_l^m(\theta, \phi)|^2 ∣Ylm(θ,ϕ)∣2 绘制,与原子轨道的角度分布图类似但更"瘦",因为球谐函数的值小于1,平方后值更小。
电子云的径向分布函数 D ( r ) = 4 π r 2 ∣ R n l ( r ) ∣ 2 \rm D(r) = 4\pi r^2 |R_{nl}(r)|^2 D(r)=4πr2∣Rnl(r)∣2 表示在半径 r r r 处的球壳内发现电子的概率,该函数有 n − l n-l n−l 个峰值,对应玻尔理论中的圆形轨道,但量子力学中电子位置是概率性的。
7. 泡利不相容原理的物理内涵
7.1 历史背景与发现过程
泡利不相容原理由奥地利物理学家沃尔夫冈·泡利于1925年提出,最初是为了解释化学元素的周期律和原子光谱的精细结构。20世纪早期,科学家通过化学实验发现,当原子或分子中的电子数为偶数时,系统会表现出更强的化学稳定性。
泡利在总结原子构造时提出:“一个原子中没有任何两个电子可以拥有完全相同的量子态”。这一原理的提出解决了当时原子物理中的多个难题,特别是反常塞曼效应的解释问题。
7.2 基本原理与数学表述
泡利不相容原理的核心内容是:在费米子(自旋为半整数的粒子)组成的系统中,不能有两个或两个以上的粒子处于完全相同的状态。在原子体系中,这一原理表现为:不能有两个或两个以上的电子具有完全相同的四个量子数。
数学表述:
- 波函数反对称性:对于由费米子组成的系统,其总波函数必须是完全反对称的。即如果交换系统中任意两个全同费米子的坐标,波函数会改变符号:
Ψ ( q 1 , q 2 , . . . , q i , . . . , q j , . . . , q N ) = − Ψ ( q 1 , q 2 , . . . , q j , . . . , q i , . . . , q N ) \Psi(q_1, q_2, ..., q_i, ..., q_j, ..., q_N) = -\Psi(q_1, q_2, ..., q_j, ..., q_i, ..., q_N) Ψ(q1,q2,...,qi,...,qj,...,qN)=−Ψ(q1,q2,...,qj,...,qi,...,qN)
其中 q i q_i qi表示第i个粒子的坐标和自旋变量。
- 量子数表述:在原子中,要完全确定一个电子的状态需要四个量子数 ( n , l , m l , m s ) (n, l, m_l, m_s) (n,l,ml,ms),泡利原理要求不可能有两个电子具有完全相同的四个量子数。
7.3 物理意义与深远影响
泡利不相容原理的物理意义极为深远:
-
物质稳定性的基础:如果泡利原理不成立,所有电子都会坍缩到最低能级,原子会塌陷,物质无法保持体积。1967年,弗里曼·戴森与安德鲁·雷纳严格证明了这一点。
-
元素周期律的量子解释:该原理提供了元素周期律的量子力学解释,明确了各电子层最大电子容量为 2 n 2 2n^2 2n2。
-
费米-狄拉克统计的基础:泡利原理是费米-狄拉克统计的基础,决定了金属中的电子行为、白矮星的稳定性等。
-
化学键形成的限制:决定了化学键的性质和分子结构,影响了整个化学学科的发展。
8. 洪特规则的物理内涵
8.1 经验规律与量子解释
洪特规则由德国科学家弗里德里希·洪特于1927年根据大量光谱实验数据总结得出。该规则描述了电子在能量简并的原子轨道(等价轨道)上的排布方式。
洪特规则的主要内容:
- 电子在等价轨道上排布时,总是尽可能分占不同的轨道,且自旋方向相同。
- 等价轨道在全充满( p 6 , d 10 , f 14 p^6, d^{10}, f^{14} p6,d10,f14)、半充满( p 3 , d 5 , f 7 p^3, d^5, f^7 p3,d5,f7)或全空( p 0 , d 0 , f 0 p^0, d^0, f^0 p0,d0,f0)时比较稳定。
8.2 数学表述与能量优化
洪特规则可以从量子力学角度进行解释:
能量优化原则:
- 总自旋S最大时,能量最低:电子间平行自旋减少了它们相遇的概率,从而降低了电子间的静电排斥能。
- 在总自旋S相同的情况下,总轨道角动量L越大,能量越低。
- 在S和L都相同的情况下,对于未满半壳层或刚好半壳层,总角动量J越小能量越低;否则,J越大能量越低。
数学表达式:
洪特规则的能量优化可以表示为体系总哈密顿量的期望值最小化:
⟨ Ψ ∣ H ^ ∣ Ψ ⟩ = E m i n \langle \Psi | \hat{H} | \Psi \rangle = E_{min} ⟨Ψ∣H^∣Ψ⟩=Emin
其中 Ψ \Psi Ψ是满足对称性要求的反对称化波函数。
8.3 物理意义与应用
洪特规则的物理意义主要体现在:
-
电子关联效应:反映了多电子体系中电子之间的关联作用,平行自旋的电子倾向于相互避开,减少库仑排斥。
-
原子光谱解释:成功解释了原子光谱的精细结构,特别是多重线结构的起源。
-
化学性质预测:帮助预测原子和离子的基态电子组态,进而解释其化学性质。
9. 两大原理的协同作用与原子结构
9.1 电子排布三原则的协同
泡利不相容原理、能量最低原理和洪特规则共同构成了原子核外电子排布的基本原则:
- 能量最低原理:电子优先占据能量最低的轨道。
- 泡利不相容原理:每个原子轨道最多容纳两个自旋相反的电子。
- 洪特规则:等价轨道上电子尽可能分占轨道且自旋平行。
9.2 原子核外电子排布实例分析
碳原子(C, Z=6)
碳原子的电子排布式为 1 s 2 2 s 2 2 p 2 1s^2 2s^2 2p^2 1s22s22p2。根据洪特规则,2p轨道上的两个电子不会配对填入同一个轨道,而是分占两个不同的p轨道,且自旋平行:
碳原子:1s² 2s² 2p²↑↓ ↑↓ ↑ ↑2px 2py 2pz
氮原子(N, Z=7)
氮原子的电子排布式为 1 s 2 2 s 2 2 p 3 1s^2 2s^2 2p^3 1s22s22p3。2p轨道上的三个电子分占三个不同的p轨道,且自旋平行,达到半充满稳定结构:
氮原子:1s² 2s² 2p³↑↓ ↑↓ ↑ ↑ ↑2px 2py 2pz
铬原子(Cr, Z=24)的特例
铬的实际电子排布为 [ A r ] 3 d 5 4 s 1 \rm [Ar] 3d^5 4s^1 [Ar]3d54s1,而不是预期的 [ A r ] 3 d 4 4 s 2 \rm [Ar] 3d^4 4s^2 [Ar]3d44s2。这是因为 3 d 5 \rm 3d^5 3d5 半充满结构更加稳定,体现了洪特规则对能量最低原理的补充。
10. 多电子原子体系的薛定谔方程没有精确解
对于多电子原子体系,我们确实无法获得薛定谔方程的解析解,但这并不意味着我们无法通过近似方法或数值计算来高精度地求解它。
下面是导致求解困难的核心原因概览:
| 困难类型 | 核心问题 | 主要影响 |
|---|---|---|
| 多体问题 | 电子-电子之间存在复杂的瞬时相互作用,无法精确分离变量。 | 计算复杂度随电子数增加呈指数级爆炸。 |
| 电子关联 | 电子为躲避彼此而产生复杂的协同运动,基础近似方法会忽略这部分能量。 | 导致能量计算出现显著误差,需要更高级、计算成本极高的方法来修正。 |
| 维度灾难 | 描述体系所需的基函数数量随体系维度(电子数、原子数)增加而指数级增长。 | 即使对于乙烯(C₂H₄)这样的小分子,所需计算资源也已非常庞大。 |
| 反对称性原理 | 电子是费米子,其波函数必须满足泡利不相容原理,数学上要求波函数具有反对称性。 | 最精确的求解方法所需计算项的数量随电子数阶乘(n!)规模增长,仅适用于极小体系。 |
尽管无法获得精确的解析解,科学家们发展出了一系列强大的近似方法和数值技术来求解薛定谔方程,以满足化学、材料和物理等领域的需求。
-
近似计算方法
- 波函数方法:从哈特里-福克(Hartree-Fock)方法出发,逐步考虑电子关联效应,如组态相互作用(CI)、耦合簇(Coupled-Cluster)方法等。这些方法可以系统性地提高精度,但计算成本也急剧增加。
- 密度泛函理论(DFT):这是一种革命性的思路,它不再处理复杂的多电子波函数,而是转而使用电子密度作为基本变量,大大降低了计算难度。DFT是目前计算化学和材料科学中最主流的方法之一,虽然在精度上有所妥协,但在效率和实用性之间取得了很好的平衡。
-
人工智能与神经网络
近年来,人工智能为该领域带来了新的突破。例如,DeepMind开发的费米网络(FermiNet) 和柏林自由大学团队的研究,通过设计专门的深度神经网络来表示波函数,并将泡利不相容原理等物理约束内置其中。这种方法能够以可接受的计算成本,获得前所未有的高精度解,显示出巨大的潜力。国内如张东辉院士团队也在利用AI框架开发高性能的分子势能模型和波函数求解方法。
11. 总结
薛定谔方程在球坐标系下的分离变量法是理解原子结构的数学基础。通过此方法,我们得到了:
- 波函数可分离为径向部分 R ( r ) \rm R(r) R(r) 和角向部分 Y ( θ , ϕ ) \rm Y(\theta, \phi) Y(θ,ϕ) 的乘积
- 角向部分方程的解是球谐函数,自然引入角量子数 l l l和磁量子数 m \rm m m
- 径向方程的解依赖于势能形式,对于库仑势得到主量子数 n n n和能量量子化
- 三个量子数 n , l , m \rm n, l, m n,l,m 完全确定了电子的空间运动状态
- 波函数的图像表示帮助我们直观理解原子轨道和电子概率分布
- 泡利不相容原理和洪特规则是量子力学在原子尺度上的重要体现,它们共同决定了原子的电子结构和元素周期律。泡利原理源于波函数的反对称性要求,而洪特规则则反映了电子关联效应导致的能量优化。这两个原理的协同作用不仅解释了元素的周期性,还为理解化学键形成、物质稳定性等基本问题提供了理论基础。
- 从更深层次看,这两大原理揭示了量子世界与经典世界的根本区别:电子的全同不可区分性、波函数的对称性约束以及量子统计行为,这些都是经典物理学无法理解的现象。正是这些量子规律的发现,使我们能够深入理解微观世界的运行机制,并进而解释宏观世界的多样性和复杂性。
这一理论框架为理解原子核外电子排布、化学键形成和元素周期性提供了坚实的理论基础。
简单来说,薛定谔方程对于除了氢原子以外的绝大多数体系(尤其是多电子分子)都无法获得精确的解析解,这主要是由无法回避的多体问题、电子关联、维度灾难等数学和物理本质困难所决定的。
然而,这并非研究的终点。通过不断发展的近似计算方法和新兴的AI技术,我们能够越来越精确地求解方程,从而深入理解和预测微观世界的性质。
