使用Mathematica对Duffing方程进行非线性分析

        Duffing方程是非线性动力学中描述受迫振动系统的经典模型，其一般形式为：

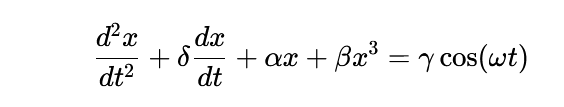
其中δ为阻尼系数，α和β为刚度参数，γ和ω分别为外激励的幅值和频率。非线性恢复力项βx3是Duffing方程的核心，使得系统可呈现​​硬弹簧​​效应（β>0，刚度随位移增大而增强）或​​软弹簧​​效应（β<0，刚度随位移增大而减弱）。

Duffing方程揭示了线性系统无法描述的真实世界复杂性，是理解非线性动力学的重要工具。它可以模拟机械结构（如夹紧梁、弹簧振子）在周期驱动下的非线性振动，尤其在"大变形"或"材料非线性"显著时适用。   

Mathematica中的模型建立与数值求解

在Mathematica中，我们首先定义Duffing方程及其参数：

(* 设置Duffing方程的参数 *)
\[Delta] = 0.3;  (* 阻尼系数 *)
\[Alpha] = -1;  (* 线性刚度系数，负值表示双稳态系统 *)
\[Beta] = 1;    (* 非线性刚度系数 *)
\[Gamma] = 0.5; (* 外力幅值 *)
\[Omega] = 1;   (* 外力频率 *)(* 定义Duffing方程 *)
duffingEq = x''[t] + \[Delta]*x'[t] + \[Alpha]*x[t] + \[Beta]*x[t]^3 == \[Gamma]*Cos[\[Omega]*t];(* 初始条件 *)
initialConditions = {x[0] == 0, x'[0] == 0};

     使用Mathematica的NDSolve进行数值求解，并绘制时间响应和相图：

(* 数值求解Duffing方程 *)
sol = NDSolve[{duffingEq, initialConditions}, x, {t, 0, 5000}, MaxSteps -> Infinity];(* 绘制位移时间响应图 *)
Plot[Evaluate[x[t] /. sol], {t, 0, 50}, PlotRange -> All, AxesLabel -> {"时间 t", "位移 x(t)"}, PlotLabel -> "Duffing方程的时间响应"](* 绘制相图 *)
ParametricPlot[Evaluate[{x[t], x'[t]} /. sol], {t, 10, 100}, PlotRange -> All, AxesLabel -> {"位移 x(t)", "速度 x'(t)"}, PlotLabel -> "Duffing方程的相图"]