动态规划----过河卒
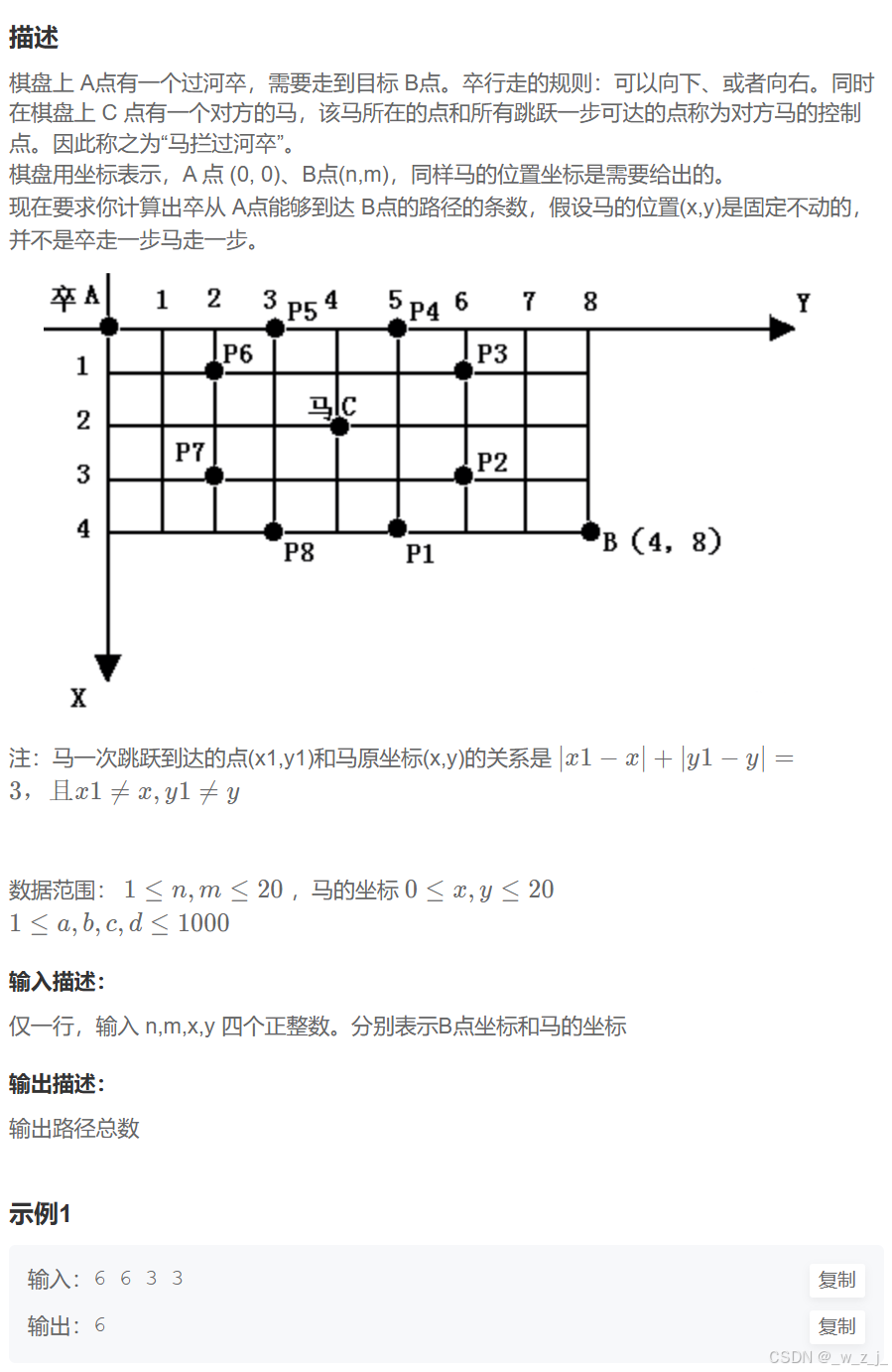
[NOIP2002 普及组] 过河卒_牛客题霸_牛客网
更新:之前的方法很笨,需要控制边界调节,还要自己开辟数组,有一个比较巧的方法,从dp[1][1]开始作为0,0点。人为制造一个虚拟边界。把棋盘整体往右、往下错开一格,从 (1,1) 开始算真正的棋盘,在外面留出一圈安全缓冲区(下标 0 行 / 0 列),所有转移都合法。有以下几点:1.题目说了不会超过20,所以可以提前开一个数组,全局的数组自动初始化为0。2.让dp[0][1]为1,可以使程序根据转移方程自动推导dp[1][1],也就是初始值。初始化情况如下:
j →
0 1 2 3 4
i ↓ ---------------------
0 | 0 1 0 0 0
1 | 0 ? ? ? ?
2 | 0 ? ? ? ?
3 | 0 ? ? ? ?
4 | 0 ? ? ? ?
dp[0][1] = 1这样在更新
dp[1][1]时,dp[1][1] = dp[0][1] + dp[1][0] = 1 + 0 = 1不会访问负下标;
同理,
dp[i][0]默认全为 0(因为数组初始为全 0),自然就能处理“左边界”,同时在处理第一行时,也能处理“上边界”。
#include<iostream>
using namespace std;int n,m,x,y;
long long dp[25][25];int main()
{cin>>n>>m>>x>>y;dp[0][1] = 1;x += 1; y += 1;for(int i = 1;i <= n+1;i++){for(int j = 1;j <= m+1;j++){if(i != x && j != y && abs(i - x) + abs(j - y) == 3|| (i == x && j == y)){dp[i][j] = 0;}else{dp[i][j] = dp[i-1][j] + dp[i][j-1];}}}cout<<dp[n+1][m+1];return 0;
}可以扩展到其它 DP 问题(如路径、网格、棋盘等),方便第一行、第一列的状态转移。
---------------------------------------------------------------------------------------------------------------------------------
有几点需要注意
1.由于我没玩过象棋,所以不知道马走日。其实就是马只能从日的一个对角到另一个对角,横的或者竖的日都可以,其次马可以到的点,是不可以走过去的;
2.虽然题中给的是6,6,但是开数组时要开6+1,6+1,因为数组是这条线,不是棋盘!
假设dp[i][j]为到第i行第j列点的路径总数。初始状态,我们假
dp的第一行和第一列都是1(我一开始是这么想的,后来有错误,但其实应该考虑如果第一行和第一列有马可以到的点的情况)。然后分析状态转移方程,一个点,到他的方向只有左边或者上面,所以到该点的路径数就是从上下来的点和从左过来的点的路径之和:dp[i][j]=dp[i-1][j]+dp[i][j-1]。注意,马可以到到的点的dp直接赋值成0!因为不可到达该点,所以路径为0。
bool is_enemy(int i, int j, int c, int d) {if (i == c && j == d)return true;else if (abs(i - c) + abs(j - d) == 3 && i != c && j != d)return true;elsereturn false;
}int main() {int a, b, c, d;while (cin >> a >> b >> c >> d) { // 注意 while 处理多个 casevector<vector<long long>> dp;vector<long long> v1;for (int i = 0; i < b + 1; i++) {v1.push_back(1);//有问题}dp.push_back(v1);for (int i = 1; i < a + 1; i++) {vector<long long> v(b + 1, 0);v[0]=1;//有问题for (int j = 1; j < b + 1; j++) {if (!is_enemy(i, j, c, d)) {v[j] = dp[i - 1][j] + v[j - 1];} else {v[j] = 0;}}dp.push_back(v);}cout << dp[a][b] << endl;}
}这是我一开始写的,但这里其实是有问题的,就是我开始说的,第一行和第一列应该会有马到的点,这点没有考虑,其次,如果这两个地方有一个点是马到的点的话,它往后的点都不可达,即往后所有点的dp都要为0!!!!!
bool is_enemy(int i, int j, int c, int d) {if (i == c && j == d)return true;else if (abs(i - c) + abs(j - d) == 3 && i != c && j != d)return true;elsereturn false;
}int main() {int a, b, c, d;while (cin >> a >> b >> c >> d) { // 注意 while 处理多个 caseint dealut=1;vector<vector<long long>> dp;vector<long long> v1;for (int i = 0; i < b + 1; i++) {if(is_enemy(0, i, c, d))dealut=0;v1.push_back(dealut);}dp.push_back(v1);int value=1;for (int i = 1; i < a + 1; i++) {vector<long long> v(b + 1, 0);if(is_enemy(i,0,c,d))value=0;v[0]=value;for (int j = 1; j < b + 1; j++) {if (!is_enemy(i, j, c, d)) {v[j] = dp[i - 1][j] + v[j - 1];} else {v[j] = 0;}}dp.push_back(v);}cout << dp[a][b] << endl;}
}再说一句,这里为什么不用int作为dp中值的类型,因为有一个测试例子,路径数达到了56477364570,int为 −2,147,483,648∼2,147,483,647,放不下,所以这里要用longlong类型。
