当前位置：首页 > news >正文

逻辑方阵（Logical Square）解说

news 2025/10/18 13:43:52

逻辑方阵（Logical Square）解说

传统的逻辑方阵是波爱修斯（约公元5-6世纪）在注释和传播亚里士多德（公元前4世纪）《工具论》中逻辑思想的过程中，首次用图表的形式清晰地展示了这四种命题之间的关系。这个图表就是后世所称的“逻辑方阵”或“对当关系方阵”。

传统的逻辑方阵是逻辑学发展史上的一个里程碑，是传统形式逻辑的 “浓缩精华”，其价值体现在 “奠定形式推理的基础” 和 “简化推理判断” 两方面，至今仍是逻辑入门的重要工具。

逻辑方阵（又称“对当方阵”、“逻辑正方形”）是传统词项逻辑里的一张“四格真值关系图：

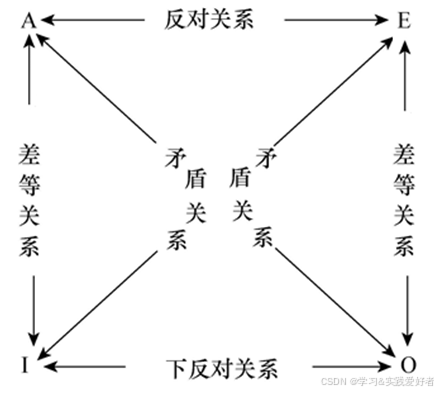
对当口诀：

上不同真——反对关系、下不同假——下反对关系、对角必反——矛盾关系、上真下必真，下假上必假——差等关系。

下面解析之。

逻辑方阵的核心是 4 种结构固定的直言命题，它们都以 “主项（S，指被判断的对象）” 和 “谓项（P，指对象的属性）” 为核心，通过 “量项（全称：所有 / 特称：有的）” 和 “联项（肯定：是 / 否定：不是）” 组合而成，具体分类如下：

命题类型	简称	逻辑形式	含义（以 “S = 学生，P = 及格” 为例）	量（全称 / 特称）	质（肯定 / 否定）
全称肯定命题	A	所有 S 是 P	所有学生都及格	全称	肯定
全称否定命题	E	所有 S 不是 P	所有学生都不及格	全称	否定
特称肯定命题	I	有的 S 是 P	有的学生及格	特称	肯定
特称否定命题	O	有的 S 不是 P	有的学生不及格	特称	否定

说明：

1．A-E-I-O 是从拉丁动词affirmo（我肯定） / nego（我否定），取AffIrmo / nEgO元音 A-I-E-O之助记符号。

2. 传统逻辑中 “有的” 表示 “至少有一个”（存在即可，不排除 “全部”），与日常语言中 “有的 = 部分” 的含义不同。

在逻辑方阵中，四种命题之间存在四种基本的真假制约关系

1. 矛盾关系（A 与 O、E 与 I：“非此即彼，必一真一假”）

核心规则：不能同真，不能同假 —— 只要一个为真，另一个必为假；只要一个为假，另一个必为真（无中间状态）。
示例验证：
- A（所有学生及格）与 O（有的学生不及格）：若 A 为真（全及格），则 O 必为假（不可能有不及格）；若 A 为假（不是全及格），则 O 必为真（一定有不及格）。
- E（所有学生不及格）与 I（有的学生及格）：若 E 为真（全不及格），则 I 必为假（不可能有及格）；若 E 为假（不是全不及格），则 I 必为真（一定有及格）。
本质：两种命题是 “完全对立的矛盾面”，覆盖了所有可能情况且无重叠，因此真假严格互斥。

2. 反对关系（A 与 E：“不能同真，可同假”）

核心规则：不能同时为真，但可以同时为假 —— 一个为真，另一个必为假；一个为假，另一个 “真假不定”（可能真，也可能假）。
示例验证：
- A（所有学生及格）与 E（所有学生不及格）：若 A 为真（全及格），则 E 必为假（不可能全不及格）；若 A 为假（不是全及格），E 可能为真（全不及格），也可能为假（部分及格、部分不及格）—— 此时 A 和 E 同时为假。
本质：两种命题是 “大范围的对立”（全称肯定 vs 全称否定），但未覆盖所有可能（中间有 “部分及格” 的情况），因此只能排除 “同真”，无法排除 “同假”。

3. 下反对关系（I 与 O：“不能同假，可同真”）

核心规则：不能同时为假，但可以同时为真 —— 一个为假，另一个必为真；一个为真，另一个 “真假不定”（可能真，也可能假）。
示例验证：
- I（有的学生及格）与 O（有的学生不及格）：若 I 为假（没有学生及格 = 全不及格），则 O 必为真（一定有不及格）；若 I 为真（有及格的），O 可能为真（部分及格、部分不及格），也可能为假（全及格）—— 此时 I 和 O 同时为真。
本质：两种命题是 “小范围的补充”（特称肯定 vs 特称否定），覆盖了所有可能（若 “有的及格” 为假，必是 “全不及格”，则 “有的不及格” 为真），但存在重叠（部分及格、部分不及格时两者同真），因此只能排除 “同假”，无法排除 “同真”。

4. 差等关系（A 与 I、E 与 O：“全称与特称的从属，真假有传递性”）

核心规则：全称命题的真假 “能传递” 给特称命题，特称命题的真假 “不能反向传递” 给全称命题，可总结为两句话：

① 全称真→特称真；特称假→全称假（“上真下必真，下假上必假”）；

② 全称假→特称真假不定；特称真→全称真假不定（“上假下不定，下真上不定”）。

示例验证（A 与 I）：
- 若 A（所有学生及格）为真→I（有的学生及格）必为真（“全及格” 必然包含 “部分及格”）；
- 若 I（有的学生及格）为假→A（所有学生及格）必为假（“没有及格的” 不可能是 “全及格”）；
- 若 A（所有学生及格）为假→I（有的学生及格）真假不定（A 假可能是 “部分及格”，此时 I 真；也可能是 “全不及格”，此时 I 假）；
- 若 I（有的学生及格）为真→A（所有学生及格）真假不定（I 真可能是 “全及格”，此时 A 真；也可能是 “部分及格”，此时 A 假）。
示例验证（E 与 O）：同理，E（所有学生不及格）为真→O（有的学生不及格）必为真；O 为假→E 必为假；E 假→O 不定；O 真→E 不定。

本质：特称命题是 “全称命题的子集”—— 全称命题成立，子集必然成立；子集不成立，全称必然不成立；但子集成立，全称不一定成立（子集可能只是部分）；全称不成立，子集也不一定不成立（可能只是另一部分不成立），例如 A（所有学生及格）为假（全称不成立），可能是“部分学生及格、部分不及格”（此时 I（有的学生及格）为真，子集成立），也可能是“所有学生不及格”（此时 I 为假，子集不成立）。

总结对比表格：

关系类型	适用命题对	能否同真	能否同假	核心推断规则
反对关系	A-E	不能	能	一方真→另一方假，一方假→另一方不定
下反对关系	I-O	能	不能	一方假→另一方真，一方真→另一方不定
矛盾关系	A-O、E-I	不能	不能	必有一真一假，一方真→另一方假，一方假→另一方真
差等关系	A-I、E-O	能（全称真时）	能（全称假时）	全称真→特称真，特称假→全称假，其余情况不定