当前位置： 首页 > news >正文

机器学习入门，无监督学习之DBSCAN聚类算法完全指南：面向Java开发者的Python实现详解

news 2025/10/16 16:34:48

机器学习入门：无监督学习之DBSCAN聚类算法完全指南

面向Java开发者的Python实现详解

一、DBSCAN算法核心概念

1.1 什么是DBSCAN？

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，与K-Means相比具有独特优势：

  • ✅ 不需要预先指定簇的数量
  • ✅ 可以发现任意形状的簇
  • ✅ 能够自动识别噪声点（异常值）
  • ✅ 对异常值不敏感

1.2 核心概念（Java开发者视角）

DBSCAN概念Java类比通俗解释
核心点社交网络中的"中心人物"周围有很多邻居的点
边界点“普通成员”在核心点附近，但自己朋友不多
噪声点“独行侠”周围没什么朋友，也不在任何核心点附近
ε-邻域“社交距离半径”判断是否为朋友的临界距离
最小样本数“最小朋友圈规模”成为核心人物需要的最少朋友数

二、DBSCAN算法原理详解

2.1 算法核心思想

DBSCAN基于一个简单而强大的思想：一个簇是由密度相连的点的最大集合组成。

2.2 算法步骤

// Java风格算法伪代码
public class DBSCAN {public List<Cluster> cluster(Point[] points, double eps, int minPts) {List<Cluster> clusters = new ArrayList<>();boolean[] visited = new boolean[points.length];int clusterId = 0;for (int i = 0; i < points.length; i++) {if (!visited[i]) {visited[i] = true;List<Point> neighbors = findNeighbors(points, i, eps);if (neighbors.size() >= minPts) {// 创建新簇Cluster cluster = new Cluster(++clusterId);expandCluster(points, i, neighbors, cluster, visited, eps, minPts);clusters.add(cluster);} else {// 标记为噪声points[i].setClusterId(-1);}}}return clusters;}
}

2.3 关键定义

  1. ε-邻域：以点p为中心，半径为ε的圆形区域
  2. 核心点：ε-邻域内至少包含min_samples个点
  3. 直接密度可达：点q在点p的ε-邻域内，且p是核心点
  4. 密度可达：存在一条密度相连的路径
  5. 密度相连：存在一个核心点o，使p和q都从o密度可达

三、完整Python代码实现

3.1 环境准备和导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons, make_blobs
from sklearn.preprocessing import StandardScaler
from collections import deque
import warnings
warnings.filterwarnings('ignore')# Python库说明（Java开发者参考）：
# numpy：数值计算库，类似Java的Arrays + Math组合
# matplotlib：绘图库，类似Java的JFreeChart
# sklearn：机器学习库，类似Java的Weka
# deque：双端队列，类似Java的LinkedList

3.2 自定义DBSCAN实现

class CustomDBSCAN:"""自定义DBSCAN实现相当于Java类：public class CustomDBSCAN { ... }"""def __init__(self, eps=0.5, min_samples=5):"""构造函数:param eps: ε半径，相当于Java的double eps:param min_samples: 最小样本数，相当于Java的int minSamples"""self.eps = epsself.min_samples = min_samplesself.labels_ = None  # 聚类结果标签def fit_predict(self, X):"""训练模型并返回聚类标签:param X: 输入数据，形状(n_samples, n_features):return: 标签数组，-1表示噪声点Java等价方法：public int[] fitPredict(double[][] X) { ... }"""n_samples = X.shape[0]  # 样本数量，相当于Java的X.length# 初始化标签数组，所有点标记为未分类(-1)# np.full 相当于Java的Arrays.fill(labels, -1)labels = np.full(n_samples, -1)# 访问标记数组，避免重复处理# 相当于Java的boolean[] visited = new boolean[n_samples]visited = np.zeros(n_samples, dtype=bool)cluster_id = 0  # 簇ID计数器# 遍历所有数据点for i in range(n_samples):if not visited[i]:visited[i] = True  # 标记为已访问# 找到当前点的ε-邻域邻居neighbors = self._find_neighbors(X, i)if len(neighbors) < self.min_samples:# 邻居数量不足，标记为噪声点labels[i] = -1else:# 发现新簇cluster_id += 1labels[i] = cluster_id# 使用队列扩展簇（广度优先搜索）# deque 相当于Java的Queue<Integer> queue = new LinkedList<>()queue = deque(neighbors)while queue:# 取出队列中的下一个点j = queue.popleft()  # 相当于Java的queue.poll()if not visited[j]:visited[j] = True# 找到j点的邻居j_neighbors = self._find_neighbors(X, j)if len(j_neighbors) >= self.min_samples:# j也是核心点，将其邻居加入队列# 使用集合操作避免重复添加new_neighbors = set(j_neighbors) - set(queue)queue.extend(new_neighbors)# 如果j点还没有被分配到任何簇，分配到当前簇if labels[j] == -1:labels[j] = cluster_idself.labels_ = labelsreturn labelsdef _find_neighbors(self, X, point_index):"""找到指定点的ε-邻域内的所有邻居:param X: 数据集:param point_index: 目标点索引:return: 邻居索引列表Java等价方法：private List<Integer> findNeighbors(double[][] X, int pointIndex) { ... }"""# 计算目标点到所有其他点的欧氏距离# 这里使用了NumPy的广播机制，避免显式循环# 相当于Java中的向量化计算distances = np.sqrt(np.sum((X - X[point_index])**2, axis=1))# 找到距离小于等于eps的所有点neighbors = np.where(distances <= self.eps)[0]return neighbors.tolist()  # 转换为Python列表

3.3 数据生成和工具函数

def generate_sample_data():"""生成示例数据集，包含不同形状的簇和噪声返回标准化后的数据Java等价方法：public double[][] generateSampleData() { ... }"""# 生成半月形数据（非凸形状）# 相当于：创建两个半月形分布的点集X1, _ = make_moons(n_samples=300, noise=0.1, random_state=42)# 生成球形数据（凸形状）X2, _ = make_blobs(n_samples=100, centers=1, cluster_std=0.1, random_state=42)X2 = X2 + [2.5, 0]  # 平移第二组数据# 添加一些随机噪声点# 相当于：在数据空间中随机撒点noise = np.random.uniform(-2, 2, (50, 2))# 合并所有数据# np.vstack 相当于Java中的数组合并X = np.vstack([X1, X2, noise])# 数据标准化（重要：DBSCAN对数据尺度敏感）# 相当于Java中的：(value - mean) / stdscaler = StandardScaler()X_scaled = scaler.fit_transform(X)return X_scaleddef plot_clustering_results(X, labels, title, algorithm_name):"""可视化聚类结果:param X: 数据点:param labels: 聚类标签:param title: 图表标题:param algorithm_name: 算法名称Java等价方法：public void plotClusteringResults(double[][] X, int[] labels, String title) { ... }"""plt.figure(figsize=(12, 5))# 子图1：聚类结果plt.subplot(1, 2, 1)# 获取唯一的簇标签unique_labels = set(labels)# 为每个簇分配颜色colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]for k, col in zip(unique_labels, colors):if k == -1:# 噪声点用黑色显示col = [0, 0, 0, 1]  # RGBA颜色：黑色# 创建布尔掩码选择当前簇的点# 相当于Java中的条件筛选class_member_mask = (labels == k)# 提取当前簇的点xy = X[class_member_mask]# 绘制这些点plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),   # 填充颜色markeredgecolor='k',          # 边框颜色markersize=8 if k != -1 else 6,  # 点大小label=f'Cluster {k}' if k != -1 else 'Noise')plt.title(f'{title}\n{algorithm_name}')plt.xlabel('Feature 1 (标准化)')plt.ylabel('Feature 2 (标准化)')plt.legend()plt.grid(True, alpha=0.3)# 子图2：统计信息plt.subplot(1, 2, 2)# 统计簇信息cluster_info = {}for label in labels:if label not in cluster_info:cluster_info[label] = 0cluster_info[label] += 1# 准备柱状图数据clusters = []counts = []colors_bar = []for label, count in cluster_info.items():clusters.append(f'Cluster {label}' if label != -1 else 'Noise')counts.append(count)if label == -1:colors_bar.append('black')else:idx = list(unique_labels).index(label)colors_bar.append(plt.cm.Spectral(idx / len(unique_labels)))# 绘制柱状图bars = plt.bar(clusters, counts, color=colors_bar, alpha=0.7)plt.title('簇大小分布')plt.xlabel('簇标签')plt.ylabel('点数')plt.xticks(rotation=45)# 在柱子上添加数值标签for bar in bars:height = bar.get_height()plt.text(bar.get_x() + bar.get_width()/2., height,f'{int(height)}', ha='center', va='bottom')plt.tight_layout()plt.show()def analyze_parameters(X):"""分析DBSCAN参数敏感性:param X: 数据集Java等价方法：public void analyzeParameters(double[][] X) { ... }"""print("=== DBSCAN参数敏感性分析 ===")# 测试不同的参数组合eps_values = [0.2, 0.3, 0.4, 0.5]min_samples_values = [3, 5, 10]fig, axes = plt.subplots(len(eps_values), len(min_samples_values), figsize=(18, 15))for i, eps in enumerate(eps_values):for j, min_samples in enumerate(min_samples_values):# 创建DBSCAN实例dbscan = CustomDBSCAN(eps=eps, min_samples=min_samples)labels = dbscan.fit_predict(X)ax = axes[i, j]# 统计结果n_clusters = len(set(labels)) - (1 if -1 in labels else 0)n_noise = list(labels).count(-1)# 绘制聚类结果unique_labels = set(labels)colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]for k, col in zip(unique_labels, colors):if k == -1:col = [0, 0, 0, 1]class_member_mask = (labels == k)xy = X[class_member_mask]ax.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=4)ax.set_title(f'eps={eps}, min_samples={min_samples}\n'f'Clusters: {n_clusters}, Noise: {n_noise}', fontsize=10)ax.grid(True, alpha=0.3)plt.tight_layout()plt.show()

3.4 主演示函数

def main_demo():"""主演示函数：展示DBSCAN的完整工作流程Java等价方法：public static void main(String[] args) { ... }"""print("=" * 60)print("DBSCAN聚类算法完整演示")print("=" * 60)# 1. 数据生成print("\n1. 生成示例数据...")X = generate_sample_data()print(f"数据集形状: {X.shape} (样本数 × 特征数)")print(f"前5个样本点:\n{X[:5]}")# 2. 自定义DBSCAN演示print("\n2. 使用自定义DBSCAN实现...")custom_dbscan = CustomDBSCAN(eps=0.3, min_samples=5)custom_labels = custom_dbscan.fit_predict(X)# 统计结果n_clusters_custom = len(set(custom_labels)) - (1 if -1 in custom_labels else 0)n_noise_custom = list(custom_labels).count(-1)print(f"自定义DBSCAN结果:")print(f"  - 发现簇数量: {n_clusters_custom}")print(f"  - 噪声点数量: {n_noise_custom}")print(f"  - 聚类标签分布: {np.unique(custom_labels, return_counts=True)}")# 可视化自定义DBSCAN结果plot_clustering_results(X, custom_labels, "自定义实现", "Custom DBSCAN")# 3. 与sklearn官方实现对比print("\n3. 与sklearn官方实现对比...")from sklearn.cluster import DBSCANsklearn_dbscan = DBSCAN(eps=0.3, min_samples=5)sklearn_labels = sklearn_dbscan.fit_predict(X)n_clusters_sklearn = len(set(sklearn_labels)) - (1 if -1 in sklearn_labels else 0)n_noise_sklearn = list(sklearn_labels).count(-1)print(f"Sklearn DBSCAN结果:")print(f"  - 发现簇数量: {n_clusters_sklearn}")print(f"  - 噪声点数量: {n_noise_sklearn}")print(f"  - 聚类标签分布: {np.unique(sklearn_labels, return_counts=True)}")# 可视化sklearn结果plot_clustering_results(X, sklearn_labels, "官方库实现", "Sklearn DBSCAN")# 4. 算法性能比较print("\n4. 算法性能比较...")# 计算轮廓系数（聚类质量指标，-1到1，越大越好）from sklearn.metrics import silhouette_scoreif n_clusters_custom > 1:  # 轮廓系数需要至少2个簇custom_score = silhouette_score(X, custom_labels)sklearn_score = silhouette_score(X, sklearn_labels)print(f"轮廓系数比较:")print(f"  - 自定义DBSCAN: {custom_score:.4f}")print(f"  - Sklearn DBSCAN: {sklearn_score:.4f}")else:print("轮廓系数需要至少2个非噪声簇才能计算")# 5. 参数敏感性分析print("\n5. 进行参数敏感性分析...")analyze_parameters(X)# 6. 实用建议print("\n6. DBSCAN使用建议:")print("   ✅ eps选择: 使用k-距离图找到拐点")print("   ✅ min_samples: 从维度+1开始尝试")print("   ✅ 数据预处理: 必须进行标准化")print("   ✅ 噪声处理: 噪声点可用于异常检测")print("   ✅ 适用场景: 任意形状簇、有噪声数据")return X, custom_labels, sklearn_labels# 运行主程序
if __name__ == "__main__":# 执行演示X, custom_labels, sklearn_labels = main_demo()print("\n" + "=" * 60)print("演示完成！")print("=" * 60)

四、Python语法详细解释（针对Java开发者）

4.1 关键Python语法对比

# ==================== 类定义 ====================
# Python
class CustomDBSCAN:def __init__(self, eps=0.5, min_samples=5):self.eps = epsself.min_samples = min_samples# Java等价代码
"""
public class CustomDBSCAN {private double eps;private int minSamples;public CustomDBSCAN(double eps, int minSamples) {this.eps = eps;this.minSamples = minSamples;}
}
"""# ==================== 数组操作 ====================
# Python (NumPy)
labels = np.full(n_samples, -1)
distances = np.sqrt(np.sum((X - X[point_index])**2, axis=1))# Java等价代码
"""
int[] labels = new int[nSamples];
Arrays.fill(labels, -1);double[] distances = new double[nSamples];
for (int i = 0; i < nSamples; i++) {double sum = 0.0;for (int j = 0; j < nFeatures; j++) {double diff = X[i][j] - X[pointIndex][j];sum += diff * diff;}distances[i] = Math.sqrt(sum);
}
"""# ==================== 布尔索引 ====================
# Python
class_member_mask = (labels == k)
xy = X[class_member_mask]# Java等价代码
"""
List<double[]> xy = new ArrayList<>();
for (int i = 0; i < labels.length; i++) {if (labels[i] == k) {xy.add(X[i]);}
}
"""# ==================== 集合操作 ====================
# Python
new_neighbors = set(j_neighbors) - set(queue)
queue.extend(new_neighbors)# Java等价代码
"""
Set<Integer> jNeighborsSet = new HashSet<>(jNeighbors);
Set<Integer> queueSet = new HashSet<>(queue);
jNeighborsSet.removeAll(queueSet);
queue.addAll(jNeighborsSet);
"""

4.2 NumPy广播机制

# Python向量化计算（高效）
distances = np.sqrt(np.sum((X - X[point_index])**2, axis=1))# 等价的手动循环（低效，但容易理解）
distances_manual = []
for i in range(len(X)):distance = 0.0for j in range(len(X[i])):distance += (X[i][j] - X[point_index][j]) ** 2distances_manual.append(np.sqrt(distance))

五、DBSCAN实战指南

5.1 参数选择策略

ε (eps) 选择方法：
def find_optimal_eps(X, k=4):"""使用k-距离图找到最优eps:param X: 数据集:param k: 最近邻数量（通常取min_samples-1）"""from sklearn.neighbors import NearestNeighbors# 计算每个点到第k个最近邻的距离neighbors = NearestNeighbors(n_neighbors=k)neighbors_fit = neighbors.fit(X)distances, indices = neighbors_fit.kneighbors(X)# 按距离排序k_distances = np.sort(distances[:, k-1], axis=0)# 绘制k-距离图plt.figure(figsize=(10, 6))plt.plot(k_distances)plt.xlabel('Points sorted by distance')plt.ylabel(f'{k}-th nearest neighbor distance')plt.title('K-Distance Graph for EPS selection')plt.grid(True, alpha=0.3)plt.show()# 寻找"拐点"（曲率最大的点）return k_distances# 使用示例
# optimal_eps = find_optimal_eps(X, k=4)
min_samples 经验法则：
  • 最小值：min_samples ≥ 数据维度 + 1
  • 常用值：2 × 数据维度
  • 大数据集：适当增大min_samples减少噪声

5.2 与K-Means对比

特性DBSCANK-Means
簇形状任意形状只能发现球形簇
噪声处理✅ 自动识别噪声点❌ 对噪声敏感
簇数量✅ 自动确定❌ 需要预先指定
初始化✅ 不敏感❌ 对初始值敏感
复杂度O(n log n)O(n)
数据分布假设基于密度基于距离和方差

5.3 实际应用场景

场景1：客户细分
# 使用DBSCAN进行客户行为分析
def customer_segmentation(customer_data):"""基于客户行为数据进行细分"""# 1. 数据预处理scaler = StandardScaler()scaled_data = scaler.fit_transform(customer_data)# 2. 参数调优eps = 0.5  # 通过k-距离图确定min_samples = 10  # 根据业务理解调整# 3. 聚类分析dbscan = DBSCAN(eps=eps, min_samples=min_samples)segments = dbscan.fit_predict(scaled_data)return segments
场景2：异常检测
def detect_anomalies(transaction_data):"""使用DBSCAN检测异常交易"""dbscan = DBSCAN(eps=0.3, min_samples=5)labels = dbscan.fit_predict(transaction_data)# 噪声点即为异常点anomalies = transaction_data[labels == -1]return anomalies, labels

六、总结

6.1 核心要点

  1. DBSCAN优势：

    • 不需要预设簇数量
    • 能发现任意形状的簇
    • 对噪声鲁棒
    • 结果可解释性强

  2. 关键参数：

    • eps：邻域半径，决定簇的紧密程度
    • min_samples：核心点所需的最小邻居数

  3. 适用场景：

    • 数据分布未知或非球形
    • 需要自动识别异常值
    • 簇的数量和形状不确定

6.2 下一步学习建议

  1. 进阶主题：

    • HDBSCAN（层次DBSCAN）
    • OPTICS（改进的DBSCAN）
    • 聚类评估指标

  2. 实践项目：

    • 电商用户行为聚类
    • 网络入侵检测
    • 图像分割应用

  3. 相关算法：

    • 高斯混合模型（GMM）
    • 层次聚类
    • 谱聚类

通过本指南，你不仅掌握了DBSCAN算法的原理和实现，还了解了如何在Python中应用它解决实际问题。作为Java开发者，理解Python的向量化操作和科学计算库的使用，将为你在数据科学领域打开新的大门。

记住：理论理解 + 实践编码 = 真正掌握！

附：聚类效果

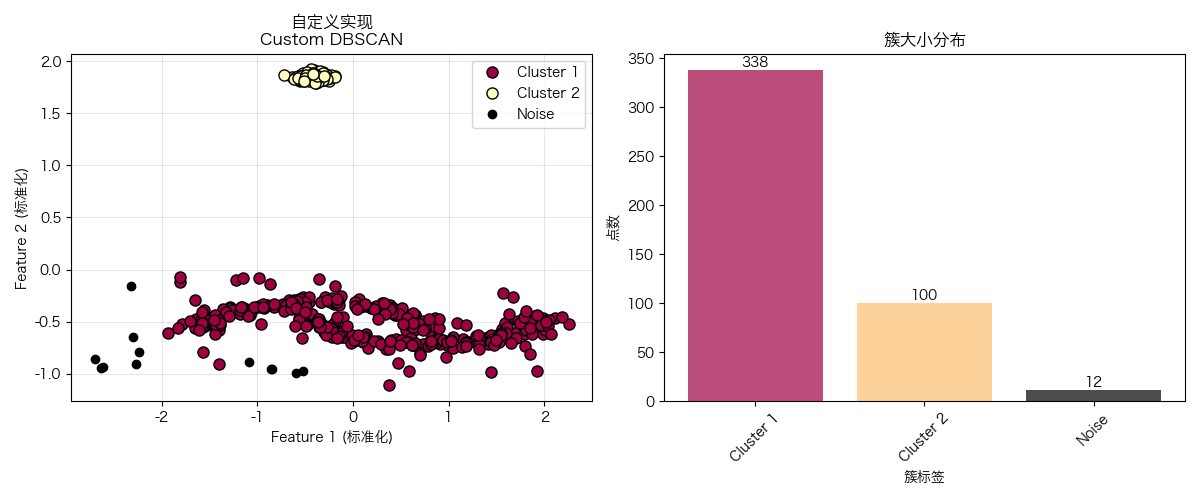
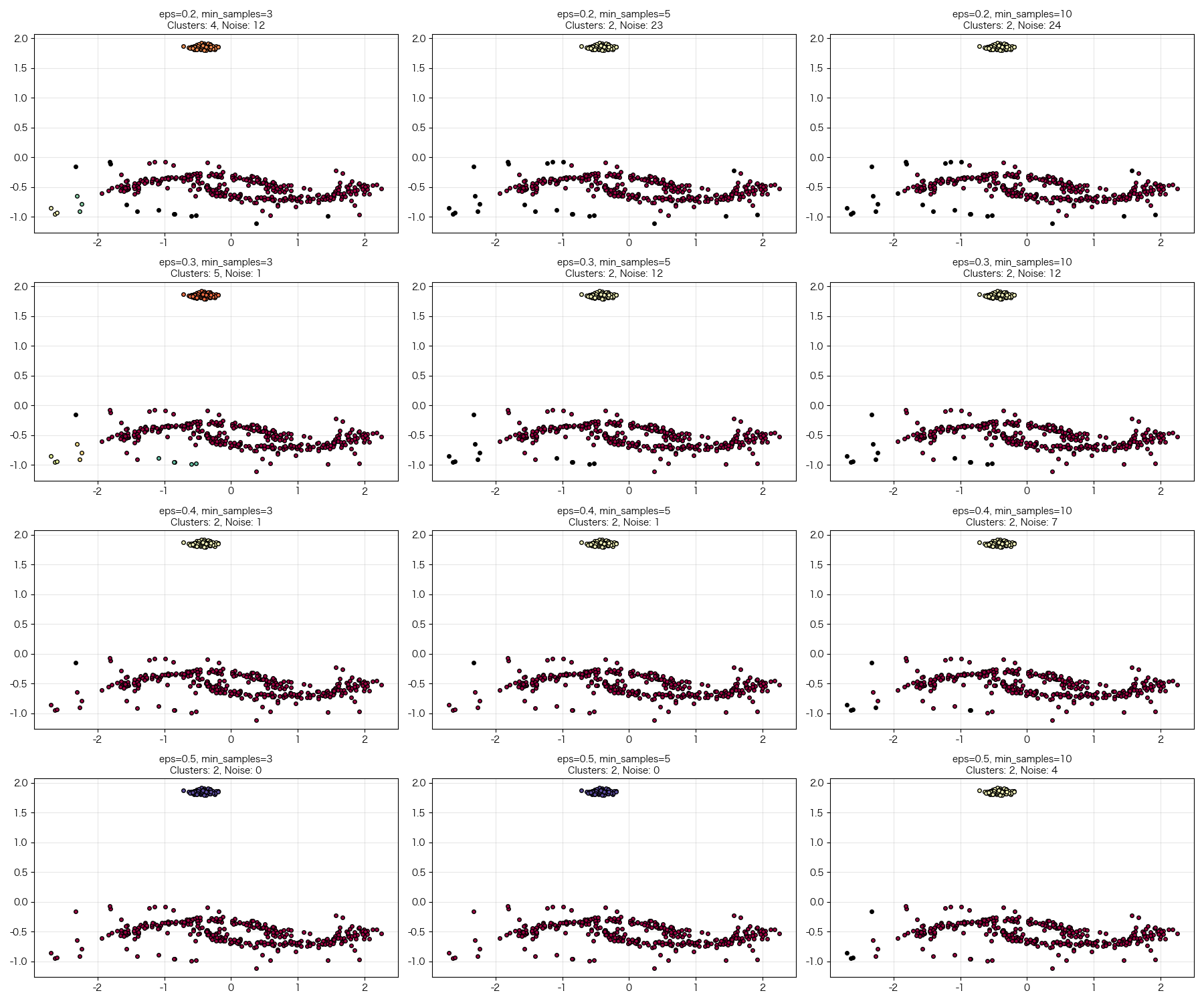
在这里插入图片描述
在这里插入图片描述

附：python源码

# -*- coding: utf-8 -*-
"""
DBSCAN聚类算法完整实现
面向Java开发者的Python代码详解
"""import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons, make_blobs
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN as SklearnDBSCAN
from sklearn.metrics import silhouette_score
from collections import deque
import warningswarnings.filterwarnings('ignore')class CustomDBSCAN:"""自定义DBSCAN实现相当于Java类：public class CustomDBSCAN { ... }"""def __init__(self, eps=0.5, min_samples=5):"""构造函数:param eps: ε半径，相当于Java的double eps:param min_samples: 最小样本数，相当于Java的int minSamples"""self.eps = epsself.min_samples = min_samplesself.labels_ = None  # 聚类结果标签def fit_predict(self, X):"""训练模型并返回聚类标签:param X: 输入数据，形状(n_samples, n_features):return: 标签数组，-1表示噪声点"""n_samples = X.shape[0]  # 样本数量，相当于Java的X.length# 初始化标签数组，所有点标记为未分类(-1)labels = np.full(n_samples, -1)# 访问标记数组，避免重复处理visited = np.zeros(n_samples, dtype=bool)cluster_id = 0  # 簇ID计数器# 遍历所有数据点for i in range(n_samples):if not visited[i]:visited[i] = True  # 标记为已访问# 找到当前点的ε-邻域邻居neighbors = self._find_neighbors(X, i)if len(neighbors) < self.min_samples:# 邻居数量不足，标记为噪声点labels[i] = -1else:# 发现新簇cluster_id += 1labels[i] = cluster_id# 使用队列扩展簇（广度优先搜索）queue = deque(neighbors)while queue:# 取出队列中的下一个点j = queue.popleft()if not visited[j]:visited[j] = True# 找到j点的邻居j_neighbors = self._find_neighbors(X, j)if len(j_neighbors) >= self.min_samples:# j也是核心点，将其邻居加入队列# 使用集合操作避免重复添加new_neighbors = set(j_neighbors) - set(queue)queue.extend(new_neighbors)# 如果j点还没有被分配到任何簇，分配到当前簇if labels[j] == -1:labels[j] = cluster_idself.labels_ = labelsreturn labelsdef _find_neighbors(self, X, point_index):"""找到指定点的ε-邻域内的所有邻居:param X: 数据集:param point_index: 目标点索引:return: 邻居索引列表"""# 计算目标点到所有其他点的欧氏距离distances = np.sqrt(np.sum((X - X[point_index]) ** 2, axis=1))# 找到距离小于等于eps的所有点neighbors = np.where(distances <= self.eps)[0]return neighbors.tolist()def generate_sample_data():"""生成示例数据集，包含不同形状的簇和噪声返回标准化后的数据"""# 生成半月形数据（非凸形状）X1, _ = make_moons(n_samples=300, noise=0.1, random_state=42)# 生成球形数据（凸形状）X2, _ = make_blobs(n_samples=100, centers=1, cluster_std=0.1, random_state=42)X2 = X2 + [2.5, 0]  # 平移第二组数据# 添加一些随机噪声点noise = np.random.uniform(-2, 2, (50, 2))# 合并所有数据X = np.vstack([X1, X2, noise])# 数据标准化（重要：DBSCAN对数据尺度敏感）scaler = StandardScaler()X_scaled = scaler.fit_transform(X)return X_scaleddef plot_clustering_results(X, labels, title, algorithm_name):"""可视化聚类结果:param X: 数据点:param labels: 聚类标签:param title: 图表标题:param algorithm_name: 算法名称"""plt.rcParams['font.sans-serif'] = ['Hiragino Sans GB']  # 指定默认字体为黑体plt.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示为方块的问题plt.figure(figsize=(12, 5))# 子图1：聚类结果plt.subplot(1, 2, 1)# 获取唯一的簇标签unique_labels = set(labels)# 为每个簇分配颜色colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]for k, col in zip(unique_labels, colors):if k == -1:# 噪声点用黑色显示col = [0, 0, 0, 1]  # RGBA颜色：黑色# 创建布尔掩码选择当前簇的点class_member_mask = (labels == k)# 提取当前簇的点xy = X[class_member_mask]# 绘制这些点plt.plot(xy[:, 0], xy[:, 1], 'o',markerfacecolor=tuple(col),markeredgecolor='k',markersize=8 if k != -1 else 6,label=f'Cluster {k}' if k != -1 else 'Noise')plt.title(f'{title}\n{algorithm_name}')plt.xlabel('Feature 1 (标准化)')plt.ylabel('Feature 2 (标准化)')plt.legend()plt.grid(True, alpha=0.3)# 子图2：统计信息plt.subplot(1, 2, 2)# 统计簇信息cluster_info = {}for label in labels:if label not in cluster_info:cluster_info[label] = 0cluster_info[label] += 1# 准备柱状图数据clusters = []counts = []colors_bar = []for label, count in cluster_info.items():clusters.append(f'Cluster {label}' if label != -1 else 'Noise')counts.append(count)if label == -1:colors_bar.append('black')else:idx = list(unique_labels).index(label)colors_bar.append(plt.cm.Spectral(idx / len(unique_labels)))# 绘制柱状图bars = plt.bar(clusters, counts, color=colors_bar, alpha=0.7)plt.title('簇大小分布')plt.xlabel('簇标签')plt.ylabel('点数')plt.xticks(rotation=45)# 在柱子上添加数值标签for bar in bars:height = bar.get_height()plt.text(bar.get_x() + bar.get_width() / 2., height,f'{int(height)}', ha='center', va='bottom')plt.tight_layout()plt.show()def analyze_parameters(X):"""分析DBSCAN参数敏感性:param X: 数据集"""print("=== DBSCAN参数敏感性分析 ===")# 测试不同的参数组合eps_values = [0.2, 0.3, 0.4, 0.5]min_samples_values = [3, 5, 10]fig, axes = plt.subplots(len(eps_values), len(min_samples_values),figsize=(18, 15))for i, eps in enumerate(eps_values):for j, min_samples in enumerate(min_samples_values):# 创建DBSCAN实例dbscan = CustomDBSCAN(eps=eps, min_samples=min_samples)labels = dbscan.fit_predict(X)ax = axes[i, j]# 统计结果n_clusters = len(set(labels)) - (1 if -1 in labels else 0)n_noise = list(labels).count(-1)# 绘制聚类结果unique_labels = set(labels)colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]for k, col in zip(unique_labels, colors):if k == -1:col = [0, 0, 0, 1]class_member_mask = (labels == k)xy = X[class_member_mask]ax.plot(xy[:, 0], xy[:, 1], 'o',markerfacecolor=tuple(col),markeredgecolor='k',markersize=4)ax.set_title(f'eps={eps}, min_samples={min_samples}\n'f'Clusters: {n_clusters}, Noise: {n_noise}',fontsize=10)ax.grid(True, alpha=0.3)plt.tight_layout()plt.show()def find_optimal_eps(X, k=4):"""使用k-距离图找到最优eps:param X: 数据集:param k: 最近邻数量（通常取min_samples-1）"""from sklearn.neighbors import NearestNeighbors# 计算每个点到第k个最近邻的距离neighbors = NearestNeighbors(n_neighbors=k)neighbors_fit = neighbors.fit(X)distances, indices = neighbors_fit.kneighbors(X)# 按距离排序k_distances = np.sort(distances[:, k - 1], axis=0)# 绘制k-距离图plt.figure(figsize=(10, 6))plt.plot(k_distances)plt.xlabel('Points sorted by distance')plt.ylabel(f'{k}-th nearest neighbor distance')plt.title('K-Distance Graph for EPS selection')plt.grid(True, alpha=0.3)plt.show()# 寻找"拐点"（曲率最大的点）return k_distancesdef main_demo():"""主演示函数：展示DBSCAN的完整工作流程"""print("=" * 60)print("DBSCAN聚类算法完整演示")print("=" * 60)# 1. 数据生成print("\n1. 生成示例数据...")X = generate_sample_data()print(f"数据集形状: {X.shape} (样本数 × 特征数)")print(f"前5个样本点:\n{X[:5]}")# 2. 使用k-距离图寻找最优epsprint("\n2. 使用k-距离图寻找最优eps...")k_distances = find_optimal_eps(X, k=4)# 通常选择拐点处的eps值，这里我们手动选择0.3# 3. 自定义DBSCAN演示print("\n3. 使用自定义DBSCAN实现...")custom_dbscan = CustomDBSCAN(eps=0.3, min_samples=5)custom_labels = custom_dbscan.fit_predict(X)# 统计结果n_clusters_custom = len(set(custom_labels)) - (1 if -1 in custom_labels else 0)n_noise_custom = list(custom_labels).count(-1)print(f"自定义DBSCAN结果:")print(f"  - 发现簇数量: {n_clusters_custom}")print(f"  - 噪声点数量: {n_noise_custom}")print(f"  - 聚类标签分布: {np.unique(custom_labels, return_counts=True)}")# 可视化自定义DBSCAN结果plot_clustering_results(X, custom_labels, "自定义实现", "Custom DBSCAN")# 4. 与sklearn官方实现对比print("\n4. 与sklearn官方实现对比...")sklearn_dbscan = SklearnDBSCAN(eps=0.3, min_samples=5)sklearn_labels = sklearn_dbscan.fit_predict(X)n_clusters_sklearn = len(set(sklearn_labels)) - (1 if -1 in sklearn_labels else 0)n_noise_sklearn = list(sklearn_labels).count(-1)print(f"Sklearn DBSCAN结果:")print(f"  - 发现簇数量: {n_clusters_sklearn}")print(f"  - 噪声点数量: {n_noise_sklearn}")print(f"  - 聚类标签分布: {np.unique(sklearn_labels, return_counts=True)}")# 可视化sklearn结果plot_clustering_results(X, sklearn_labels, "官方库实现", "Sklearn DBSCAN")# 5. 算法性能比较print("\n5. 算法性能比较...")# 计算轮廓系数（聚类质量指标，-1到1，越大越好）if n_clusters_custom > 1:  # 轮廓系数需要至少2个簇custom_score = silhouette_score(X, custom_labels)sklearn_score = silhouette_score(X, sklearn_labels)print(f"轮廓系数比较:")print(f"  - 自定义DBSCAN: {custom_score:.4f}")print(f"  - Sklearn DBSCAN: {sklearn_score:.4f}")else:print("轮廓系数需要至少2个非噪声簇才能计算")# 6. 参数敏感性分析print("\n6. 进行参数敏感性分析...")analyze_parameters(X)# 7. 实用建议print("\n7. DBSCAN使用建议:")print("   ✅ eps选择: 使用k-距离图找到拐点")print("   ✅ min_samples: 从维度+1开始尝试")print("   ✅ 数据预处理: 必须进行标准化")print("   ✅ 噪声处理: 噪声点可用于异常检测")print("   ✅ 适用场景: 任意形状簇、有噪声数据")return X, custom_labels, sklearn_labels# 运行主程序
if __name__ == "__main__":# 执行演示X, custom_labels, sklearn_labels = main_demo()print("\n" + "=" * 60)print("演示完成！")print("=" * 60)
```
http://www.dtcms.com/a/488461.html

相关文章：

  • 哪些网站推广不收费网站设计 原型图
  • yolo v8n模型小样本微调总结
  • 网站制作 呼和浩特南山网站设计方案
  • 如何做家居网站注册公司一年需要多少费用
  • 专门做酒店设计的网站网页设计参考网站
  • 网页设计制作网站首页建筑网建设通网站作用是什么
  • 猎头可以做单的网站做网站的图片大小是多少
  • 盘州市网站建设调用别人网站的数据库
  • 国外设计网站素材网站打开显示站点目录
  • 网址制作网站云南网官网入口
  • 雄安智能网站建设公司郑州的网站建设
  • 大庆网站建设公司台州网站建设网站
  • 建设网站西安万网做网站多少钱
  • 红星美凯龙建设事业中心网站大数据精准营销论文
  • 备案号链接工信部网站3d设计房子的软件
  • rhce第一次作业
  • 【Shell编程学习】Shell基础知识
  • 征婚网站开发呼市网站制作
  • 扬州西区网站建设安康手机网站建设
  • html5自适应网站模版打鱼网站怎么做
  • 新乡高端网站建设app定制开发深圳
  • [Qlib] 回测执行 | `backtest_daily`日频回测
  • 简洁商城网站模板网站终端制作
  • P11215 【MX-J8-T3】水星湖
  • 温湿度传感器技术深度解析：从测量原理到工程落地
  • 将 localhost 代理配置镜像到 WSL
  • 企业展示网站如何建wordpress 打开慢 google
  • 餐饮网站欣赏wordpress 归档页面地址
  • 网站优化目标旅游营销型网站
  • 防钓鱼网站宣传深圳网站建设与制作公司