计算机组成原理01-定点数/浮点数的原/反/补码运算
目录
一定点数/浮点数的原/反/补码运算
1补码加减运算电路
2无符号整数的乘法运算原理
3总结
一定点数/浮点数的原/反/补码运算
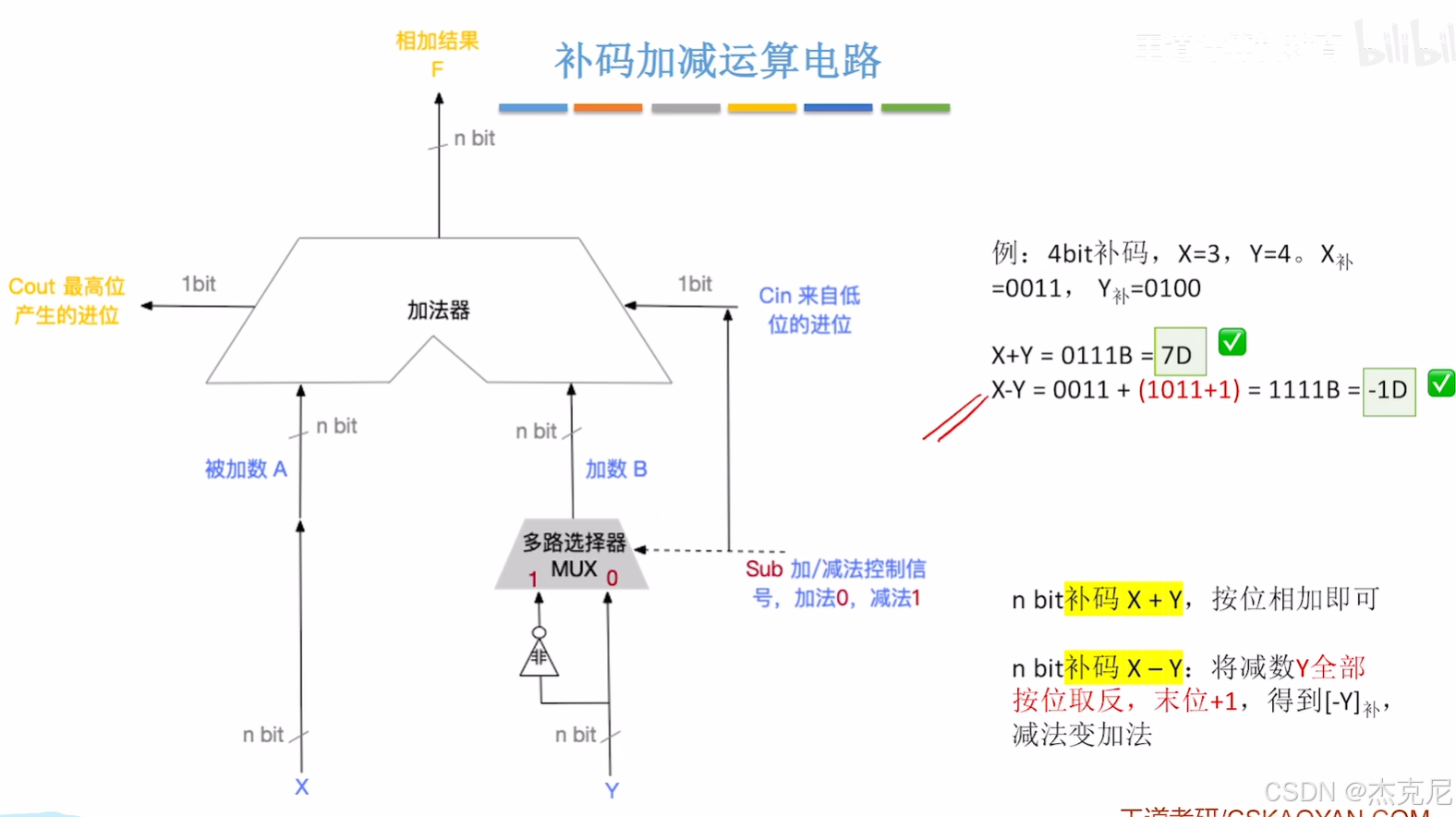
1补码加减运算电路


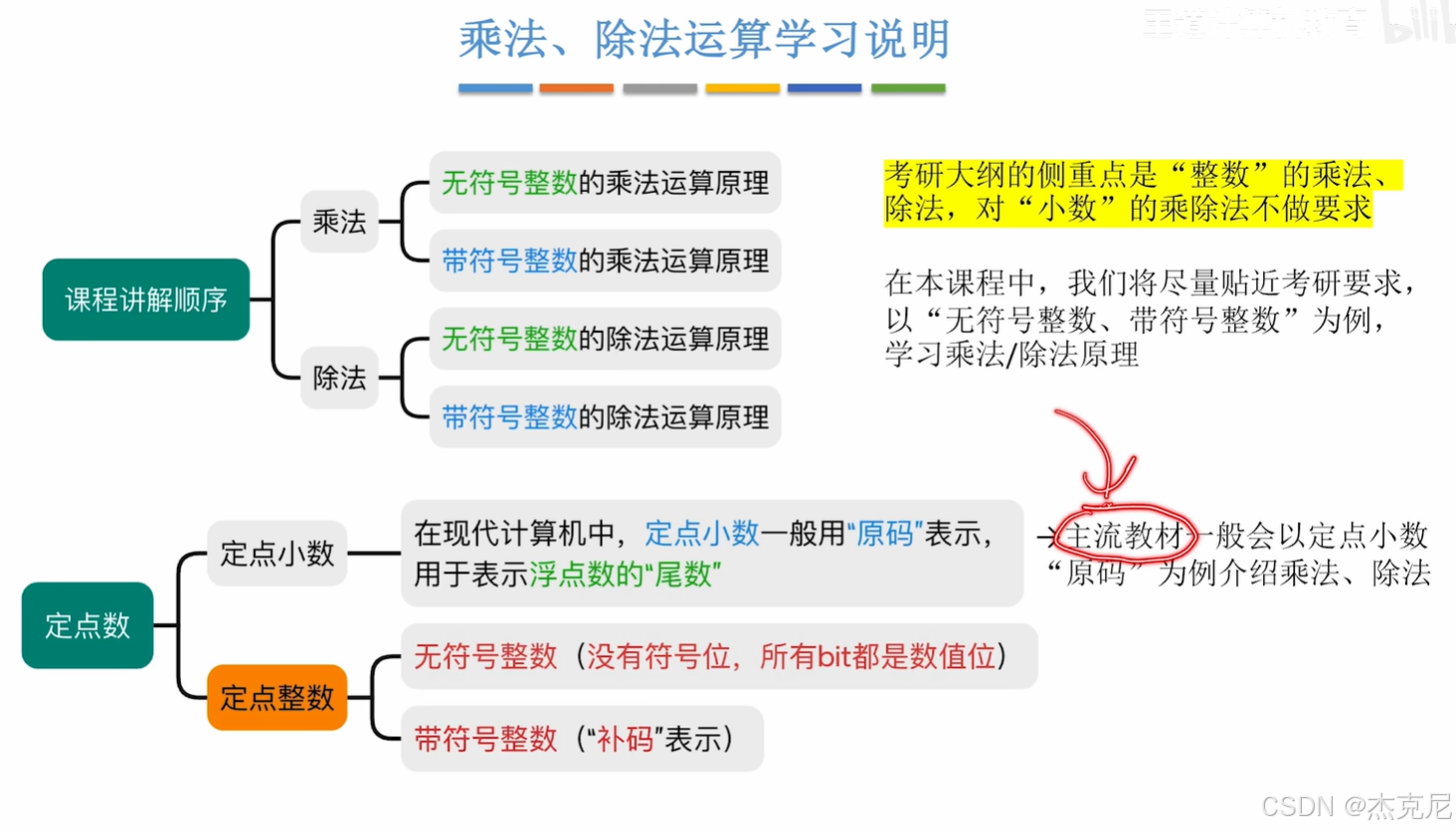
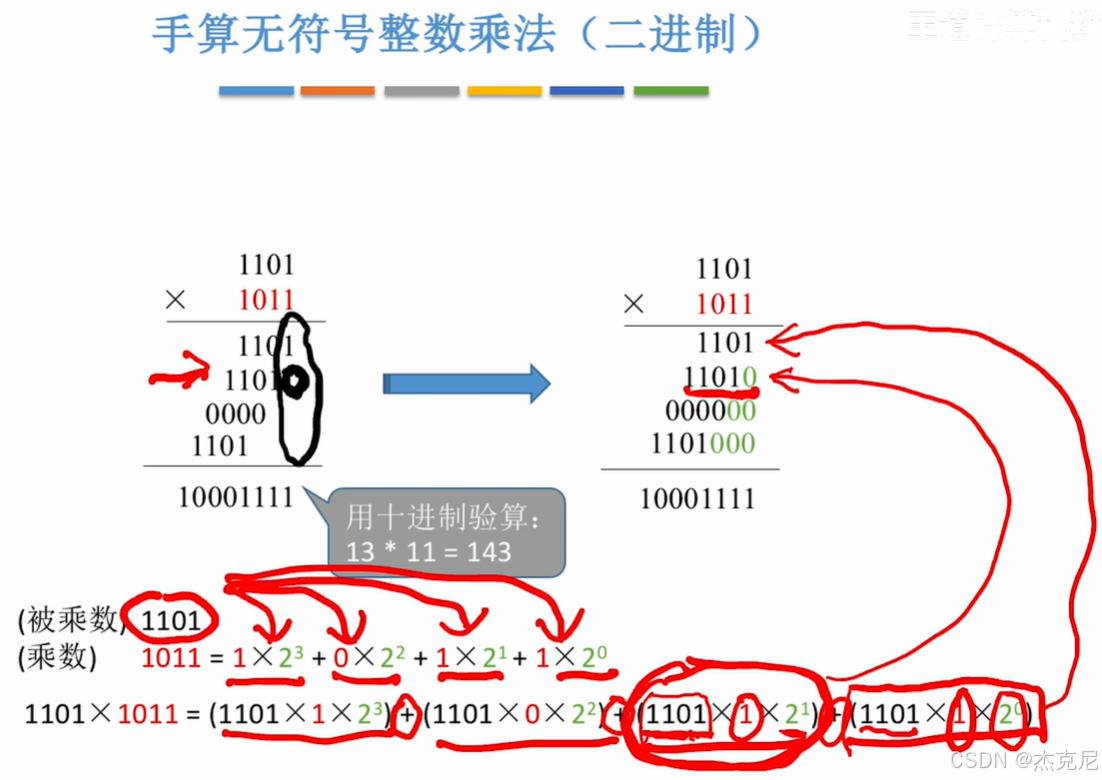
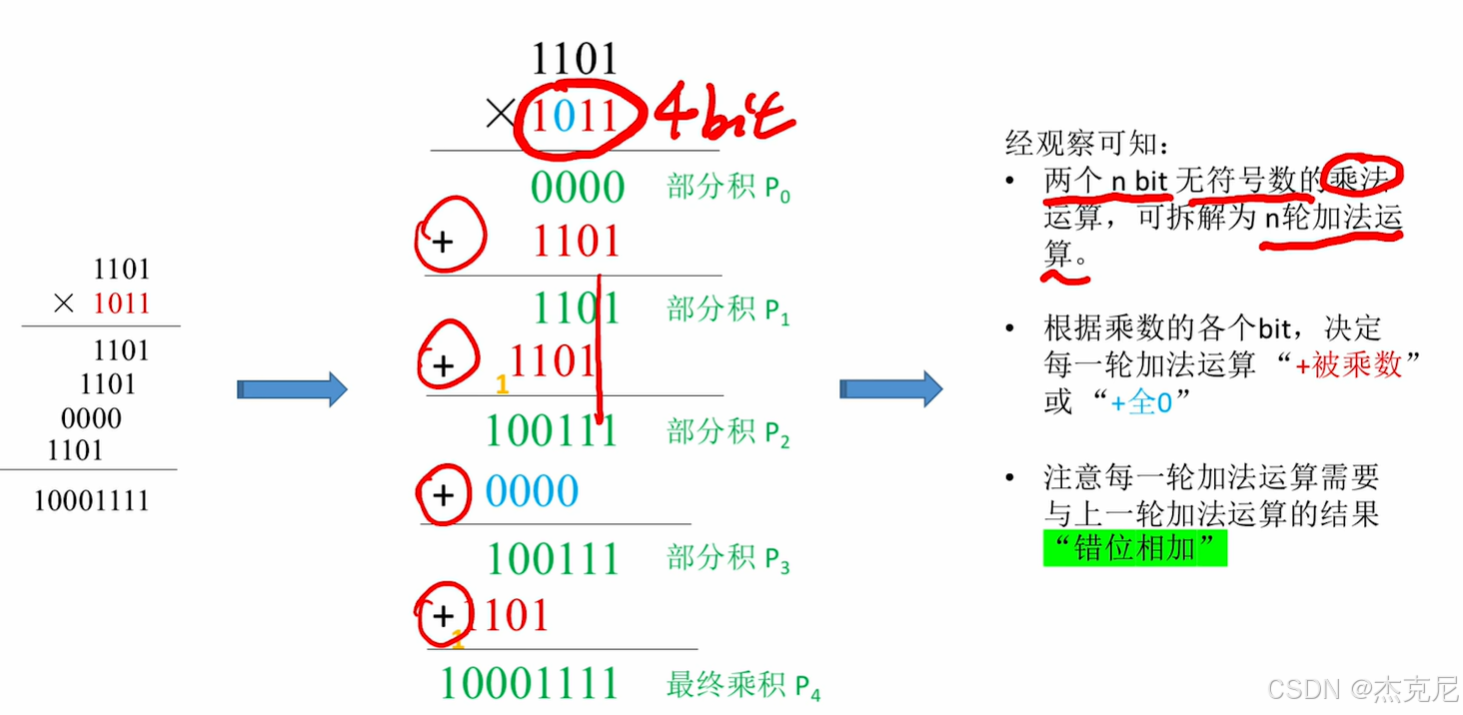
2无符号整数的乘法运算原理

3总结
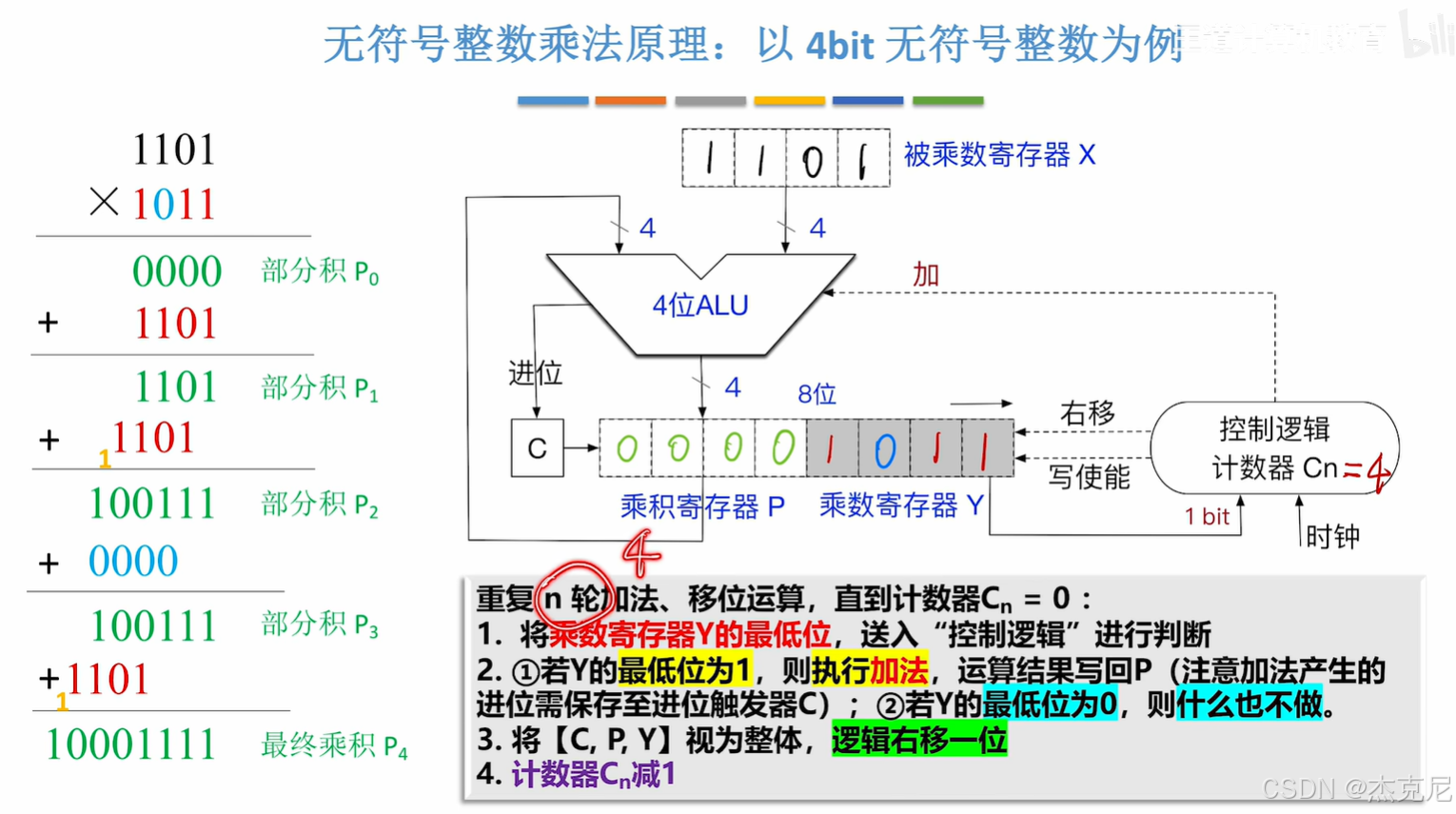
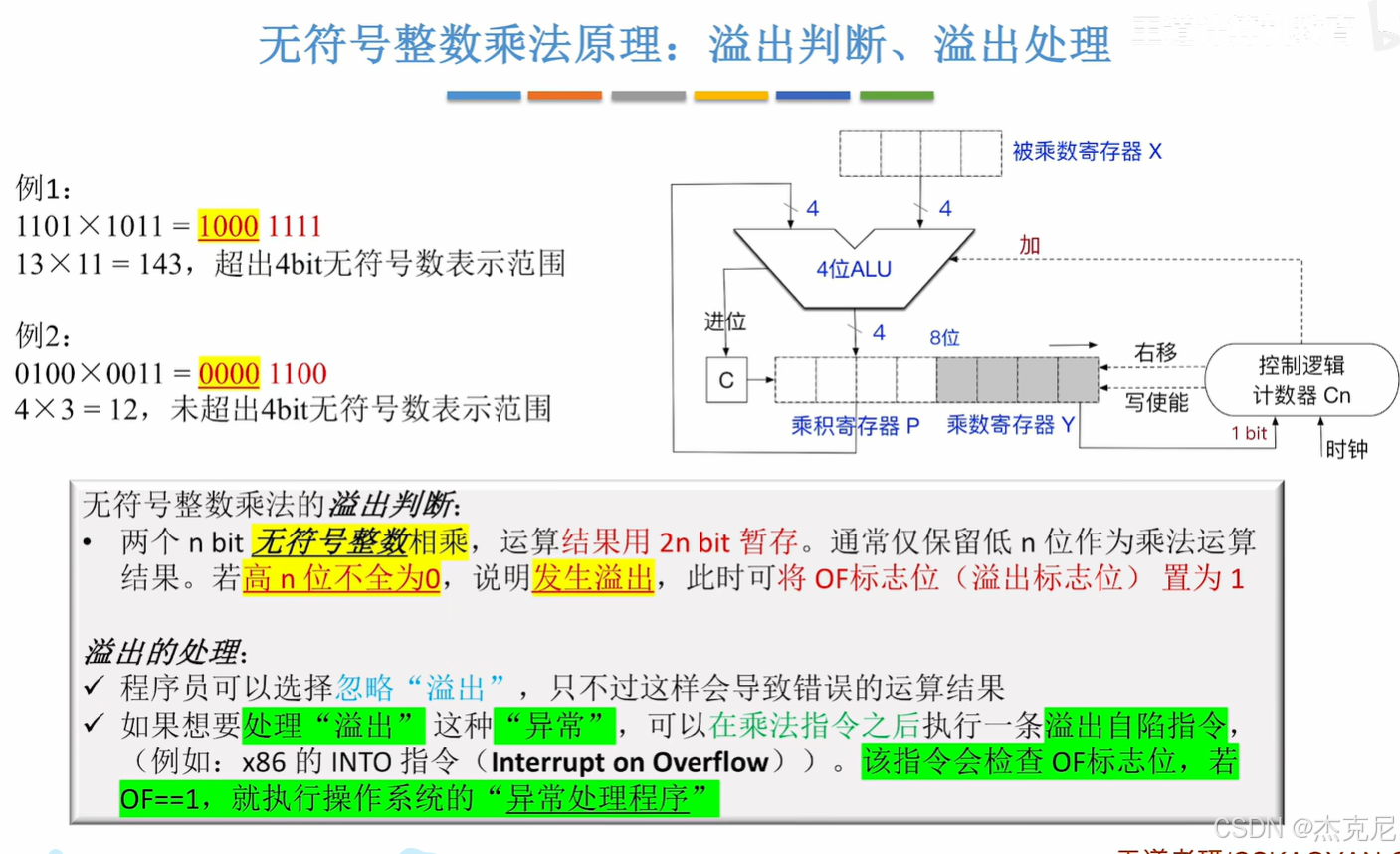
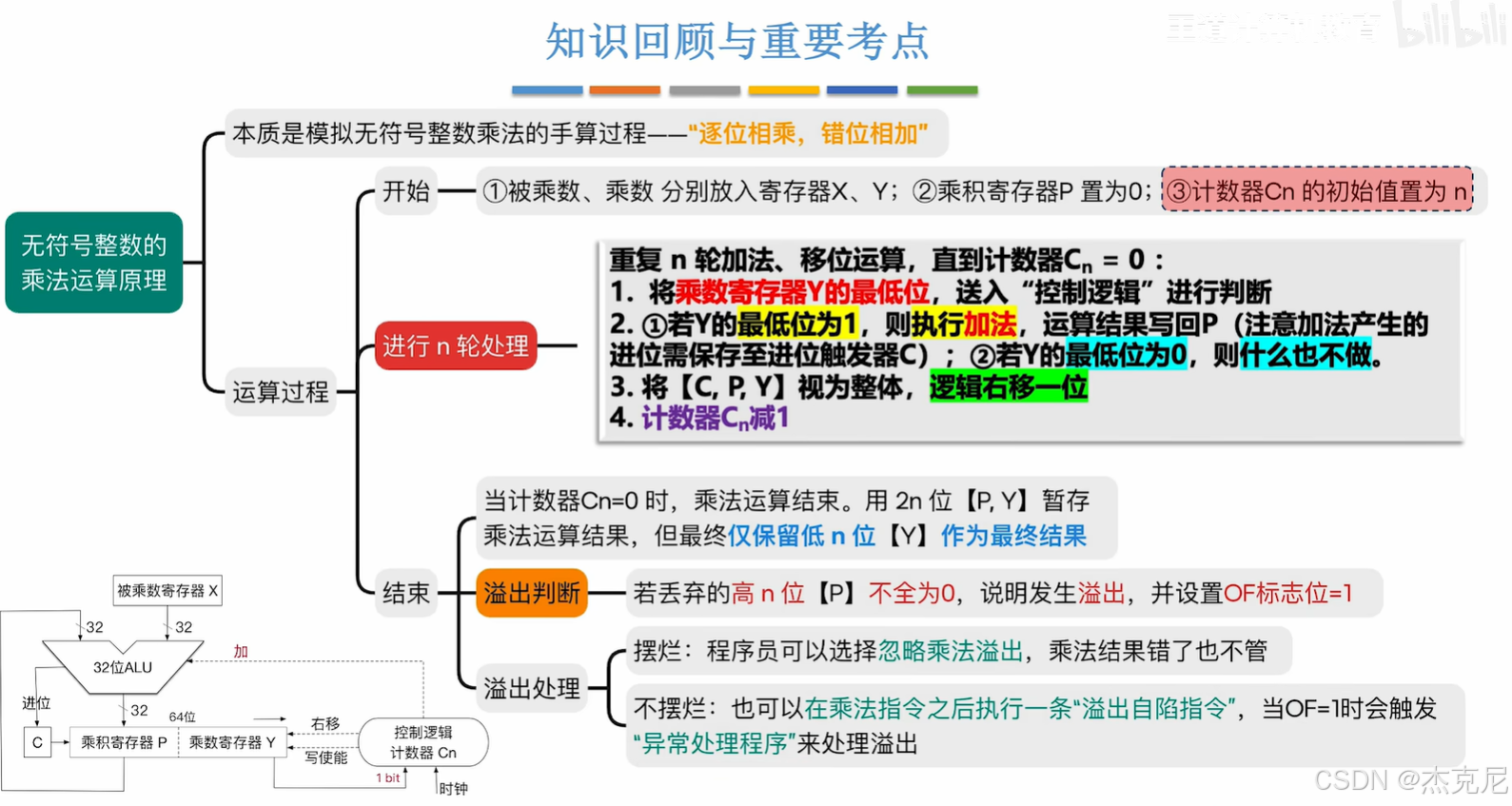
计算机组成原理:无符号整数乘法运算的底层逻辑探秘在计算机的运算世界里,乘法是最基础也最具技术含量的操作之一。与人类可以通过背诵乘法口诀快速计算不同,计算机实现无符号整数乘法,需要模拟 “手算乘法” 的核心逻辑,并通过硬件电路的协作,完成高效且精准的运算。今天,我们就从 “原理本质”“运算过程”“溢出处理” 三个维度,深度解析无符号整数乘法的底层实现。一、本质:模拟手算乘法的 “逐位相乘,错位相加”手算乘法的启示回忆小学时计算乘法的过程:比如计算 \(13 \times 12\),我们会将其拆解为 “\(13 \times 2 + 13 \times 10\)”,也就是逐位相乘,再错位相加。计算机的无符号整数乘法,本质上就是对这一过程的 “硬件级模拟”。只不过,由于计算机以二进制为基础,“逐位” 的粒度变成了 “每一个二进制位”。二进制手算乘法示例以 \(5_{10} \times 3_{10}\) 为例(二进制为 \(101_2 \times 011_2\)):乘数 \(011_2\) 的最低位是 1,计算 \(101_2 \times 1\),结果为 \(101_2\);乘数右移一位,新的最低位是 1,计算 \(101_2 \times 1\),结果左移一位(错位),得到 \(1010_2\);乘数再右移一位,新的最低位是 0,这一步 “什么也不做”;最后将所有结果相加:\(101_2 + 1010_2 = 1111_2 = 15_{10}\),与 \(5 \times 3 = 15\) 一致。计算机的无符号乘法,就是把这样的 “逐位判断、条件相加、错位右移” 过程,通过硬件电路自动化执行。二、运算过程:寄存器与控制逻辑的协作无符号整数乘法的硬件实现,依赖寄存器(存储数据)、算术逻辑单元(ALU)(执行加法)、控制逻辑(判断与流程控制)的协同工作。下面详细拆解每一个步骤。1. 初始化:数据与计数器的准备在乘法开始前,需要完成三项关键初始化:被乘数、乘数的存储:将被乘数放入寄存器 X,乘数放入寄存器 Y。假设被乘数和乘数都是 n 位无符号整数。乘积寄存器清零:乘积寄存器 P 初始化为 0,用于存储中间结果和最终乘积。计数器初始化:计数器 \(C_n\) 的初始值设为 n,它的作用是控制乘法的 “轮数”—— 因为要处理乘数的每一个二进制位,所以需要循环 n 次。2. n 轮核心操作:加法、移位与计数接下来,要重复 n 轮 “判断 - 加法 - 移位 - 计数” 操作,直到计数器 \(C_n = 0\)。每一轮的逻辑如下:步骤 1:判断乘数的最低位将乘数寄存器 Y 的最低位送入 “控制逻辑” 进行判断:如果 Y 的最低位为 1:说明当前位需要 “累加被乘数”;如果 Y 的最低位为 0:说明当前位不需要操作,直接进入下一步。步骤 2:条件加法(若最低位为 1)若 Y 的最低位为 1,则执行加法操作:将被乘数寄存器 X 中的值,与乘积寄存器 P 中的值,送入 ALU 进行加法运算;加法产生的进位,需要保存到进位触发器 C 中(因为 n 位加法可能产生进位,影响后续运算);加法的结果,写回乘积寄存器 P。若 Y 的最低位为 0,则 “什么也不做”,直接跳过加法步骤。步骤 3:整体右移将 \([C, P, Y]\) 视为一个整体,进行逻辑右移一位:C(进位触发器)的内容,移入 P 的最高位;P 的内容,依次右移,最低位移入 Y 的最高位;Y 的内容,依次右移,最低位被移出(不再参与后续判断)。这样做的目的是为下一轮操作 “腾出位置”:既保留了加法的进位信息,又让乘数的 “下一位” 移动到最低位,方便下一轮判断。步骤 4:计数器减 1将计数器 \(C_n\) 的值减 1,表示 “已经完成一轮操作”。3. 结束:结果存储与溢出判断当计数器 \(C_n = 0\) 时,n 轮操作全部完成,乘法运算的核心过程结束。此时:结果存储最终的乘法结果,暂存在 2n 位的 \([P, Y]\) 中:P 存储的是 “高 n 位” 结果;Y 存储的是 “低 n 位” 结果。但根据无符号整数乘法的规则,最终只保留低 n 位 Y 作为结果(因为 n 位无符号整数相乘,结果理论上最多为 2n 位,但实际应用中常取低 n 位,或通过溢出判断处理高 n 位)。三、溢出判断:高 n 位的 “有效性”无符号整数乘法的一个关键问题是溢出—— 当两个 n 位无符号整数相乘,结果可能超过 n 位的表示范围。溢出的判断逻辑当乘法结束后,若 “丢弃的高 n 位 P”不全为 0,说明发生了溢出:例如,8 位无符号整数 \(255 \times 2\),结果为 510,二进制是 \(111111110_2\)。若只保留低 8 位 \(11111110_2\)(即 254),与实际结果 510 不符,此时高 1 位 P 为 1(不全为 0),说明溢出。此时,会设置溢出标志位 \(OF = 1\),用于告知软件 “乘法结果超出了低 n 位的表示范围”。溢出的处理策略对于溢出,程序员有两种典型处理方式:策略 1:“摆烂”—— 忽略溢出如果应用场景对精度要求不高,或者认为 “溢出是可接受的误差”,可以选择忽略溢出。此时,乘法结果直接取低 n 位 Y,即使它是错误的。策略 2:“不摆烂”—— 异常处理如果应用场景要求精准,就需要处理溢出。通常的做法是:在乘法指令之后,执行一条 **“溢出自陷指令”**;当溢出标志位 \(OF = 1\) 时,该指令会触发 **“异常处理程序”**,由程序来决定如何处理(如报错、使用更大范围的变量存储结果等)。四、硬件架构的支撑:各组件的分工与协作为了更直观理解无符号乘法的硬件执行,我们可以梳理各核心组件的角色:1. 寄存器组被乘数寄存器 X:固定存储被乘数,在整个乘法过程中保持不变。乘数寄存器 Y:存储乘数,并在每一轮右移中,逐步 “消耗” 每一位(最低位被判断后,右移腾出下一位)。乘积寄存器 P:存储加法的中间结果,最终存储高 n 位结果。进位触发器 C:存储加法产生的进位,确保进位信息在右移中被正确传递。2. 算术逻辑单元(ALU)ALU 是执行加法的核心部件,负责 “被乘数 X + 乘积 P” 的运算,并将结果写回 P。3. 控制逻辑与计数器控制逻辑:判断乘数 Y 的最低位是 0 还是 1,决定是否触发加法操作。计数器 \(C_n\):控制乘法的轮数,确保 n 位乘数的每一位都被处理。4. 移位电路负责将 \([C, P, Y]\) 作为整体进行逻辑右移,实现 “错位” 的硬件化。五、总结:从手算到硬件的 “自动化升级”无符号整数乘法的底层实现,是对人类 “手算乘法” 的一次 “硬件级自动化改造”:它通过 **“逐位判断、条件加法、整体右移”** 的循环,模拟了 “逐位相乘,错位相加” 的核心逻辑;它依赖寄存器、ALU、控制逻辑、移位电路的协同,将手动计算的步骤转化为硬件的自动执行;它通过溢出判断与处理,保证了运算结果的可靠性(或让程序员有机会处理误差)。理解这一过程,不仅能帮助我们掌握计算机运算的底层机制,更能体会到 “抽象逻辑(手算乘法)→ 硬件实现(寄存器与电路)” 的计算机科学核心思想 —— 这也是计算机组成原理这门学科的魅力所在。
