当前位置： 首页 > news >正文

数据结构 04 栈和队列

news 2025/10/15 16:02:02

1 链栈基本操作的实现

链栈是一种基于链表实现的栈结构，栈遵循 “先进后出”（FILO）的原则。下面详细解释链栈的基本操作，并给出代码实现（以 C 语言为例）。

1. 链栈的结构定义

首先需要定义链栈的结点结构，每个结点包含数据域和指针域：

typedef struct StackNode {int data;               // 数据域，存储栈中元素struct StackNode *next; // 指针域，指向下一个结点
} StackNode;typedef struct {StackNode *top; // 栈顶指针，指向链栈的栈顶结点
} LinkStack;

2. 初始化（Initialization）

初始化链栈时，将栈顶指针设置为 NULL，表示栈为空：

void InitStack(LinkStack *S) {S->top = NULL; // 栈顶指针置空，链栈初始为空
}
  • 解释：此时链栈中没有任何结点，top 指向 NULL，后续入栈操作会从这里开始构建链栈。

3. 入栈（Push）

入栈操作是在栈顶添加一个新的元素，步骤如下：

  1. 申请一个新的结点 p。
  2. 将待入栈的元素 e 存入新结点的数据域。
  3. 将新结点的 next 指针指向当前的栈顶结点（因为新结点要成为新的栈顶，所以要先连接原来的栈顶）。
  4. 将栈顶指针 top 指向新结点，使其成为新的栈顶。

代码实现：

int Push(LinkStack *S, int e) {StackNode *p = (StackNode *)malloc(sizeof(StackNode)); // 申请新结点if (p == NULL) {return 0; // 内存分配失败，入栈失败}p->data = e;        // 存入数据p->next = S->top;   // 新结点的 next 指向原栈顶S->top = p;         // 栈顶指针指向新结点，新结点成为栈顶return 1;           // 入栈成功
}
  • 解释：比如原来栈顶是结点 A，现在入栈元素 B，新结点 p 的 next 指向 A，然后 top 指向 p，此时栈顶就是 B 了，符合 “先进后出”，后续出栈会先取出 B。

4. 判空（Empty）

判断链栈是否为空，只需检查栈顶指针是否为 NULL：

int IsEmpty(LinkStack S) {return S.top == NULL; // 栈顶指针为 NULL 则栈空，返回 1；否则返回 0
}
  • 解释：如果 top 是 NULL，说明链栈中没有结点，栈为空；否则栈不为空。

5. 出栈（Pop）

出栈操作是从栈顶取出一个元素，步骤如下：

  1. 先判断栈是否为空，如果为空则无法出栈。
  2. 如果栈不为空，记录栈顶结点的数据。
  3. 将栈顶指针指向栈顶结点的下一个结点（原来的第二个结点成为新的栈顶）。
  4. 释放原来的栈顶结点的内存。

代码实现：

int Pop(LinkStack *S, int *e) {if (IsEmpty(*S)) {return 0; // 栈空，出栈失败}StackNode *p = S->top; // 暂存栈顶结点*e = p->data;          // 获取栈顶元素的数据S->top = p->next;      // 栈顶指针指向原栈顶的下一个结点free(p);               // 释放原栈顶结点的内存return 1;              // 出栈成功
}
  • 解释：比如栈顶是结点 B，其 next 指向结点 A，出栈时，先取出 B 的数据，然后 top 指向 A，释放 B 的内存，此时栈顶就是 A 了，下次出栈就会取出 A。

完整示例代码

下面是包含所有操作的完整示例，还添加了获取栈顶元素和遍历栈的函数：

#include <stdio.h>
#include <stdlib.h>typedef struct StackNode {int data;struct StackNode *next;
} StackNode;typedef struct {StackNode *top;
} LinkStack;// 初始化链栈
void InitStack(LinkStack *S) {S->top = NULL;
}// 入栈
int Push(LinkStack *S, int e) {StackNode *p = (StackNode *)malloc(sizeof(StackNode));if (p == NULL) {return 0;}p->data = e;p->next = S->top;S->top = p;return 1;
}// 判空
int IsEmpty(LinkStack S) {return S.top == NULL;
}// 出栈
int Pop(LinkStack *S, int *e) {if (IsEmpty(*S)) {return 0;}StackNode *p = S->top;*e = p->data;S->top = p->next;free(p);return 1;
}// 获取栈顶元素（不出栈）
int GetTop(LinkStack S, int *e) {if (IsEmpty(S)) {return 0;}*e = S.top->data;return 1;
}// 遍历栈（从栈顶到栈底）
void TraverseStack(LinkStack S) {StackNode *p = S.top;printf("栈中元素（从栈顶到栈底）：");while (p != NULL) {printf("%d ", p->data);p = p->next;}printf("\n");
}int main() {LinkStack S;InitStack(&S);// 入栈操作Push(&S, 1);Push(&S, 2);Push(&S, 3);Push(&S, 4);TraverseStack(S); // 输出：栈中元素（从栈顶到栈底）：4 3 2 1 int topElem;GetTop(S, &topElem);printf("栈顶元素：%d\n", topElem); // 输出：栈顶元素：4// 出栈操作int popElem;Pop(&S, &popElem);printf("出栈元素：%d\n", popElem); // 输出：出栈元素：4TraverseStack(S); // 输出：栈中元素（从栈顶到栈底）：3 2 1 return 0;
}

2 课件PPT关于括号检查的解法

Leetcode 27-CSDN博客https://blog.csdn.net/AYheyheyhey/article/details/153258951?spm=1001.2014.3001.5501

区别在于这个基础是链栈，题目可以看卡片附上的。

3 队列以及其基本操作

这是队列的抽象数据类型（ADT）定义，队列是一种 ** 先进先出（FIFO）** 的线性数据结构，类似排队，先到的先处理。下面详细解释各部分并给出基于链式存储的 C 语言实现。

一、解释

  1. 基本操作：

    • InitQueue(&Q)：初始化队列 Q，使其成为空队列。
    • DestroyQueue(&Q)：销毁队列 Q，释放所有资源。
    • QueueEmpty(Q)：判断队列 Q 是否为空，返回布尔值。
    • QueueLength(Q)：返回队列 Q 的长度（元素个数）。
    • GetHead(Q, &e)：获取队头元素，存入 e（不删除队头）。
    • EnQueue(&Q, e)：将元素 e 入队（添加到队尾）。
    • DeQueue(&Q, &e)：出队（删除队头元素），并将队头元素存入 e。

二、链式队列的 C 语言实现

队列的存储有顺序存储（数组）和链式存储（链表）两种方式。这里用链式存储（更灵活，无固定容量限制）实现，步骤如下：

1. 定义结构体
// 队列结点结构
typedef struct QNode {int data;           // 数据域（假设元素是 int 型，可根据需求修改）struct QNode *next; // 指针域，指向下一个结点
} QNode, *QueuePtr;// 队列结构（包含队头、队尾指针）
typedef struct {QueuePtr front; // 队头指针QueuePtr rear;  // 队尾指针
} LinkQueue;
2. 初始化队列 InitQueue
void InitQueue(LinkQueue *Q) {// 创建头结点（不存数据，仅用于统一操作）Q->front = Q->rear = (QueuePtr)malloc(sizeof(QNode));if (Q->front == NULL) {printf("内存分配失败！\n");exit(1); // 异常退出}Q->front->next = NULL; // 头结点 next 置空（队列为空）
}
3. 销毁队列 DestroyQueue
void DestroyQueue(LinkQueue *Q) {// 循环释放所有结点，直到队头为 NULLwhile (Q->front) {Q->rear = Q->front->next; // 暂存下一个结点free(Q->front);           // 释放当前队头Q->front = Q->rear;       // 队头后移}
}
4. 判断队列是否为空 QueueEmpty
int QueueEmpty(LinkQueue Q) {// 队头和队尾指向同一结点（头结点），则为空return Q.front == Q.rear;
}
5. 队列长度 QueueLength
int QueueLength(LinkQueue Q) {int len = 0;QueuePtr p = Q.front->next; // 从第一个元素结点开始遍历while (p) {len++;p = p->next;}return len;
}
6. 获取队头元素 GetHead
int GetHead(LinkQueue Q, int *e) {if (QueueEmpty(Q)) {return 0; // 队空，获取失败}*e = Q.front->next->data; // 队头元素是头结点的下一个结点的数据return 1; // 获取成功
}
7. 入队 EnQueue
int EnQueue(LinkQueue *Q, int e) {QueuePtr p = (QueuePtr)malloc(sizeof(QNode));if (p == NULL) {printf("内存分配失败！\n");return 0; // 分配失败，入队失败}p->data = e;   // 存入数据p->next = NULL; // 新结点为队尾，next 置空Q->rear->next = p; // 原队尾的 next 指向新结点Q->rear = p;       // 队尾指针指向新结点return 1; // 入队成功
}
8. 出队 DeQueue
int DeQueue(LinkQueue *Q, int *e) {if (QueueEmpty(Q)) {return 0; // 队空，出队失败}QueuePtr p = Q.front->next; // 暂存队头元素结点*e = p->data;               // 获取队头元素Q->front->next = p->next;   // 头结点的 next 指向原队头的下一个结点if (Q->rear == p) {Q->rear = Q->front; // 若队中只有一个元素，出队后队尾指向头结点}free(p); // 释放原队头结点return 1; // 出队成功
}

三、测试示例

int main() {LinkQueue Q;InitQueue(&Q); // 初始化队列// 入队测试EnQueue(&Q, 1);EnQueue(&Q, 2);EnQueue(&Q, 3);// 队列长度printf("队列长度：%d\n", QueueLength(Q)); // 输出：3// 获取队头int head;GetHead(Q, &head);printf("队头元素：%d\n", head); // 输出：1// 出队测试int e;DeQueue(&Q, &e);printf("出队元素：%d\n", e); // 输出：1// 再次获取队头GetHead(Q, &head);printf("新队头元素：%d\n", head); // 输出：2// 销毁队列DestroyQueue(&Q);return 0;
}

四、总结

队列的核心是先进先出，链式实现通过 “头指针 + 尾指针” 快速操作队头和队尾，适合频繁入队 / 出队的场景（如任务调度、消息队列等）。若需固定容量，也可改用 ** 顺序存储（数组）** 实现（需处理 “假溢出” 问题，通常用循环队列优化）。

4 顺序队列的“溢出”问题

一、顺序队列的存储基础

顺序队列是用数组来存储队列元素的，就像一个固定长度的 “管子”。数组有两个关键的指针（其实是下标）：

  • front：队头指针，指向队列中第一个元素的位置。
  • rear：队尾指针，指向队列中最后一个元素的下一个位置（这样方便操作）。还有一个 MaxSize，表示数组的最大容量（队列最多能存多少元素）。

二、真溢出（真正的没地方了）

当 rear - front ≥ MaxSize 时，就发生了真溢出。

  • 解释：rear - front 可以理解为当前队列中元素的个数（因为 rear 指向队尾下一个位置，front 指向队头）。当这个差值大于等于数组最大容量 MaxSize 时，说明数组里真的装满了，没有任何空闲位置可以再入队了。
  • 比如：数组能存 5 个元素（MaxSize = 5），现在队列里已经有 5 个元素了（rear - front = 5），这时候再想入队，就没地方了，这就是真溢出。

三、假溢出（有地方但装不下）

假溢出是顺序队列很 “坑” 的一个问题：数组还有空闲空间，但因为队头和队尾的位置，导致无法入队。

  • 例子：假设数组长度是 5，一开始队列是空的（front = rear = 0）。然后进行了 3 次入队（元素存在下标 0、1、2），再进行 2 次出队（把下标 0、1 的元素删了）。这时候队列里只有下标 2 的元素，front 移到了 2，rear 还是 3。现在数组下标 0、1 是空闲的，但如果要入队，rear 想往后移，可后面没位置了（因为 rear 到 4 就到数组末尾了），但其实前面 0、1 是空的。这就是 “假溢出”—— 有空间，但因为队列的 “头重脚轻”，没法用。

四、解决假溢出的方法

方法 1：按最大需求设置队列大小
  • 解释：如果能预估队列最多需要存多少元素，就把数组 MaxSize 设得足够大，大到能装下所有可能的入队元素。
  • 比如：你知道程序里最多会同时有 100 个元素在队列里，那你就把数组设为能存 100 个元素。这样只要元素个数不超过 100，就不会溢出。
  • 缺点：如果预估错了，或者元素个数波动大，要么浪费空间（设太大），要么还是会溢出（设太小）。
方法 2：出队后，剩余元素向队头移动
  • 解释：每次出队（删除队头元素）后，把队列里剩下的所有元素，都往队头方向挪一个位置。这样队尾的位置就空出来了，后续入队可以继续用。
  • 例子：队列里元素是 [a, b, c]（front=0，rear=3），出队 a 后，把 b 移到下标 0，c 移到下标 1，rear 变成 2。这样下次入队，元素就可以存在下标 2 的位置。
  • 缺点：每次出队都要移动所有元素，效率很低（比如队列有 1000 个元素，每次出队都要移 999 个，特别费时间）。
方法 3：入队时，先移动元素再入队
  • 解释：当要入队时，先检查是不是假溢出。如果是，就把队列里已有的元素往队头方向挪，腾出队尾的位置，然后再把新元素入队。
  • 例子：队列元素存在 [_, _, c]（front=2，rear=3，数组长度 5），现在要入队 d。发现 rear 到末尾了，就把 c 移到下标 0，然后 d 存在下标 1，front=0，rear=2。
  • 缺点：和方法 2 一样，移动元素很费时间，效率不高。
方法 4：采用循环队列（最常用、最聪明的方法）
  • 核心思想：把数组想象成一个环，队头和队尾可以 “绕圈”。当 rear 到数组末尾时，下一个位置可以回到数组开头（用取模运算实现）。
  • 实现要点：
    • 入队时：rear = (rear + 1) % MaxSize。这样当 rear 到 MaxSize - 1 时，(rear + 1) % MaxSize 就会回到 0。
    • 出队时：front = (front + 1) % MaxSize。
    • 判空：front == rear（和普通顺序队列一样）。
    • 判满：通常用 “牺牲一个空间” 的方法，即 (rear + 1) % MaxSize == front 时，认为队列满了。
  • 例子：数组长度 5，front=2，rear=4。现在入队，rear = (4 + 1) % 5 = 0，元素存在下标 0 的位置。这样就利用了数组开头的空闲空间，解决了假溢出。
  • 优点：不用移动元素，效率高，还能充分利用数组空间。

5 循环队列

一、循环队列的基本思想

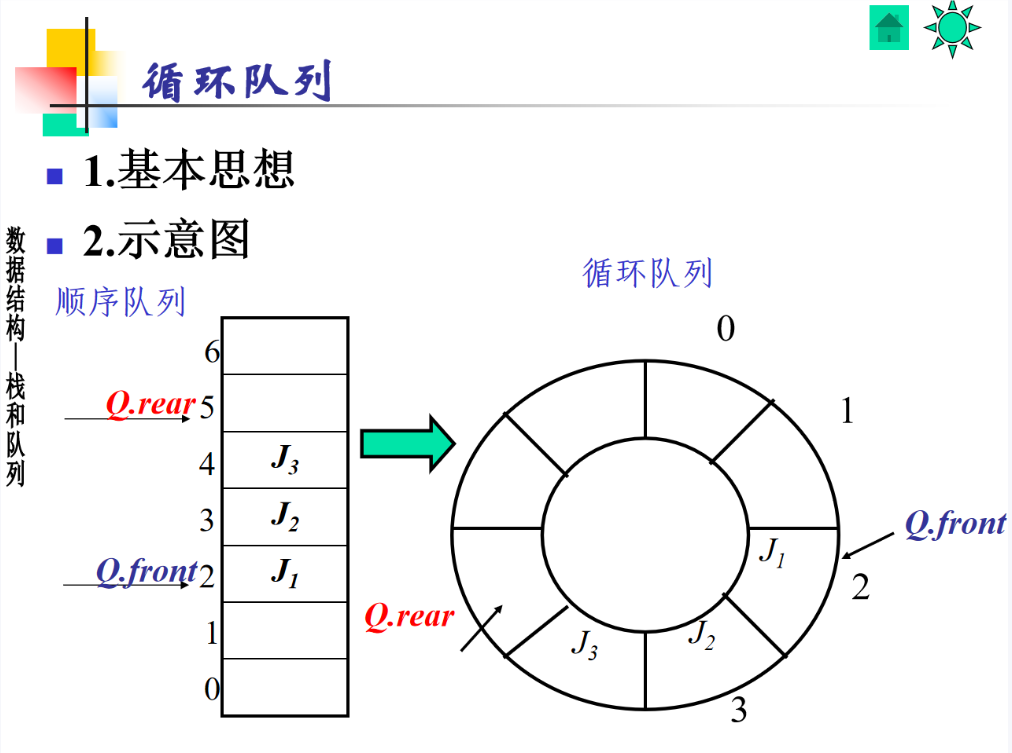
顺序队列会有 “假溢出” 问题（前面有空位，但队尾到数组末尾了，没法入队）。循环队列的想法是：把数组想象成一个环，队头和队尾可以 “绕圈”。比如数组最后一个位置的下一个位置，不是越界，而是回到数组开头。这样就能充分利用数组的所有空间，解决假溢出。

二、循环队列的示意图

左边是顺序队列：数组下标从 0 到 6，队头 Q.front 在 2，队尾 Q.rear 在 5，元素是 J₁（下标 2）、J₂（下标 3）、J₃（下标 4）。这时候如果再入队，rear 到 6 就没地方了，但其实下标 0、1 是空的。

右边是循环队列：把数组变成一个环，下标 0 接在 6 后面。队头 Q.front 在 2，队尾 Q.rear 绕到后面，元素 J₁、J₂、J₃ 像绕圈一样排列，这样前面的空位（下标 0、1）就可以被利用了。

三、循环队列的 “二义性” 问题

在循环队列里，队空的条件是 Q.front == Q.rear（队头和队尾重合，没有元素）。但如果队列满了，有时候也会出现 Q.front == Q.rear（比如数组全装满了，队头和队尾绕圈后重合）。这就导致 “Q.front == Q.rear” 既可能是队空，也可能是队满，这就是二义性（一个条件有两种意思，没法判断）。

四、解决二义性的三种方法

方法 1：用计数器记录元素个数
  • 思路：搞一个变量 count，专门记录队列里有多少个元素。
  • 判队空：count == 0（队列里一个元素都没有）。
  • 判队满：count == MAXQSIZE（MAXQSIZE 是数组最大容量，元素个数达到上限）。
  • 解释：因为有 count 明确记录个数，所以不管 Q.front 和 Q.rear 怎么绕，只要看 count 就知道是满还是空。
方法 2：加设标志位 tag
  • 思路：用 tag 标记最近一次操作是 “入队” 还是 “出队”。
    • tag = 0：最近一次是出队操作。
    • tag = 1：最近一次是入队操作。
  • 判队空：tag == 0 && Q.rear == Q.front（最近是出队，现在队头队尾重合，说明队空了）。
  • 判队满：tag == 1 && Q.rear == Q.front（最近是入队，现在队头队尾重合，说明队满了，因为入队导致没地方了）。
  • 解释：通过 tag 区分 “是出队导致的重合（队空）” 还是 “入队导致的重合（队满）”。
方法 3：少用一个存储单元
  • 思路：故意让数组少用一个位置，这样队满和队空的条件就不一样了。
  • 判队空：Q.rear == Q.front（和原来一样）。
  • 判队满：Q.front == (Q.rear + 1) % MAXQSIZE（队尾的下一个位置是队头，说明队满了）。
  • 例子：数组最大容量 MAXQSIZE = 5，实际只用 4 个位置存元素。当 Q.rear 在 4，(Q.rear + 1) % 5 = 0，如果此时 Q.front = 0，就说明队满了（队尾的下一个位置是队头）。
  • 解释：因为少用了一个位置，所以队满时 Q.rear 的下一个位置是 Q.front，而队空时是 Q.rear == Q.front，这样就区分开了。
http://www.dtcms.com/a/484133.html

相关文章：

  • 网站设计报价方案yu网站建设
  • 如何配置php网站富阳网站建设找哪家
  • 东莞网站制作方案定制有哪些网站做汽车周边服务
  • p2p网站开发方法热门搜索
  • 投资 公司 网站模板wordpress 批量审核
  • 网站建设公司哪家好智搜宝新网的网站建设一般是多少钱
  • 天津网站建设制作开发公司怎么做企业的网站
  • Apache Doris 与 ClickHouse：运维与开源闭源对比
  • 开封旅游网站建设项目方案青岛 制作网站 大点的公司
  • 做付费网站站长全自动年赚30万app管理系统
  • 面经Java
  • 网站建设什么服务器好什么网站可以做单词书
  • 定制东莞网站制作公司查域名ip地址查询
  • 基于pycharm和anaconda的yolo简单部署测试
  • 沧州南皮手机网站建设网站后台模板论坛
  • 2014年10月自考《信息组织》试题
  • 网站哪家好百度网盘人工申诉电话
  • 【下载安装】mysql
  • 厚街镇仿做网站广州出名的网站
  • Go 语言条件语句详解
  • 中国建设部官方网站绿色建筑竞价排名深度解析
  • 把自己的网站卖给别人后对方做违法山西省建设厅官方网站
  • Bert：从“读不懂上下文”的AI，到真正理解语言
  • 成立网站要什么手续负责网站建设
  • 常州免费企业网站建设百度搜索风云榜小说
  • 产品网站建设公司官方网站内容可做证据吗
  • 2019年4月自考《信息组织》试题
  • 网站制作钱网站下拉菜单代码
  • 做公司 网站怎么在网站上做外链
  • [嵌入式系统-108]：定昌电子DC-A588电路板介绍，一款基于瑞芯微RK3588芯片的高性能嵌入式AI边缘计算工控主机