【蓝桥杯】刷题

刷题网站
记录总结刷题过程中遇到的一些问题

1、最大公约数与最小公倍数

a,b=map(int,input().split())

s=a*b

while a%b:

    a,b=b,a%b

print(b,s//b)

2.迭代法求平方根(题号1021)

#include<stdio.h>
#include<math.h>
int main()
{
    double x1=1.0,x2;
    int a;
    scanf("%d",&a);
    do
    {
        x1=x2;
        x2=(x1+a/x1)/2;
    }while(fabs(x2-x1)>0.00001);
    printf("%.3lf",x1);
    return 0;
}

3、筛选N以内的素数(1022)

采用埃筛法筛选素数

思路是给定一个较大的bool数组，刚开始将其所有元素赋值为True,从2开始，那么2的倍数就一定不是素数，将对应的bool值重新赋值为0，依次,3的倍数也不是素数…

N=int(input())
isprime=[True]*10000
isprime[0]=False
isprime[1]=False
# print(isprime[0:10])
for i in range(2,N):
    if (isprime[i]==True):
        index=i
        while index<N:
            index+=i
            isprime[index]=0
for i,val in enumerate(isprime[0:N]):
    if val==True:
        print(i)

4、求完数（1017）

一个数如果恰好等于不包含它本身所有因子之和，这个数就称为"完数"。 例如，6的因子为1、2、3，而6=1+2+3，因此6是"完数"。

① 这个题最常见的思路是两层循环，依次列举出每一个数的因子并判断

N=int(input())
x=[1]
for i in range(2,N+1):
    for j in range(2,i):
        if(i%j)==0:
            x.append(j)
    if x !=None:
        if i==sum(x):
            print("%d"%i,"its factors are ",end="")
            print(*x,sep=" ")
        x=[1]

运行时间超时了。。。。。

② 仔细思考一下，一个数的最小因子就是2（最小是2，也有可能是3、5、7），那么一个数的最大因子不会超过其1/2，所以只需要在某个数的一半找其对应的因子即可

N=int(input())
x=[1]
for i in range(2,N+1):
    for j in range(2,int(i/2)+1):
        if(i%j)==0:
            x.append(j)
    if x !=None:
        if i==sum(x):
            print("%d"%i,"its factors are ",end="")
            print(*x,sep=" ")
        x=[1]

运行时间仍然超时

分析:

第一个时间复杂度为$$n\ast n=o(n^2)$$
第二个时间复杂度为$$n\ast (\frac{n}{2})=o((\frac{n}{2}{)}^2)$$
整体时间复杂度都为
$$o(n^2)$$

③后面在网上看到了这一招，自己怎么就没想到喃，先上代码

n = int(input())
for i in range(6, n + 1, 2):
   factors = [1]
   sqrt_i = int(pow(i,0.5))
   for j in range(2, sqrt_i + 1):
       if i % j == 0:
           factors.append(j)
           if j != i // j:
               factors.append(i // j)
   if sum(factors) == i:
       print(f"{i} its factors are {' '.join(map(str, sorted(factors)))}")

其实就是先穷举找到 $$\left[0，\sqrt{x}\right]$$范围内的因子，然后用x整除这些因子，就可以求到 $$\left[\sqrt{x}，x\right]$$范围内的因子
即找全所有因子
计算复杂度可以理解为
$$o(n{\log }_{}n)$$

5、数字后移（1046）

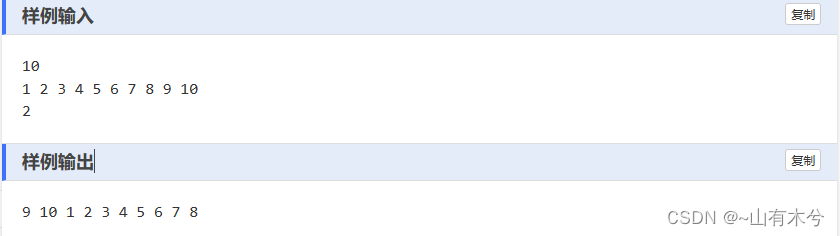
这里题目要求的是一种类似循环数组的方式，核心是取余运算

n=int(input())
x=list(input().split())
y=list(x)
m=int(input())
for i in range(0,n):
    idx=(i+m)%(n)
    y[idx]=x[i]
print(*y,sep=" ")

注意:

#指向相同的对象，x,y中的一个改变，另一个都会随之改变
x=list(input().split())
y=x
<<<<<<------------------------>>>>>>
#指向不同的对象，两个互不影响
x=list(input().split())
y=list(x)