「机器学习笔记15」深度学习全面解析:从MLP到LSTM的Python实战指南
让机器学会"看"和"听",深度学习正在重塑人工智能的边界
一、什么是深度学习?
深度学习是机器学习的一个重要分支,它通过构建多层神经网络来模拟人脑的学习过程。其核心思想是:通过层次化的特征转换,让机器自动从数据中学习复杂的特征表示。
1.1 深度学习的三大支柱
深度学习的爆发式增长得益于三个关键因素:
1. 大数据支撑
- ImageNet数据集包含1400万张标注图像
- 互联网文本数据量呈指数级增长
- 海量数据为深度网络训练提供了基础
2. 算法突破
- ReLU激活函数解决梯度消失问题
- Dropout技术防止过拟合
- Batch Normalization加速训练过程
3. 硬件革命
- GPU并行计算大幅提升训练速度
- TPU专门为神经网络优化
- 云计算降低使用门槛
1.2 深度学习 vs 传统机器学习
| 特性 | 传统机器学习 | 深度学习 |
|---|---|---|
| 特征工程 | 需要人工设计特征 | 自动学习特征 |
| 数据需求 | 相对较少 | 需要大量数据 |
| 模型复杂度 | 相对简单 | 非常复杂 |
| 可解释性 | 较好 | 较差(黑箱问题) |
二、多层感知机(MLP):神经网络的基础
2.1 MLP的基本结构
多层感知机是最基础的深度学习模型,由输入层、隐藏层和输出层组成。
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import numpy as np
import matplotlib.pyplot as plt# 创建简单的MLP模型
def create_mlp_model(input_dim, hidden_layers=[64, 32], output_dim=1):model = Sequential()# 输入层model.add(Dense(hidden_layers[0], activation='relu', input_dim=input_dim))# 隐藏层for units in hidden_layers[1:]:model.add(Dense(units, activation='relu'))# 输出层model.add(Dense(output_dim, activation='sigmoid'))return model# 示例:手写数字识别
from tensorflow.keras.datasets import mnist# 加载数据
(X_train, y_train), (X_test, y_test) = mnist.load_data()# 数据预处理
X_train = X_train.reshape(60000, 784).astype('float32') / 255
X_test = X_test.reshape(10000, 784).astype('float32') / 255# 创建MLP模型
mlp_model = create_mlp_model(input_dim=784, hidden_layers=[128, 64], output_dim=10)
mlp_model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])# 训练模型
history = mlp_model.fit(X_train, y_train, epochs=10, batch_size=32, validation_split=0.2)# 评估模型
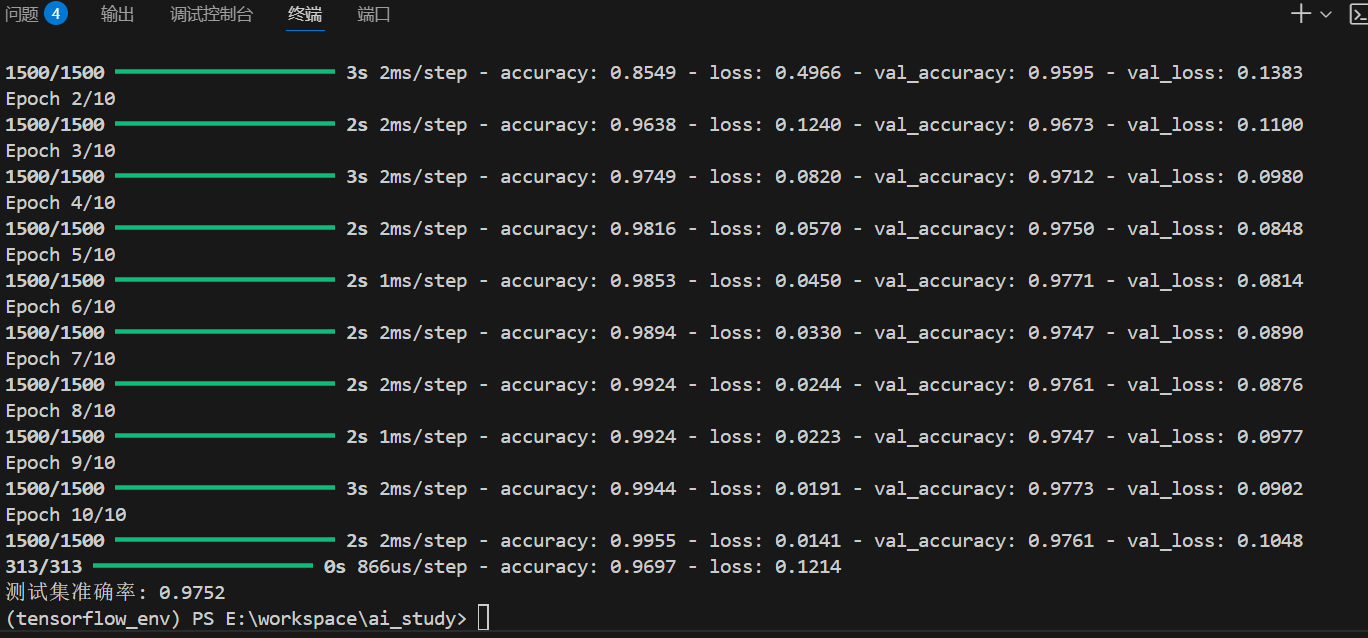
test_loss, test_accuracy = mlp_model.evaluate(X_test, y_test)
print(f"测试集准确率: {test_accuracy:.4f}")
运行结果:
2.2 激活函数:引入非线性的关键
激活函数是神经网络的灵魂,它决定了神经元的输出方式。
常用激活函数对比
import numpy as np
import matplotlib.pyplot as plt# 定义各种激活函数
def sigmoid(x):return 1 / (1 + np.exp(-x))def relu(x):return np.maximum(0, x)def tanh(x):return np.tanh(x)def leaky_relu(x, alpha=0.01):return np.where(x > 0, x, alpha * x)# 可视化激活函数
x = np.linspace(-5, 5, 100)
plt.figure(figsize=(12, 8))plt.subplot(2, 2, 1)
plt.plot(x, sigmoid(x))
plt.title('Sigmoid函数')
plt.grid(True)plt.subplot(2, 2, 2)
plt.plot(x, relu(x))
plt.title('ReLU函数')
plt.grid(True)plt.subplot(2, 2, 3)
plt.plot(x, tanh(x))
plt.title('Tanh函数')
plt.grid(True)plt.subplot(2, 2, 4)
plt.plot(x, leaky_relu(x))
plt.title('Leaky ReLU函数')
plt.grid(True)plt.tight_layout()
plt.show()
运行结果:
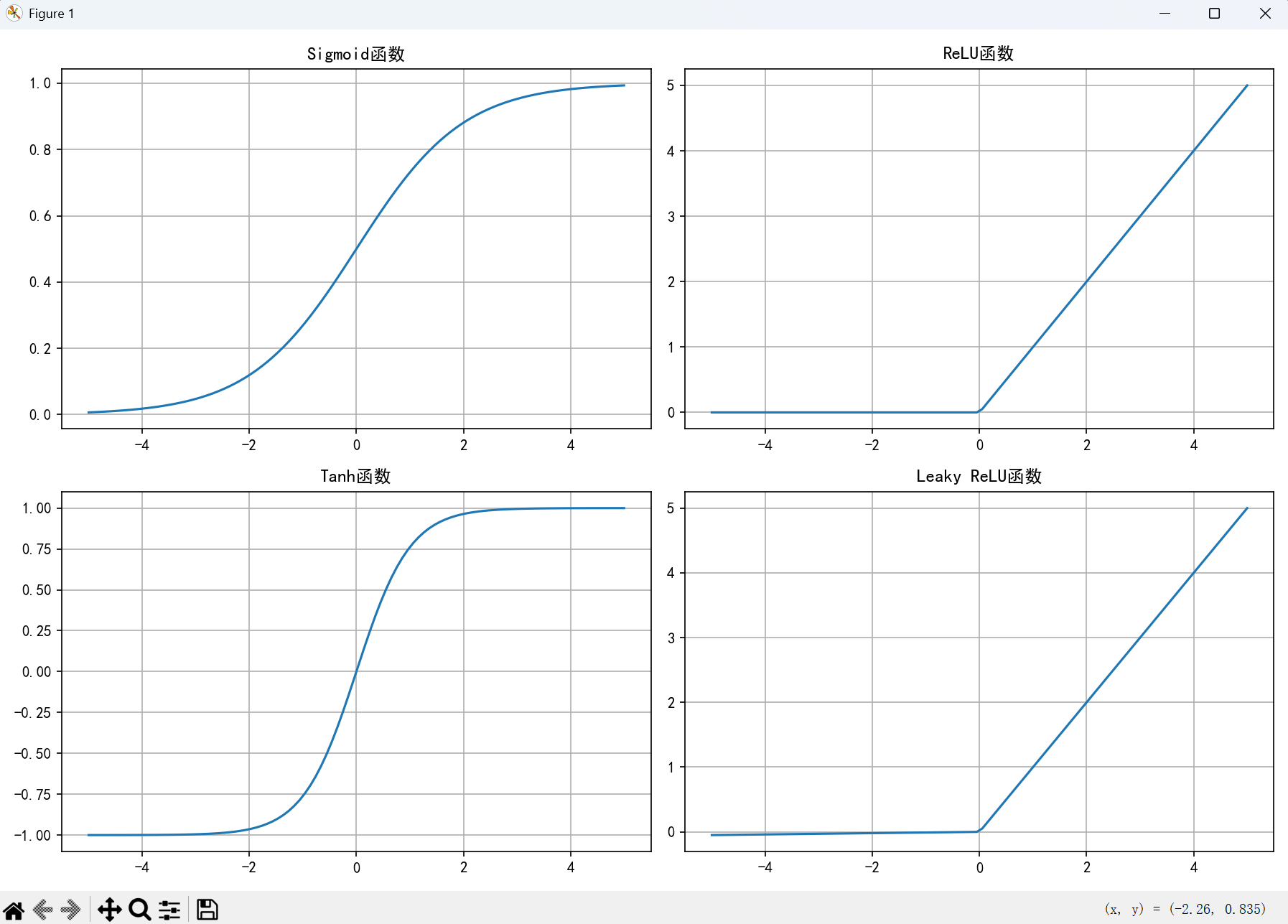
激活函数选择指南:
- ReLU:最常用,计算简单,缓解梯度消失
- Sigmoid:输出在0-1之间,适合二分类
- Tanh:输出在-1到1之间,零中心化
- Leaky ReLU:解决ReLU的"神经元死亡"问题
2.3 前向传播与反向传播
前向传播公式: z [ l ] = W [ l ] a [ l − 1 ] + b [ l ] z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]} z[l]=W[l]a[l−1]+b[l] a [ l ] = g [ l ] ( z [ l ] ) a^{[l]} = g^{[l]}(z^{[l]}) a[l]=g[l](z[l])
反向传播关键公式: ∂ L ∂ z [ l ] = ∂ L ∂ a [ l ] ⋅ g ′ [ l ] ( z [ l ] ) \frac{\partial L}{\partial z^{[l]}} = \frac{\partial L}{\partial a^{[l]}} \cdot g'^{[l]}(z^{[l]}) ∂z[l]∂L=∂a[l]∂L⋅g′[l](z
