Codeforces1058(Div.2) A至F题解

鄙人不才，只写出六道题（其他的是真不会了）。

A. MEX Partition

题面：

（翻译有点小问题，将就看吧）。

大致说一下题意：就是给你一个多重集合 $B$（其中元素允许重复），然后要你把它划分成好几块，使得每一块的 MEX 一样（MEX 是啥我就不多说了），请问在所有划分中总 MEX 最小是多少。

很明显，要让每一块的 MEX 都相同，那说明每一块中对 MEX 造成影响的数必然每一块都含有，那我们假设有一个数 $x$，总共有 $a$ 个，那全放在一起肯定不行，少放一个集合肯定也不行。所以说每个集合中都肯定有 $x$ 这个数。有多少暂且不知道，不过我们可以去重啊！去重之后每个集合内都肯定只有一个 $x$，这时你再仔细想想：每个集合中肯定都含有 $x$ 这个元素。这不是说明每个集合去重完之后不都是一样的吗？回到原数组上来：这就说明了对原数组进行排序去重之后的 MEX 其实就是每个集合唯一相同的 MEX，那答案肯定也就只能是这个 MEX 了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,a[106];
signed main()
{cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}sort(a+1,a+n+1);n=unique(a+1,a+n+1)-a-1;int k=0;for(int i=1;i<=n;i++){if(a[i]!=k){cout<<k<<'\n';break;}k++;}if(k==a[n]+1){cout<<k<<'\n';}}return 0;
}

B. Distinct Elements

题面：

其实说白了就是已知有一个 $b$ 数组的构造方式是这样的：$b_i=f(a[1,i])+f(a[2,i])+\cdots +f(a[i,i])$（其中 $f$ 表示这一段区间内不同的元素个数，$[x,y]$ 表示区间 $x\to y$，包含 $x,y$）。现在给你一个 $b$ 数组，问你 $a$ 数组的一种可行的构造方法是什么。

对于这种做和的题，我们很容易想到类似于前缀和这样的东西，也就是说我们要看看 $b_{i-1}$ 与 $b_i$ 有没有什么关系。

已知 $b_{i-1}=f(a[1,i-1])+f(a[2,i-1])+\cdots +f(a[i-1,i-1])$，那么我们来看看多了个 $a_i$ 有什么影响。

很明显，多了的 $a_i$ 肯定会对从上一个出现 $a_i$ 的地方往后的每一个位置多加一个贡献。什么意思呢？看看下面这张图就知道了：

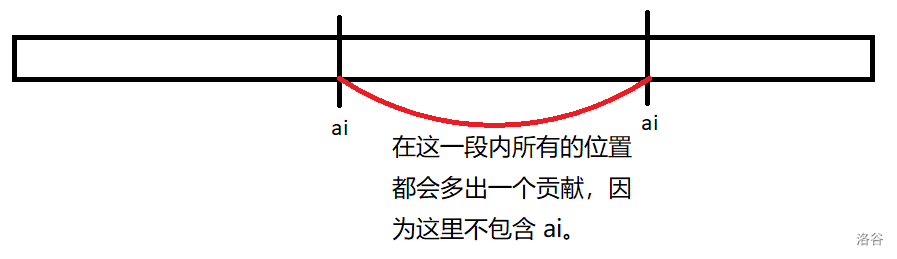
而这个多的贡献又是什么？当然是 $b_i-b_{i-1}$ 了。因此，我们可以很轻易的得出一个结论：

$a_i=a_{i-(b_i-b_{i-1})}$。

那当 $i-(b_i-b_{i-1})=0$ 时，说明这个位置的数对前面所有的数都有贡献，那就单独再多来一个数就对了。

然后就可以愉快的写代码了。

AC 代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,a[100006],b[100006];
signed main()
{cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++){cin>>b[i];}int k=1;for(int i=1;i<=n;i++){int la=i-(b[i]-b[i-1]);//算上一个位置if(la==0){a[i]=k;//单独一个数k++;}else{a[i]=a[la];}}for(int i=1;i<=n;i++){cout<<a[i]<<" ";}cout<<'\n';}return 0;
}

C. Reverse XOR

题面：

题目大意： 给你一个数，问它是否能由一个数在二进制下的数与把这个二进制数翻转过来（不是按位反转）后的数异或起来构成。

我们假设存在一个数，使得 $x\oplus f(x)=n$，那很明显，这个 $n$ 在二进制下一定是对称的。

证明：假设 $(x{)}_{10}=(\overline{a_1{a}_2\dots a_m}{)}_2$，取出其中两个数 $a_i,a_j$ 并保证 $i+j=m+1$（也就是关于中间对称），那么在倒过来之后第 $i$ 位就会变成 $a_i\oplus a_j$，而第 $j$ 位就会变成 $a_j\oplus a_i$，很明显，这两个数是相同的，因此 $n$ 一定左右对称。

然后这道题就很简单了：因为 $n$ 有可能在算完之后要去前导 $0$，所以我们就在它前面补上几个 $0$ 呗，补几个呢？容易想到，只需要补到跟最后面 $0$ 的个数一样就可以了（这样可以保持对称）。

最后要注意的一个点：如果 $n$ 在二进制下有奇数位，那最中间那一位就会异或上自己，也就是最终结果一定为 $0$，因此如果 $n$ 在二进制下有奇数位但中间那一位是 $0$，也是不成立的。

AC 代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,x,a[66];
signed main()
{cin>>t;while(t--){cin>>x;int n=0;while(x)//转二进制{a[++n]=x&1;x>>=1;}int sum=0;for(int i=1;i<=n;i++){if(a[i]){break;}sum++;}for(int i=n+1;i<=n+sum;i++)//补 0{a[i]=0;}n+=sum;bool fl=true;for(int i=1;i<=n/2;i++){if(a[i]!=a[n-i+1]){fl=false;}}if(n&1){cout<<((fl&&a[n/2+1]==0)?"YES":"NO")<<'\n';}else{cout<<(fl?"YES":"NO")<<'\n';}}return 0;
}

D. MAD Interactive Problem

题面：

对于互动加构造题，它们都有一个很通俗的做法：研究题目给的条件的性质。关于这个 MAD 我就不多说了。我们来思考这个 MAD 有什么用。

注意题目中写了：每个数恰好出现两次。因此如果我们随便选两个数去测，测出来是一个非零的数，那这两个数肯定都是返回的这个值了。这样做肯定可以，不过最坏情况下是 $n+(n-2)+(n-4)+\cdots +0$ 次的，稍微算一下就会发现当 $n$ 很大时这种方法明显过不了。

现在假设我们就选了 $a_1,a_2$ 来测，并且返回值就是一个 0，这能说明什么？说明 $a_1\ne a_2$。现在我们来多测一个 $a_3$，那如果返回值是一个 $x(x\ne 0)$，这能很明显的说明一点：$a_3=x$。因为没 $a_3$ 就是 0，有了 $a_3$ 就是 $x$，那 $a_3$ 不是 $x$ 还能是几。

那我们都知道 $a_3$ 的值是多少了，那把它拿来测也没用，反而可能会影响判断（因为 MAD 返回的是最大值），所以我们直接把 $a_3$ 丢掉。

假设 $a_1,a_2,a_3$ 测出来还是 0，那我们继续测 $a_4$，与上面同理，我们有可能能确定 $a_4$ 的值，也有可能不确定。

最终，通过 $2n$ 次查询，我们就能确定其中的 $n$ 个数的值。

现在我们来考虑如何用 $n$ 次机会算出剩下 $n$ 个数。

$n$ 次机会 $n$ 个数，明显一个数一次机会，那我们就沿用上面的结论：把 $1\to n$ 所有的数放一起跟 $a_i$ 测，测出来是多少 $a_i$ 就是多少。这样正好每个数测一次，一共 $3n$ 次。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,a[606];
int query(int x,vector<int>v)
{cout<<"? "<<v.size()+1<<" ";cout<<x<<" ";for(auto i:v){cout<<i<<" ";}cout<<endl;int y;cin>>y;return y;
}
signed main()
{cin>>t;while(t--){cin>>n;vector<int>v;v.push_back(1);for(int i=2;i<=n*2;i++){int x=query(i,v);//先测出 n 个数if(x){a[i]=x;}else{v.push_back(i);}}v.clear();for(int i=1;i<=n*2;i++){if(a[i]){v.push_back(i);}}for(int i=1;i<=n*2;i++)//再拿这 n 个数去测其他的数{if(a[i]){continue;}a[i]=query(i,v);}cout<<"! ";for(int i=1;i<=n*2;i++){cout<<a[i]<<" ";a[i]=0;}cout<<endl;}return 0;
}

E. Rectangles

题面：

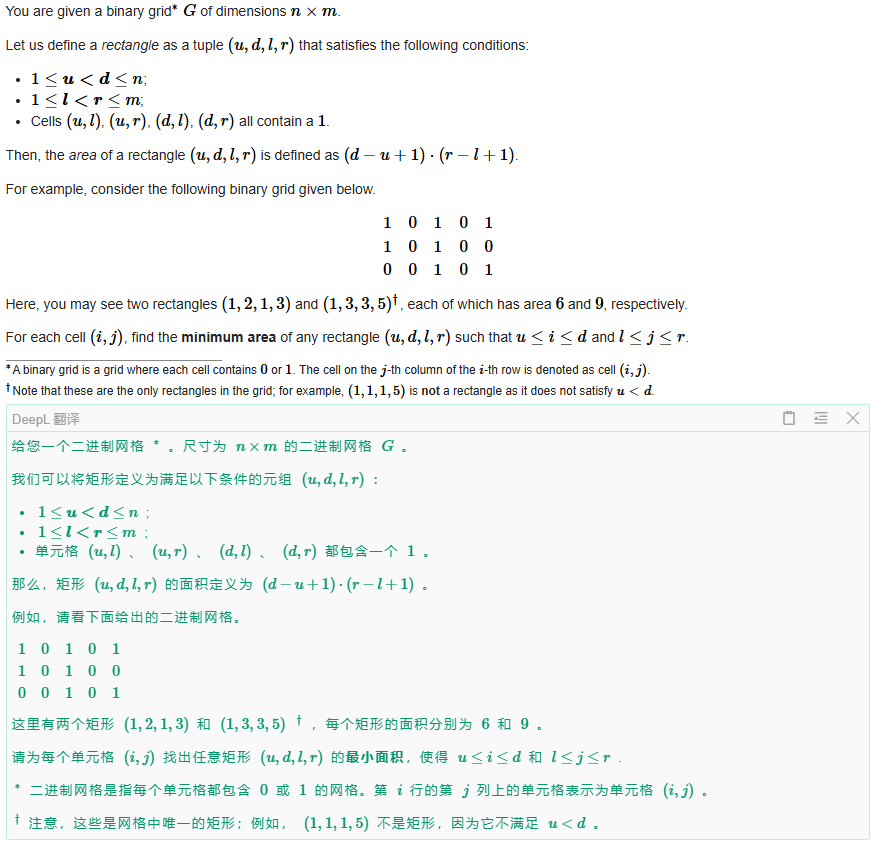
其实简化一下，就是说对于每个格子，你要找到一个矩阵满足四个角都是 1 且包含这个格子，那么这个格子的值就是所有满足上述条件的矩阵大小中的最小值。

首先我们不难想到一个 $O(n^3{m}^3)$ 的做法：枚举上下左右的边界，然后看看是否满足条件，如果满足，直接枚举中间每一个格子，然后更新答案，最坏情况下 $O(n^3{m}^3)$。

如果你稍微思考了一下你就会发现：其实左右界根本不需要都枚举，因为最优解一定是上一个满足条件的列与当前这一满足条件的列组成的矩阵，不可能跨两个矩阵，这样显然不是更优的。这样，时间复杂度就到了 $O(n^3{m}^2)$。

如果你再进一步想，你就可以想到：我们可以把当前算出来的最小值保存在某一行上，到最后再更新其他的位置。那恭喜你，你已经想到了 $O(n^{2}m)$ 的做法了。其实我们只需要每次在矩阵最下面赋值为最小情况，在每次确定了上界并算完了之后做后缀最小值就可以求出答案。

最后一个问题：$n\le 250000$，在最坏情况下时间复杂度可能达到 $62500000000$，这时如果你再 gou 一点，你就会这样想：把 $n$ 换成 $\min (n,m)$ 不就行了，于是你就会选择行和列中更短的那个来枚举边界，时间复杂度会变成 $\min (n,m{)}^2\max (n,m)$，因为 $\min (n,m)\le \sqrt{nm}=500$，所以最坏情况下时间复杂度大概是 $125000000$，差不多用时 1s 多一点，时限 4s，能过！

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,m;
vector<vector<int>>v;
vector<vector<int>>ans;
signed main()
{cin>>t;while(t--){cin>>n>>m;v=vector<vector<int>>(n+6,vector<int>(m+6,0));ans=vector<vector<int>>(n+6,vector<int>(m+6,LONG_LONG_MAX));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){char c;cin>>c;v[i][j]=c-'0';}}if(n<m)//gou{for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){int la=0;for(int k=1;k<=m;k++){if(v[i][k]&&v[j][k]){if(la){for(int l=la;l<=k;l++){ans[j][l]=min(ans[j][l],(j-i+1)*(k-la+1));}}la=k;}}}for(int j=n-1;j>=i;j--){for(int k=1;k<=m;k++){ans[j][k]=min(ans[j][k],ans[j+1][k]);}}}}else{for(int i=1;i<=m;i++){for(int j=i+1;j<=m;j++){int la=0;for(int k=1;k<=n;k++){if(v[k][i]&&v[k][j]){if(la){for(int l=la;l<=k;l++){ans[l][j]=min(ans[l][j],(j-i+1)*(k-la+1));}}la=k;}}}for(int j=m-1;j>=i;j--){for(int k=1;k<=n;k++){ans[k][j]=min(ans[k][j],ans[k][j+1]);}}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cout<<(ans[i][j]==LONG_LONG_MAX?0:ans[i][j])<<" ";}cout<<'\n';}}return 0;
}

F. Twin Polynomials

题面：

对于这种从一类变换到另一类的题让我想起了之前的从一个字符串变到另一个字符串那道题，当时那道题的正解是建图，所以这里我们也先建个图看看。

其中对于每个节点，用 $(x,y)$ 来表示，第一位表示系数，第二位表示指数。

那么我们就可以得到这样一个连边关系：$(x,y)\to (y,x)$，同时 $(y,x)\to (x,y)$。因此我们得到了第一条非常重要的性质：$a_{a_i}=i$，即我的系数变成指数后的系数应该是我的指数。或者说是 $-1$，这样可以变成 $i$。

那有没有一种可能：我的两项变换后的两个指数一样，而系数却不同呢（在这种情况下就违背了上面我们得出的结论）？这是不可能的，证明如下：

证明：如果存在两个节点 $(x,y)$ 与 $(x,z)$，在变换之后应该是 $(y,x)$ 和 $(z,x)$，在多项式里面就是 $(y+z){a_x}^x$，也就是说我们把其中的两项变成了一项！但我们又要保证新的多项式与原多项式一样，所以这里明显矛盾，所以不成立。

因此我们就得到了第二条性质：不存在两个点同时连到一个点的情况。这里要特殊说明一下，就是如果变换后指向了第一位为 0 的点，那这没有什么关系，因为系数为 0 代表着什么都没有，也就不会违背上面的规则了。

在上面一通操作之后，我们肯定还剩一些没法确定的点，那这些点我们就统计起来，记作 $cnt$，并设一个 $d{p}_i$ 表示有 $i$ 个不确定的点时的方案数是多少。首先，这些不确定的点肯定能连到第一位是 $0$ 的点上，这时这个点对其他不确定的点并没有什么影响，所以总方案数加一个 $d{p}_{i-1}$；其次就是可以形成自环，这样也不会对其他点有什么影响，也是 $d{p}_{i-1}$；最后就是它跟其中一个不确定的点互相连上了，这时有 $i-1$ 个点可以选，选完之后还剩下 $i-2$ 个点，共 $d{p}_{i-2}$ 种方案，所以方案数再加一个 $(i-1)d{p}_{i-2}$。最后输出 $d{p}_{cnt}$ 就行了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,a[400006],dp[400006];
const int mod=1e9+7;
int read()
{int z=0,f=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}while(c>='0'&&c<='9'){z=z*10+c-'0';c=getchar();}return z*f;
}
void write(int x)
{if(x<0){putchar('-');x=-x;}static int top=0,stk[106];while(x){stk[++top]=x%10;x/=10;}if(!top){stk[++top]=0;}while(top){putchar(char(stk[top--]+'0'));}
}
signed main()
{cin>>t;PO://一种类似于 while 的方法t--;n=read();for(int i=0;i<=n;i++){a[i]=read();}for(int i=1;i<=n;i++){if(a[i]<=0){continue;}if(a[i]>n||a[a[i]]!=-1&&a[a[i]]!=i)//如果不满足性质{puts("0");if(!t){return 0;}goto PO;}a[a[i]]=i;}int cnt=0;for(int i=1;i<=n;i++){if(a[i]==-1)//统计 -1 的个数{cnt++;}}dp[0]=1;for(int i=1;i<=cnt;i++)//DP 转移{dp[i]=2*dp[i-1]%mod;if(i>1){dp[i]=(dp[i]+dp[i-2]*(i-1)%mod)%mod;}}write((dp[cnt]+(a[n]==-1?mod-dp[cnt-1]:0))%mod);putchar('\n');for(int i=1;i<=cnt;i++){dp[i]=0;}if(!t){return 0;}goto PO;
}