使用Mathematica做Lorenz系统的稳定性分析

Lorenz-Haken系统（通常简称Lorenz系统）是混沌理论和非线性动力学中的一个经典模型。使用Mathematica分析其稳定性主要涉及​​寻找平衡点​​、​​计算雅可比矩阵​​、​​分析特征值​​，以及运用​​Lyapunov稳定性理论​​等方法。

1. 定义Lorenz-Haken方程

首先，我们定义Lorenz-Haken方程。该系统通常用于模拟对流等现象，其方程如下：

(*定义系统参数和微分方程*)
sigma = 10; (*Prandtl数*)
rho = 28;   (*瑞利数*)
beta = 8/3; (*几何因子*)(*定义Lorenz方程*)
lorenzEq = {x'[t] == sigma (y[t] - x[t]),y'[t] == x[t] (rho - z[t]) - y[t],z'[t] == x[t] y[t] - beta z[t]};

2.  寻找平衡点

平衡点是系统状态不再随时间变化的点，即导数为零的点。

(*求解平衡点*)
equilibriumPoints = Solve[{sigma (y - x) == 0, x (rho - z) - y == 0, x y - beta z == 0}, {x, y, z}, Reals]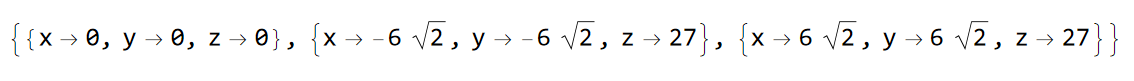

3. 计算雅可比矩阵与特征值

雅可比矩阵描述了系统在平衡点附近的线性化行