【前缀和】| LeetCode 1314题解 矩阵区域和

一、题目链接

矩阵区域和

二、题目

三、算法原理

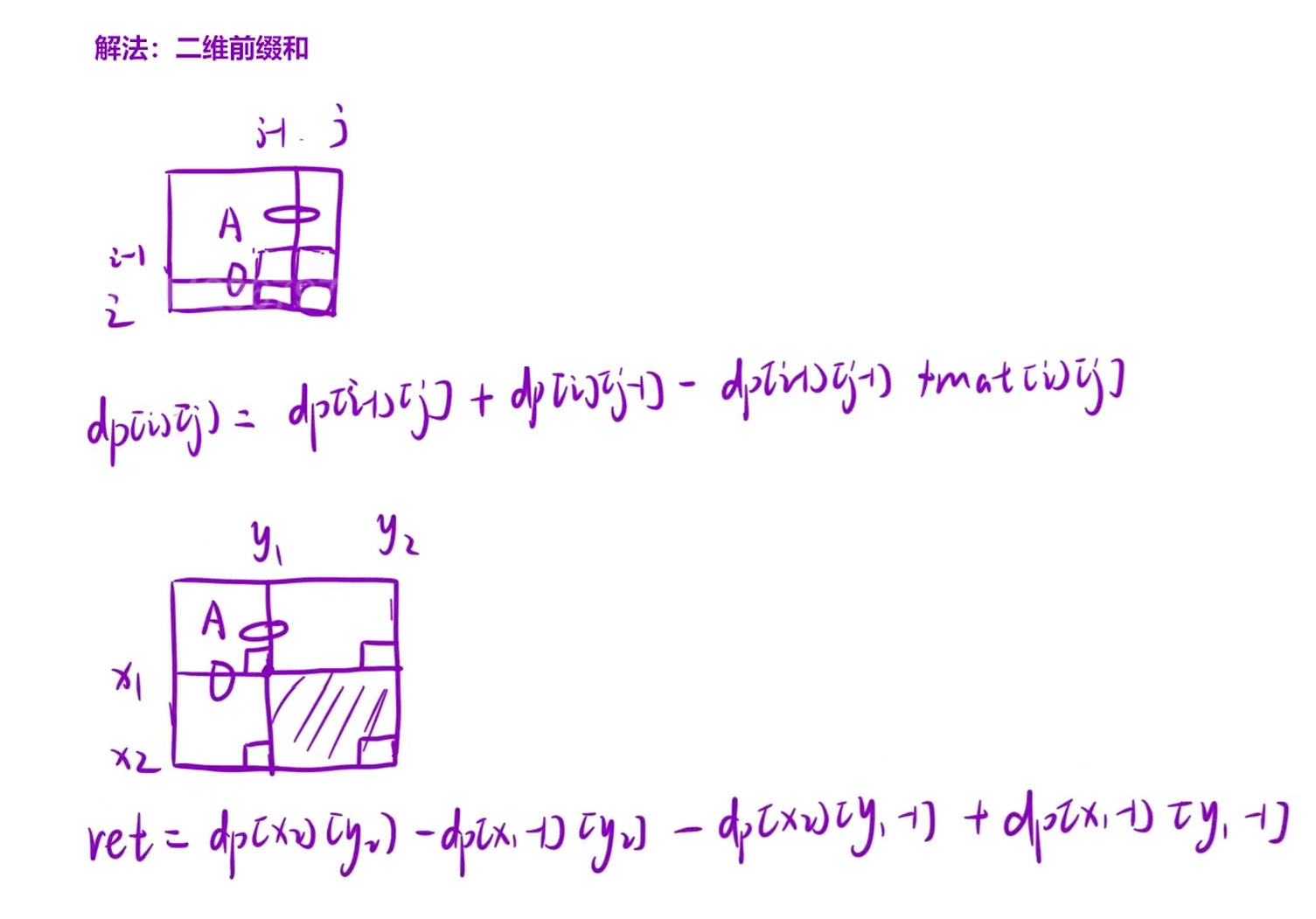
二维前缀和的应用：answer里的任一元素的值等于mat对应元素上下左右扩展k个单位所围成的矩阵里的所有元素之和。若超出了矩阵的范围，则超出范围忽略不计。

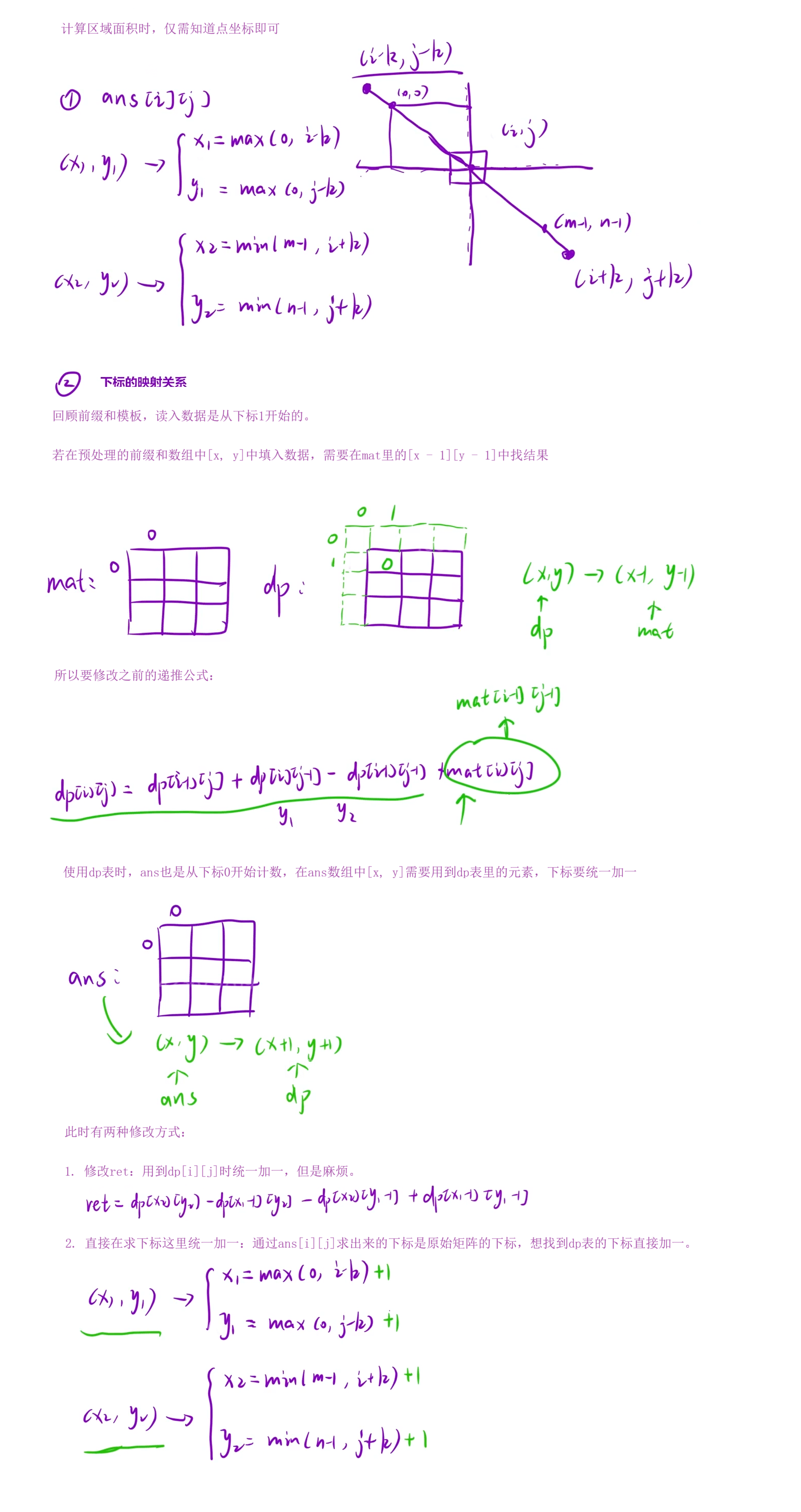
四、编写代码

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();// 1.预处理一个前缀和矩阵vector<vector<int>> dp(m + 1, vector<int>(n + 1));for (int i = 1; i <= m; ++i)for (int j = 1; j <= n; ++j)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];// 2.使用vector<vector<int>> ret(m, vector<int>(n));for (int i = 0; i < m; ++i)for (int j = 0; j < n; ++j){int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];}return ret;}
};

时间复杂度是 O(m×n)，空间复杂度是 O(m×n)