二叉树的深搜

二叉树的深搜
深度优先遍历(DFS,全称为 Depth First Traversal),是树或者图这类数据结构中常用的一种遍历算法。该算法会尽可能深地搜索树或者图的分支,直到一条路径上的所有节点都被遍历完毕,之后再回溯到上一层,继续找下一条路遍历。
在二叉树里,常见的深度优先遍历有前序遍历、中序遍历以及后序遍历。由于树的定义本身是递归定义的,所以采用递归的方法去实现树的这三种遍历,不仅容易理解,代码也很简洁。而且前、中、后序这三种遍历的唯一区别就在于访问根节点的时机不同,在解题时,选择合适的遍历顺序,对理解算法是很有帮助的。
二叉树的深度优先搜索(DFS)核心是 “优先遍历当前节点的子树,再回溯处理其他分支”,对应的题目类型本质是需要 “深入挖掘节点与子树关系” 的问题—— 凡是涉及 “遍历所有节点并处理节点信息”“判断树的结构特征”“从节点向子树传递状态 / 收集结果”“在树中寻找满足条件的路径或节点” 的场景,都适合用二叉树 DFS 解决,具体可归为 4 大类:
-
全节点遍历与信息收集类:需要访问树中所有节点,并基于节点值做统计、计算或数据整理,比如 “统计二叉树中叶子节点的数量”“计算二叉树所有节点值的和”“将二叉树的节点值按前 / 中 / 后序存入数组”“找出二叉树中的所有偶数节点”,这类问题用 DFS 能自然贴合 “遍历 - 处理 - 递归子树” 的流程,无需额外维护复杂队列(区别于 BFS);
-
树的结构与属性判断类:需要验证二叉树是否满足特定结构特征,这类问题的核心是 “通过递归对比当前节点与子树的状态”,比如 “判断一棵二叉树是否为平衡二叉树(左右子树高度差不超过 1)”“判断是否为对称二叉树(左右子树镜像对称)”“判断是否为完全二叉树(按层遍历无跳跃,但 DFS 可通过节点存在性递归判断)”“判断两棵二叉树是否相同”,DFS 能通过递归深入到最底层节点,逐层验证条件是否成立;
-
路径搜索与目标查找类:需要在树中寻找满足条件的路径(从根到叶、从叶到根或任意节点间),或定位特定节点,比如 “寻找二叉树中所有和为目标值的根到叶路径”“找出二叉树中距离目标节点最近的祖先节点”“在二叉树中搜索值为 target 的节点并返回其位置”“求二叉树的最大路径和(路径可从任意节点出发到任意节点)”,DFS 的 “回溯特性” 能在探索完一条路径后回退,继续探索其他分支,高效覆盖所有可能路径;
-
树的修改与构造类:需要基于原二叉树的结构生成新树,或修改原树节点,核心是 “递归处理当前节点,再基于子树结果构造新节点 / 修改状态”,比如 “将二叉树转换为它的镜像(交换每个节点的左右子树)”“根据前序和中序遍历序列构造二叉树”“将二叉搜索树转换为累加树(每个节点值变为原树中大于等于该节点值的和)”“修剪二叉搜索树(移除所有值不在 [L,R] 范围内的节点)”,DFS 能递归到子树最底层,再从下往上或从上往下完成构造 / 修改逻辑。
题目练习
2331. 计算布尔二叉树的值 - 力扣(LeetCode)
解法(递归):
算法思路:
本题可解释为:
对于规模为 n 的问题,需要求得当前节点值。
节点值不为 0 或 1 时,规模为 n 的问题可拆分为规模为 \(n - 1\) 的子问题:
-
a. 所有子节点的值;
-
b. 通过子节点的值运算出当前节点值。
当问题规模变为 n = 1 时,即叶子节点的值为 0 或 1,可直接获取当前节点值为 0 或 1。
算法流程:
递归函数设计:bool evaluateTree(TreeNode* root)
-
返回值:当前节点值;
-
参数:当前节点指针;
-
函数作用:求得当前节点通过逻辑运算符得出的值。
递归函数流程:
-
当前问题规模为 \(n = 1\) 时,即叶子节点,直接返回当前节点值;
-
递归求得左右子节点的值;
-
通过判断当前节点的逻辑运算符,计算左右子节点值运算得出的结果。
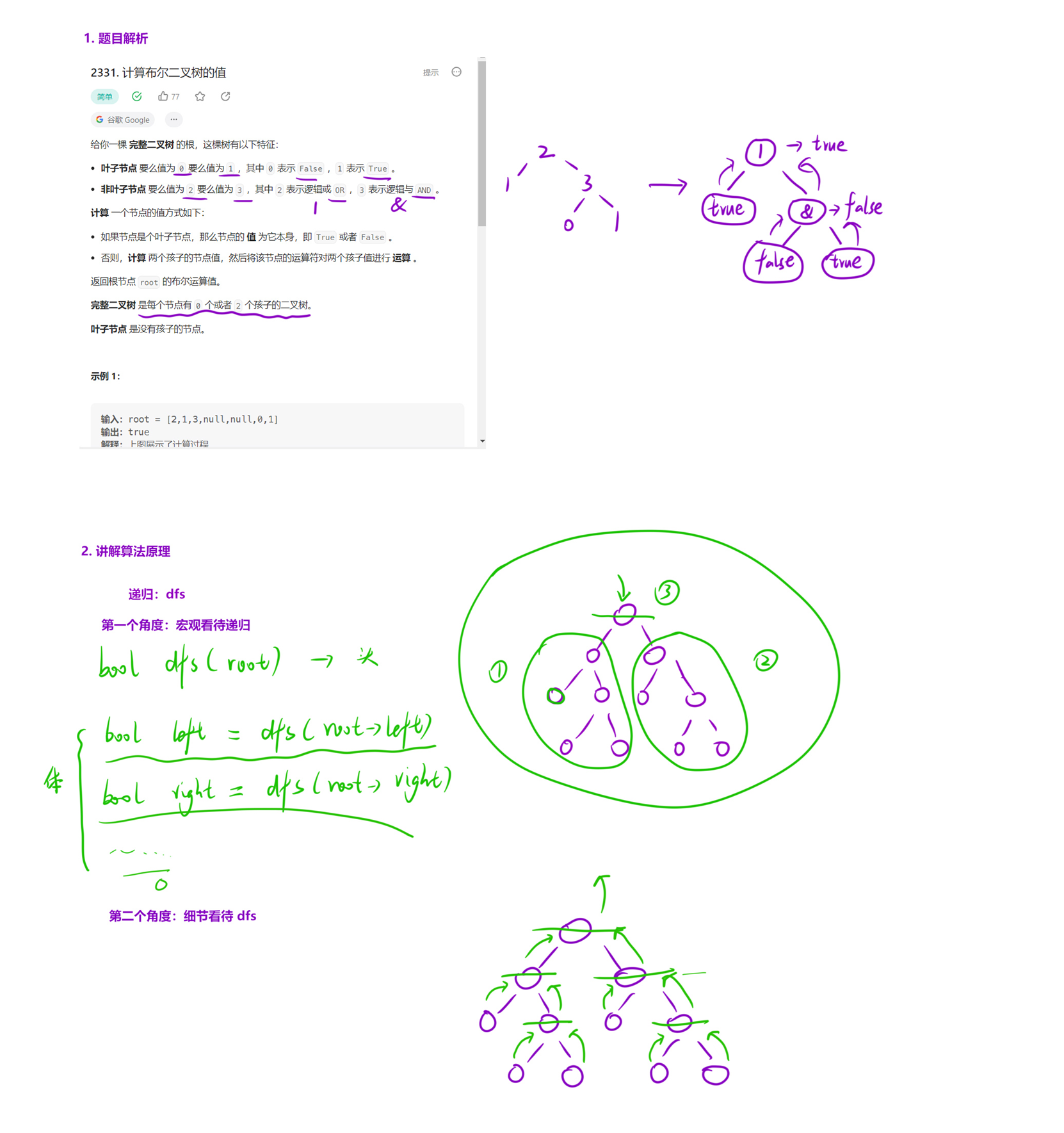
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr) return root->val;bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left | right : left & right;}
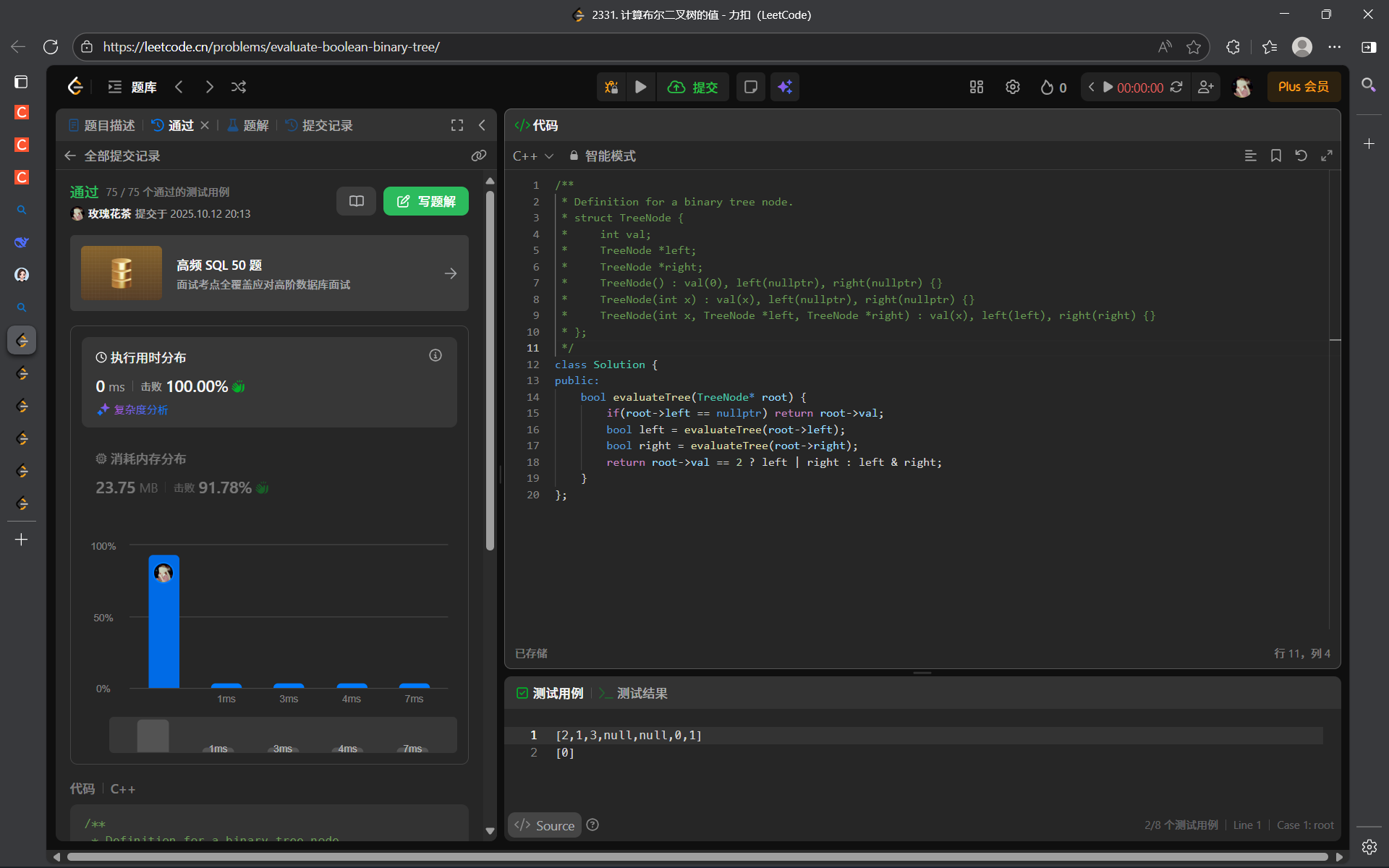
};
129. 求根节点到叶节点数字之和 - 力扣(LeetCode)
解法(dfs - 前序遍历):
算法思路:
前序遍历按照根节点、左子树、右子树的顺序遍历二叉树的所有节点,通常用于子节点的状态依赖于父节点状态的题目。
在前序遍历的过程中,我们可以往左右子树传递信息,并且在回溯时得到左右子树的返回值。递归函数可以帮我们完成两件事:
-
将父节点的数字与当前节点的信息整合到一起,计算出当前节点的数字,然后传递到下一层进行递归;
-
当遇到叶子节点的时候,就不再向下传递信息,而是将整合的结果向上一直回溯到根节点。
在递归结束时,根节点需要返回的值也就被更新为了整棵树的数字和。
算法流程:
递归函数设计:int dfs(TreeNode* root, int num)
-
返回值:当前子树计算的结果(数字和);
-
参数
num:递归过程中往下传递的信息(父节点的数字); -
函数作用:整合父节点的信息与当前节点的信息计算当前节点数字,并向下传递,在回溯时返回当前子树(当前节点作为子树根节点)数字和。
递归函数流程:
- 当遇到空节点的时候,说明这条路从根节点开始没有分支,返回
0; - 结合父节点传下的信息以及当前节点的
val,计算出当前节点数字sum; - 如果当前结点是叶子节点,直接返回整合后的结果
sum; - 如果当前结点不是叶子节点,将
sum传到左右子树中去,得到左右子树中节点路径的数字和,然后相加后返回结果。
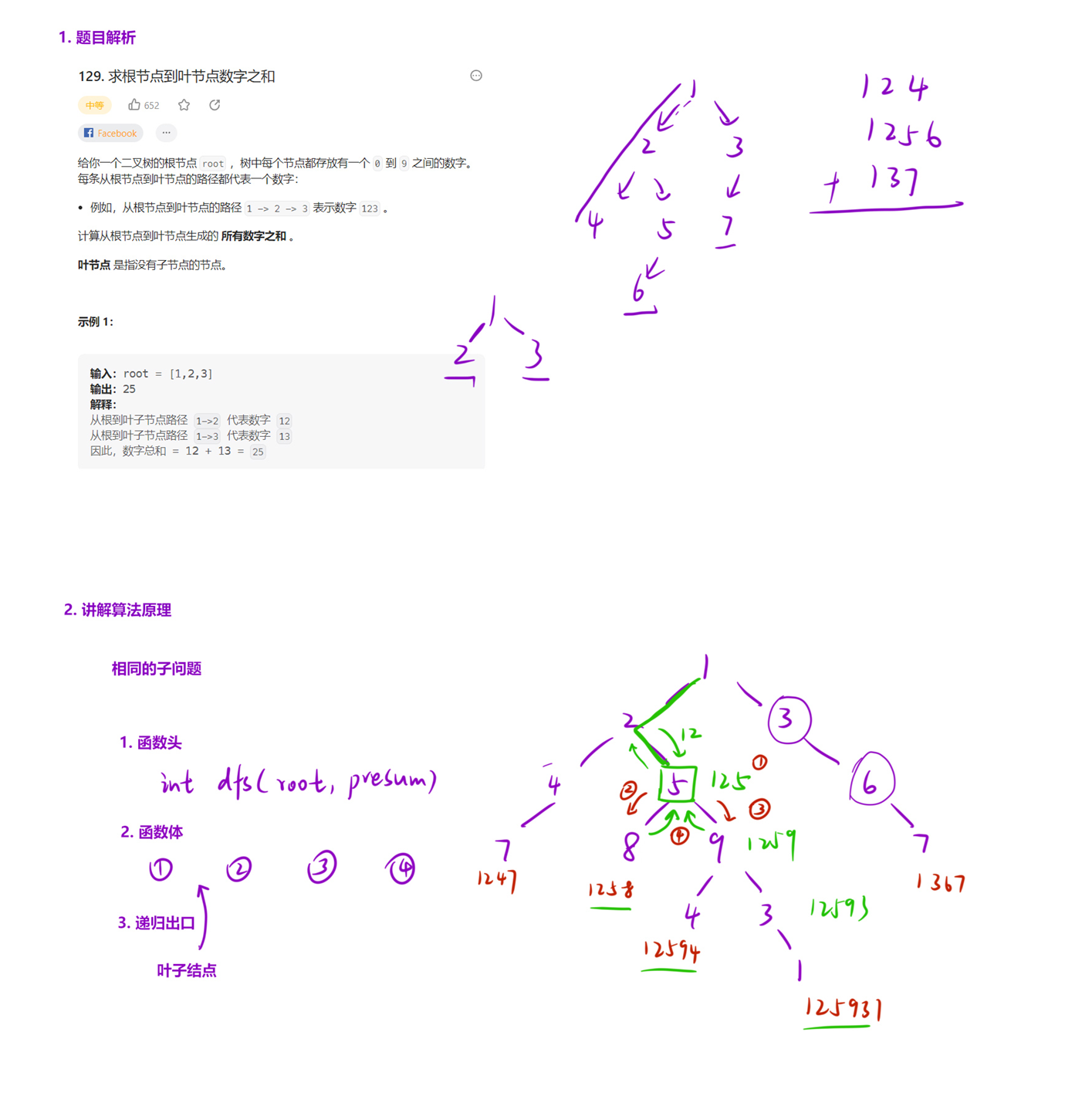
class Solution {
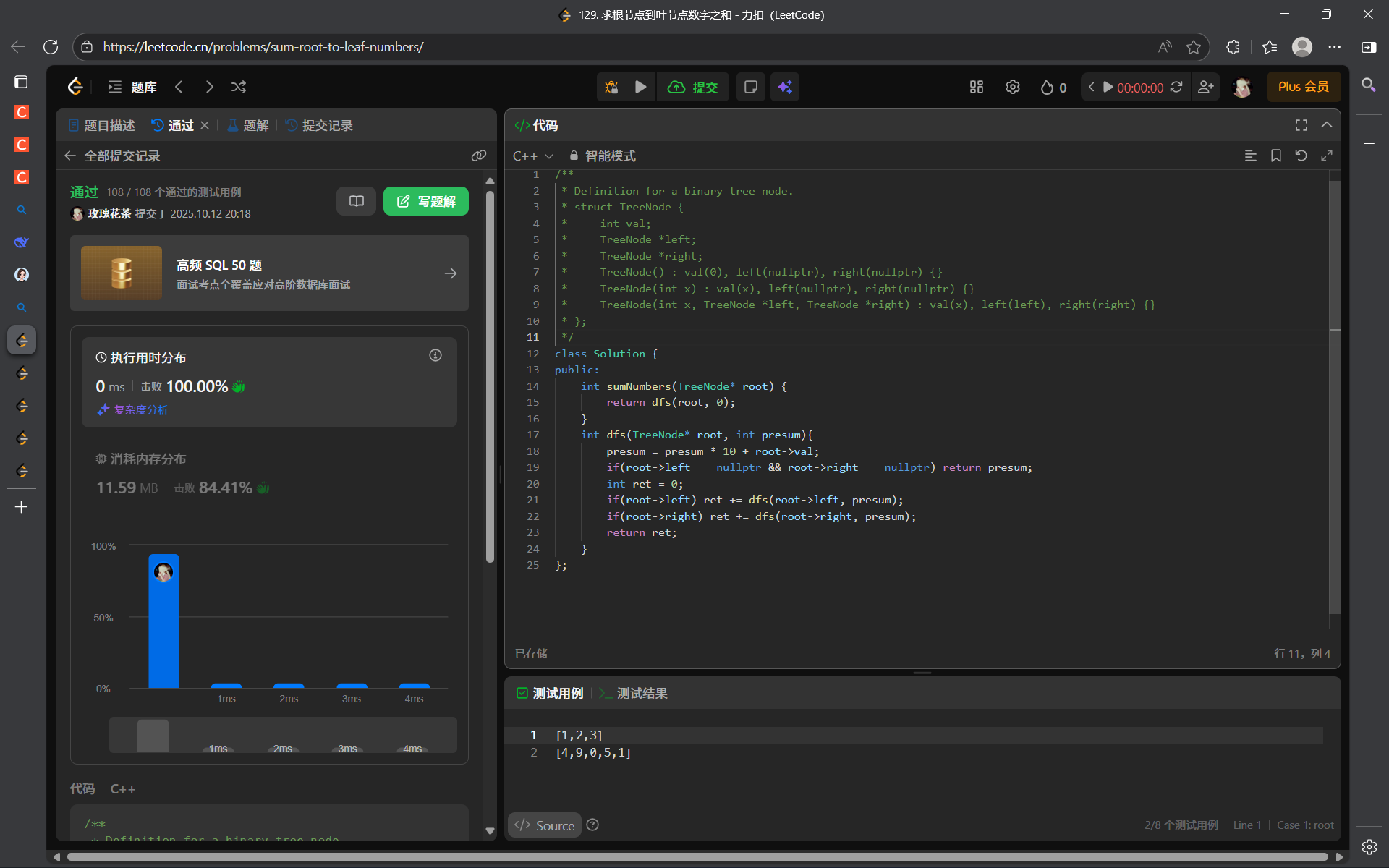
public:int sumNumbers(TreeNode* root) {return dfs(root, 0);}int dfs(TreeNode* root, int presum){presum = presum * 10 + root->val;if(root->left == nullptr && root->right == nullptr) return presum;int ret = 0;if(root->left) ret += dfs(root->left, presum); if(root->right) ret += dfs(root->right, presum); return ret;}
};
814. 二叉树剪枝 - 力扣(LeetCode)
解法(dfs - 后序遍历):
算法思路:
后序遍历按照左子树、右子树、根节点的顺序遍历二叉树的所有节点,通常用于父节点的状态依赖于子节点状态的题目。
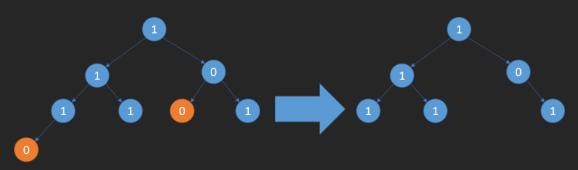
如果从上往下删除,需收集左右子树信息,代码编写相对困难。但观察发现,先删除最底部的叶子节点,再处理删除后的节点,最终结果不受影响。
所以采用后序遍历解决问题,后序遍历先处理左子树,再处理右子树,最后处理当前节点。处理当前节点时,判断其是否为叶子节点且值为 0,若满足则删除。
需要注意,删除叶子节点时,其父节点可能成为新的叶子节点,处理完子节点后仍需处理当前节点,这也是选择后序遍历的原因(后序遍历首先遍历到的一定是叶子节点)。
通过后序遍历,可逐步删除叶子节点,保证删除后的节点仍满足删除操作要求,方便实现删除操作且不影响最终结果。若处理结束后所有叶子节点值均为 1,则所有子树均包含 1,可返回。
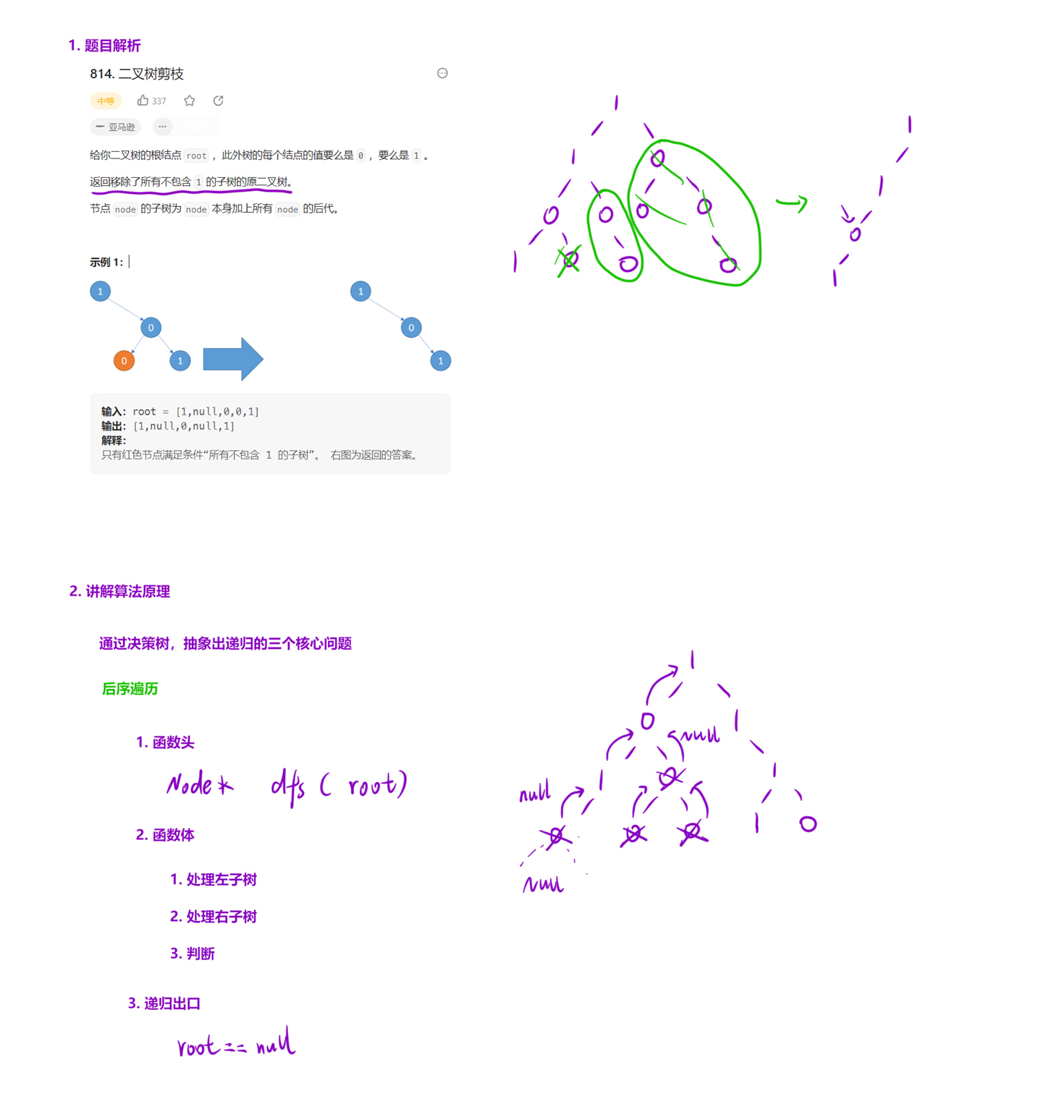
算法流程:
递归函数设计:void dfs(TreeNode*& root)
-
返回值:无;
-
参数:当前需要处理的节点;
-
函数作用:判断当前节点是否需要删除,若需要删除,则删除当前节点。
后序遍历的主要流程:
递归出口:当传入节点为空时,不做任何处理;
递归处理左子树;
递归处理右子树;
处理当前节点:判断该节点是否为叶子节点(即左右子节点均被删除,当前节点成为叶子节点),并且节点的值为 0:
- a. 如果是,就删除掉;
- b. 如果不是,就不做任何处理。
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr) return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(root->left == nullptr && root->right == nullptr && root->val == 0){// delete root; -- 这个要不要进行delete,平台应该是自动有释放,不然造成二次释放了// 还有就是可能不是 new 出来的,就好比是从 vector 中取出来的,进行&了!root = nullptr;}return root;}
};
98. 验证二叉搜索树 - 力扣(LeetCode)
解法(利用中序遍历):
算法思路:
后序遍历按照左子树、根节点、右子树的顺序遍历二叉树的所有节点,通常用于二叉搜索树相关题目。
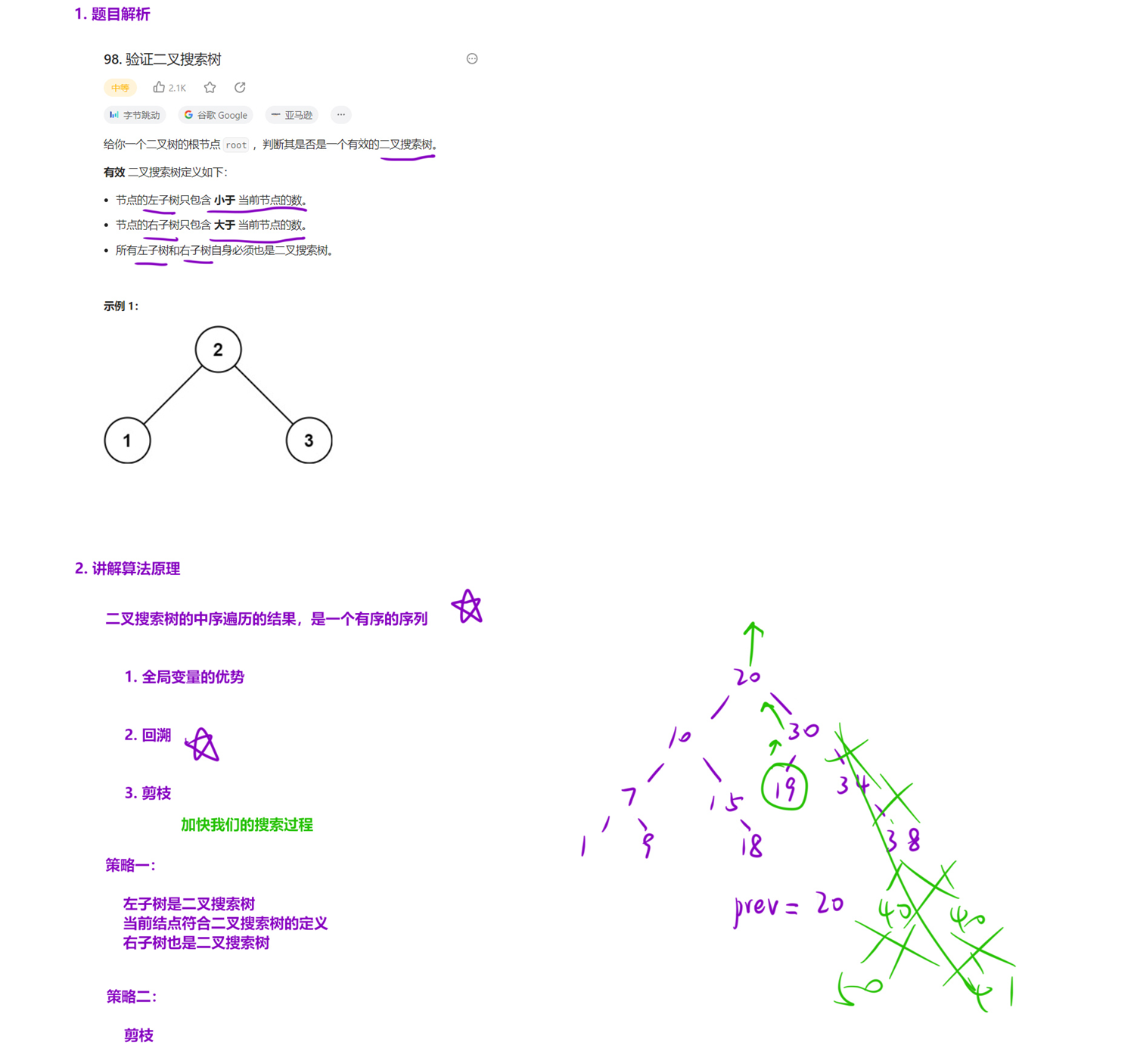
如果一棵树是二叉搜索树,那么它的中序遍历的结果一定是一个严格递增的序列。
因此,我们可以初始化一个无穷小的全局变量,用来记录中序遍历过程中的前驱结点。那么就可以在中序遍历的过程中,先判断是否和前驱结点构成递增序列,然后修改前驱结点为当前结点,传入下一层的递归中。
算法流程:
初始化一个全局的变量 prev,用来记录中序遍历过程中的前驱结点的 val;
中序遍历的递归函数中:
a. 设置递归出口:root == nullptr 的时候,返回 true;
b. 先递归判断左子树是否是二叉搜索树,用 retleft 标记;
c. 然后判断当前结点是否满足二叉搜索树的性质,用 retcur 标记:
- 如果当前结点的
val大于prev,说明满足条件,retcur改为true; - 如果当前结点的
val小于等于prev,说明不满足条件,retcur改为false;
d. 最后递归判断右子树是否是二叉搜索树,用 retright 标记;
只有当 retleft、retcur 和 retright 都是 true 的时候,才返回 true。
class Solution {
public:long long prev = LONG_MIN;bool isValidBST(TreeNode* root) {if(root == nullptr) return true;bool left = isValidBST(root->left);if(!left) return false;// 剪枝bool cur = false;if(prev < root->val){cur = true;prev = root->val;}if(!cur) return false;// 剪枝bool right = isValidBST(root->right);return left && right && cur;}
};
230. 二叉搜索树中第 K 小的元素 - 力扣(LeetCode)
其实通过中序遍历的性质知道是有序的,但是这样的空间消耗比较大!
解法(中序遍历 + 计数器剪枝):
算法思路:
上述解法不仅使用大量额外空间存储数据,并且会将所有的结点都遍历一遍。
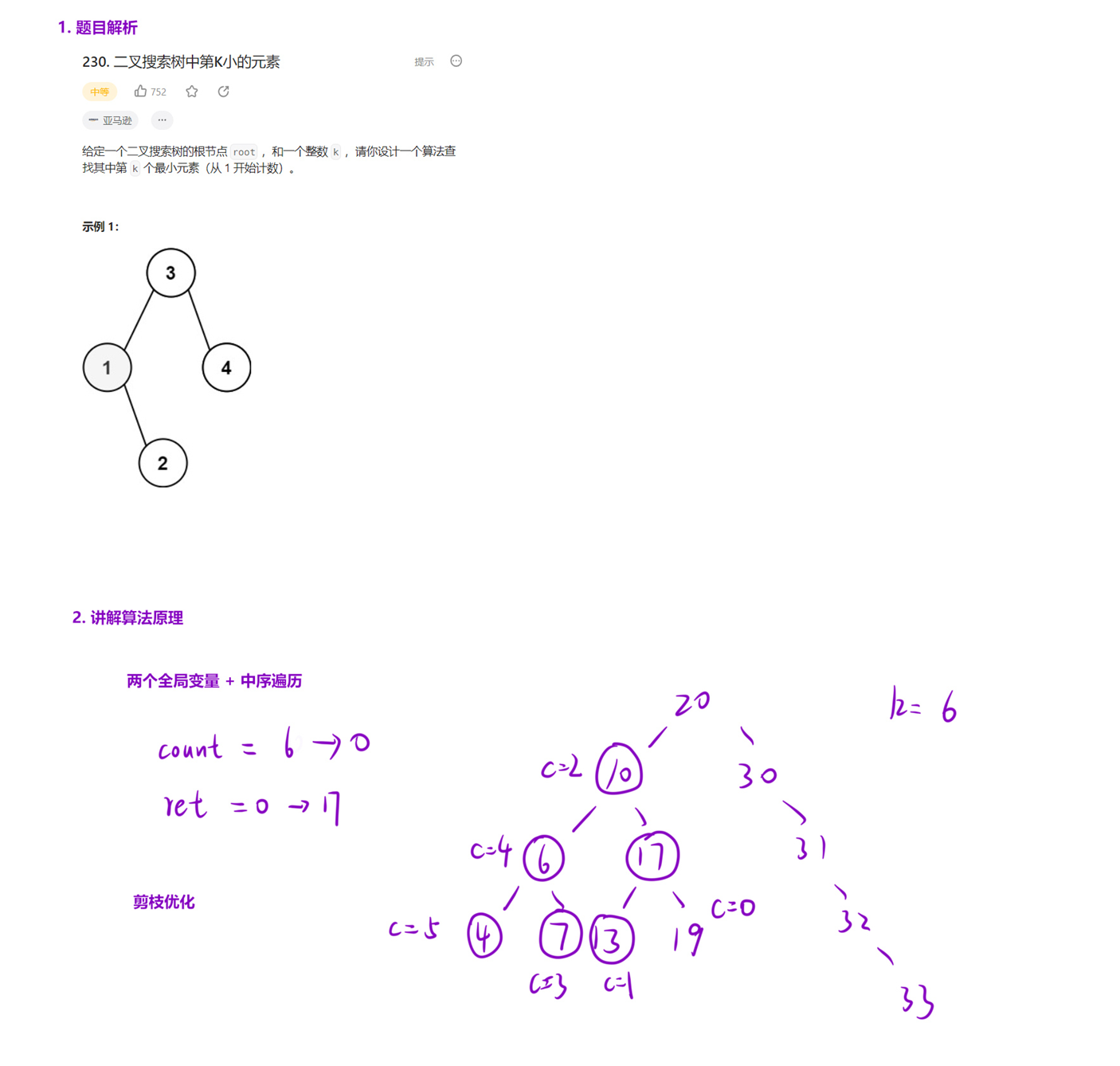
但我们可以根据中序遍历的过程,只需扫描前 k 个结点即可。
因此,我们可以创建一个全局的计数器 count,将其初始化为 k,每遍历一个节点就将 count--。直到某次递归的时候,count 的值等于 1,说明此时的结点就是我们要找的结果。
算法流程:
定义一个全局的变量 count,在主函数中初始化为 k 的值(不用全局也可以,当成参数传入递归过程中);
递归函数的设计:int dfs(TreeNode* root):返回值为第 k 个结点;
递归函数流程(中序遍历):
递归出口:空节点直接返回 -1,说明没有找到;
去左子树上查找结果,记为 retleft:
- a. 如果
retleft == -1,说明没找到,继续执行下面逻辑; - b. 如果
retleft != -1,说明找到了,直接返回结果,无需执行下面代码(剪枝);
如果左子树没找到,判断当前结点是否符合:
- a. 如果符合,直接返回结果;
如果当前结点不符合,去右子树上寻找结果。
class Solution {
public:int cnt, ret;int kthSmallest(TreeNode* root, int k) {cnt = k;dfs(root);return ret;}void dfs(TreeNode* root){if(root == nullptr || cnt == 0) return;dfs(root->left);if(--cnt == 0){ret = root->val;return;}dfs(root->right);}
};
257. 二叉树的所有路径 - 力扣(LeetCode)
解法(DFS 回溯):
算法思路:
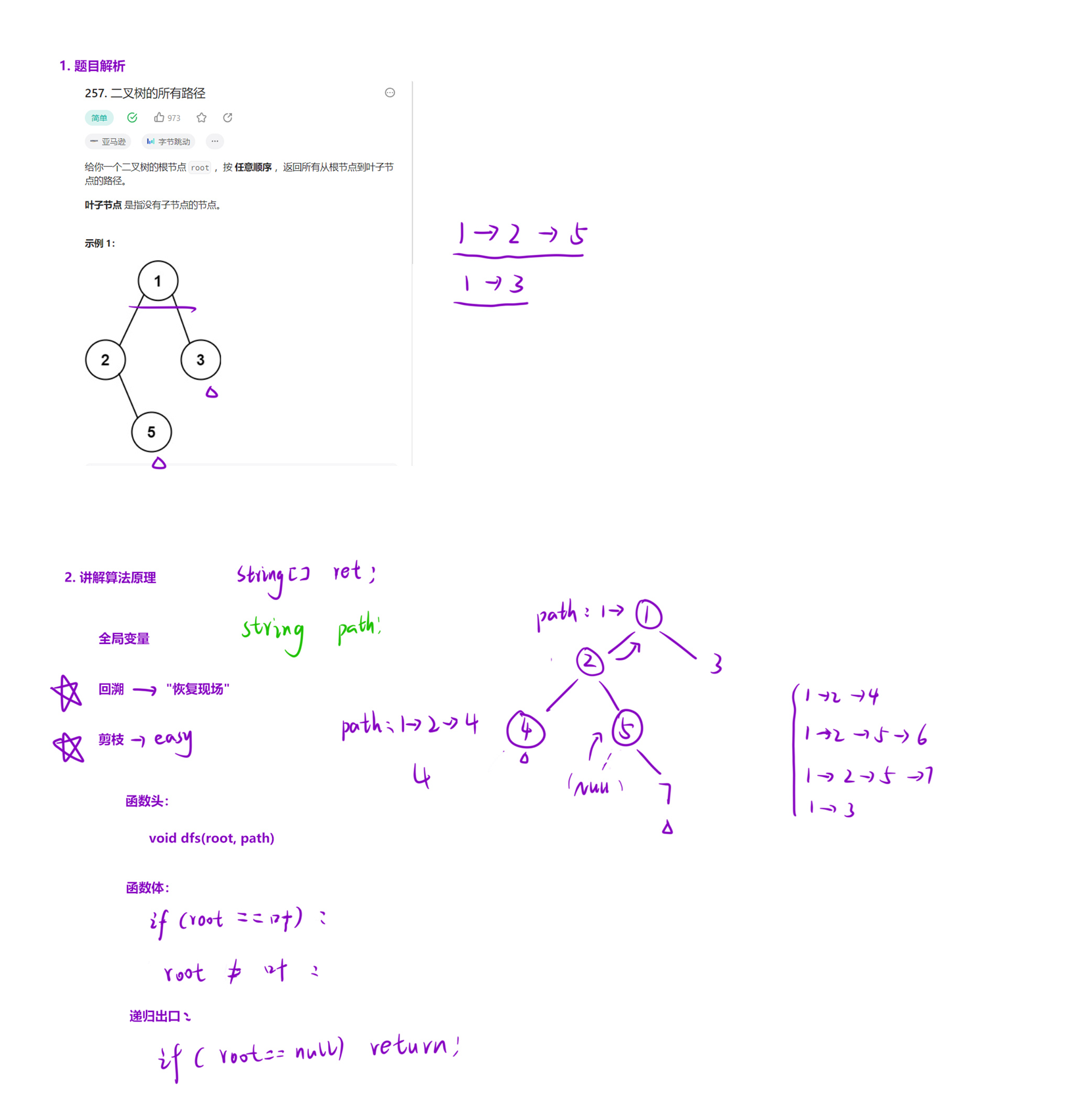
要找到从根节点到叶子节点的所有路径,核心是利用深度优先遍历(DFS) 遍历树的每一条分支,同时通过回溯记录并维护当前路径,避免重复存储中间状态。
-
路径记录:用一个临时列表存储当前遍历的路径(从根到当前节点的节点值);
-
终止条件:当遍历到叶子节点(左右子节点均为空)时,将当前路径拼接成 “节点值 -> 节点值” 的字符串,加入结果列表;
-
回溯逻辑:遍历完当前节点的左子树或右子树后,需要从临时列表中删除当前节点值,回到上一层节点,继续探索其他分支(避免下一条路径包含当前节点)。
算法流程:
递归函数设计:void dfs(TreeNode* root, vector<int>& path, vector<string>& result)
参数:
-
root:当前遍历的节点; -
path:临时存储当前路径的列表; -
result:存储所有有效路径的字符串列表;
函数作用:遍历以 root 为根的子树,记录所有从 root 到叶子节点的路径。
递归流程:
若当前节点为空,直接返回(递归出口);
将当前节点值加入临时路径 path;
判断是否为叶子节点:
-
若是:将
path中的值拼接成 “a->b->c” 格式的字符串,存入result; -
若不是:递归遍历左子树和右子树;
回溯:从 path 中删除当前节点值,回到上一层节点。
class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {dfs(root, "");return ret;}void dfs(TreeNode* root, string path){if(root == nullptr) return;path += to_string(root->val);if(root->left == nullptr && root->right == nullptr){ret.push_back(path);return;}path += "->";dfs(root->left, path);dfs(root->right, path);}
};
注意:
将代码改为使用引用传递void dfs(TreeNode* root, string& path)时,会导致所有递归调用共享同一个path变量。这会带来问题,因为:
- 在递归深入时,
path会不断累积节点值 - 当回溯时,
path不会自动恢复到上一层的状态
例如,当你从左子树回溯到父节点再访问右子树时,左子树添加的节点值仍然保留在path中,导致生成的路径包含错误的节点序列。
原代码使用值传递string path的好处是:
- 每次递归调用都会创建
path的副本 - 递归返回时自动恢复到上一层的状态
- 不需要手动进行字符串的拼接与还原操作
如果一定要使用引用传递,需要在递归前后手动管理path的状态(添加后再删除),这样会使代码更复杂且容易出错:
void dfs(TreeNode* root, string& path) {if(root == nullptr) return;// 记录当前长度,用于回溯int len = path.length();if(len > 0) path += "->";path += to_string(root->val);if(root->left == nullptr && root->right == nullptr) {ret.push_back(path);} else {dfs(root->left, path);dfs(root->right, path);}// 回溯:删除当前节点添加的内容path.erase(len);
}
因此,对于这种二叉树路径记录的场景,使用值传递更为简洁和安全。
