学习笔记2: 深度学习之logistic回归梯度下降
梯度下降与参数更新优化
在得到代价函数后,关键是如何更新参数(如 www, bbb),以使模型表现最佳,即使得代价函数 J(w,b)J(w, b)J(w,b) 最小。
1. 梯度下降(Gradient Descent)
问题:如何找到合适的 w,bw, bw,b 使 J(w,b)J(w, b)J(w,b) 最小?
当只考虑 www(忽略 bbb),JJJ 是一元函数:
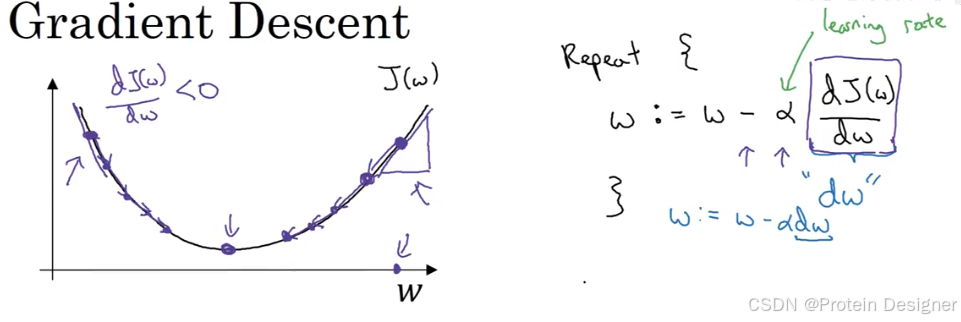
其中:
- α\alphaα:学习率 (learning rate)
- dwdwdw:www 的梯度
当初始点在极小值右侧,导数为正,www 会向左更新;左侧同理。不断迭代,最终收敛到极小值。
考虑两个参数 w,bw, bw,b 时,
w:=w−α∂J(w,b)∂w
w := w - \alpha \frac{\partial J(w, b)}{\partial w}
w:=w−α∂w∂J(w,b)
b:=b−α∂J(w,b)∂b
b := b - \alpha \frac{\partial J(w, b)}{\partial b}
b:=b−α∂b∂J(w,b)
不断计算偏导并更新参数,使 JJJ 达到最小。
2. logistic回归中的梯度下降
z^=σ(wTX+b)\hat z = \sigma(w^T X + b)z^=σ(wTX+b)
y^=a=σ(z)\hat y = a = \sigma(z)y^=a=σ(z)
交叉熵损失函数:
L(a,y)=−[yloga+(1−y)log(1−a)]
L(a, y) = -[y\log a + (1-y)\log(1-a)]
L(a,y)=−[yloga+(1−y)log(1−a)]
当样本 XXX 有两个特征 x1,x2x_1, x_2x1,x2 时,求导过程如下:
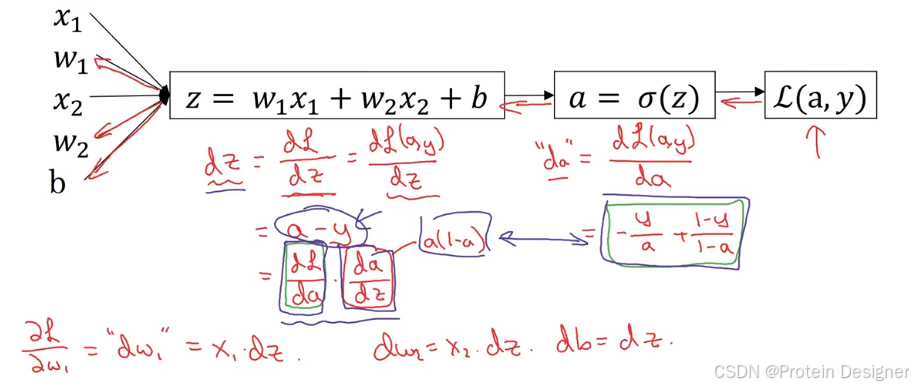
交叉熵损失函数对 aaa 的导数:
dLda=−ya+1−y1−a\frac{dL}{da} = -\frac{y}{a} + \frac{1-y}{1-a}dadL=−ay+1−a1−y
以下为AI求导过程,仅供参考。
Sigmoid函数对 zzz 的导数:
dadz=a(1−a)\frac{da}{dz} = a(1-a)dzda=a(1−a)
以下为AI求导过程,仅供参考。
损失函数对 zzz 的导数:
dLdz=a−y\frac{dL}{dz} = a - ydzdL=a−y
因此,三个参数的梯度分别为:
dw1=x1(a−y)dw_1 = x_1(a-y)dw1=x1(a−y)
dw2=x2(a−y)dw_2 = x_2(a-y)dw2=x2(a−y)
db=a−ydb = a-ydb=a−y
参数更新:
w1:=w1−αdw1w_1 := w_1 - \alpha dw_1w1:=w1−αdw1
w2:=w2−αdw2w_2 := w_2 - \alpha dw_2w2:=w2−αdw2
b:=b−αdbb := b - \alpha dbb:=b−αdb
3. 在 mmm 个样本上进行梯度下降
代价函数:
J(w,b)=1m∑i=1mL(y^(i),y(i))=−1m∑i=1m[y(i)logy^(i)+(1−y(i))log(1−y^(i))] J(w,b) = \frac{1}{m} \sum_{i=1}^m L(\hat y^{(i)}, y^{(i)}) = -\frac{1}{m} \sum_{i=1}^m [y^{(i)}\log \hat y^{(i)} + (1-y^{(i)})\log(1-\hat y^{(i)})] J(w,b)=m1i=1∑mL(y^(i),y(i))=−m1i=1∑m[y(i)logy^(i)+(1−y(i))log(1−y^(i))]
求导:
∂J(w,b)∂w1=1m∑i=1m∂L(a(i),y(i))∂w1=1m∑i=1mdw1(i)
\frac{\partial J(w,b)}{\partial w_1} = \frac{1}{m}\sum^m_{i=1}\frac{\partial L(a^{(i)},y^{(i)})}{\partial w_1}=\frac{1}{m}\sum^m_{i=1} dw_1^{(i)}
∂w1∂J(w,b)=m1i=1∑m∂w1∂L(a(i),y(i))=m1i=1∑mdw1(i)
伪代码:
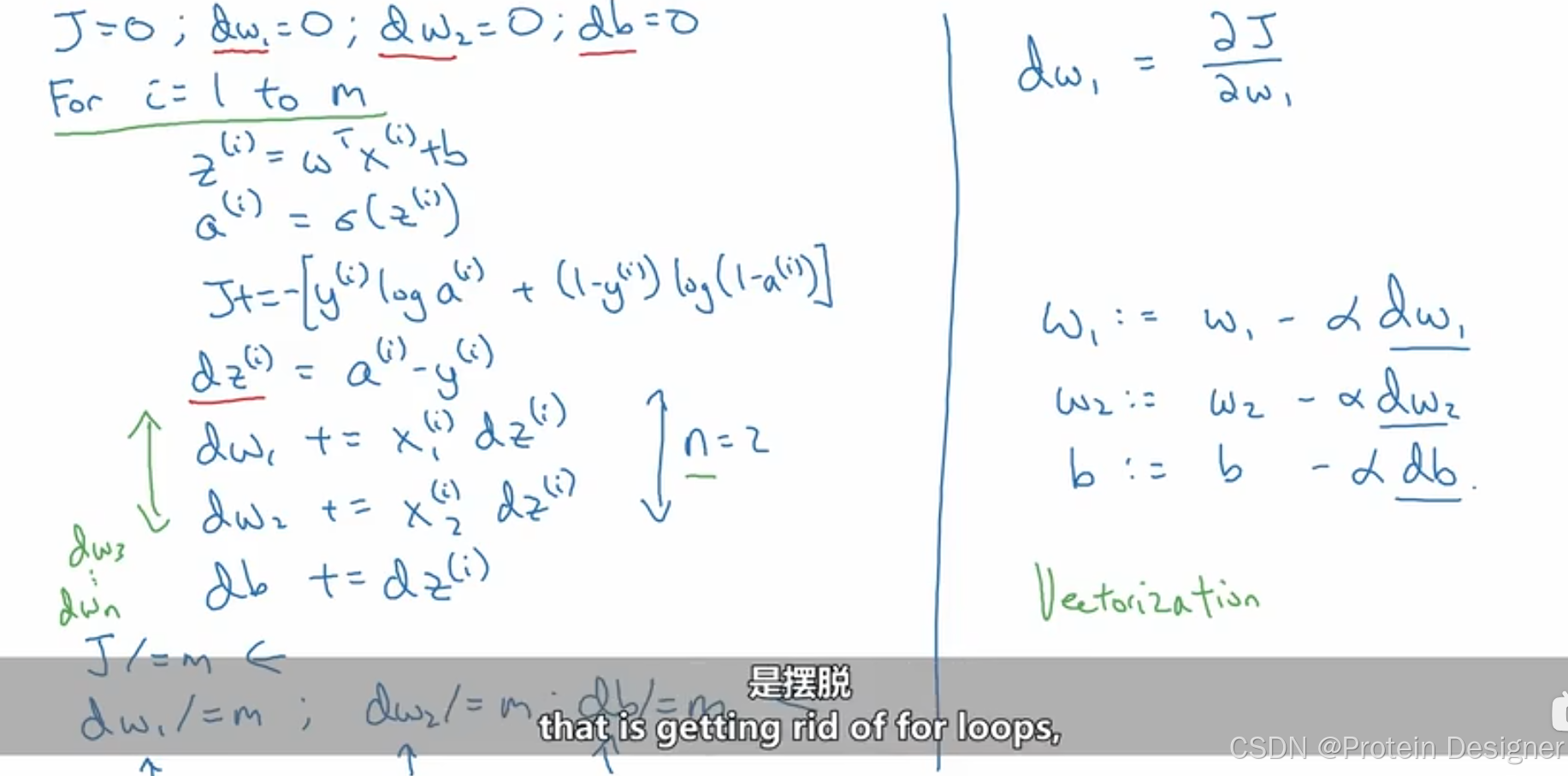
左侧:计算代价函数和所有参数的偏导
右侧:更新参数
但这样做可能会存在一个问题,我们当前的例子中只存在三个参数w1,w2,bw_1,w_2,bw1,w2,b,但在实际应用中可能存在nnn个www参数,这样将导致我们的计算中存在两个forforfor循环,计算mmm个样本,计算nnn个www参数,当计算量很大时,这样做就非常消耗资源了,因此引出向量化(vectorization)的概念。


