Java数据结构 - 优先级队列的模拟实现与使用

1.优先级队列的介绍

优先级队列(PriorityQueue)是一种优先级别先出队列的数据结构，底层使用堆来实现，而堆的底层是在完全二叉树的基础上扩展的，通常分为大根堆和小根堆，大根堆的根节点的值在树中最大的，而小根堆的根节点值是最小的，因此优先级队列会提供两个基本的操作，增加元素和出元素，实现优先级别高的元素位于顶部元素。

2. 堆

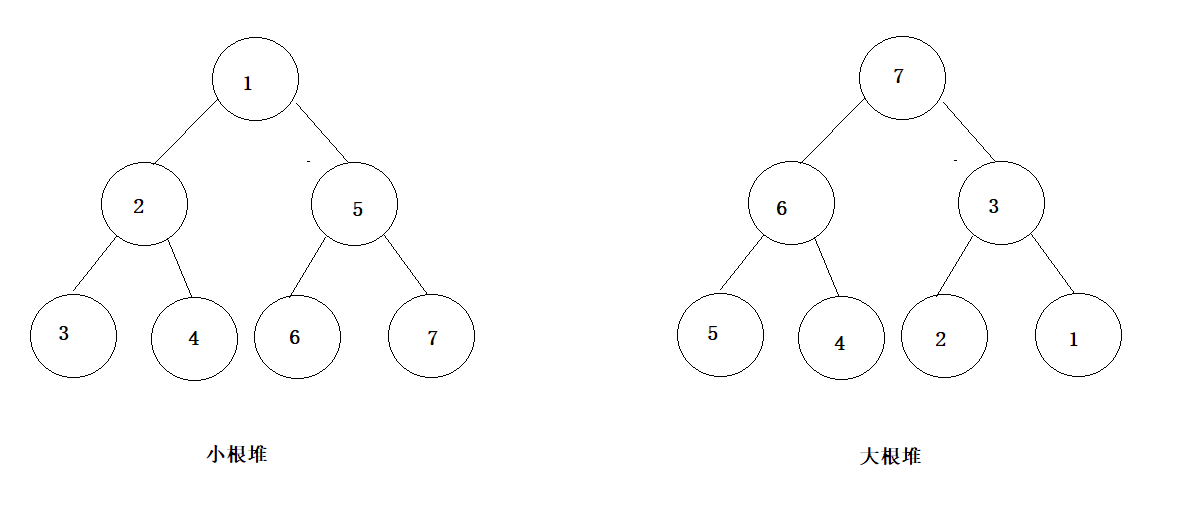
堆在底层是一棵完全二叉树，如果有一个集合为K = {k0,k1,k2 — kn} 按照完全二叉树的方式创建，每一个节点按照 0 到 n 编号，满足 Ki < K2i + 1 和 Ki < K2i + 2(父节点小于左孩子节点和右孩子节点)，称为小根堆，如果满足 Ki > K2i + 1 和 Ki > K2i + 2（父节点大于左孩子节点和右孩子节点）,称为大根堆。

2.1 向下调整

因为堆的结构具有一定的规律，在创建的时候会不断的进行比较调整，因此需要先定义一个函数来规定调整的方式，此处创建的是小根堆，以小根堆的调整方式创建函数。

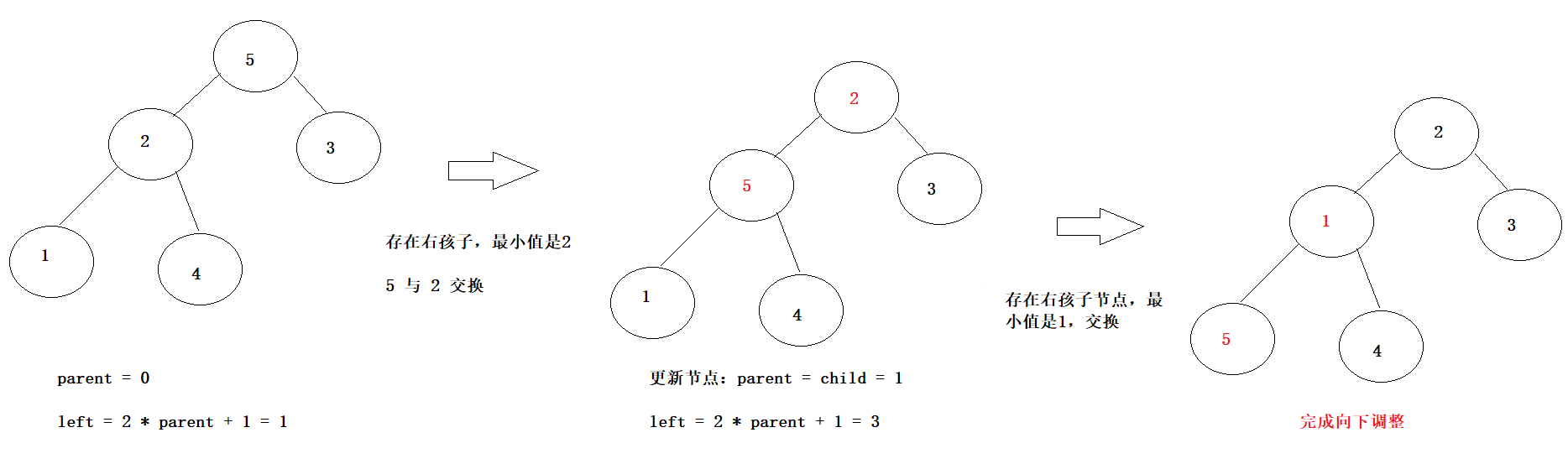
假设现在已经存在一棵二叉树【5，2，3，1，4】，该树不满足小根堆的定义，可以将每一个元素都按照小根堆的方式进行调整，如元素 5 是堆中最大的元素，按照小根堆的方式存储应该向下调整，因此可以定义一个函数siftDown,参数是需要调整的堆，以及调整元素的位置。

具体的思路：1.定义调整元素位置的孩子节点位置；2.判断是否存在右孩子节点，如果存在与左孩子节点比较获取最小值，如果最小值小于父亲节点的值，将孩子节点与父亲节点交换；3.重新更新节点位置，父亲节点赋值孩子节点，重复以上此循环直到结束；

 //向下调整public static void siftDown(int[] arr,int parent){int child = 2 * parent + 1;int size = arr.length;while(child < size){//是否存在右孩子，存在找最小值if(child + 1 < size && arr[child] > arr[child + 1]){child = child + 1;//右孩子小}//交换int t = arr[parent];arr[parent] = arr[child];arr[child] = t;//更新parentparent = child;child =  2 * parent + 1;}}

2.2 堆的创建

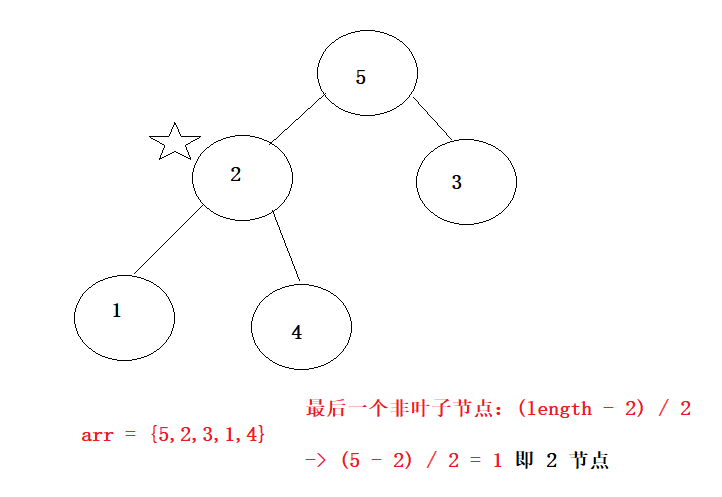
当具有调整方式时，将每一节点位置都进行调整，就可以获得小根堆，因为需要遍历每一个节点，可以使用一层循环，调整的位置是从最后一个非叶子节点开始，即从下往上遍历节点，该节点的位置是：(length - 2) / 2;

   public  void creatHeap(int[] arr){int root = (arr.length - 2) / 2;for (; root >= 0 ; root--) {siftDown(arr,root);}}

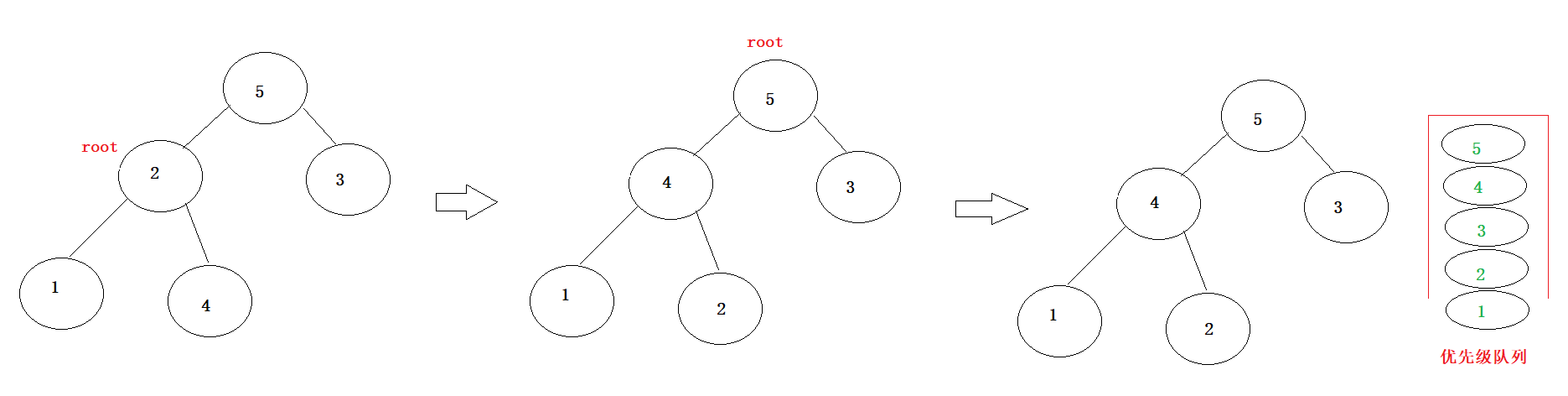
创建好的元素在优先级队列中的元素从上到下是有序的。

2.3 创建堆的时间复杂度

假设创建堆的完全二叉树的深度为 h，在倒数第二层开始向下调整，由于时间复杂度考虑的是最坏的情况，所以可以认为倒数第二层的节点都需要向下调整，调整的高度是从倒数第二层到倒数第一层，倒数第二层的节点树是 2 ^ (h-2),调整的次数是 1 * 2 ^ (h -2),依次类推，第一层只有根节点，最坏情况是向下调整到最下一层，高度为 h - 1,节点个数是1 ，调整次数是 1 * （h - 1),将倒数第二层到第一层所有调整次数相加计算就可以得到时间复杂度。

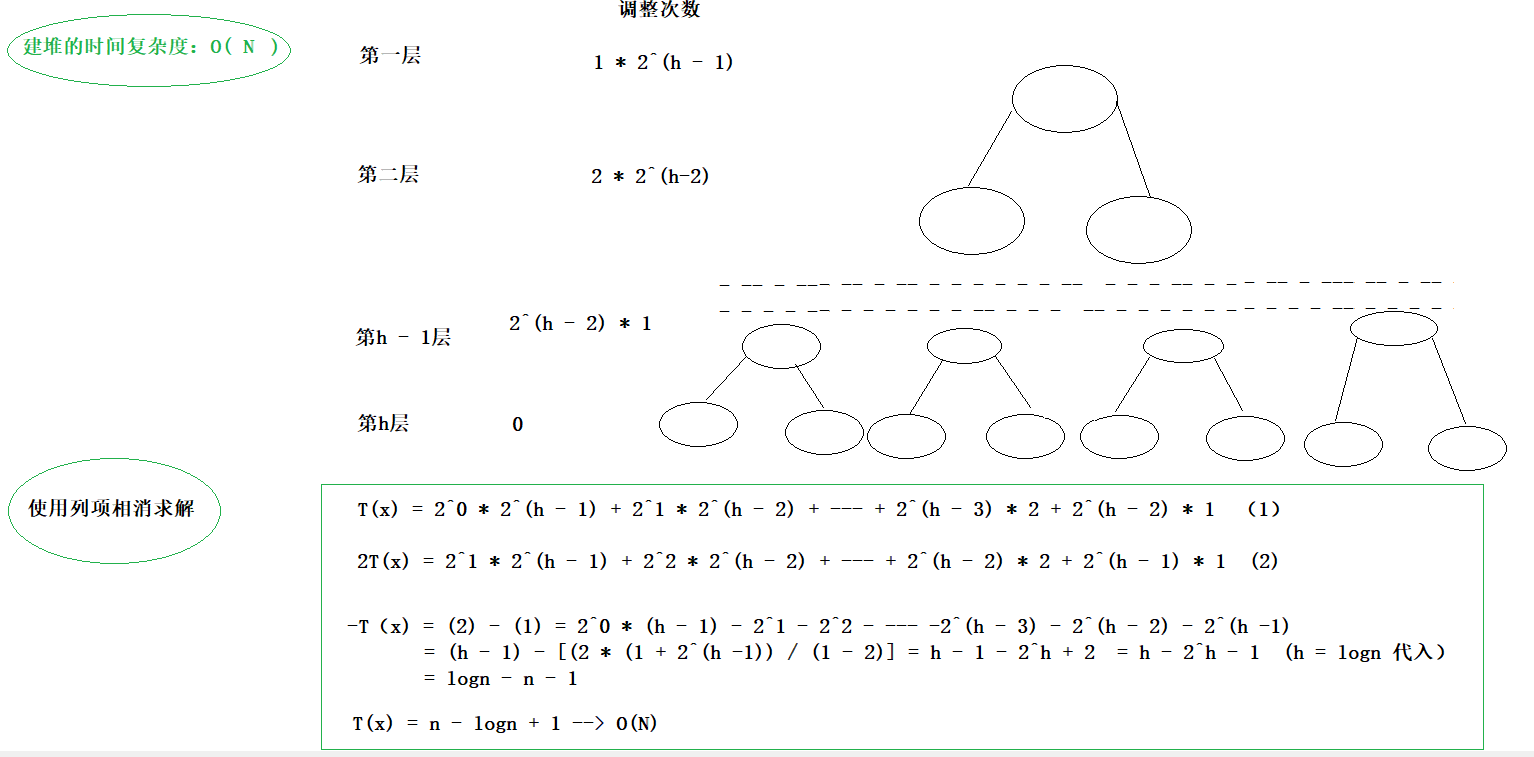
2.4 堆的插入

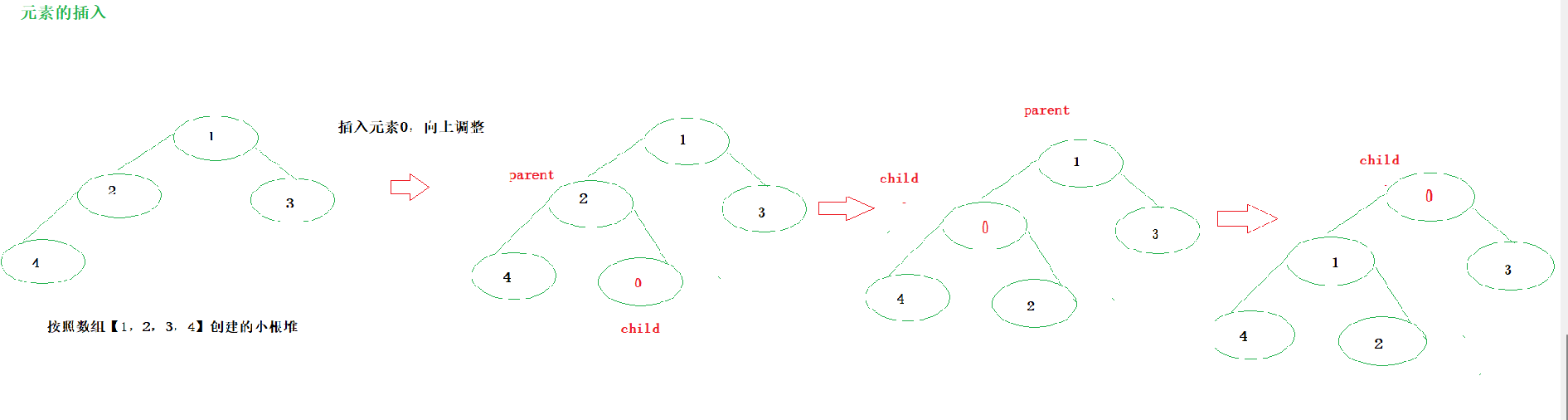
堆的创建是使用一个数组按照向下调整的方式创建好一个大根堆或者小根堆，在插入元素时，也需要使用到数组，先将元素加入到数组的末尾，即堆的末尾，但是需要考虑到数组的大小有限，需要考虑扩容问题；在元素插入后需要将元素进行向上调整，因此需要定义一个向上调整的函数siftUp完成元素的调整。

    public void siftUp(int[] arr,int child){int parent = (child - 1) / 2;//终止条件：parent >= 0 父节点下标不能越界 或者 child > 0 孩子节点为根节点，无需调整while(child > 0){//判断是否需要交换if(arr[child] < arr[parent]){//交换int tem = arr[child];arr[child] = arr[parent];arr[parent] = tem;//向上调整child = parent;parent = (child - 1) / 2;}else break;//满足小根堆的定义}}

按照数组【1，2，3，4】创建的小根堆后插入0元素，就可以使用向上调整，将0元素调整到根节点的位置。

2.5 堆的删除

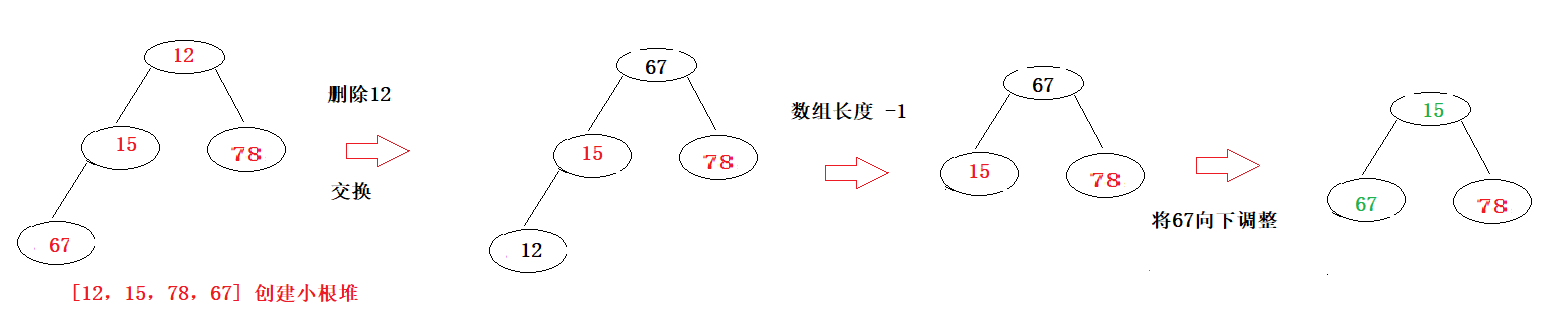
堆的删除不是真正将元素删去，而是将根节点的的元素与末尾元素交换，交换后将根节点元素向下调整，并将数组的实际长度 - 1，完成删除操作。

    int length;//数组长度public void delete(int[] arr){int top = 0,bottom = arr.length - 1;//1.交换int tem = arr[top];arr[top] = arr[bottom];arr[bottom] = tem;//2.数组大小-1length--;//3.向下调整siftDown(arr,0);}

按照数组【12，15，78，67】创建的小根堆，将12元素从堆中删除。

3. 堆模拟实现优先级队列

定义一个数组，数组实际元素个数和默认容量，定义三个构造函数，一个初始化默认容量为8，一个自定义容量，一个使用集合类创建；实现增加元素offer方法，删除元素方法poll方法，查看队列顶部元素peek方法，和获取队列大小size方法。

3.1 构造方法的实现

成员变量包括Object类型的数组，数组中实际的元素个数，和一个默认初始容量为8；
第一个构造函数将数组的容量初始化为8，第二个构造函数带一个参数指定初始化容量，第三个构造方法带一个容器类型的参数Collection,按照容器元素初始化数组。

import java.util.Arrays;
//实现泛型的队列，因为需要泛型元素比较，所以得使用Comparable接口
public class MyPriorityQueue<E extends Comparable<E>> {//成员变量的定义private Object[] arrays;private int size;private int DEFAULT_INITIALIZATION_CAPACITY = 8;//默认容量//构造函数//1.默认容量public MyPriorityQueue(){arrays = new Object[DEFAULT_INITIALIZATION_CAPACITY];}//2.容量不能小于1public MyPriorityQueue(int capacity){if(capacity < 1) throw new IllegalArgumentException();arrays = new Object[capacity];}//3.使用集合类接口创建public MyPriorityQueue(Collection<? extends E> collection){int length = collection.size();arrays = new Object[length];//1.迭代器Iterator<? extends E> iterable = collection.iterator();while(iterable.hasNext()){arrays[size++] = iterable.next();}//2.直接forEach
//      for(E e : collection){
//            arrays[size++] = e;
//      }//向下调整for (int root = (size -2) / 2; root >= 0 ; root--) {siftDown(root);}}
}

3.2 offer方法

offer方法的实现：

1.如果加入的参数为空，不能加入队列，返回false；

2.在数组的末尾添加指定的元素，需要考虑扩容的问题，当容量不足，元素个数小于64时2倍扩容，大于64时1.5倍扩容。

3.在末尾添加元素后，元素可能不满足小根堆的定义，将该元素向上调整，调用siftUp方法，调整完成，size++，返回true。

 public void siftUp(int child){int parent = (child - 1) / 2;//终止条件：parent >= 0 父节点下标不能越界 或者 child > 0 孩子节点为根节点，无需调整while(child > 0){//判断是否需要交换E o1 = (E)arrays[child];E o2 = (E)arrays[parent];//E是泛型：String Integer Double Long Float Character Byte//都实现了Comparable接口，可以直接使用compareTo方法if(o1.compareTo(o2) < 0){Object tem = arrays[child];arrays[child] = arrays[parent];arrays[parent] = tem;child = parent;parent = (child - 1) / 2;}else break;//满足小根堆的定义}}public boolean offer(Object data){//对象为空if(data == null) return false;//扩容：小于64 ，2倍扩容 大于64 1.5倍扩容if(arrays.length == size){if(size < 64)arrays = Arrays.copyOf(arrays,size * 2);else{int capacity = (int)(size * 1.5);arrays = Arrays.copyOf(arrays,capacity);}}//加入元素arrays[size] = data;//向上调整siftUp(size++);//实际大小++return true;}

3.3 poll方法

poll方法的实现：

1.使用poll方法要确保队列中存在元素才可出队列，否则会抛空指针异常；

2.将队列的顶部元素和末尾元素交换，保存此时size下标的元素，**让size–,**交换后将顶部元素向下调整；

3.返回末尾元素;

//向下调整public  void siftDown(int parent){int child = 2 * parent + 1;int size = this.size;while(child < size){//是否存在右孩子，存在找最小值E o = (E)arrays[child];if(child + 1 < size && o.compareTo((E)arrays[child + 1]) > 0){child = child + 1;//右孩子小}E o1 = (E)arrays[parent];E o2 = (E)arrays[child];//父节点值 大于 孩子节点值就交换if(o1.compareTo(o2) > 0){//交换Object t = arrays[parent];arrays[parent] = arrays[child];arrays[child] = t;//更新parentparent = child;child =  2 * parent + 1;}else break;}}public E poll(){//出队列元素不能为空if(size == 0) throw new NullPointerException();int top = 0,bottom = size - 1;//队头和对位元素//1.交换Object tem = arrays[top];arrays[top] = arrays[bottom];arrays[bottom] = tem;//2.向下调整siftDown(0);E ret = (E)arrays[size-- - 1];//3.返回return ret;}

3.4 peek方法

peek方法使用需要注意队列中不能为空，如果为空需要抛异常，不为空返回队列顶部元素

    public E peek(){//没有元素，抛异常if(size() == 0) throw new NullPointerException();return (E)arrays[0];}

3.5 size方法

获取队列元素个数可以调用size方法，返回size

    public int size(){return size;}

3.6 isEmpty方法

判断队列是否为空时使用isEmpty方法，为空返回true，为假返回false。

    public Boolean isEmpty(){return size == 0;} 

3.7 clear方法

回收队列时使用clear方法，clear方法的实现是将数组回收，size = 0；

    public void clear(){arrays = null;size = 0;}

3.8 测试模拟实现的优先级队列

测试创建的队列：加入字符串[“c” “b” “a” ] ,获取队头元素，获取大小，将元素全部出队列，再执行查看队头元素。

    public static void main(String[] args) {//1.默认容量MyPriorityQueue<String> myPriorityQueue = new MyPriorityQueue<>();myPriorityQueue.offer("c");myPriorityQueue.offer("b");myPriorityQueue.offer("a");System.out.println("队列顶部元素 ：" + myPriorityQueue.peek());//aSystem.out.println("队列大小: " + myPriorityQueue.size());//0myPriorityQueue.poll();//aSystem.out.println("出队列的元素：" + myPriorityQueue.poll());//bSystem.out.println("出队列的元素：" + myPriorityQueue.poll());//cSystem.out.println(myPriorityQueue.poll());//没有元素，抛异常}

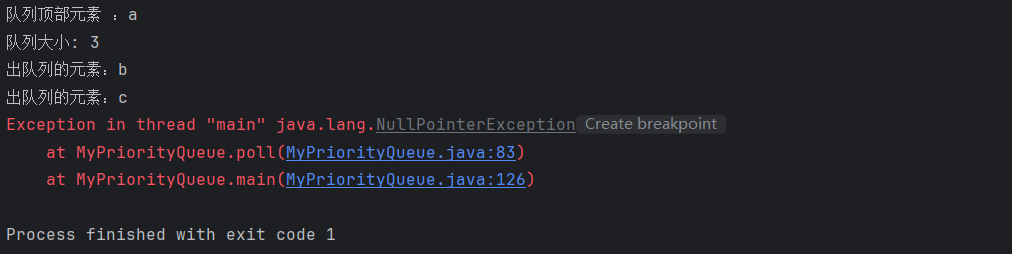
测试指定容量的优先级队列：容量默认为1，为Integer类型的数据，增加元素666，查看队列顶部元素，判断是否为空，回收队列，使用对象引用。

public static void main(String[] args) {//2.指定容量MyPriorityQueue<Integer> priorityQueue = new MyPriorityQueue<Integer>(1);//增加元素priorityQueue.offer(666);//获取队列顶部元素System.out.println(priorityQueue.peek());//判断是否为空System.out.println(priorityQueue.isEmpty());//回收队列priorityQueue.clear();//此时不能使用对象引用priorityQueue.offer(1);}

使用指定容器初始化优先级队列：创建一个ArrayList实例化的对象使用Collection类型接收，添加一些数据，创建优先级队列，参数为Collection类型的引用,查看队列顶部元素。

public static void main(String[] args) {Collection collection = new ArrayList();collection.add(162);collection.add(21);collection.add(145);MyPriorityQueue<Integer> priorityQueue = new MyPriorityQueue<>(collection);System.out.println(priorityQueue.peek());}

4.TopK问题

TopK问题是求解出现次数或者数值最大或者最小的前k个数，求解的方法可以使用排序后获取，或者也可以使用统计进行求解，这里主要是通过排序的方法解决TopK问题。

例如：给定一个数组【24，12，45，11，56，77，96】，获取数组中最大的三个数。

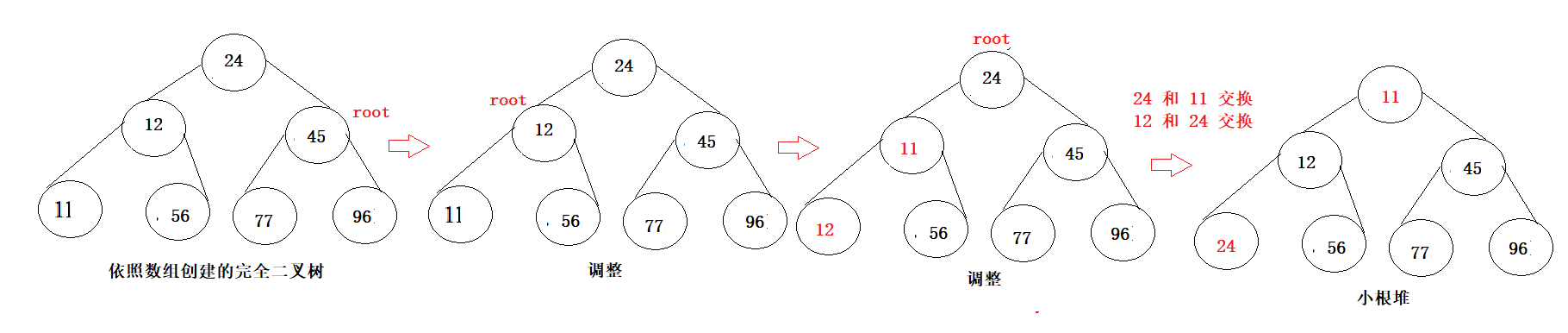
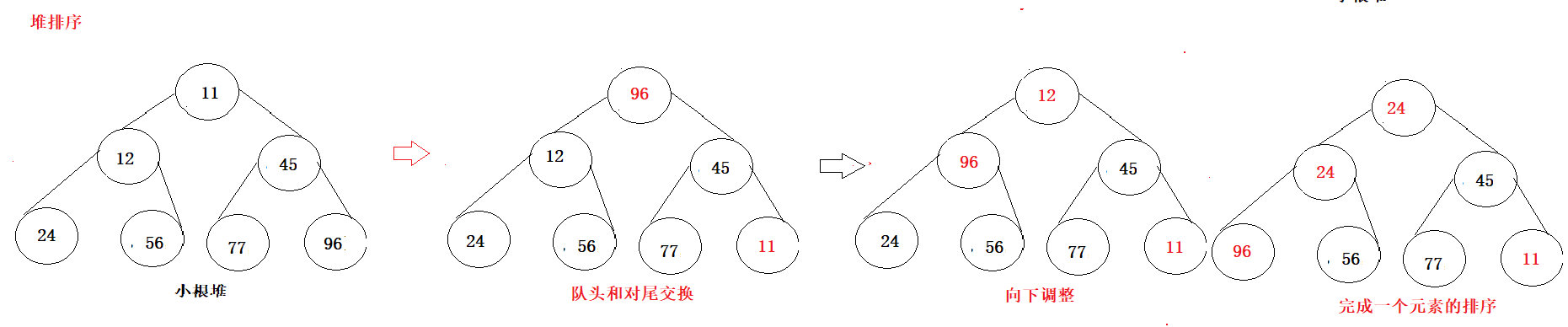
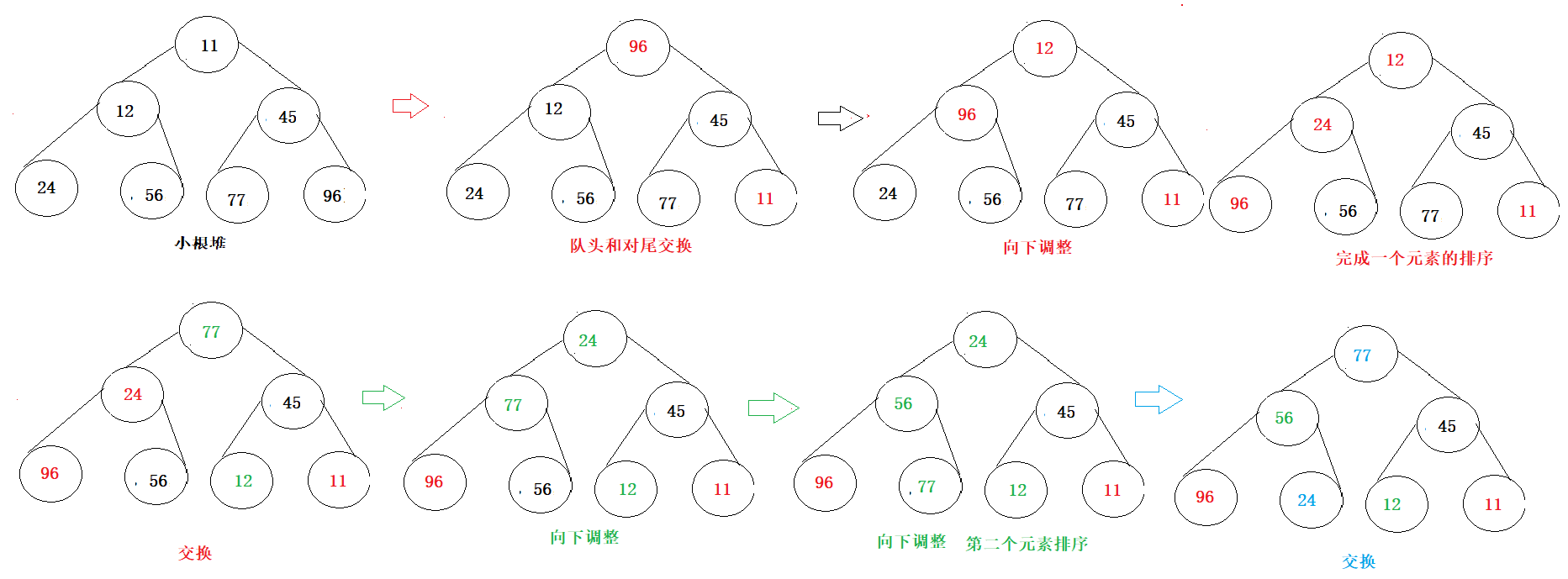
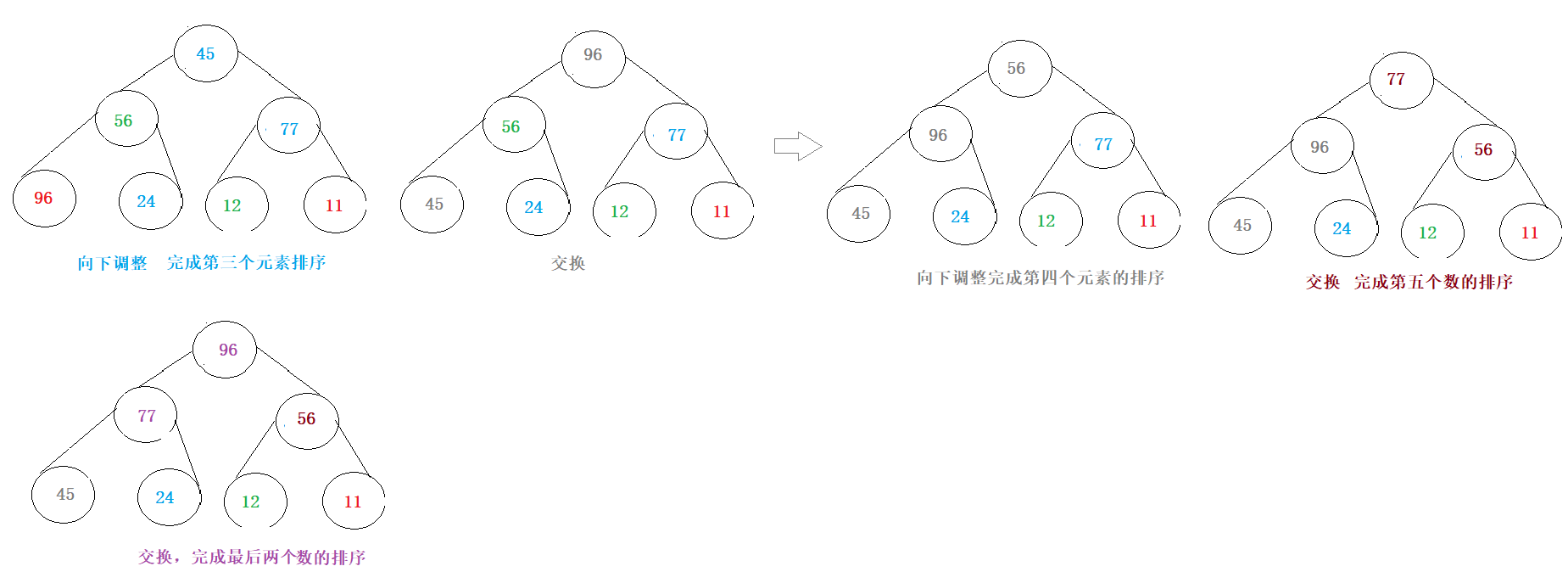
解决方法：1.创建一个小根堆；2.使用堆排序，排序后获取的前3个元素就是最大的。

因为是求最大的的前K个数，创建小根堆后，堆顶的元素就是最小的，将最小的元素和末尾的交换，此时末尾的元素就是最小的，再将堆顶元素向下调整，以此类推，从后往前元素有小到大，最后前K个元素就是堆中最大的前K个。

class Solution {//向下调整public  void siftDown(int[] arr,int parent,int length){int child = 2 * parent + 1;int size = length;while(child < size){//判断是否有右孩子，并判断是否更新if(child + 1 < size &&  arr[child] > arr[child + 1]){child = child + 1;//右孩子小}//交换if(arr[parent] > arr[child]){int t = arr[parent];arr[parent] = arr[child];arr[child] = t;//更新parentparent = child;child =  2 * parent + 1;}else break;}}public void createHeap(int[] arr){int root = (arr.length - 2) / 2;for (; root >= 0 ; root--) {siftDown(arr,root,arr.length);}}public void HeapSort(int[] arr){if(arr == null || arr.length == 1) return;int length = arr.length;//使用for循环遍历交换for (int i = length - 1; i > 0 ; i--) {//1.交换int tem = arr[0];arr[0] = arr[i];arr[i] = tem;//2.向下调整//交互后一些元素已经有序，不需要再被调整，所以需要--lengthsiftDown(arr,0,--length);}}public  int[] maxK(int[] arr, int k) {if(k == 0) return new int[0];//1.创建小堆createHeap(arr);//2.堆排序HeapSort(arr);//3.获取前k个数k = Math.min(k,arr.length);int[] ret = new int[k];int i = 0,j = 0;while(k-- != 0){ret[i++] = arr[j++];}return ret;}
}

测试查找最大的前3个数

public static void main(String[] args) {Solution solution = new Solution();int[] arr = {24,12,45,11,56,77,96};int[] tem = solution.maxK(arr,3);System.out.print("arr数组中最大的前" + 3 + "个数是:[");for(int p : tem){System.out.print(p + " ");}}

堆排序的时间复杂度

时间复杂度考虑的是最坏的情况，即每一个元素都需要被调整，堆中最后一层的元素个数为2^(h-1)
,最坏情况下交换后又被调整到最下面一层，调整的高度为logn，以此类推，倒数第二层的个数为2^(h - 2),调整的高度为logn - 1，直到第二层，元素个数为2^1,调整高度为1，将所有调整次数相加得到时间复杂度O(nlogn).