栈和队列的学习

一、栈(Stack)

1、概念

栈（Stack）是计算机科学中最基础且高频使用的线性数据结构之一，核心遵循 “后进先出”（Last-In-First-Out，LIFO）原则 —— 即最后加入栈的元素，会最先被取出，类似日常生活中 “叠盘子”（最后叠的盘子先拿）、“堆书”（最后放的书先取）的场景。掌握栈的知识，是理解后续复杂算法（如表达式求值、递归调用）和工程应用（如浏览器历史记录）的关键，以下从核心概念、实现方式、操作特性、特殊栈及典型应用展开，系统梳理学习要点。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据在栈顶。

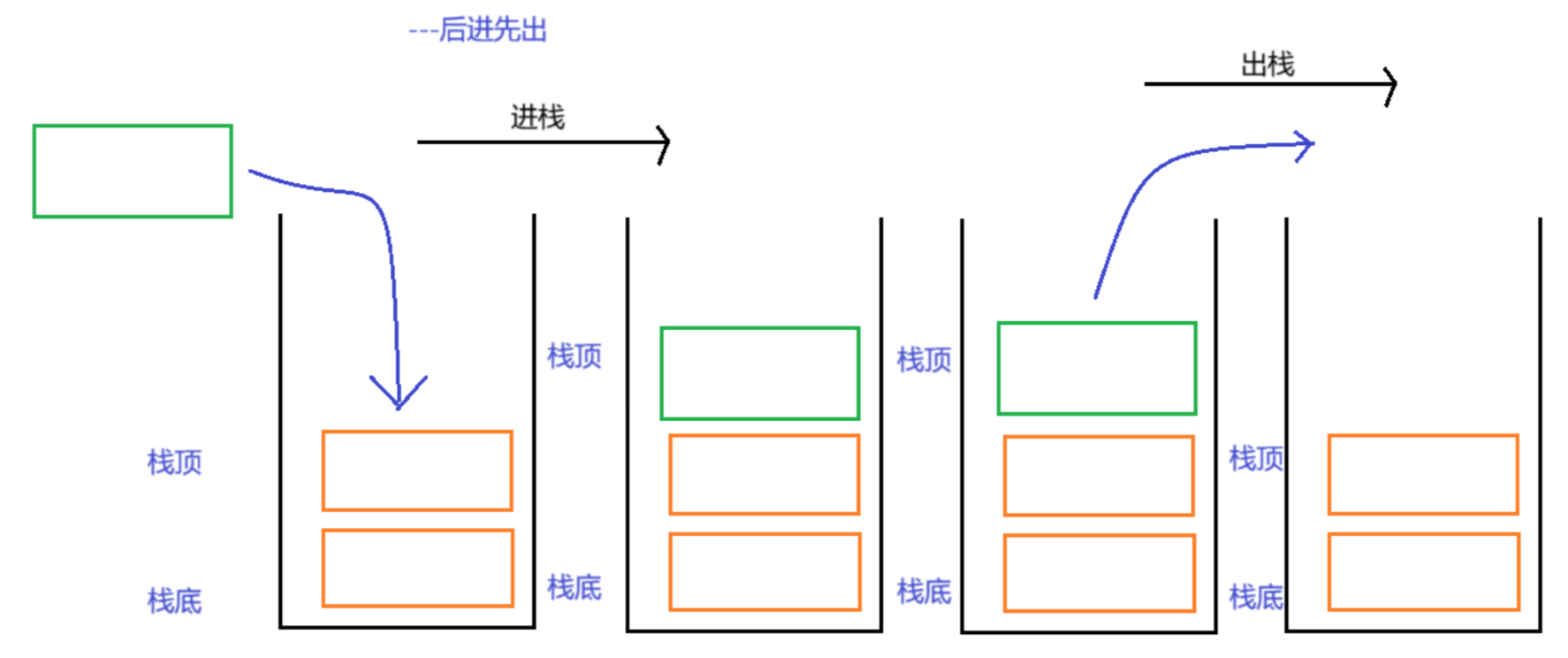
在现实生活中，也有这样的例子，如猎枪的子弹，羽毛球筒里的羽毛球，都和栈一样后进先出。

（同样的，不一定是进一个出一个，顺序可以是随机的，根据需求来）
这是一些定义

**2、栈的存储方式：

栈有两种基本存储方式:
顺序存储：利用一段连续的内存空间进行存储。
链式存储：利用非连续的内存空间存储，元素之间使用指针进行链接。（通常单链表实现，栈顶是表头，栈底的表尾）
两种实现方式对比

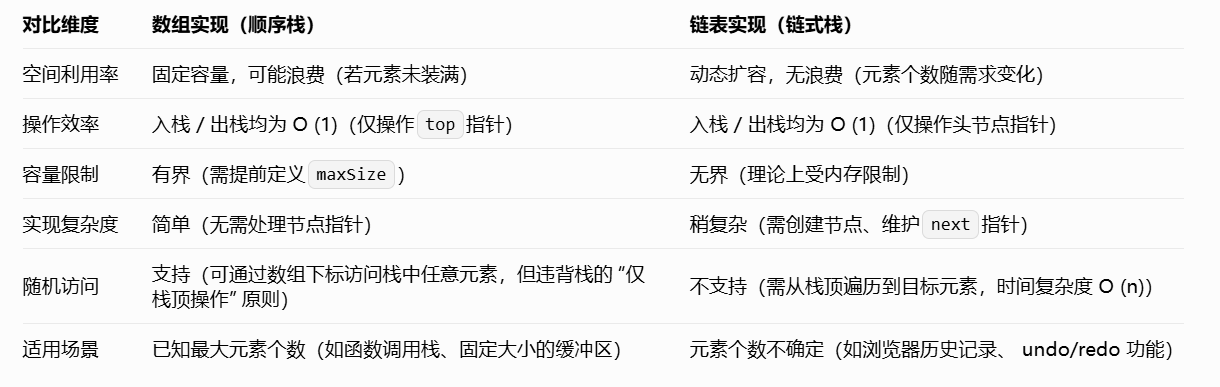
栈的基本操作及时间复杂度

栈的操作严格围绕 “栈顶” 展开，核心操作仅 3 类（入栈、出栈、查看栈顶），所有操作的时间复杂度均为O(1)（无需遍历元素，仅操作top指针或头节点）

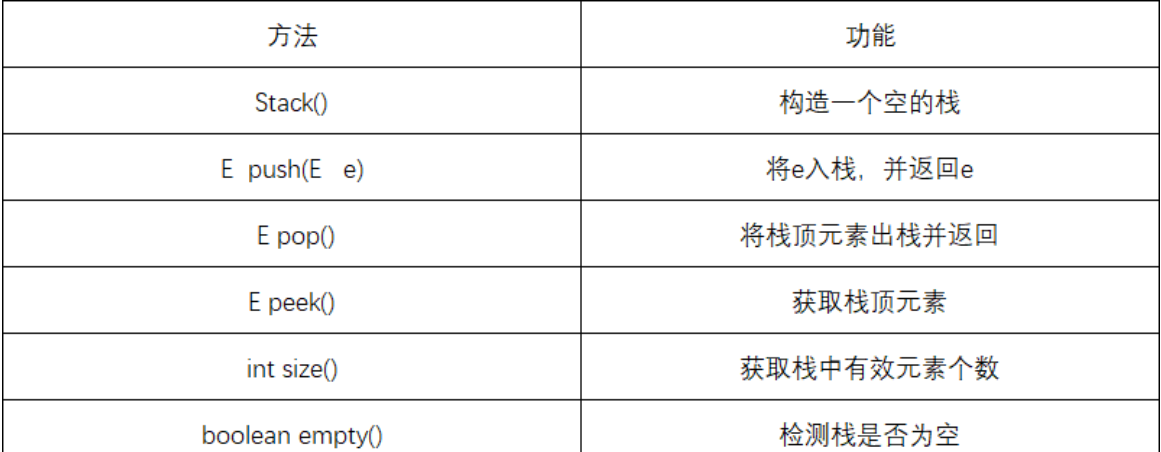
栈的两种核心实现方式

栈的本质是 “仅允许栈顶操作”，常见实现方式有数组（顺序存储） 和链表（链式存储） ，二者在空间利用率、操作效率上各有优劣，需根据场景选择：

1. 数组实现：顺序栈

用固定大小的数组存储栈元素，通过一个top指针（变量）记录栈顶位置，控制入栈、出栈操作。
实现细节（以 Java 为例）博主学的Java：

• 初始化：定义数组stack（存储元素）和top变量（初始值为-1，表示空栈），maxSize为栈的最大容量。

private int[] stack;
private int top = -1; // 栈顶指针，空栈时为-1
private int maxSize;public ArrayStack(int maxSize) {this.maxSize = maxSize;stack = new int[maxSize];
}

• 入栈（push）：若栈未满，top先加 1，再将元素存入top指向的数组位置。

public void push(int value) {if (isFull()) {throw new RuntimeException("栈满，无法入栈！");}top++;stack[top] = value;
}

• 出栈（pop）：若栈非空，先取出top指向的元素，再将top减 1。

public int pop() {if (isEmpty()) {throw new RuntimeException("栈空，无法出栈！");}int value = stack[top];top--;return value;
}

2. 链表实现：链式栈

用单链表存储栈元素，通常将链表的头节点作为栈顶（无需遍历链表即可操作栈顶，效率更高），top指针指向头节点，栈底为链表的尾节点（固定不变）。
实现细节（以 Java 为例）：
定义节点类：包含 “数据域”（存储元素）和 “下一个节点指针”（next）。

class Node {public int data;public Node next;public Node(int data) {this.data = data;}
}

初始化：top指针初始为null（表示空栈），无需提前定义容量（动态扩容）。

private Node top = null; // 栈顶指针，空栈时为null

入栈（push）：创建新节点，将新节点的next指向原栈顶（top），再更新top为新节点（新节点成为新栈顶）。

public void push(int value) {Node newNode = new Node(value);newNode.next = top; // 新节点指向原栈顶top = newNode; // 栈顶更新为新节点
}

出栈（pop）：若栈非空，先记录原栈顶节点的数据，再将top更新为原栈顶的next节点（原栈顶节点被回收），最后返回数据。

public int pop() {if (isEmpty()) {throw new RuntimeException("栈空，无法出栈！");}int value = top.data;top = top.next; // 栈顶指向原栈顶的下一个节点return value;
}

力扣的一些扩展栈功能

1. 最小栈（Min Stack）

题目：在 O (1) 时间内获取栈中的最小元素（基础栈获取最小值需遍历，时间复杂度 O (n)）。
实现思路：用 “双栈” 结构 ——

• 主栈（mainStack）：存储所有元素，正常执行push、pop操作；
• 辅助栈（minStack）：仅存储 “当前栈中的最小值”，与主栈同步操作：
• 入栈时：若辅助栈为空，或新元素≤辅助栈顶元素，则新元素入辅助栈；
• 出栈时：若主栈弹出的元素等于辅助栈顶元素，则辅助栈同步弹出（确保辅助栈顶始终是当前最小值）。

class MinStack {private Stack<Integer> mainStack;private Stack<Integer> minStack;public MinStack() {mainStack = new Stack<>();minStack = new Stack<>();}public void push(int val) {mainStack.push(val);// 辅助栈仅存最小值或更小值if (minStack.isEmpty() || val <= minStack.peek()) {minStack.push(val);}}public void pop() {int val = mainStack.pop();// 若弹出的是最小值，辅助栈同步弹出if (val == minStack.peek()) {minStack.pop();}}public int top() {return mainStack.peek();}public int getMin() {return minStack.peek(); }
}

应用场景：需要频繁获取最小值的场景（如股票价格波动、数据监控）。

2. 双端栈（Double-Ended Stack）

需求：在一个数组中实现两个栈，共享数组空间，分别从数组的两端向中间生长（左栈从 0 开始，右栈从maxSize-1开始），提高空间利用率。核心逻辑：
左栈栈顶指针leftTop（初始-1），右栈栈顶指针rightTop（初始maxSize）；
入栈时：左栈leftTop+1后存元素，右栈rightTop-1后存元素；
栈满条件：leftTop + 1 == rightTop（两个栈的栈顶相邻，数组无剩余空间）。
应用场景：元素个数不确定，但总个数不超过数组容量的场景（如内存受限的嵌入式系统）。

3. 单调栈（Monotonic Stack）
   需求：栈内元素始终保持 “单调递增” 或 “单调递减” 的顺序，用于高效解决 “Next Greater Element”（下一个更大元素）类问题。核心特性：
   单调递增栈：栈内元素从栈底到栈顶依次增大（新元素入栈前，弹出所有比它大的元素，确保单调性）；
   单调递减栈：栈内元素从栈底到栈顶依次减小（新元素入栈前，弹出所有比它小的元素）。

public int[] nextGreaterElement(int[] nums) {int[] res = new int[nums.length];Stack<Integer> stack = new Stack<>(); // 单调递减栈（存索引）for (int i = nums.length - 1; i >= 0; i--) {// 弹出比当前元素小的元素（它们不可能是当前元素的“下一个更大元素”）while (!stack.isEmpty() && nums[stack.peek()] <= nums[i]) {stack.pop();}// 栈空则无更大元素，否则栈顶索引对应的值就是res[i] = stack.isEmpty() ? -1 : nums[stack.peek()];stack.push(i); // 当前元素索引入栈，供左侧元素判断}return res;
}

栈的典型应用场景

1.编程语言的 “函数调用栈”
这是栈最核心的底层应用 —— 编程语言（如 Java、C++）通过 “调用栈” 管理函数的调用和返回：

• 函数调用时：将函数的 “返回地址”“局部变量”“参数” 压入栈中（入栈）；
• 函数执行完毕时：从栈顶弹出该函数的信息，回到调用它的位置（出栈）；
• 递归调用的本质：就是反复将递归函数的信息压入栈，直到触发 “递归终止条件” 后，再依次出栈执行返回逻辑（若递归深度过大，会导致
  “栈溢出”——Stack Overflow）。

2.表达式求值（中缀转后缀 / 前缀）

数学表达式（如3 + 4 * 2 - (1 + 5)）的计算，需处理 “运算符优先级” 和 “括号优先级”，栈是实现该逻辑的核心工具：

• 中缀表达式转后缀表达式（逆波兰表达式）：用栈存储运算符，根据优先级决定运算符是否出栈；
• 后缀表达式求值：用栈存储操作数，遇到运算符时弹出两个操作数计算，结果再入栈。
  3.浏览器 / 编辑器的 “历史记录”
  浏览器前进 / 后退：用两个栈（backStack存储后退历史，forwardStack存储前进历史）：
• 访问新页面：backStack压入当前页面，清空forwardStack；
• 点击后退：backStack弹出当前页面，压入forwardStack，显示backStack栈顶页面；
• 点击前进：forwardStack弹出页面，压入backStack，显示该页面。
• 编辑器 Undo/Redo（撤销 / 重做）：逻辑与浏览器历史类似，用栈存储操作记录，Undo 弹出最近操作，Redo 恢复弹出的操作。

二、队列(Queue)

1、概念
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾（Tail/Rear） 出队列：进行删除操作的一端称为队头 （Head/Front）

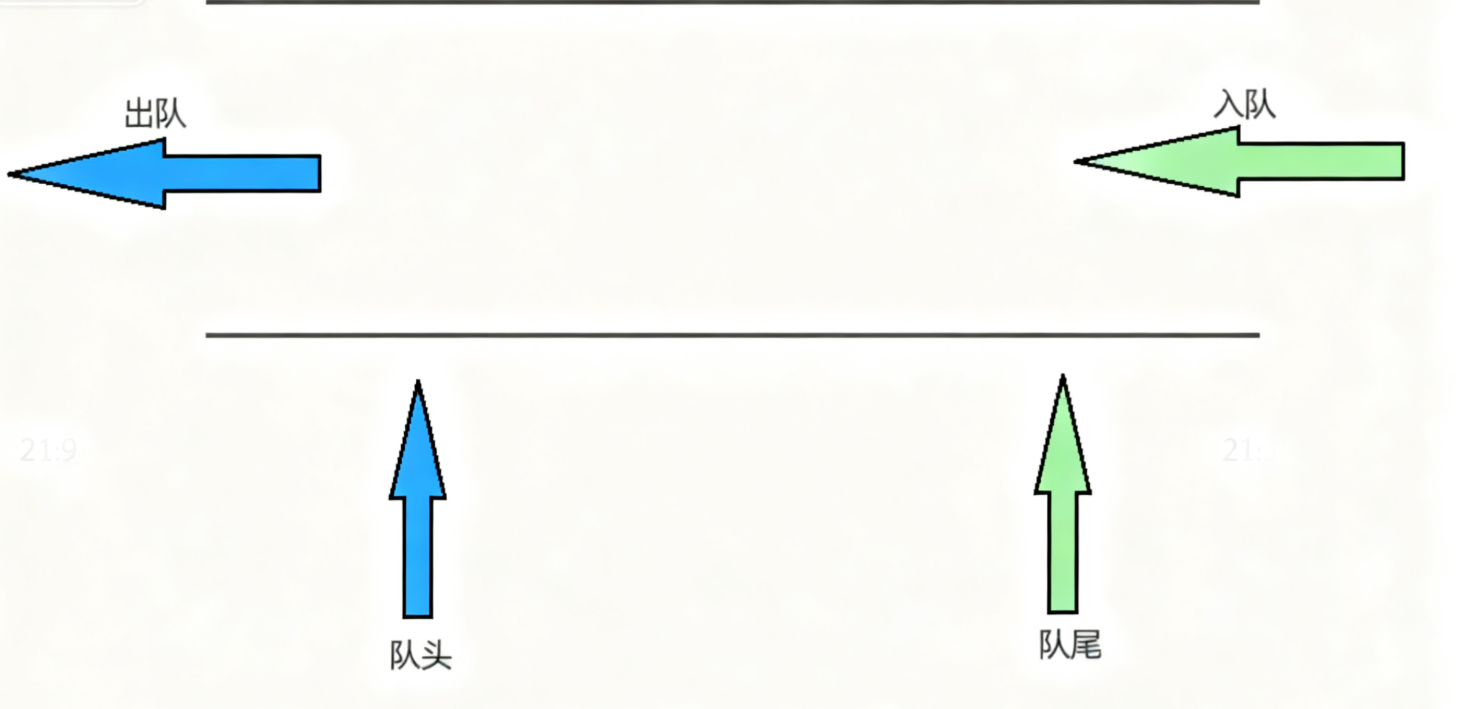
队列的专业术语

1. 数组实现：顺序队列
用固定大小的数组存储队列元素，通过两个指针（front记录队头，rear记录队尾）控制操作。
实现细节：

• 初始状态：front = rear = 0（队空）
• 入队（Enqueue）：若队列未满，将元素存入rear指向的位置，rear += 1。
• 出队（Dequeue）：若队列非空，取出front指向的元素，front += 1。
  2. 链表实现：链式队列
  用单链表存储队列元素，通常定义两个指针：front指向链表头（队头），rear指向链表尾（队尾），链表节点包含 “数据域” 和 “下一个节点指针”。
  实现细节：
• 初始状态：front = rear = null（或指向一个 “哨兵节点”，简化空队列判断）。
• 入队（Enqueue）：创建新节点，若队空则front和rear均指向新节点；否则rear.next指向新节点，rear更新为新节点。
• 出队（Dequeue）：若队空则报错；否则取出front节点的数据，front更新为front.next（若出队后队空，需将rear也设为null）。
  常见的特殊队列
  基础队列的功能有限，实际应用中常基于其扩展出特殊队列，以满足特定场景需求：
  1. 循环队列（解决数组假溢出）
  将数组的首尾逻辑上连接（如数组下标maxSize-1的下一个位置是0），形成 “环形” 结构，彻底解决数组实现的 “假溢出” 问题。
  核心设计：
  判空条件：front == rear（与基础数组队列一致）。
  判满条件：(rear + 1) % maxSize == front（故意留出一个空位置，避免与判空条件冲突）。
  元素个数计算：(rear - front + maxSize) % maxSize（处理rear < front的环形情况）。

public class CircularQueue {private int[] queue;private int front; // 队头指针private int rear; // 队尾指针private int maxSize; // 队列最大容量// 初始化循环队列public CircularQueue(int capacity) {maxSize = capacity;queue = new int[maxSize];front = 0;rear = 0;}// 判断队列是否为空public boolean isEmpty() {return front == rear;}// 判断队列是否已满public boolean isFull() {return (rear + 1) % maxSize == front;}// 入队操作public boolean enqueue(int item) {if (isFull()) {System.out.println("队列已满，无法入队");return false;}queue[rear] = item;rear = (rear + 1) % maxSize;return true;}// 出队操作public int dequeue() {if (isEmpty()) {throw new RuntimeException("队列为空，无法出队");}int item = queue[front];front = (front + 1) % maxSize;return item;}// 获取队列元素个数public int size() {return (rear - front + maxSize) % maxSize;}// 打印队列元素public void printQueue() {if (isEmpty()) {System.out.println("队列为空");return;}int i = front;while (i != rear) {System.out.print(queue[i] + " ");i = (i + 1) % maxSize;}System.out.println();}public static void main(String[] args) {CircularQueue circularQueue = new CircularQueue(5);circularQueue.enqueue(1);circularQueue.enqueue(2);circularQueue.enqueue(3);System.out.println("入队 1、2、3 后队列：");circularQueue.printQueue();circularQueue.dequeue();circularQueue.dequeue();System.out.println("出队两次后队列：");circularQueue.printQueue();circularQueue.enqueue(4);circularQueue.enqueue(5);System.out.println("入队 4、5 后队列：");circularQueue.printQueue();System.out.println("队列是否已满：" + circularQueue.isFull());}
}

2. 双端队列（Deque）
允许在队头和队尾同时进行插入和删除的队列，是基础队列的扩展，兼具队列（FIFO）和栈（LIFO）的特性。
核心操作：
队头插入（addFirst）、队头删除（removeFirst）。
队尾插入（addLast）、队尾删除（removeLast）。
获取队头（getFirst）、获取队尾（getLast）。
实现方式：
数组实现：需处理环形逻辑（类似循环队列）。
链表实现：双向链表（便于两端操作，每个节点有prev和next指针）。
应用场景：
实现栈（用addLast和removeLast，或addFirst和removeFirst）。
滑动窗口问题（如 “滑动窗口最大值”，用 Deque 维护窗口内的候选最大值）。

public class Deque {private int[] deque;private int front; // 队头指针private int rear; // 队尾指针private int maxSize; // 队列最大容量// 初始化双端队列public Deque(int capacity) {maxSize = capacity;deque = new int[maxSize];front = 0;rear = 0;}// 判断队列是否为空public boolean isEmpty() {return front == rear;}// 判断队列是否已满public boolean isFull() {return (rear + 1) % maxSize == front;}// 队头插入public boolean addFirst(int item) {if (isFull()) {System.out.println("队列已满，无法在队头插入");return false;}front = (front - 1 + maxSize) % maxSize;deque[front] = item;return true;}// 队尾插入public boolean addLast(int item) {if (isFull()) {System.out.println("队列已满，无法在队尾插入");return false;}deque[rear] = item;rear = (rear + 1) % maxSize;return true;}// 队头删除public int removeFirst() {if (isEmpty()) {throw new RuntimeException("队列为空，无法从队头删除");}int item = deque[front];front = (front + 1) % maxSize;return item;}// 队尾删除public int removeLast() {if (isEmpty()) {throw new RuntimeException("队列为空，无法从队尾删除");}rear = (rear - 1 + maxSize) % maxSize;return deque[rear];}// 获取队头元素public int getFirst() {if (isEmpty()) {throw new RuntimeException("队列为空，无法获取队头元素");}return deque[front];}// 获取队尾元素public int getLast() {if (isEmpty()) {throw new RuntimeException("队列为空，无法获取队尾元素");}return deque[(rear - 1 + maxSize) % maxSize];}// 获取队列元素个数public int size() {return (rear - front + maxSize) % maxSize;}// 打印双端队列元素public void printDeque() {if (isEmpty()) {System.out.println("队列为空");return;}int i = front;while (i != rear) {System.out.print(deque[i] + " ");i = (i + 1) % maxSize;}System.out.println();}public static void main(String[] args) {Deque deque = new Deque(5);deque.addLast(1);deque.addLast(2);System.out.println("队尾插入 1、2 后队列：");deque.printDeque();deque.addFirst(3);System.out.println("队头插入 3 后队列：");deque.printDeque();System.out.println("队头元素：" + deque.getFirst());System.out.println("队尾元素：" + deque.getLast());deque.removeFirst();System.out.println("队头删除后队列：");deque.printDeque();deque.removeLast();System.out.println("队尾删除后队列：");deque.printDeque();}
}

其实还有一中优先级队列，博主还没有学，学出来以后再给大家讲解分享，敬请期待