当前位置：首页 > news >正文

Deep SORT：基于深度关联度量的简单在线实时跟踪

news 2025/10/13 15:12:55

SIMPLE ONLINE AND REALTIME TRACKING WITH A DEEP ASSOCIATION METRIC

摘要
引言
SORT WITH DEEP ASSOCIATION METRIC
- 轨迹处理和状态估计
- 分配问题
- 匹配级联
- 深度外观描述子
实验
结论

论文网址： DeepSORT
论文代码： DeepSORT

摘要

简单在线实时跟踪（SORT）是一种务实的多目标跟踪方法，重点在于简单而高效的算法。在本文中，我们引入了外观信息以提升 SORT 的性能。通过这一扩展，我们能够在更长时间的遮挡情况下持续跟踪目标，从而有效减少身份切换的次数。秉承原始框架的理念，我们将大部分计算复杂度放在离线预训练阶段，在该阶段，我们在一个大规模行人再识别数据集上学习一个深度关联度量。在在线应用阶段，我们通过在视觉外观空间中执行最近邻查询来建立测量与轨迹之间的关联关系。实验评估表明，我们的扩展使身份切换次数减少了 45%，并在保持高帧率的同时实现了整体上具有竞争力的性能。

引言

得益于目标检测领域的最新进展，“检测后跟踪”已成为多目标跟踪的主流范式。在此范式下，目标轨迹通常被建模为一个全局优化问题，需要一次性处理整段视频。例如，流网络形式化方法与概率图模型已成为这类框架的热门选择。然而，由于采用批处理方式，这些方法无法应用于在线场景——后者要求在每个时间步都能即时获得目标身份。

更传统的方法包括多重假设跟踪（MHT）与联合概率数据关联滤波器（JPDAF）。它们逐帧执行数据关联。JPDAF 通过将各量测按其关联似然加权，生成单一状态假设；MHT 则维护所有可能假设，但为实现计算可行性必须引入剪枝策略。最近，这两种方法在“检测后跟踪”设定下被重新审视，并展现出良好效果。然而，其性能提升伴随着更高的计算与实现复杂度。

Simple Online and Realtime Tracking（SORT）是一个更为简洁的框架：它在图像空间中进行卡尔曼滤波，并逐帧采用匈牙利算法完成数据关联，关联度量仅计算边界框的重叠程度。这一简单方法在高帧率下仍能取得优异性能。在 MOT Challenge 数据集上，SORT 配合当时的顶尖行人检测器，其平均排名甚至高于使用标准检测结果的 MHT。这不仅凸显了目标检测器性能对整体跟踪结果的关键影响，也是从实践者角度得出的重要启示。

尽管 SORT 在跟踪精度和准确性方面总体表现良好，但它产生的身份切换次数仍然偏高。原因在于，其所采用的关联度量仅在状态估计不确定性较低时才可靠；因此，SORT 在应对正面视角摄像头场景中常见的遮挡时存在明显缺陷。我们通过引入一种融合运动与外观信息的更具判别力的关联度量来解决这一问题。具体而言，我们部署了一个在大型行人重识别数据集上训练过的卷积神经网络（CNN）。集成该网络后，系统在保持易于实现、高效且适用于在线场景的同时，对漏检和遮挡的鲁棒性显著提升。我们的代码及预训练 CNN 模型已公开发布，以促进研究实验与实际应用开发。

SORT WITH DEEP ASSOCIATION METRIC

我们采用传统的单假设跟踪方法，通过递归卡尔曼滤波与逐帧数据关联实现。下一节将更详细地介绍该系统的核心组件。

轨迹处理和状态估计

轨迹处理和卡尔曼滤波框架大体上与文献中的原始方法相同。我们假设一个非常通用的跟踪场景：摄像机未经过标定，并且没有可用的自运动（ego-motion）信息。虽然这些条件对滤波框架构成了挑战，但它是近期多目标跟踪基准中最常考虑的设置。因此，我们的跟踪场景定义在八维状态空间 ((u, v, \gamma, h, \dot{x}, \dot{y}, \dot{\gamma}, \dot{h})) 上，其中包含边界框中心位置 ((u, v))、宽高比 (\gamma)、高度 (h)，以及它们在图像坐标中的各自速度。我们使用标准的卡尔曼滤波器（Kalman Filter），假设目标具有恒定速度运动并采用线性观测模型，其中将边界框的坐标 ((u, v, \gamma, h)) 直接作为目标状态的观测值。

对于每条轨迹 (k)，我们记录自上一次成功的测量关联以来经过的帧数 (a_k)。在卡尔曼滤波预测阶段，该计数器会递增；当轨迹与某个测量成功关联时，计数器会被重置为 0。超过预定义最大寿命 (A_\text{max}) 的轨迹被视为已离开场景，并从轨迹集合中删除。对于无法与现有轨迹关联的每个检测，会生成新的轨迹假设。在最初的三帧内，这些新轨迹被视为暂定（tentative）轨迹。在此期间，我们期望每一帧都能与测量成功关联。如果新轨迹在前三帧内未能成功关联到任何测量，它将被删除。

分配问题

解决预测的卡尔曼状态与新到测量之间关联的传统方法是构建一个分配问题（assignment problem），并使用匈牙利算法（Hungarian algorithm）进行求解。在这个问题的建模中，我们通过结合两种适当的度量，将运动信息和外观信息整合进去。

为了融合运动信息，我们使用预测的卡尔曼状态与新到达的测量之间的（平方）马氏距离：

$d^{(1)}(i, j) = (d_j - y_i)^T S_i^{-1} (d_j - y_i),$

其中，我们用 $y_i, S_i)$ 表示第 i 条轨迹在测量空间中的投影，用 $d_j$ 表示第 j 个边界框检测。马氏距离通过衡量检测点距离轨迹均值的位置有多少个标准差，从而考虑了状态估计的不确定性。此外，使用该度量可以通过对马氏距离进行阈值处理来排除不太可能的关联，阈值由逆 $χ2\chi^2$ 分布在 95% 置信区间下计算得出。我们用指标表示这一决策：

$bi,j(1)=1[d(1)(i,j)≤t(1)]b^{(1)}_{i,j} = 1[d^{(1)}(i, j) \le t^{(1)}]$

当第 i 条轨迹与第 j 个检测的关联是可接受时，该指标取值为 1。对于我们的四维测量空间，相应的马氏距离阈值为 $t^{(1)} = 9.4877$ 。

虽然当运动不确定性较低时，马氏距离是一个合适的关联度量，但在我们基于图像空间的问题建模中，由卡尔曼滤波框架得到的预测状态分布仅能提供目标位置的粗略估计。尤其是，未考虑的相机运动可能会在图像平面上引入快速位移，使得马氏距离在遮挡情况下的跟踪中信息量较低。因此，我们在关联问题中引入了第二种度量。

对于每个边界框检测 $d_j$ ，我们计算一个外观描述子 $r_j$ ，并归一化为 $r_j| = 1$ 。此外，我们为每条轨迹 $k$ 保存一个图库 $R_k = { r_k^{(i)} }_{i=1}^{L_k}$ ，其中包含最近 $L_k = 100$ 个关联的外观描述子。然后，我们的第二种度量在外观空间中测量第 i 条轨迹与第 j 个检测之间的最小余弦距离：

$d(2)(i,j)=min⁡1−rjTrk(i)∣rk(i)∈Ri.d^{(2)}(i, j) = \min { 1 - r_j^T r_k^{(i)} \mid r_k^{(i)} \in R_i }.$

同样，我们引入一个二值变量来表示该关联是否在此度量下是可接受的：

$bi,j(2)=1[d(2)(i,j)≤t(2)]b^{(2)}_{i,j} = 1[d^{(2)}(i, j) \le t^{(2)}]$

并且我们在一个单独的训练数据集上为该指标找到合适的阈值。在实际应用中，我们使用预训练的卷积神经网络（CNN）来计算边界框的外观描述子。该网络的架构在第 2.4 节中进行了描述。

综合来看，这两种度量互为补充，在关联问题中各司其职。一方面，马氏距离提供了基于运动的可能目标位置的信息，对于短期预测特别有用。另一方面，余弦距离考虑了外观信息，在长期遮挡后恢复目标身份时尤其有效，因为此时运动信息的区分能力较弱。

为了构建关联问题，我们将两种度量结合成加权和：

$ci,j=λd(1)(i,j)+(1−λ)d(2)(i,j)c_{i,j} = \lambda d^{(1)}(i, j) + (1 - \lambda) d^{(2)}(i, j)$

当某个关联在两种度量的门控区域内时，我们认为该关联是可接受的：

$bi,j=∏m=12bi,j(m).b_{i,j} = \prod_{m=1}^{2} b^{(m)}_{i,j}.$

每种度量对组合关联代价的影响可以通过超参数 $λ\lambda$ 来控制。在实验中，我们发现当存在显著的相机运动时，将 $λ=0\lambda = 0$ 是一个合理的选择。在这种情况下，关联代价项仅使用外观信息。然而，马氏距离的门控仍然被使用，以根据卡尔曼滤波器推断的可能目标位置排除不可行的关联。

匹配级联

我们并不是在一个全局关联问题中一次性求解测量到轨迹的关联，而是引入了一个级联方法，通过一系列子问题逐步求解。为了说明这种方法的动机，考虑以下情况：当一个目标被遮挡较长时间后，随后的卡尔曼滤波预测会增加与该目标位置相关的不确定性。因此，概率质量在状态空间中扩散，观测似然也变得不那么集中。直观上，关联度量应该通过增大测量到轨迹的距离来考虑这种概率质量的扩散。然而，反直觉的是，当两条轨迹竞争同一个检测时，马氏距离反而偏向于较大的不确定性，因为它会有效地减小任何检测点到轨迹投影均值的标准差距离。这是一种不希望出现的行为，因为它可能导致轨迹碎片增多和轨迹不稳定。因此，我们引入了一个匹配级联（matching cascade），优先处理出现频率更高的目标，以在关联似然中编码我们对概率扩散的认知。
在这里插入图片描述
列表 1 概述了我们的匹配算法。输入包括轨迹集合 $T$ 和检测集合 $D$ 的索引，以及最大年龄 $AmaxA_{\text{max}}$ 。在第 1 行和第 2 行，我们计算关联代价矩阵和可接受关联矩阵。然后，我们按轨迹年龄 $n$ 迭代，对年龄逐渐增加的轨迹求解线性分配问题。
在第 6 行，我们选择在过去 $n$ 帧中没有被关联到检测的轨迹子集 $T_n$ 。
在第 7 行，我们在轨迹 $T_n$ 与未匹配检测集合 $U$ 之间求解线性分配问题。
在第 8 行和第 9 行，我们更新匹配集合和未匹配检测集合，并在第 11 行完成后返回结果。
注意，这个匹配级联（matching cascade）优先处理年龄较小的轨迹，也就是最近出现过的轨迹。

1. “轨迹年龄”是什么？
* 轨迹在每一帧都会更新，如果一条轨迹在某一帧没找到匹配，它的“年龄”就 +1
* 年龄越小 → 最近刚被看到 → 信息更可靠
* 年龄越大 → 最近很久没匹配到检测 → 位置不确定性更大2. 级联匹配怎么做？
* 假设你有多条轨迹和多个人物检测点
* 算法先处理**年龄小的轨迹**（最近刚出现的轨迹）
* 年龄小的轨迹先挑选与检测点匹配
* 年龄大的轨迹留到后面再匹配未分配的检测点
直观理解：先让“可靠的轨迹”先选位置，减少预测不准导致的错误匹配。

在最后的匹配阶段，我们对年龄为 (n = 1) 的未确认轨迹和未匹配轨迹集合，运行原始 SORT 算法中提出的交并比（IoU）关联方法。这有助于处理突发的外观变化，例如由于静态场景几何导致的部分遮挡，同时也提高了对错误初始化的鲁棒性。

深度外观描述子

通过使用简单的最近邻查询而不进行额外的度量学习，我们的方法能够成功应用的前提是需要在离线阶段训练出区分能力良好的特征嵌入，在实际的在线跟踪前完成训练。为此，我们采用了一种在大型行人重识别（person re-identification）数据集上训练过的卷积神经网络（CNN），该数据集包含 1,261 名行人的超过 1,100,000 张图像，非常适合用于人群跟踪场景下的深度度量学习。
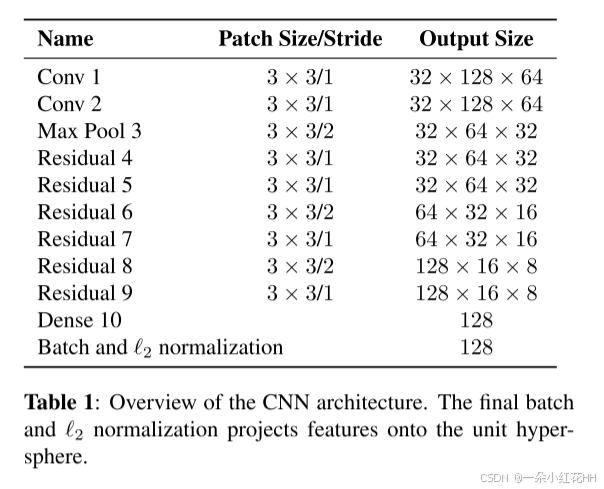
在这里插入图片描述

我们的网络 CNN 架构如表 1 所示。简而言之，我们采用了宽残差网络（Wide Residual Network） ，包含两个卷积层，随后是六个残差块（residual blocks）。在第 10 层的全连接层中计算维度为 128 的全局特征图。最后，通过批量归一化（batch normalization）和 L2 归一化将特征投影到单位超球面上，使其能够与余弦外观度量（cosine appearance metric）兼容。

总体而言，该网络有 2,800,864 个参数，处理 32 个边界框的前向推理大约需要 30 毫秒（使用 Nvidia GeForce GTX 1050 移动 GPU）。因此，只要有现代 GPU 支持，该网络非常适合在线跟踪。虽然本文不涉及具体训练细节，但我们在 GitHub 仓库中提供了预训练模型。