逻辑运算 | 位运算
注:本文为 “逻辑运算 | 位运算” 相关文章合辑。
英文引文,机翻未校。
中文引文,未整理去重。
如有内容异常,请看原文。
Understanding Bitwise Operations and Their Uses in Programming
了解按位运算及其在编程中的用途

In the world of programming, bitwise operations are powerful tools that operate directly on the binary representations of numbers. While they may seem esoteric at first, mastering bitwise operations can lead to more efficient code and unlock solutions to complex problems. This article will delve into the intricacies of bitwise operations, their various uses, and how they can be applied in real-world programming scenarios.
在编程领域,按位运算是直接对数字的二进制表示进行作的强大工具。虽然它们乍一看可能很深奥,但掌握按位运算可以带来更高效的代码并解锁复杂问题的解决方案。本文将深入探讨 bitwise 运算的复杂性、它们的各种用途,以及如何将它们应用于实际编程场景。
What Are Bitwise Operations?
什么是按位运算?
Bitwise operations are fundamental operations that work at the bit level of numbers. Instead of treating numbers as whole entities, these operations manipulate individual bits within the binary representation of those numbers. The most common bitwise operators are:
按位运算是在数字的位级工作的基本运算。这些作不是将数字视为整个实体,而是作这些数字的二进制表示形式中的单个位。最常见的按位运算符是:
- AND (&) 和 (&)
- OR (|) 或 (|)
- XOR (^) 异或 (^)
- NOT (~) 非 (~)
- Left Shift (<<) 左移 (<<)
- Right Shift (>>) 右移 (>>)
Let’s explore each of these operators in detail.
让我们详细探讨一下这些运算符中的每一个。
1. Bitwise AND (&)
- 按位 AND (&)
The bitwise AND operator compares each bit of two numbers and returns 1 if both bits are 1, otherwise it returns 0. This operation is often used for masking or checking if a particular bit is set.
按位 AND 运算符比较两个数字的每个位,如果两个位都为 1,则返回 1,否则返回 0。此作通常用于屏蔽或检查是否设置了特定位。
1010 (10 in decimal)
& 1100 (12 in decimal)
----
1000 (8 in decimal)
2. Bitwise OR (|)
- 按位 OR (|)
The bitwise OR operator compares each bit of two numbers and returns 1 if at least one of the bits is 1, otherwise it returns 0. This operation is commonly used for combining flags or setting specific bits.
按位 OR 运算符比较两个数字的每个位,如果至少有一个位为 1,则返回 1,否则返回 0。此作通常用于组合标志或设置特定位。
1010 (10 in decimal)
| 1100 (12 in decimal)
----
1110 (14 in decimal)
3. Bitwise XOR (^)
- 按位 XOR (^)
The bitwise XOR (exclusive OR) operator compares each bit of two numbers and returns 1 if the bits are different, otherwise it returns 0. XOR has interesting properties that make it useful for various operations, including simple encryption and toggling bits.
按位 XOR(异或)运算符比较两个数字的每个位,如果位不同,则返回 1,否则返回 0。XOR 具有有趣的属性,使其可用于各种作,包括简单的加密和切换位。
1010 (10 in decimal)
^ 1100 (12 in decimal)
----
0110 (6 in decimal)
4. Bitwise NOT (~)
- 按位 NOT (~)
The bitwise NOT operator inverts all the bits of a number, changing 0s to 1s and vice versa. It’s important to note that the result depends on the number of bits used to represent the number in your system.
按位 NOT 运算符反转数字的所有位,将 0 更改为 1,反之亦然。请务必注意,结果取决于系统中用于表示数字的位数。
~ 1010 (10 in decimal)
----
0101 (5 in decimal, assuming 4-bit representation)
5. Left Shift (<<)
- 左移 (<<)
The left shift operator moves all bits in a number to the left by a specified number of positions. This operation effectively multiplies the number by 2 raised to the power of the shift amount.
左移运算符将数字中的所有位向左移动指定数量的位置。此作有效地将数字乘以 2 的 次幂 shift 量。
1010 << 1
----
10100 (20 in decimal)
6. Right Shift (>>)
- 右移 (>>)
The right shift operator moves all bits in a number to the right by a specified number of positions. This operation effectively divides the number by 2 raised to the power of the shift amount (for positive numbers).
右移运算符将数字中的所有位向右移动指定数量的位置。此作有效地将数字除以 2 的 Shift 量的幂(对于正数)。
1010 >> 1
----
0101 (5 in decimal)
Practical Applications of Bitwise Operations
按位运算的实际应用
Now that we’ve covered the basics of bitwise operations, let’s explore some practical applications where these operations shine.
现在我们已经介绍了按位运算的基础知识,让我们探索这些运算大放异彩的一些实际应用。
1. Efficient Multiplication and Division
1.高效的乘法和除法
Left and right shift operations can be used for quick multiplication and division by powers of 2. This is often faster than traditional multiplication and division operations.
左移和右移作可用于快速乘以和除以 2 的幂。这通常比传统的乘法和除法运算更快。
// Multiply by 2
int multiplyByTwo(int n) {
return n << 1;
}
// Divide by 2
int divideByTwo(int n) {
return n >> 1;
}
2. Checking Even/Odd Numbers
2.检查偶数/奇数
The bitwise AND operator can be used to efficiently check if a number is even or odd.
按位 AND 运算符可用于有效地检查数字是偶数还是奇数。
boolean isEven(int n) {
return (n & 1) == 0;
}
3. Swapping Variables Without a Temporary Variable
3.在没有临时变量的情况下交换变量
XOR can be used to swap two variables without using a temporary variable:
XOR 可用于交换两个变量,而无需使用临时变量:
void swapWithoutTemp(int &a, int &b) {
a = a ^ b;
b = a ^ b;
a = a ^ b;
}
4. Setting, Clearing, and Toggling Bits
4.设置、清除和切换位
Bitwise operations are perfect for manipulating individual bits:
按位运算非常适合处理单个位:
// Set the nth bit
int setBit(int num, int n) {
return num | (1 << n);
}
// Clear the nth bit
int clearBit(int num, int n) {
return num & ~(1 << n);
}
// Toggle the nth bit
int toggleBit(int num, int n) {
return num ^ (1 << n);
}
5. Bit Masking
5.位掩码
Bit masking is a technique used to extract or manipulate specific bits within a number. It’s commonly used in graphics programming, network protocols, and embedded systems.
位掩码是一种用于提取或作数字中特定位的技术。它通常用于图形编程、网络协议和嵌入式系统。
// Extract the last 4 bits of a number
int extractLastFourBits(int num) {
return num & 0xF; // 0xF is 1111 in binary
}
6. Efficient Power of 2 Checking
6.2 次检查的高效功能
Bitwise operations can be used to efficiently check if a number is a power of 2:
按位运算可用于有效地检查数字是否为 2 的幂:
boolean isPowerOfTwo(int n) {
return n > 0 && (n & (n - 1)) == 0;
}
Advanced Bitwise Techniques
高级 Bitwise 技术
As we delve deeper into bitwise operations, we encounter more advanced techniques that can significantly optimize certain algorithms and solve complex problems efficiently.
随着我们对按位运算的深入研究,我们会遇到更先进的技术,这些技术可以显著优化某些算法并有效地解决复杂问题。
1. The Brian Kernighan Algorithm
1.Brian Kernighan 算法
This algorithm is used to count the number of set bits (1s) in a binary number efficiently:
此算法用于有效地计算二进制数中的设置位 (1) 的数量:
int countSetBits(int n) {
int count = 0;
while (n) {
n &= (n - 1);
count++;
}
return count;
}
This algorithm works by repeatedly turning off the rightmost set bit until the number becomes zero.
此算法的工作原理是反复关闭最右侧的设置位,直到数字变为零。
2. Finding the Rightmost Set Bit
2.找到最正确的 Set Bit
To find the position of the rightmost set bit in a number:
要查找数字中最右边的 set bit 的位置:
int findRightmostSetBit(int n) {
return log2(n & -n) + 1;
}
This uses the property that for any integer n, n & -n gives a number with only the rightmost set bit of n.
这使用了这样一个属性:对于任何整数 n, n & -n 都给出一个只有最右边的 n 集合位的数字。
3. XOR Properties for Solving Unique Element Problems
3.用于解决独特单元问题的 XOR 属性
XOR has some interesting properties that make it useful for solving problems involving finding unique elements:
XOR 具有一些有趣的属性,使其可用于解决涉及查找唯一元素的问题:
-
XOR of a number with itself is 0
数字与自身的 XOR 为 0 -
XOR of a number with 0 is the number itself
值为 0 的数字的 XOR 是数字本身 -
XOR is associative and commutative
XOR 是结合和交换的
These properties can be used to solve problems like finding the single non-repeating element in an array where every other element appears twice:
这些属性可用于解决诸如在数组中查找每个其他元素出现两次的单个非重复元素等问题:
int findSingleElement(int arr[], int n) {
int result = 0;
for (int i = 0; i < n; i++) {
result ^= arr[i];
}
return result;
}
4. Gray Code
4.格雷码
Gray code is a sequence of numbers where adjacent numbers differ by only one bit. It can be generated using bitwise operations:
格雷码是相邻数字仅相差一位的数字序列。它可以使用按位运算生成:
int grayCode(int n) {
return n ^ (n >> 1);
}
5. Bitwise Operations in Cryptography
5.密码学中的按位运算
Bitwise operations play a crucial role in many cryptographic algorithms. For example, the XOR operation is often used in simple encryption techniques:
按位运算在许多加密算法中起着至关重要的作用。例如,XOR作通常用于简单的加密技术中:
string xorEncrypt(string text, char key) {
string result = text;
for (int i = 0; i < text.length(); i++) {
result[i] = text[i] ^ key;
}
return result;
}
// Decryption is the same operation
string xorDecrypt(string encryptedText, char key) {
return xorEncrypt(encryptedText, key);
}
Bitwise Operations in Different Programming Languages
不同编程语言中的按位运算
While the concepts of bitwise operations remain the same across programming languages, the syntax and some specific behaviors may vary. Let’s look at how bitwise operations are implemented in some popular programming languages:
虽然按位运算的概念在编程语言中保持不变,但语法和某些特定行为可能会有所不同。让我们看看一些流行的编程语言是如何实现按位运算的:
C/C++
C and C++ provide direct support for all bitwise operators:
C 和 C++ 直接支持所有按位运算符:
#include <iostream>
using namespace std;
int main() {
int a = 5, b = 3;
cout << "AND: " << (a & b) << endl;
cout << "OR: " << (a | b) << endl;
cout << "XOR: " << (a ^ b) << endl;
cout << "NOT: " << (~a) << endl;
cout << "Left Shift: " << (a << 1) << endl;
cout << "Right Shift: " << (a >> 1) << endl;
return 0;
}
Python
Python also supports all bitwise operators, but uses different symbols for some operations:
Python 还支持所有按位运算符,但对某些作使用不同的符号:
a, b = 5, 3
print(f"AND: {a & b}")
print(f"OR: {a | b}")
print(f"XOR: {a ^ b}")
print(f"NOT: {~a}")
print(f"Left Shift: {a << 1}")
print(f"Right Shift: {a >> 1}")
Java
Java’s bitwise operators are similar to C/C++:
Java 的按位运算符类似于 C/C++:
public class BitwiseDemo {
public static void main(String[] args) {
int a = 5, b = 3;
System.out.println("AND: " + (a & b));
System.out.println("OR: " + (a | b));
System.out.println("XOR: " + (a ^ b));
System.out.println("NOT: " + (~a));
System.out.println("Left Shift: " + (a << 1));
System.out.println("Right Shift: " + (a >> 1));
}
}
JavaScript
JavaScript supports bitwise operations, but it’s important to note that all numbers in JavaScript are floating-point, so bitwise operations convert them to 32-bit integers:
JavaScript 支持按位运算,但需要注意的是,JavaScript 中的所有数字都是浮点运算,因此按位运算会将它们转换为 32 位整数:
let a = 5, b = 3;
console.log("AND:", a & b);
console.log("OR:", a | b);
console.log("XOR:", a ^ b);
console.log("NOT:", ~a);
console.log("Left Shift:", a << 1);
console.log("Right Shift:", a >> 1);
console.log("Unsigned Right Shift:", a >>> 1);
Note that JavaScript has an additional unsigned right shift operator (>>>) that always fills with zeros.
请注意,JavaScript 有一个额外的无符号右移运算符 (>>>),它总是用零填充。
Performance Considerations
性能注意事项
While bitwise operations can lead to more efficient code in many cases, it’s important to consider the context and potential trade-offs:
虽然在许多情况下,按位运算可以带来更高效的代码,但重要的是要考虑上下文和可能的权衡:
Advantages:
优势:
- Speed: Bitwise operations are typically faster than their arithmetic counterparts, especially for simple operations like multiplication or division by powers of 2.
速度:按位运算通常比算术运算更快,尤其是对于乘法或除以 2 的幂等简单运算。 - Memory efficiency: Bitwise operations can be used to pack multiple boolean flags into a single integer, saving memory.
内存效率:按位运算可用于将多个布尔标志打包成一个整数,从而节省内存。 - Low-level control: They provide fine-grained control over individual bits, which is crucial in areas like embedded systems and device drivers.
低级控制:它们提供对单个位的精细控制,这在嵌入式系统和设备驱动程序等领域至关重要。
Considerations:
考虑:
- Readability: Code using bitwise operations can be less intuitive and harder to maintain if not well-documented.
可读性:如果没有充分的文档记录,使用按位运算的代码可能不太直观且更难维护。 - Portability: The behavior of bitwise operations, especially with signed integers, can vary across different systems and languages.
可移植性:按位运算的行为(尤其是有符号整数)可能因不同的系统和语言而异。 - Optimization: Modern compilers are often capable of optimizing arithmetic operations to use bitwise operations where appropriate, so manual optimization may not always be necessary.
优化:现代编译器通常能够优化算术运算,以便在适当时使用按位运算,因此可能并不总是需要手动优化。
Common Pitfalls and Best Practices
常见陷阱和最佳实践
When working with bitwise operations, be aware of these common pitfalls and follow these best practices:
使用按位运算时,请注意这些常见陷阱并遵循以下最佳实践:
Pitfalls:
陷阱:
-
Sign extension: Be careful with right shifts on signed integers, as the behavior can be platform-dependent.
符号扩展:请小心对有符号整数的右移,因为其行为可能取决于平台。 -
Overflow: Left shifts can easily cause overflow, especially when shifting by large amounts.
溢出:左移很容易导致溢出,尤其是在大量移位时。 -
Precedence: Bitwise operators often have lower precedence than arithmetic operators. Use parentheses to ensure correct order of operations.
优先级:按位运算符的优先级通常低于算术运算符。使用括号确保作顺序正确。
Best Practices:
最佳实践:
- Use constants: Define named constants for bit masks to improve readability.
Use constants(使用常量):定义位掩码的命名常量以提高可读性。 - Comment your code: Clearly explain the purpose and logic behind complex bitwise operations.
注释您的代码:清楚地解释复杂按位运算背后的目的和逻辑。 - Test thoroughly: Bitwise operations can be tricky, so ensure comprehensive testing, especially for edge cases.
彻底测试:按位运算可能很棘手,因此请确保全面测试,尤其是对于边缘情况。 - Consider alternatives: Sometimes, using standard arithmetic or boolean operations might be clearer and just as efficient.
考虑替代方案:有时,使用标准算术或布尔运算可能更清晰且同样有效。
Conclusion
结论
Bitwise operations are powerful tools in a programmer’s arsenal. They offer efficiency and elegance in solving certain types of problems, particularly in areas like low-level system programming, optimization, and algorithm design. While they may seem daunting at first, with practice and understanding, bitwise operations can become an invaluable part of your coding toolkit.
As you continue to develop your programming skills, remember that mastering bitwise operations is just one aspect of becoming a proficient coder.
按位运算是程序员武器库中的强大工具。它们在解决某些类型的问题时提供了效率和优雅,尤其是在低级系统编程、优化和算法设计等领域。虽然它们乍一看似乎令人生畏,但通过实践和理解,按位运算可以成为您编码工具包中非常宝贵的部分。随着您继续发展编程技能,请记住,掌握按位运算只是成为熟练编码人员的一个方面。
Bitwise Operations
按位运算
Bitwise operations are a set of operations on binary strings (also known as bit strings) that will evaluate and manipulate individual bits of their inputs sequentially. These operators are implemented in most high level programming languages and CPU instruction set architectures, having a wide range of use cases and being incredibly important for manipulating data at the bit level. Here, we will cover the most notable bitwise operators, explaining how they work and their applications.
按位运算是对二进制字符串(也称为位串)的一组运算,这些运算将按顺序计算和作其输入的各个位。这些运算符在大多数高级编程语言和 CPU 指令集架构中实现,具有广泛的用例,对于在位级别处理数据非常重要。在这里,我们将介绍最著名的按位运算符,解释它们的工作原理和应用。
Bitwise AND
按位 AND
Provided two equal length bit strings, the bitwise AND will perform the logical AND on each bit in the bit strings. For each bit position, if both binary strings contain a 1 in that position, AND will return a 1. Otherwise, AND returns 0 in that position.
提供两个相等长度的位字符串,按位 AND 将对位字符串中的每个位执行逻辑 AND。对于每个位位置,如果两个二进制字符串在该位置都包含 1,则 AND 将返回 1。否则,AND 在该位置返回 0。

Programming languages will typically implement bitwise AND with the & operator (distinct from &&) which supports operations over integers. Consider the following Python snippet:
编程语言通常使用 & 运算符(不同于 &&)实现按位 AND,该运算符支持对整数进行运算。请考虑以下 Python 代码段:
a = 0b100 # 4 represented in binary
b = 0b110 # 6 represented in binary
print(bin(a & b))
Bitwise OR
按位 OR
Bitwise OR will perform logical OR on each bit, returning 1 if there is a 1 in either input for each bit position, returning 0 otherwise.
按位 OR 将在每个位上执行逻辑 OR,如果每个位位置的任一输入中有 1,则返回 1,否则返回 0。

Languages typically implement OR with the | operator (distinct from ||) used on integer operations:
语言通常使用用于整数运算的 | 运算符(不同于 ||)实现 OR:
a = 0b100
b = 0b110
print(bin(a | b))
Bitwise XOR
按位 XOR
XOR will perform a logical XOR on each bit, returning 1 if one and only one input contains a 1 in a position, returning 0 otherwise.
XOR 将在每个位上执行逻辑 XOR,如果一个且只有一个输入在某个位置包含 1,则返回 1,否则返回 0。

XOR is implemented with the ^ operator in most languages:
XOR 在大多数语言中使用 ^ 运算符实现:
a = 0b100
b = 0b110
print(bin(a ^ b))
Bitwise NOT 按位 NOT
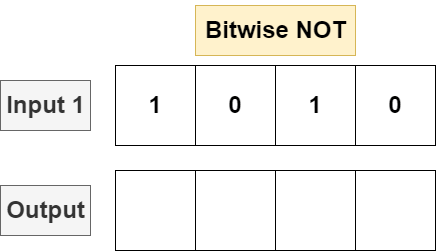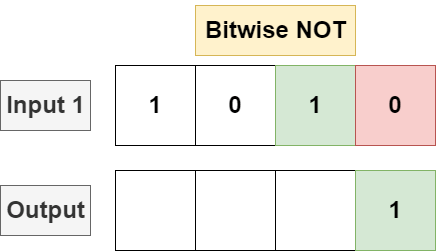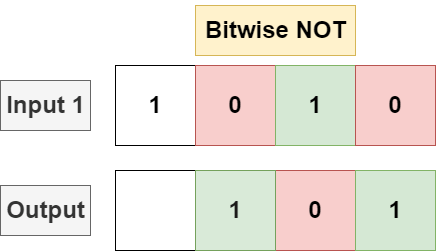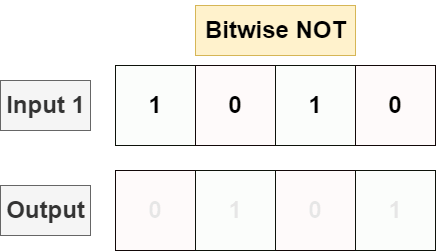
Given a single input bitstring, bitwise NOT will invert every single bit in the bit string, flipping each 1 to a 0 and vice versa.
给定单个输入位串,按位 NOT 将反转位串中的每个位,将每个 1 翻转为 0,反之亦然。
Programming languages typically implement NOT with the ~ operator:
编程语言通常使用 ~ 运算符实现 NOT:
a = 0b100
print(bin(~a))
Bit shifting
位移位
Most programming languages implement two operators for performing bit shifts. Given a bit string and a number n, the left bit shift << will shift a bitstring n bits to the left. If the appending a 0 byte in the least significant (leftmost) position each shift. For programming languages where the underlying data type of the bit string has a fixed byte length, a left bit shift will discard the most significant (right most) bit in the string. The following example is a bit shift executed on an unsigned 4 bit number.
大多数编程语言都实现了两个运算符来执行移位。给定一个位串和一个数字 n,左移位 << 会将位串 n 位向左移位。如果在每个班次的最低有效(最左侧)位置附加一个 0 字节。对于位字符串的基础数据类型具有固定字节长度的编程语言,左移位将丢弃字符串中最高有效(最右边)的位。以下示例是对无符号 4 位数字执行的移位。

The right bit shift will move every bit in the string n bits to the right, discarding the least significant bit in the bit string and appending a 0 in the most significant position. If the input bit string is a signed data type and the sign bit is set to 1 (meaning the input is negative), then some implementations will insert a 1 in the most significant position to leave the operand negative, but this is not universal. The following is a bit shift on an unsigned 4 bit number.
右移位会将字符串 n 位中的每个位向右移动,丢弃位字符串中最低有效位,并在最高有效位置附加 0。如果 input bit string 是有符号数据类型并且 sign bit 设置为 1 (意味着 input 为负数),则某些实现将在最高有效位置插入 1 以使作数为负数,但这并不是通用的。以下是无符号 4 位数字的位移。

Bit shifting is implemented with the << (for left shift) and >> (for right shift) operators:
移位是通过 << (左移) 和 >> (右移) 运算符实现的:
a = 0b110
print(bin(a >> 2))
b = 0b1
print(bin(b << 3))
Applications of bitwise operations
按位运算的应用
Operations on bit-based data structures
对基于位的数据结构的作_.
Many data structures can be represented purely as a string of bits, meaning that they can easily be manipulated by bitwise operations. The the most notable examples of bit-level data structures are bit fields. and bitmaps., and both representations are easily modifiable and queryable via bitwise operations.
许多数据结构可以纯粹表示为一串位,这意味着它们可以很容易地通过按位运算进行作。位级数据结构最显著的示例是位字段和位图,这两种表示形式都可以通过按位作轻松修改和查询。
Optimizing multiplication with bit shifts
使用移位优化乘法
In many cases, bitwise operations can be significantly faster ways to perform certain mathematical operations instead of standard arithmetic at the CPU instruction level. Many compilers take advantage of this idea, and will have compiled binaries execute bit shifts instead of multiplication operations where doing so would optimize program runtime. In specific, we can take advantage of the idea that a left bit shift is the same as multiplying by 2 to speed up our program. Let’s consider a small C program running on an x86 instruction set:
在许多情况下,按位运算是执行某些数学运算而不是 CPU 指令级别的标准算术的更快方法。许多编译器利用了这个想法,并且会让编译后的二进制文件执行移位而不是乘法运算,这样做会优化程序运行时。具体来说,我们可以利用左移位等同于乘以 2 的想法来加快我们的程序。让我们考虑一个在 x86 指令集上运行的小型 C 程序:
int a = 2;
a = a * 16;
At first guess, we would expect this program to execute some multiplication instruction (in the case of x86, the instruction would be mul or imul), but if we decompile the binary of this program with objdumb -d, we can see that our program is actually using shl (x86’s left bit shift instruction) to do the multiplication!
乍一猜测,我们期望这个程序执行一些乘法指令(在 x86 的情况下,指令会是 mul 或 imul),但是如果我们用 objdumb -d 反编译这个程序的二进制文件,我们可以看到我们的程序实际上是在使用 shl(x86 的左移位指令)来做乘法!
0000000000001129 <main>:
1129: f3 0f 1e fa endbr64
112d: 55 push %rbp
112e: 48 89 e5 mov %rsp,%rbp
1131: c7 45 fc 02 00 00 00 movl $0x2,-0x4(%rbp) ; int a = 2 occurs here.
1138: c1 65 fc 04 shll $0x4,-0x4(%rbp) ; left shift executed here!
113c: b8 00 00 00 00 mov $0x0,%eax
1141: 5d pop %rbp
1142: c3 retq
1143: 66 2e 0f 1f 84 00 00 nopw %cs:0x0(%rax,%rax,1)
114a: 00 00 00
114d: 0f 1f 00 nopl (%rax)
The reason why our program ultimately uses shll instead of simply multiplying the two numbers is because x86’s bit shift instruction runs significantly faster than a multiplication instruction. The compiler leverages the fact that we can very easily multiply a by 16 by instead bit shifting it by 4 instead, and runs the faster instruction.
我们的程序最终使用 shll 而不是简单地将两个数字相乘的原因是 x86 的移位指令比乘法指令运行得快得多。编译器利用了这样一个事实,即我们可以很容易地将 a 乘以 16,而是将其移位为 4,并运行更快的指令。
That said, using bit shifts in high-level source code generally does not provide a unique performance boost. For compiled languages, what instructions the CPU executes is determined by the compiler, and the level and form of optimization can vary wildly depending system architecture and the specific compiler that is used. In practical terms, this means that using bit shifts over multiplication is a readability concern instead of a performance concern, and programmers should not use bit shifts in place of multiplication to achieve performance.
也就是说,在高级源代码中使用移位通常不会提供独特的性能提升。对于编译语言,CPU 执行的指令由编译器决定,优化的级别和形式可能会因系统架构和所使用的特定编译器而有很大差异。实际上,这意味着在乘法上使用 bits shift 是一个可读性问题,而不是一个性能问题,程序员不应该使用 bits shift 来代替乘法来提高性能。
讨论 1:What are the advantages of using bitwise operations? [closed]
使用按位运算有什么好处?[已关闭]
Asked 14 years, 4 months ago
Modified 11 years, 3 months ago
Closed 10 years ago. 10 年前关闭。
Following reading the latest CodeProject newsletter, I came across this article on bitwise operations. It makes for interesting reading, and I can certainly see the benefit of checking if an integer is even or odd, but testing if the n-th bit is set? What can possibly be the advantages of this?
在阅读了最新的 CodeProject 时事通讯后,我看到了这篇关于按位运算的文章。它使阅读变得有趣,我当然可以看到检查整数是偶数还是奇数的好处,但测试是否设置了第 n 位呢?这样做可能有什么好处呢?
edited Nov 15, 2011 at 14:09 Thomas Owens
asked Oct 22, 2010 at 9:51 billy.bob
1. 嵌入式系统中硬件寄存器编程
Bitwise operations are absolutely essential when programming hardware registers in embedded systems. For example every processor that I have ever used has one or more registers (usually a specific memory address) that control whether an interrupt is enabled or disabled. To allow an interrupt to fire the usual process is to set the enable bit for that one interrupt type while, most importantly, not modifying any of the other bits in the register.
在嵌入式系统中对硬件寄存器进行编程时,位运算绝对至关重要。例如,我用过的每一个处理器都有一个或多个寄存器(通常是一个特定的内存地址),用于控制中断是启用还是禁用。要允许一个中断触发,通常的过程是设置该中断类型的使能位,同时最重要的是,不修改寄存器中的任何其他位。
2. 中断源快速解码
When an interrupt fires it typically sets a bit in a status register so that a single service routine can determine the precise reason for the interrupt. Testing the individual bits allows for a fast decode of the interrupt source.
当一个中断触发时,它通常会在状态寄存器中设置一位,以便单个服务程序能够确定中断的确切原因。测试各个位可以快速解码中断源。
3. 节省内存空间:
In many embedded systems the total RAM available may be 64, 128 or 256 BYTES (that is Bytes not kilobytes or megabytes) In this environment it is common to use one byte to store multiple data items, boolean flags etc. and then use bit operations to set and read these.
在许多嵌入式系统中,可用的总随机存取存储器(RAM)可能是64、128或256字节(这里是字节,不是千字节或兆字节)。在这种环境下,通常用一个字节存储多个数据项、布尔标志等,然后使用位运算来设置和读取这些内容。
4. 数据打包与解包
I have, for a number of years been working with a satellite communications system where the message payload is 10.5 bytes. To make the best use of this data packet the information must be packed into the data block without leaving any unused bits between the fields. This means making extensive use of bitwise and shift operators to take the information values and pack them into the payload being transmitted.
多年来,我一直在研究一个卫星通信系统,其消息有效载荷为10.5字节。为了充分利用这个数据包,信息必须打包到数据块中,字段之间不能有任何未使用的位。这意味着要广泛使用位运算和移位运算符,将信息值打包到正在传输的有效载荷中。
5. 速度优势:
Basically, you use them due to size and speed considerations. Bitwise operations are incredibly simple and thus usually faster than arithmetic operations. For example to get the green portion of an rgb value, the arithmetic approach is (rgb / 256) % 256. With bitwise operations you would do something as (rgb >> 8) & 0xFF. The latter is significantly faster and once you’re used to it, its also easier. Generally bitwise operations come into play a lot when you need to encode/decode data in a compact and fast way.
基本上,由于空间和速度的考虑,你会使用位运算。位运算非常简单,因此通常比算术运算更快。例如,要获取RGB值中的绿色部分,算术方法是(rgb / 256) % 256。使用位运算,你可以这样做(rgb >> 8) & 0xFF。后者明显更快,而且一旦你习惯了,也会更容易。一般来说,当你需要以紧凑快速的方式对数据进行编码/解码时,位运算就会发挥很大作用。
6. 视频和音频编解码器应用
Bitwise operations are also used frequently in video and audio codecs, for the same reason as in embedded electronics; being able to pack five flags and an eleven bit timer into half an int is very useful when you want to make a super-efficient video codec.
位运算在视频和音频编解码器中也经常使用,原因与在嵌入式电子设备中相同;当你想要制作一个超级高效的视频编解码器时,能够将五个标志和一个11位定时器打包到半个整数中非常有用。
7. MPEG 4编码应用:
In fact, MPEG 4 even uses exponential Golomb encoding for variable-bit-length fields. A value that was 17 or 19 bits wide last packet might be only three or five bits wide this packet - and you’d figure all that out with bitwise operations.
事实上,MPEG 4甚至对可变比特长度的字段使用指数哥伦布编码。上一个数据包中宽度为17或19位的值,在这个数据包中可能只有3或5位宽 —— 而你可以通过位运算来弄清楚所有这些。
8. SIMD单元编程
It is useful when programming SIMD units, especially if the CPU’s architecture intentionally left out some SIMD instructions because they could be emulated by a few others.
在位运算在对单指令多数据(SIMD)单元进行编程时很有用,特别是当CPU架构有意省略某些SIMD指令,因为这些指令可以通过其他一些指令模拟实现时。
9. 模拟缺失指令
For example, the architecture may not define any instructions for taking the negative values of a group of 16 bytes, but that can be emulated by bitwise negating and then adding 1. Likewise, subtraction can be omitted too, because it can be emulated by taking the negative of the second operand. The availability of the “alternate route” is the reason for omitting certain instructions.
例如,架构可能没有定义任何用于获取一组16字节负值的指令,但这可以通过按位取反然后加1来模拟实现。同样,减法也可以省略,因为它可以通过取第二个操作数的负值来模拟。有 “替代方法” 可用是省略某些指令的原因。
10. 模拟更宽元素运算
Likewise, the SIMD may only support parallel 8-bit addition, without implementing addition for wider elements such as 16-bit, 32-bit or 64-bit. To emulate them, one needs to extract the sign bit from the 8-bit calculation result, then perform the carry operation on the next element.
同样,SIMD可能只支持并行8位加法,而没有实现对更宽元素(如16位、32位或64位)的加法运算。要模拟这些运算,需要从8位计算结果中提取符号位,然后对下一个元素执行进位操作。
11. 其他优势总结
Packing data, quicker ops (multiplication, division, and modulus are significantly faster if aligned to powers of 2), bit flipping, etc. Learn them and start using them and you’ll slowly start to see most of the advantages on your own.
数据打包、更快的运算(如果与2的幂对齐,乘法、除法和取模运算会明显更快)、位翻转等。学习并开始使用位运算,你会逐渐自己发现它们的大部分优势。
讨论 2
Why is addition as fast as bit-wise operations in modern processors?
为什么在现代处理器中加法和按位运算一样快?
Asked 7 years, 9 months ago
Modified 6 years, 7 months ago
I know that bit-wise operations are so fast on modern processors, because they can operate on 32 or 64 bits on parallel, so bit-wise operations take only one clock cycle. However addition is a complex operation that consists of at least one and possibly up to a dozen bit-wise operations, so I naturally thought it will be 3-4 times slower. I was surprised to see after a simple benchmark that addition is exactly as fast as any of the bit-wise operations(XOR, OR, AND etc). Can anyone shed light on this?
我知道现代处理器上的按位运算非常快,因为它们可以并行处理 32 位或 64 位运算,因此按位运算只需要一个 clock cycle。然而,加法是一个复杂的作,由至少一个甚至可能多达十几个位作组成,所以我自然认为它会慢 3-4 倍。我惊讶地发现,在一个简单的基准测试之后,加法的速度与任何按位运算(XOR、OR 等)完全相同。谁能解释一下这个?
edited May 29, 2017 at 17:27
asked May 23, 2017 at 23:44
Teodor Dyakov
1. CPU设计优化加法运算
Addition is fast because CPU designers have put in the circuitry needed to make it fast. It does take significantly more gates than bitwise operations, but it is frequent enough that CPU designers have judged it to be worth it. See https://en.wikipedia.org/wiki/Adder_(electronics).
加法运算速度快是因为CPU设计者设计了专门的电路来加速它。加法运算所需的逻辑门数量明显多于位运算,但由于其使用频率很高,CPU设计者认为这样的设计是值得的。可参考https://en.wikipedia.org/wiki/Adder_(electronics)。
2. 时钟周期与执行速度的关系
Processors are clocked, so even if some instructions can clearly be done faster than others, they may well take the same number of cycles.
处理器按固定时钟周期运行,所以即使某些指令明显比其他指令执行得更快,它们也可能花费相同数量的时钟周期。
3. 微架构对运算速度测量的影响
Nowadays, processors tend to be pipelined, multi-scalar, with out-of-order execution and whatever else. That means that they are able to execute several instructions at the same time, at various stage of completion. If you want to show by measurements that an operation takes more time that another, you have to take take those aspect in consideration as their goal is to hide those difference. You may very well have the same throughput for addition and bitwise operations when using independent data but a measure of the latency or introducing dependencies between the operations may show otherwise. And you have also to be sure that the bottleneck of your measure is in the execution, and not for instance in the memory accesses.
如今,处理器通常采用流水线、超标量以及乱序执行等技术。这意味着它们能够同时在不同的完成阶段执行多条指令。如果你想通过测量表明一种运算比另一种运算花费更多时间,就必须考虑这些因素,因为这些技术的目的就是隐藏这些差异。当使用独立数据时,加法运算和位运算的吞吐量可能相同,但测量延迟或引入运算之间的依赖关系时,结果可能会有所不同。此外,你还必须确保测量的瓶颈在于运算执行本身,而不是例如内存访问。
4. 关键路径与时钟周期的关系
The duration of a cycle is determined by the longest critical path. Basically, it’s the longest amount of time necessary for some stage of the pipline to complete. If you want to make the CPU faster, you need to optimize the critical path. If reducing the critical path per se is not possible, it can be split into 2 stages of the pipeline, and you are now able to clock your CPU at almost twice the frequency (assuming there is not another critical path that prevents you from doing this). But this comes with an overhead: you need to insert a register between the stages of the pipeline. Which means that you don’t really gain 2x speed (the register needs time to store the data), and you have complicated the whole design.
时钟周期的时长由最长的关键路径决定。基本上,它是流水线中某个阶段完成所需的最长时间。如果你想让CPU运行得更快,就需要优化关键路径。如果无法直接缩短关键路径,可以将其拆分为流水线的两个阶段,这样你就能够将CPU的时钟频率提高近一倍(前提是不存在其他关键路径阻碍你这样做)。但这会带来额外开销:你需要在流水线的两个阶段之间插入一个寄存器。这意味着你实际上并没有获得两倍的速度提升(因为寄存器存储数据需要时间),而且还使整个设计变得更加复杂。
5. 高效加法运算方法及应用
There are already quite efficient methods for performing addition (e.g. carry lookahead adders) and addition is not a critical path for the processor speed, thus is makes no sense splitting it into multiple cycles.
已经有相当高效的加法运算方法(例如超前进位加法器),并且加法运算不是影响处理器速度的关键路径,因此将其拆分成多个时钟周期没有意义。
6. 指令重要性及处理器设计平衡
Add and subtract are so common operations that you want to be able to execute them in a single cycle. As a result, it doesn’t matter that AND, OR etc. could execute faster: They still need that one cycle.
加法和减法是非常常用的运算,人们希望它们能在单个时钟周期内执行。因此,即使与、或等运算可以执行得更快也没有关系,它们仍然需要一个时钟周期。
7. 加法运算的本质
Yes: integer addition is a bitwise operation (with a few more bits than the others, but still). There is no need to do anything in stages, there is no need for complicated algorithms, clocks or anything else.
没错,整数加法本身就是一种位运算(只是涉及的位数比其他位运算略多,但本质仍是位运算)。进行整数加法运算时,无需分阶段进行,也不需要复杂的算法、时钟或其他额外的东西。
8. 不同指令集架构下指令执行周期
Especially CPUs with rich instruction sets (google CISC vs. RISC) can easily take more than one cycle for even simple commands. With interleaving, even simples commands might break down into fetch-exec-store with 3 clocks (as an example).
特别是那些具有复杂指令集的CPU(可搜索“CISC与RISC”了解更多),即使是简单的指令也可能需要多个时钟周期才能执行完成。在指令交错执行的情况下,简单指令甚至可能会分解为取指、执行、存储三个步骤,每个步骤各占一个时钟周期(这只是一个示例)。
9. 加法运算在硬件实现上的特点
No, integer addition is a simple operation; subtraction as well. It is very easy to implement adders in full hardware, and they do their stuff as instantaneously as basic bit operations.
不,整数加法是一种简单的运算,减法也是。在硬件层面完全实现加法器是非常容易的,并且加法器执行运算的速度和基本位运算一样快。
位运算全面总结
HeZephyr已于 2024 - 07 - 28 14:18:32 修改
1 位运算概述
我们知道,计算机中的数在内存中都是以二进制形式进行存储的 ,而位运算就是直接对整数在内存中的二进制位进行操作,因此其执行效率非常高,在程序中尽量使用位运算进行操作,这会大大提高程序的性能。

那么,涉及位运算的运算符如下表所示:
| 符号 | 描述 | 运算规则 | 实例(以四位二进制数为例) |
|---|---|---|---|
| & \& & | 与 | 两个位都为 1 1 1 时,结果才为 1 1 1。 | 0001 & 0001 = 1 , 0001 & 0000 = 0 , 0000 & 0000 = 0000 0001 \& 0001 = 1, 0001 \& 0000 = 0, 0000 \& 0000 = 0000 0001&0001=1,0001&0000=0,0000&0000=0000 |
| ∣ \mid ∣ | 或 | 两个位都为 0 0 0 时,结果才为 0 0 0。 | 0001 ∣ 0001 = 0001 , 0001 ∣ 0000 = 0001 , 0000 ∣ 0000 = 0000 0001 \mid 0001 = 0001, 0001 \mid 0000 = 0001, 0000 \mid 0000 = 0000 0001∣0001=0001,0001∣0000=0001,0000∣0000=0000 |
| ∧ \wedge ∧ | 异或 | 两个位相同为 0 0 0,相异为 1 1 1。 | 0001 ∧ 0001 = 0000 , 0001 ∧ 0000 = 1 , 0000 ∧ 0000 = 0 0001 \wedge 0001 = 0000, 0001 \wedge 0000 = 1, 0000 \wedge 0000 = 0 0001∧0001=0000,0001∧0000=1,0000∧0000=0 |
| ∼ \sim ∼ | 取反 | 0 0 0 变 1 1 1, 1 1 1 变 0 0 0。 | ∼ 0 = 1 , ∼ 1 = 0 \sim 0 = 1, \sim 1 = 0 ∼0=1,∼1=0 |
| ≪ \ll ≪ | 左移 | 各二进位全部左移若干位,高位丢弃,低位补 0 0 0。 | 0001 ≪ k = 0100 0001 \ll k = 0100 0001≪k=0100, k = 2 k = 2 k=2, k k k 是左移的位数,这里 k = 2 k = 2 k=2 |
| ≫ \gg ≫ | 右移 | 各二进位全部右移若干位,对无符号数,高位补 0 0 0,有符号数,右移补 1 1 1。 | 0100 ≫ k = 0001 0100 \gg k = 0001 0100≫k=0001, k = 2 k = 2 k=2, k k k 是右移的位数,这里 k = 2 k = 2 k=2 |
看完,你可能会觉得挺简单的,但位运算的难点并不在这,而在于其性质、高级操作和它的应用。
2 位运算的性质
2.1 运算符的优先级
优先级需要弄清楚,如果不太清楚可以加小括号确保是想要的运算顺序,这里只是相对优先级,即只是和一些常用的算术运算符做比较。
| 优先级 | 运算符 | 结合方向 |
|---|---|---|
| 1 | − - −(符号运算符), ∼ \sim ∼(取反运算符), + + ++ ++(自增), − − -- −−(自减) | 从右到左 |
| 2 | × \times ×(乘), ÷ \div ÷(除), % \% %(取余) | 从左到右 |
| 3 | + + +(加), − - −(减) | 从左到右 |
| 4 | ≪ \ll ≪(左移), ≫ \gg ≫(右移) | 从左到右 |
| 5 | > \gt >(大于), < \lt < (小于), ≥ \geq ≥ (大于等于), ≤ \leq ≤ (小于等于) | 从左到右 |
| 6 | = = == == (等于), ! = != !=(不等于) | 从左到右 |
| 7 | & \& &(按位与) | 从左到右 |
| 8 | ∧ \wedge ∧ (按位异或) | 从左到右 |
| 9 | ∣ \mid ∣ (按位或) | 从左到右 |
2.2 位运算符的运算律
| 公式名称 | 运算规则 |
|---|---|
| 交换律 | A & B = B & A A \& B = B \& A A&B=B&A, A ∧ B = B ∧ A A \wedge B = B \wedge A A∧B=B∧A |
| 结合律(注意结合律只能在同符号下进行) | ( A & B ) & C = A & ( B & C ) (A \& B) \& C = A \& (B \& C) (A&B)&C=A&(B&C) |
| 等幂律 | A & A = A A \& A = A A&A=A, A ∣ A = A A \mid A = A A∣A=A |
| 零律 | A & 0 = 0 A \& 0 = 0 A&0=0 |
| 互补律(注意,这不同于逻辑运算) | A & ∼ A = 0 A \& \sim A = 0 A&∼A=0, A ∣ ∼ A = − 1 A \mid \sim A = -1 A∣∼A=−1 |
| 同一律 | A ∣ 0 = A A \mid 0 = A A∣0=A, A ∧ 0 = A A \wedge 0 = A A∧0=A |
以上仅为已证明的运算律(可能存在遗漏),其余的博主均认为是不符合不成立的,注意:千万不要将逻辑运算的运算律或者其他的运算律与这混为一谈。
3 位运算高级操作
如下表,请读者认真阅读理解,在阅读的过程中可以对示例进行运算。
| 功能 | 示例 | 位运算 |
|---|---|---|
| 去掉最后一位 | 0100 → 0010 0100 \to 0010 0100→0010 | x ≫ 1 x \gg 1 x≫1 |
| 在最后加一个 0 0 0 | 0100 → 1000 0100 \to 1000 0100→1000 | x ≪ 1 x \ll 1 x≪1 |
| 在最后加一个 1 1 1 | 0100 → 1001 0100 \to 1001 0100→1001 | ( x ≪ 1 ) + 1 (x \ll 1) + 1 (x≪1)+1 |
| 将最后一位变为 1 1 1 | 0100 → 0101 0100 \to 0101 0100→0101 | x ∣ 1 x \mid 1 x∣1 |
| 将最后一位变为 0 0 0 | 0101 → 0100 0101 \to 0100 0101→0100,这里实际上就是先确保最低位变为 1 1 1,再减去 1 1 1。 | ( x ∣ 1 ) − 1 (x \mid 1) - 1 (x∣1)−1 |
| 最后一位取反 | 0100 → 0101 0100 \to 0101 0100→0101,利用异或性质,其中除最后一位其余不变。 | x ∧ 1 x \wedge 1 x∧1 |
| 把右数的第 k k k 位变为 1 1 1 | 0001 → 1001 , k = 4 0001 \to 1001, k = 4 0001→1001,k=4 | x ∣ ( 1 ≪ ( k − 1 ) ) x \mid (1 \ll (k - 1)) x∣(1≪(k−1)) |
| 把右数的第 k k k 位变为 0 0 0 | 1001 → 0001 , k = 4 1001 \to 0001, k = 4 1001→0001,k=4,这个操作实际上就是先得到了 1000 1000 1000,然后取反得到 0111 0111 0111,最后利用按位与的性质其余位不变,最高位为 0 0 0 | x & ( ∼ ( 1 ≪ ( k − 1 ) ) ) x \& (\sim(1 \ll (k - 1))) x&(∼(1≪(k−1))) |
| 把右数的第 k k k 位取反 | 1000 → 0000 , k = 4 1000 \to 0000, k = 4 1000→0000,k=4,利用异或性质 | x ∧ ( 1 ≪ ( k − 1 ) ) x \wedge (1 \ll (k - 1)) x∧(1≪(k−1)) |
| 取末 k k k 位 | 1011 → 0011 , k = 2 1011 \to 0011, k = 2 1011→0011,k=2 | x & ( ( 1 ≪ k ) − 1 ) x \& ((1 \ll k) - 1) x&((1≪k)−1) |
| 取右数的第 k k k 位 | 1011 → 0001 , k = 4 1011 \to 0001, k = 4 1011→0001,k=4,右移 k − 1 k - 1 k−1 位则是去掉了最后的 k − 1 k - 1 k−1 位,我们利用按位与即可将其提取出来 | x ≫ ( k − 1 ) & 1 x \gg (k - 1) \& 1 x≫(k−1)&1 |
| 把末 k k k 位全变为 1 1 1 | 1000 → 1111 , k = 3 1000 \to 1111, k = 3 1000→1111,k=3 | x ∣ ( ( 1 ≪ k ) − 1 ) x \mid ((1 \ll k) - 1) x∣((1≪k)−1) |
| 把末 k k k 位取反 | 0101 → 1010 , k = 4 0101 \to 1010, k = 4 0101→1010,k=4 | x ∧ ( ( 1 ≪ k ) − 1 ) x \wedge ((1 \ll k) - 1) x∧((1≪k)−1) |
| 把右边连续的 1 1 1 变为 0 0 0 | 0111 → 0000 0111 \to 0000 0111→0000,注意是右起连续的 1 1 1 | x & ( x + 1 ) x \& (x + 1) x&(x+1) |
| 把右起的第一个 0 0 0 变为 1 1 1 | 0011 → 0111 0011 \to 0111 0011→0111 | x ∣ ( x + 1 ) x \mid (x + 1) x∣(x+1) |
| 把右起连续的 0 0 0 变为 1 1 1 | 1000 → 1111 1000 \to 1111 1000→1111,注意是右起连续的 0 0 0 | x ∣ ( x − 1 ) x \mid (x - 1) x∣(x−1) |
| 取右边连续的 1 1 1 | 1011 → 0011 1011 \to 0011 1011→0011 | ( x ∧ ( x + 1 ) ) ≫ 1 (x \wedge (x + 1)) \gg 1 (x∧(x+1))≫1 |
| 去掉右起的第一个 1 1 1 的左边 | 1101 → 0001 1101 \to 0001 1101→0001 | x & ( x ∧ ( x − 1 ) ) x \& (x \wedge (x - 1)) x&(x∧(x−1)) |
当然,这里只是一些常用的,并不是全部,位运算的神奇远不止于此。
4 负数的位运算
首先,我们要知道,在计算机中,运算是使用的二进制补码,而正数的补码是它本身,负数的补码则是符号位不变,其余按位取反,最后再 + 1 + 1 +1 得到的, 例如:
15 15 15,原码: 00001111 00001111 00001111 补码: 00001111 00001111 00001111
− 15 - 15 −15,原码: 10001111 10001111 10001111 补码: 11110001 11110001 11110001
那么对于负数的位运算而言,它们的操作都是建立在补码上的,得到的运算结果是补码,最后将补码结果转化成一个普通的十进制数结果。
但需要注意的是,对于有符号数的右移操作,不同的处理器架构可能有不同的规定。在某些架构中(如x86),如果对有符号数执行算术右移(arithmetic right shift),则高位空出来的位置会补上符号位;对于无符号数的右移操作,所有架构都遵循相同的规则:高位空出来的位置会补
0
0
0。例如对于
−
15
- 15
−15,其补码为
11110001
11110001
11110001,右移一位
(
−
15
≫
1
)
(- 15 \gg 1)
(−15≫1) 得到的是
11111000
11111000
11111000,即
−
8
- 8
−8,其他的同理。
在大多数现代处理器上,无论是有符号数还是无符号数,左移操作总是将空出来的低位补
0
0
0。
这里我们介绍几个特殊的性质:
-
快速判断是否为 − 1 - 1 −1
在链式前向星中,我们初始化 h e a d head head 数组为 − 1 - 1 −1,最后判断是否遍历完 u u u 的所有边时,即判断 i i i 是否为 − 1 - 1 −1,我们直接用 ∼ i \sim i ∼i 即可。原因就在于 − 1 - 1 −1 的补码是 11111111 11111111 11111111,按位取反就变为 00000000 00000000 00000000,这实际上就是 0 0 0。
-
取最低位的 1 1 1,lowbit函数
也就是 x & ( − x ) x \& (- x) x&(−x),这在树状数组中起着巨大作用,这里指路一篇树状数组讲解:
- 树状数组详解(一维+二维+差分+前缀和+公式优化)_差分树状数组 - CSDN博客
https://blog.csdn.net/hzf0701/article/details/116208699
我们来证明一下,这里取 x = 15 x = 15 x=15,对于 15 & ( − 15 ) 15 \& (- 15) 15&(−15),我们知道,在补码上进行运算得到的是 00000001 00000001 00000001,需要注意二元运算的符号位我们需要进行运算。
- 树状数组详解(一维+二维+差分+前缀和+公式优化)_差分树状数组 - CSDN博客
5 位运算的一些应用
-
位运算实现乘除法
将 x x x 左移一位实现 × 2 \times 2 ×2,将 x x x 右移一位实现 ÷ 2 \div 2 ÷2。
a ≪ 1 ≡ a × 2 a \ll 1 \equiv a \times 2 a≪1≡a×2
a ≫ 1 ≡ a ÷ 2 a \gg 1 \equiv a \div 2 a≫1≡a÷2
-
位运算交换两整数
void swap(int &a,int &b){
a ^= b;
b ^= a;
a ^= b;
}
这效率非常高,我们来剖析其原理,对于 a = a ∧ b a = a \wedge b a=a∧b,则 b = b ∧ ( a ∧ b ) b = b \wedge (a \wedge b) b=b∧(a∧b),根据交换律以及异或性质,得 b = b ∧ b ∧ a = 0 ∧ a = a b = b \wedge b \wedge a = 0 \wedge a = a b=b∧b∧a=0∧a=a,同理 a = ( a ∧ b ) ∧ a = 0 ∧ b = b a = (a \wedge b) \wedge a = 0 \wedge b = b a=(a∧b)∧a=0∧b=b。这样就实现了交换操作。
-
位运算判断奇偶数
我们知道,在二进制中,最低位决定了是奇数还是偶数,所以我们可以提取出最低位的值,即与 1 1 1 相与即可实现目的,为 0 0 0 则是偶数,为 1 1 1 则是奇数。
-
位运算改变正负性和求绝对值
int change(int a){
return ~ a + 1;
}
对于正数而言,补码就是原码,所以按位取反再 + 1 + 1 +1 则得到对应真值负数的补码,而对于负数,其补码进行按位取反再 + 1 + 1 +1 则得到对应真值正数的补码,变为原码。那么知道这个我们就可以特判是否为负数 (这里通过右移 31 31 31 位,若为正数,则得到的是 0 0 0,若为负数,则得到的是 − 1 - 1 −1,而 0 0 0 的补码为 0000 0000 0000, − 1 - 1 −1 的补码为 1111 1111 1111,根据异或性质即可判断感谢读者(恢。)指出错误,这里应该是要进行按位取反操作,这样如果为负数判断结果才为 0 0 0 。) ,利用条件表达式就可以根据判断结果求绝对值了。如下:
int abs(int a){
return ~(a >> 31)? a : ~a + 1;
}
- 位运算实现对 p p p 取余( p p p 为 2 k 2^k 2k)
int mod(int a,int p){
return a & (p - 1);
}
取余实际上就是舍去大于等于 p p p 的位数,所以我们只需要保留在 p p p 范围内的数。由于我们限定了 p p p 为 2 k 2^k 2k,所以 ( p − 1 ) (p - 1) (p−1) 一定是将小于 p p p 的最高位全部变为了 1 1 1,这样再进行与操作即可得到余数。
- 位运算统计二进制数 1 1 1 的个数
int count(int x){
int cnt = 0;
while(x){
x = x & (x - 1);
cnt ++;
}
return cnt;
}
对于任意的
x
x
x,转换成二进制后,是形如这样的数字:
a
a
⋯
a
a
10
⋯
00
aa\cdots aa10\cdots 00
aa⋯aa10⋯00,从右向左数有任意多个
0
0
0,直到遇见第一个
1
1
1,字母
a
a
a 用来占位,代表
1
1
1 左边的任意数字。
x
−
1
x - 1
x−1 转换成二进制后,是形如这样的数字:
a
a
⋯
a
a
01
⋯
11
aa\cdots aa01\cdots 11
aa⋯aa01⋯11,从右向左数,原来的任意多个0 都变成
1
1
1,原来的第一个
1
1
1 变成
0
0
0,字母
a
a
a 部分不变。对
x
x
x 和
x
−
1
x - 1
x−1 进行按位与计算,会得到:
a
a
⋯
a
a
00
⋯
00
aa\cdots aa00\cdots 00
aa⋯aa00⋯00,从右向左数,原来的第一个
1
1
1 变成了
0
0
0,字母
a
a
a 部分不变。所以
x
&
(
x
−
1
)
x \& (x - 1)
x&(x−1) 相当于消除了
x
x
x 从右向左数遇到的第一个
1
1
1。那么,
x
x
x 转换成二进制后包含多少个
1
1
1, count 函数里的循环就会进行多少次,直到
x
x
x 所有的
1
1
1 都被“消除”。
6 位运算例题
6.1 更新二进制位
-
题面
给出两个 32 位的整数 N N N 和 M M M,以及两个二进制位的位置 i i i 和 j j j。写一个方法来使得 N N N 中的第 i i i 到 j j j 位等于 M M M( M M M 会是 N N N 中从第 i i i 位开始到第 j j j 位的子串)。
样例:
输入: $N=(10000000000)_2$ $M=(10101)_2$ $i = 2$ $j = 6$ 输出: $N=(10001010100)_2$ 输入: $N=(10000000000)_2$ $M=(11111)_2$ $i = 2$ $j = 6$ 输出: $N=(10001111100)_2$ -
解题思路
结合所学,我们的思路应该就是先将第 i i i 位到第 j j j 位全部变为 0 0 0,再将与左移 i i i 位的 M M M 进行或操作。
-
AC 代码
class Solution {
public:
int updateBits(int n, int m, int i, int j) {
// 循环遍历从第 i 位到第 j 位
for(int pos = i; pos <= j; pos ++ ){
// 将 n 的第 pos 位设为 0
// ~(1 << pos) 创建一个在第 pos 位为 0 其他位为 1 的掩码
// 然后使用按位与运算符(&)来将 n 的第 pos 位设置为 0
n &= ~(1 << pos);
}
// 将 m 左移 i 位,使 m 的低位对齐到 n 的第 i 位
// 然后使用按位或运算符(|)合并 n 和 m
// 这样 n 的第 i 到第 j 位就被 m 的相应位所替换
return n | (m << i);
}
};
6.2 A + B 问题
-
题面
给出两个整数 a a a 和 b b b,求它们的和并以整数(
int)的形式返回。不能使用 + 等数学运算符。样例:
输入:
a = 1 b = 2输出:
3输入:
a = -1 b = 1输出:
0 -
解题思路
这题我们可以利用异或操作来实现,因为异或操作有一个别名叫不进位加法。那么进位操作我们实际上就可以通过 a & b a \& b a&b 来实现,因为 a & b a \& b a&b 得到的都是 a a a 和 b b b 上都有的 1 1 1,我们再左移即得到的是进位之后的结果,所以 a + b = ( a ∧ b ) + ( a & b ≪ 1 ) a + b=(a \wedge b)+(a \& b \ll 1) a+b=(a∧b)+(a&b≪1)。通过这样模拟竖式加法操作即可。
-
AC 代码
class Solution {
public:
int aplusb(int a, int b) {
// 当没有进位需要处理时循环结束
while(b != 0){
// temp_a 存储 a 和 b 的按位异或结果,这相当于不带进位的加法
int temp_a = a ^ b;
// temp_b 存储 a 和 b 的按位与结果并左移一位,这相当于计算进位
// 因为只有两个位都是 1 时才会产生进位
int temp_b = (a & b) << 1;
// 更新 a 为不带进位的加法结果
a = temp_a;
// 更新 b 为进位
b = temp_b;
}
// 当没有进位时,a 中存储了最终结果,返回 a
return a;
}
};
6.3 O(1) 时间检测 2 的幂次
-
题面
用 O( 1 1 1) 时间检测整数 n n n 是否是 2 2 2 的幂次。
样例
n = 4,返回true;n = 5,返回false。挑战
O( 1 1 1) 时间复杂度
-
解题思路
首先我们知道 2 k 2^k 2k 是大于 0 0 0 的,这里我们需要特判,同理, 2 k 2^k 2k 的二进制表示中只有 1 1 1 个 1 1 1,故我们可以利用 x & ( x − 1 ) x \& (x - 1) x&(x−1) 来消除唯一的 1 1 1 判断是否等于 0 0 0 即可。
-
AC 代码
class Solution {
public:
bool checkPowerOf2(int n) {
// 检查 n 是否大于 0
// 2 的幂必须是正数,因为 0 和负数都不是 2 的幂
// 检查 n 和 n - 1 的按位与操作是否为 0
// 如果 n 是 2 的幂,则其二进制表示中只有一个 1
// 例如 2 (10), 4 (100), 8 (1000)
// 当 n 是 2 的幂时,n - 1 的二进制表示是 n 的最高位 1 变为 0,
// 其余位从 0 变为 1,例如 2 (10) - 1 = 1 (01), 4 (100) - 1 = 3 (011)
// 因此 n & (n - 1) 将得到 0
return n > 0 && (n & (n - 1)) == 0;
}
};
& 与 && 的区别
一个不务正业的程序猿 2017-07-24 10:27:11
一、&与&&的区别
-
按位与:
a&b是将a和b都转换为二进制数,然后进行与运算。 -
逻辑与:
a&&b仅当两个操作数均为true时,结果才为true;只要有一个为false,a&&b即为false。&&进行短路判断,若左侧表达式结果为false,整个结果即为false,不再计算右侧表达式的值。示例代码(C++):
int main() {
int a = 0, b = 1;
a && b ++; //a为0,即左侧的表示的结果为false,整个的结果就为false,不再计算右侧的表达式
cout<<b;
return 0;
}
输出结果:
1
Process returned 0 (0x0) execution time : 0.045 s
Press any key to continue.
二、|| 与 | 的区别
&&和||是短路运算符,&和|是非短路运算符。- &&与&的区别:两者均表示“与”运算,但
&&运算符在第一个表达式不成立时,后面的表达式不运算,直接返回;而&对所有表达式都要进行判断。 - ||与|的区别:两者均表示“或”运算,但
||运算符在第一个表达式成立时,后面的表达式不运算,直接返回;而|对所有表达式都要进行判断。
逻辑运算符 && 和 & 的区别、| 和 || 的区别
汐小旅Shiory 2019-04-13 15:23:50
1. &和&&的区别
相同点
最终得到的boolean值结果一致,均为“并且and”的意思。
不同点
&既是逻辑运算符也是位运算符;&&仅是逻辑运算符。&不具备短路效果,即左边为false时,右边仍会执行;&&具有短路效果,左边为false时,右边则不执行。
2. | 和 || 的区别
相同点
最终得到的boolean值结果一致,均为“或者or”的意思。
不同点
|既是逻辑运算符也是位运算符;||仅是逻辑运算符。|不具备短路效果,即左边为true时,右边仍会执行;||具有短路效果,左边为true时,右边则不执行。
3. 结论
开发中常用&&和||进行逻辑运算,因其具有短路效果,可提升程序运行效率,优化程序。
& 和 && 的区别(简单易懂)
大雄有哆啦梦 2022-01-26 12:16:01
&(按位与)和 &&(逻辑与)的区别如下
&&具有短路功能,而&不具有短路功能。- 当
&运算符两侧的表达式结果均为真时,整个运算结果才为真。当&&操作符第一个表达式为false时,结果为false,并且不再计算第二个表达式。- 简单表述:使用
&运算符,必须两侧均为true,结果才为真。使用&&运算符,重点看第一个表达式,若第一个表达式为false,后面的表达式不再计算(因其具有短路功能);若第一个表达式为true,则继续计算后面的表达式,直至后面全部为true,结果才为真。 - 示例代码(Java):
引入变量命名规范:变量名字可大小写混用,但首字符应小写。词由大写字母分隔,限制用下划线,限制使用美元符($),因为该字符对内部类有特殊含义。示例:resultOne。
- 简单表述:使用
boolean resultOne = 1==3 & 1==1 & 2==2; //使用 &
boolean resultTwo = 1==3 && 1==1 && 2==2; //使用 &&
System.out.println(resultOne); //resultOne = false
System.out.println(resultTwo); //resultTwo = false
//当使用 & 时,要进行 1==3 & 1==1 & 2==2 的判断
//当使用 && 时,因为 1==3 为 false,所以进行了短路的操作,后面的1==1 && 2==2 不用执行。
在很多情况下会使用&&而不用&,例如在验证用户登录时进行判断,用户名不为空(null)也不是空字符串,代码应写成:
userName != null && !userName.equals("");
//这里不能使用 & 运算符,顺序也不能交换,如果用户名真的为空的情况下,会报空指针异常(NullPointerException)。
userName.equals("")若userName为null进行equals操作会报NullPointerException,因此要先判断userName不为null,再用equals判断不是空字符串。
运算符“||”与“|”,“&&”和“&”的区别(附带各类位运算符号详解(&、|、^、~、<<、>>、>>>)
Koikoi123 2022-10-20 10:15:22
区别一:定义不同
||和|均表示“或”,区别在于||只要满足第一个条件,后面的条件就不再判断,而|要对所有条件进行判断。
区别二:与操作和或操作的区别
- 在Java程序中,使用与操作,要求所有表达式的判断结果均为
TRUE,才为真;若有一个为FALSE,则最终判断结果为FALSE。 - 使用或操作,只要其中有一个表达式为
TRUE,则最终结果为TRUE;只有当所有表达式为FALSE时,最终结果才为FALSE。
区别三:实际含义不同
||:若左边计算后的操作数为true,右边则不再执行,返回true。|:前后两个操作数都会进行计算,即|不存在短路。
区别四:举例说明
- 使用
|时:若前面的表达式为真,程序会继续执行后面的表达式,然后得出TRUE的结果。
- 示例代码(Java):
public class Test{
public static void main(String[] args){
int i = 0;
if(10==10 | (i++)!=0){
System.out.printIn("结果为真 "+i);
}
}
}
- 结果:结果为真 1
- 使用
||(短路或)时:若前面的表达式结果为真,则程序不会再执行后面的表达式,直接得出TRUE的结果。- 示例代码(Java):
public class Test{
public static void main(String[] args){
int i = 0;
if(10==10 || (i++)!=0){
System.out.printIn("结果为真 "+i);
}
}
}
- 结果:结果为假 0
同理,&&是逻辑与(短路与),当第一个判断条件不满足要求时(返回false),第二个判断条件就不会执行;只有当两个判断条件都返回true时,整个逻辑运算才返回true。&按位与,不论何种情况,两边的判断条件都会执行,当两边都返回true时,按位与才返回true。
Java 中的位运算符号详解(&、|、^、~、<<、>>、>>>)
羽觞醉月11 2022-06-11 01:51:15
1. 位运算符号概览
| 符号 | 描述 | 运算规则 |
|---|---|---|
| & | 与 | 两个位都为 1 时,结果才为 1 |
| | | 或 | 两个位都为 0 时,结果才为 0 |
| ^ | 异或 | 两个位相同为 0,不同为 1 |
| ~ | 取反 | 所有位置 0 变 1,1 变 0 |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补 0 |
| >> | 带符号右移 | 各二进位全部右移若干位,低位丢弃,高位补为符号位 |
| >>> | 无符号右移 | 各二进位全部右移若干位,低位丢弃,高位补 0 |
还有两个符号,并非位运算符,但易与位运算符混淆,后续将其与相似的位运算符一并讲解:
| 符号 | 描述 | 运算规则 |
|---|---|---|
| && | 逻辑与 | 左右表达式均为 true 时,运算最终结果才为 true |
| || | 逻辑非 | 左右表达式只要有一个为 true,运算最终结果就为 true |
2. 一个工具
以下函数可用于打印Java中int整型在底层的32位信息,便于后续调试程序:
public static void print(int num) {
for (int i = 31; i >= 0; i--) {
System.out.print((num & (1 << i)) == 0? "0" : "1");
}
System.out.println();
}
// print(1); --> 00000000000000000000000000000001
// print(-1); --> 11111111111111111111111111111111
// print(Integer.MAX_VALUE); --> 01111111111111111111111111111111
// print(Integer.MAX_VALUE); --> 10000000000000000000000000000000
下面开始对每个符号进行介绍。
3. 按位与(&)、逻辑与(&&)
按位与(&)
具体运算规则为:
1 & 1 = 1 1 & 0 = 0 0 & 1 = 0 0 & 0 = 0
举例:
print(123); // 00000000000000000000000001111011
print(321); // 00000000000000000000000101000001
print(a & b); // 00000000000000000000000001000001
// 任何数与0相与都等于0
// 任何数与自己相与都等于自己
在Java中,&不仅可作为位运算符号,也可作为逻辑与符号。需注意:&&并非位运算符号,不可参与位运算!
逻辑与(&)、逻辑与(&&)
具体运算规则为:
true & true = true true & false = false
false & true = false false & false = false
true && true = true true && false = false
false && true = false false && false = false
两者区别在于:逻辑与(&)在运算时,不论&前面的表达式结果是否为false,&后面的表达式都会执行运算;而逻辑与(&&)在运算时,若&&前面的表达式结果为false,则&&后面的表达式不会执行运算。
4. 按位或(|)、逻辑或(||)
按位与(|)
具体运算规则为:
1 | 1 = 1 1 | 0 = 1 0 | 1 = 1 0 | 0 = 0
- 举例:
print(123); // 00000000000000000000000001111011
print(321); // 00000000000000000000000101000001
print(a | b); // 00000000000000000000000101111011
// 任何数与0相或都等于自身
// 任何数与自己相或都等于自己
在Java中,|不仅可作为位运算符号,也可作为逻辑与符号。需注意:||并非位运算符号,不可参与位运算!
逻辑或(|)、逻辑或(||)
具体运算规则为:
true | true = true true | false = true
false | true = true false | false = false
true || true = true true || false = true
false || true = true false || false = false
两者区别在于:逻辑或(|)在运算时,不论|前面的表达式结果是否为true,|后面的表达式都会执行运算;而逻辑或(||)在运算时,若||前面的表达式结果为true,则||后面的表达式不会执行运算。
5. 异或(^)
具体运算规则为:
1 ^ 1 = 0 1 ^ 0 = 1 0 ^ 1 = 1 0 ^ 0 = 0
// 即相同为0,不同为1
- 举例:
print(123); // 00000000000000000000000001111011
print(321); // 00000000000000000000000101000001
print(a ^ b); // 00000000000000000000000100111010
// 任何数与0异或都等于自身
// 任何数与自己异或都为0
6. 取反(~)
具体运算规则为:
~1 = 0 ~0 = 1
- 举例:
print(123); // 00000000000000000000000001111011
print(~a); // 11111111111111111111111110000100
// 符号位也取反
取反(~)可用于求相反数:
// 一个32整数,取反再+1,就是该数的相反数,效果等同于加负号(-)
int a = 123;
System.out.println(a); // 123
System.out.println(~a+1); // -123
说明:由于Java中int类型的整数范围为
−
2
31
∼
2
31
−
1
-2^{31}\sim2^{31}-1
−231∼231−1,负数的个数比正数多一个,导致所有正数都有相应的负的相反数,但并非所有负数都有正的相反数:
a = Integer.MIN_VALUE;
System.out.println(a); // -2147483648
print(a); // 10000000000000000000000000000000
System.out.println(~a+1); // -2147483648
print(~a + 1); // 100000000000000000000000000
// Java 中 int 整数最小值的相反数还是其自身
// 如果一定需要对 int 整数最小值求相反数,请将 int 类型换为long 类型
7. 左移(<<)
左移表示某数的各二进位全部左移若干位,高位丢弃,低位补0。
// 举例:
print(123); // 00000000000000000000000001111011
print(123 << 1); // 00000000000000000000000011110110
// 整体左移1位,高位丢弃,低位补0
应用:
// 左移 1 位相当于在原数的基础上乘以 2
System.out.println(123); // 123
System.out.println(123<<1); // 246
// 左移2位相当于在原数的基础上乘以4
System.out.println(2); // 2
System.out.println(2<<2); // 8
// 左移3位、4位...以此类推
8. 带符号右移(>>)、无符号右移(>>>)
带符号右移(>>)
指各二进位全部右移若干位,低位丢弃,高位补为符号位。
无符号右移(>>>)
指各二进位全部右移若干位,低位丢弃,高位补0。
int a = 123;
print(a); // 00000000000000000000000001111011
print(a>>2); // 00000000000000000000000000011110
print(a>>>2); // 00000000000000000000000000011110
int b = -123;
print(b); // 11111111111111111111111110000101
print(b>>2); // 11111111111111111111111111100001
print(b>>>2); // 00111111111111111111111111100001
// 区别就在于:一个高位用符号位补,一个高位用 0 补
9. Java 中没有(<<<)符号!
C 语言逻辑运算符:&& 和 ||
南雨兮 2023-01-02 14:23:27
1. 简单介绍 && 和 ||
&&和||是逻辑运算符,分别为逻辑与(&&)和逻辑或(||)。
逻辑与(&&)
存在三种情况:
- 当逻辑与左边为
false(假),则不再进行逻辑与右边的判断,结果为false(假)。 - 当逻辑与左边为
true(真),则进行右边判断,若右边为false(假),结果为false(假)。 - 当逻辑与左边为
true(真),则进行右边判断,若右边也为true(真),则结果为true(真)。
逻辑或(||)
存在三种情况:
- 当逻辑或左边为
false(假),继续逻辑或右边的判断,若右边也为false(假),结果为false(假)。 - 当逻辑或左边为
false(假),继续逻辑或右边的判断,若右边为true(真),结果为true(真)。 - 当逻辑或左边为
true(真),则不再进行逻辑或右边的判断,结果为true(真)。
2. && 和 || 的使用
逻辑与(&&)
通过以下程序进行讲解:
#include <stdio.h>
#include <string.h> // strcmp所在头文件
int main(void)
{
char szAccount[] = "account"; // 设置的默认账号
char szPassword[] = "password"; // 设置的默认密码
char szInputAccount[32] = { 0 }; // 输入的账号
char szInputPassword[32] = { 0 }; // 输入的密码
// 获取输入的账号
printf("请输入账号: ");
scanf_s("%s", szInputAccount, 32);
// 获取输入的密码
printf("请输入密码: ");
scanf_s("%s", szInputPassword, 32);
// 通过strcmp函数进行比较输入的账号和密码是否跟我们设置的匹配
// 通过 &&(逻辑与) 进行判断,当账号和密码都正确才会打印出 "账号密码正确!"
if (strcmp(szInputAccount, szAccount) == 0 &&
strcmp(szInputPassword, szPassword) == 0) {
printf("账号密码正确!");
}
else {
printf("账号或密码错误!");
}
return 0;
}
程序简介:
定义了一个char(字符型)的数组变量szAccount,并初始化为"account";
定义了一个char(字符型)的数组变量szPassword,并初始化为"password";
定义了一个char(字符型)的数组变量szInputAccount,并将数组中的每个元素都初始化为0;
定义了一个char(字符型)的数组变量szInputPassword,并将数组中的每个元素都初始化为0。
使用printf打印提示信息,提示用户输入账号,通过scanf_s获取用户输入的数据并保存到对应的变量szInputAccount中;
再次使用printf提示用户输入密码,通过scanf_s获取用户输入的数据并保存到对应的变量szInputPassword中。
strcmp函数用于比较两个传入的字符串,若两个字符串相同则返回0 。
通过&&(逻辑与)比较输入的账号和密码与默认设置的账号和密码,若都相同则打印"账号密码正确!",若有一个不正确则打印"账号或密码错误!"。
逻辑或(||)
#include <stdio.h>
int main(void)
{
char c;
char c1;
do {
/**
* 进行输入账号和密码的操作和判断
**/
// 此处只是为了清空输入缓冲区
while ((c1 = getchar()) != EOF && c1 != '\n') {}
// 密码错误进行是否继续输入进行匹配
printf("是否继续匹配,继续匹配请输入(y或者Y)\n");
c = getchar();
} while ('y' == c || 'Y' == c);
return 0;
}
程序讲解:
定义了一个char(字符型)变量c和一个char(字符型)变量c1。使用do...while循环不断进行账号密码的判断操作。while循环用于清空输入缓冲区,因为不清空输入缓冲区的内容,下面的getchar会获取不确定的内容。最后通过||(逻辑或)判断是否继续输入,若输入的是'y'或者'Y',则继续进行循环输入匹配。
C语言中的 |、||、&、&&、^、~、<<、>>运算符
凉云生烟 2023-04-01 22:54:10
位运算
现代计算机中所有数据以二进制形式存储在设备中,即 0、1 两种状态。计算机对二进制数据进行的运算(+、-、*、/)都称为位运算,即将符号位共同参与运算的运算。位运算是把运算对象看作由二进位组成的位串信息,按位完成指定运算,得到位串信息的结果。位运算的运算分量只能是整型或字符型数据。
例如,计算两个数的和:
int a = 25 ;
int b = 43 ;
int c = a + b ;
在计算机中,int变量会先转换为二进制再相加:
25: 0 0 0 1 1 0 0 1
43: 0 0 1 0 1 0 1 1
-------------------
68: 0 1 0 0 0 1 0 0
相比直接使用(+、-、*、/)运算符,合理运用位运算能显著提高代码在机器上的执行效率。
位运算符
位运算符用于处理数据的位运算 。在相关运算符中,位运算符有:&(按位与)、|(按位或)、^(按位异或)、~ (按位取反)。其中,只有~ (按位取反)运算符是单目运算符,其余均为双目运算符。
优先级
位运算符的优先级从高到低依次为:~、<<、>>、&(按位与)、^、| 。其中~的结合方向自右至左,且优先级高于算术运算符,其余运算符的结合方向都是自左至右,且优先级低于关系运算符。
按位与运算符(&)
定义为参加运算的两个数据,按二进制位进行“与”运算。按位与运算将两个运算分量的对应位按以下规则计算:
0&0=0 0&1=0 1&0=0 1&1=1
当两边同时为 1 时,结果才为 1,否则结果为 0,即全真为真,一假则假。注意,这里是按二进制位进行运算,如 3&5,即 0000 0011& 0000 0101 = 0000 0001,因此 3&5 的值为 1。负数将按补码形式参加按位与运算。
** 与运算的典型用法 **:
- 取一个数的指定位:比如取数
X = 1010 1110的低 4 位,只需另找一个数Y,令Y的低 4 位为 1,其余位为 0,即Y = 0000 1111,然后将X与Y进行按位与运算(X&Y = 0000 1110)即可得到X的指定位。 - 判断奇偶:在二进制中,可根据最末位是 0 还是 1 判断奇偶,为 0 则是偶数,为 1 则是奇数。所以可用
if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是否为偶数。 - 清零:若想将一个单元清零,使其全部二进制位为 0 即可,这时只要与一个各位都为零的数值相与,结果为零。
按位或运算符(|)
定义为参加运算的两个对象,按二进制位进行“或”运算。按位或运算将两个运算分量的对应位按以下规则计算:
0|0=0 0|1=1 1|0=1 1|1=1
参加运算的两个对象只要有一个为 1,其值为 1;全为 0 时,其值为 0,即一真全真,全假才假。注意,这里是按二进制位进行运算,如 3|5 即 0000 0011| 0000 0101 = 0000 0111,因此,3|5 的值为 7。负数按补码形式参加按位或运算。
** 或运算的典型用法 **:或运算通常用来对一个数据的某些位设置为 1,如将要将数 X = 1010 1110 的低 4 位设置为 1,只需另找一个数 Y,令 Y 的低 4 位为 1,其余位为 0,即 Y = 0000 1111,然后进行按位或运算(X|Y = 1010 1111)即可得到。
按位异或运算符(^)
定义为参加运算的两个数据,按二进制位进行“异或”运算。按位异或运算将两个运算分量的对应位按以下规则计算:
0^0=0 0^1=1 1^0=1 1^1=0
参加运算的两个对象对应位相同,其值为 0;否则其值为 1,即相应位的值相同为 0,不相同为 1。注意,这里是按二进制位进行运算,如 3^5 即 0000 0011^0000 0101 = 0000 0110,因此,3^5 的值为 6。
** 按位异或运算满足以下性质 **:
- 交换律:
a^b = b^a。 - 结合律:
(a^b)^c == a^(b^c)。 - 自反性:
a^b^b = a^0 = a。 - 自身与 0 性:任意一个数
N,都有N^0 = N;N^N = 0。
按位异或运算的典型用法:
-
翻转指定位:比如若要将数
X = 1010 1110的低 4 位进行翻转,只需另找一个数Y,令Y的低 4 位为 1,其余位为 0,即Y = 0000 1111,然后将X与Y进行异或运算(X^Y = 1010 0001)即可得到。 -
交换两个数:
void my_Swap(int &a, int &b)
{
if (a != b)
{
a ^= b ; //在这里 a^-b 等价于 a = a^b
b ^= a ;
a ^= b ;
}
}
举例:
如果a = 3, b = 5 ;
a 的二进制表达: 0000 0011
b 的二进制表达: 0000 0101
a^b = 0000 0110
a = 0000 0110
b^a = 0000 0011
b = 0000 0011
a^b = 0000 0101
a = 0000 0101
这样就完成了反转
按位取反运算符(~)
定义为参加运算的一个数据,按二进制进行“取反”运算。按位取反算将两个运算分量的对应位按以下规则计算:
~1=0 ~0=1
注意,按位取反运算是单目运算,用来求一个位串信息按位的反,即 0 变为 1,1 变为 0 。
按位取反运算的典型用法:可以使一个数的最低位为零。如果想要使 a 的最低位为 0,可以表示为:a & ~1。~1 的值为 1111 1111 1111 1110,再按 “与” 运算,最低位一定为 0。
左移运算符(<<)
定义为将一个运算对象的各二进制位全部左移若干位(最左边的二进制位丢弃,右边补 0)。例如 a = 1010 1110,a = a<< 2 将 a 的二进制位左移 2 位,左移时,空出的右端用 0 补充,左端移出的位的信息被丢弃,即得 a = 1011 1000。在二进制数运算中,在信息没有因移动而丢失的情况下,每左移 1 位相当于乘 2。例如 14<<1,结果为 0001 1100,也就是 14*2 = 28 。
右移运算符(>>)
定义为将一个数的各二进制位全部右移若干位,正数左补 0,负数左补 1,右边丢弃。例如:a = a>>2 将 a` 的二进制位右移 2 位,左补 0 或者左补 1 取决于被移数是正还是负,右端移出的位的信息被丢弃。
在右移时,需要注意符号位问题。对无符号数据,右移时,左端空出的位用 0 补充。对于带符号的数据,如果移位前符号位为 0(正数),则左端也是用 0 补充;如果移位前符号位为 1(负数),则左端用 0 或用 1 补充,取决于计算机系统。对于负数右移,称用 0 补充的系统为“逻辑右移”,用 1 补充的系统为“算术右移”。
操作数每右移一位,相当于该数除以 2,即 x > > n = x / ( 2 n ) x>>n = x/(2^n) x>>n=x/(2n) 。
总结
我们在此列出一张表来总结上面所学习的位运算符:
| 运算符 | 名称 | 运算规则 | 示例 |
|---|---|---|---|
| & | 按位与 | 两个位都为 1 时,结果才为 1 | (3 & 5 = 1) |
| | | 按位或 | 两个位都为 0 时,结果才为 0 | (3 | 5 = 7) |
| ^ | 按位异或 | 两个位相同为 0,不同为 1 | (3 ^ 5 = 6) |
| ~ | 按位取反 | 0 变 1,1 变 0 | (\sim 3 = -4) |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补 0 | (3 << 1 = 6) |
| >> | 带符号右移 | 各二进位全部右移若干位,低位丢弃,高位补为符号位 | (3 >> 1 = 1) |
| >>> | 无符号右移 | 各二进位全部右移若干位,低位丢弃,高位补 0 | (仅适用于 Java 等语言) |
逻辑运算符
逻辑运算符可以将两个或多个关系表达式连接成一个或使表达式的逻辑反转。C 语言支持的所有关系逻辑运算符有三个,分别是:&&(逻辑与运算符)、||(逻辑或运算符)、!(逻辑非运算符)。
优先级
&&、|| 和! 的优先级为:! > && > ||
当然,虽然运算符有着优先级的设定,但是在平时编写的时候,还是会建议使用括号去表明先后顺序,这样也更容易避免一些错误。
逻辑与运算符(&&)
&& 运算符被称为逻辑与运算符。它需要两个表达式作为操作数,并创建一个表达式,只有当两个子表达式都为 true 时,该表达式才为 true,也就是两边同真为真,一假则假。
举例:
if ((n < 20) && (m > 12))
{
printf("此时 n < 20 且 m > 12");
}
上述例子中,n 小于 20 时左侧为真,m > 12 时右侧为真,所以只有左右两侧均满足条件时,才会执行 if 语句,否则将不会执行。
逻辑或运算符(||)
|| 运算符被称为逻辑或运算符。它需要两个表达式作为操作数,并创建一个表达式,当任何一个子表达式为 true 时,该表达式为 true,也就是两边同假为假,一真则真。
举例:
if ((n < 20) || (m > 12))
{
printf("此时 n < 20 或 m > 12");
}
上述例子中,n 小于 20 时左侧为真,m > 12 时右侧为真,这时只有左右两侧同时不满足为真的条件时,才不会执行这个语句;否则,不论哪个为真,都要执行 if 语句。
逻辑非运算符(!)
! 运算符被称为逻辑非运算符,执行逻辑 NOT 操作。它可以反转一个操作数的真值或假值。换句话说,如果表达式为 true,那么! 运算符将返回 false,如果表达式为 false,则返回 true,也就是非真即假,非假即真。
举例:
if (!(n < 20))
{
printf("此时 n >= 20");
}
上述例子中,如果不加 “!” 号,则当 n < 20 的时候才可以执行 if 语句,但是如果运用逻辑非运算符后,就变成了,当 n >= 20 时才会执行该语句,条件就反了过来。
总结
| 运算符 | 术语 | 示例 | 结果 |
|---|---|---|---|
| ! | 非 | !a | 如果 a 为假,则 !a 为真; 如果 a 为真,则 !a 为假。 |
| && | 与 | a && b | 如果 a 和 b 都为真,则结果为真,否则为假。 |
| || | 或 | a || b | 如果 a 和 b 有一个为真,则结果为真; 二者都为假时,结果为假。 |
via
-
Understanding Bitwise Operations and Their Uses in Programming_.
https://algocademy.com/blog/understanding-bitwise-operations-and-their-uses-in-programming/ -
operators - What are the advantages of using bitwise operations? - Software Engineering Stack Exchange
https://softwareengineering.stackexchange.com/questions/13798/what-are-the-advantages-of-using-bitwise-operations -
computer architecture - Why is addition as fast as bit-wise operations in modern processors? - Computer Science Stack Exchange
https://cs.stackexchange.com/questions/75811/why-is-addition-as-fast-as-bit-wise-operations-in-modern-processors -
位运算全面总结,关于位运算看这篇就够了-CSDN博客_.(讨论见原文)
https://blog.csdn.net/hzf0701/article/details/117359478
— -
& 与 && 的区别 - CSDN 博客
https://blog.csdn.net/cloud323/article/details/75981709 -
逻辑运算符 && 和 & 的区别、| 和 || 的区别 - CSDN 博客
https://blog.csdn.net/zhuzbYR/article/details/89283067 -
& 和 && 的区别(简单易懂) - CSDN 博客
https://blog.csdn.net/weixin_46015018/article/details/122523030 -
运算符“||”与“|”,“&&”和“&”的区别 (附带各类位运算符号详解(&、|、^、~、<<、>>、>>>) - CSDN 博客
https://blog.csdn.net/Koikoi12/article/details/120062014 -
Java 中的位运算符号详解(&、|、^、~、<<、>>、>>>)_java & 符号 - CSDN 博客
https://blog.csdn.net/qq_44494578/article/details/125230581 -
C 语言逻辑运算符: && 和 ||_c 语言中 && 和 || 的用法 - CSDN 博客
https://blog.csdn.net/qq_31243065/article/details/82659669_ -
C 语言中的 |、||、&、&&、^、~、<<、>> 运算符_c 语言 | - CSDN 博客
https://blog.csdn.net/qq_62464995/article/details/126579302
