工程经济对折现率选择的理论、方法与行业实践研究

1.折现率的理论基础与概念内涵

折现率在工程经济学（或称：技术经济）中居于核心地位，它是连接未来收益与当前价值的桥梁。在投资决策、项目评估和资产估值中，折现率是将未来不同时期的现金流量折算为现值的关键参数。
从经济本质来看，​折现率反映了资金的时间价值和风险补偿。其中，资金的时间价值体现了货币随时间的自然增值能力，而风险补偿则是对投资者承担不确定性所需的额外回报。在工程经济评估中，折现率的选择直接影响着项目可行性判断、方案比选和资源配置效率。

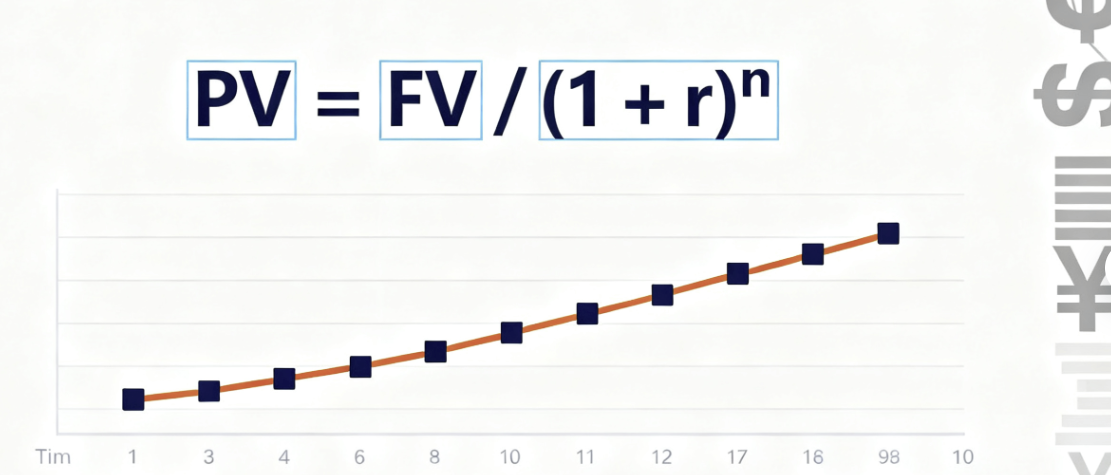
折现率的数学表达为现值计算中的分母部分，其基本公式为：PV = FV / (1 + r)^t，其中PV为现值，FV为未来值，r为折现率，t为时间期数。这一简单公式背后蕴含着深刻的经济学原理——即当前拥有的资金比未来同样金额的资金更有价值，这种价值差异通过折现率得以量化。在工程项目的全生命周期成本效益分析中，​折现率决定了项目经济性评价的准确性和可靠性。

从投资者视角看，折现率代表了机会成本的概念，即投资者因选择当前项目而放弃的其他最佳投资机会所能获得的收益率。因此，折现率的最低限度不应低于无风险投资收益率，通常以国债利率或银行存款利率作为基准。在实际应用中，折现率还需要考虑通货膨胀、流动性限制、市场风险和政策变化等多种因素，形成一个综合反映投资环境复杂性的参数体系。

折现率的理论发展经历了从简单到复杂、从单一到多元的演变过程。早期工程经济评估多采用单一固定折现率，现代评估方法则倾向于根据项目特性和风险特征调整折现率，甚至采用随时间变化的动态折现率模型。这种演变反映了人们对投资决策复杂性认识的深化，以及对风险评估精确化要求的提高。

2.折现率的主要确定方法与理论模型

2.1.资本资产定价模型（CAPM）

资本资产定价模型（CAPM）是确定折现率中最广泛应用的理论模型之一。CAPM建立了系统风险与预期收益之间的关系，其基本公式为：Re = Rf + β × (Rm - Rf) + ε。其中，Re为股权期望报酬率，Rf为无风险利率，β是衡量资产相对于市场波动性的贝塔系数，(Rm - Rf)表示市场风险溢价，ε是对企业特定风险的调整值。

• 无风险利率Rf通常基于长期国债收益率确定，提供基本回报基准。在中国债券信息网发布的10年期中债国债收益率常被作为无风险利率的参考，如2022年这一数值为2.845%。
• 市场风险溢价(Rm-Rf) 反映投资者承担市场风险的额外期望收益，采用沪深300指数作为基准时，通过回归分析方法计算的市场风险溢价可能达到5.86%。
• 贝塔系数β衡量投资相对于市场的风险水平，特定风险调整系数则补偿企业特有风险，如经营阶段、财务风险、业务地区分布、管理团队经验和内部控制机制等因素。

表：CAPM模型主要参数及确定方法

参数​	含义 ​	​确定方法 ​	​示例值​
无风险利率(Rf)​​	无违约风险投资收益率	长期国债收益率	2.845%
市场风险溢价(Rm-Rf)​​	市场收益超过无风险利率的部分	历史市场数据回归分析	5.86%
贝塔系数(β)​​	资产相对于市场波动性的测量	可比上市公司数据分析	0.6891
​特定风险调整(ε)​​	企业特有风险补偿	综合评估企业特定风险	2.00%

2.2.加权平均资本成本（WACC）

加权平均资本成本（WACC） 是另一种重要的折现率确定方法，它考虑了企业资本结构中债务和股权的比例关系。WACC的计算公式为：WACC = Re × E/(D+E) + Rd × D/(D+E) × (1－T)。其中，Re代表股权期望报酬率，Rd是债权期望报酬率，E和D分别代表股权和债务的市场价值，T是所得税税率。

WACC的优势在于反映了企业整体资本成本，而不仅仅是股权成本。

• 债权期望报酬率通常基于企业实际债务成本或市场中长期贷款利率确定，如4.65