当前位置： 首页 > news >正文

牛客算法_模拟

news 2025/10/13 8:12:25

1、旋转数组

描述

一个数组A中存有 n 个整数，在不允许使用另外数组的前提下，将每个整数循环向右移 M（ M >=0）个位置，即将A中的数据由（A0 A1 ……AN-1 ）变换为（AN-M …… AN-1 A0 A1 ……AN-M-1 ）（最后 M 个数循环移至最前面的 M 个位置）。如果需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

数据范围：0<n≤1000<n≤100，0≤m≤10000≤m≤1000

进阶：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n)

思路：

1. m >=n 时，是循环移动， 计算出最少移动位数 m % n

2. 用index记录移动m位后的下标。a[0] 移动m位置到a[m]后， 用pre表示前一个值， 并将pre赋值给当前位置， 当前位置的旧值记成pre。 继续判断a[m]移动后的结果。

3. n=偶数时， 遍历完一遍数组后会又到达a[0]位置，这是手动将下标 i+1, 同时pre=a[1],  即从奇数位重新赋值。

4. n=奇数时， 不用考虑这个问题， 会自动全部遍历完。

 public int[] solve(int n, int m, int[] a) {int bit = m < n ? m : (m % n);if (bit == 0) {return a;}Boolean first = false;Boolean second = false;int i = 0;int pre = a[0];while (!(first == true && second == true)) {int index = i + bit < n ? (i + bit) : (i + bit) % n;int temp = a[index];a[index] = pre;pre = temp;if (index == 0) {first = true;}if (index == 1) {second = true;}i = index;if (i == 0 && !second) {i += 1;pre = a[1];}}return a;}

2、螺旋矩阵

矩阵螺旋遍历，输入结果

思路：

1. 设置左右上下的边界

2. （i, j） 表示当前判断元素， 将i 、j和上下左右边界做判断

3. 按照 右走 、下走、左走、上走的顺序， 在每个方向上做判断

4. 在往每个方向走的时候，判断是否能走， 如果不能走，则终结。

    public ArrayList<Integer> spiralOrder(int[][] matrix) {if(matrix == null || matrix.length <= 0 ){return new ArrayList<>();}int m = matrix.length;int n = matrix[0].length;int upI = 0;int downI = m-1;int leftJ = 0;int rightJ = n-1;int i =0, j=0;ArrayList<Integer> list = new ArrayList<>();while (i >= upI && i <= downI && j >= leftJ && j <= rightJ){// 往右走if(j> rightJ){break;}while (j <= rightJ){list.add(matrix[i][j++]);}upI = upI + 1;j = j-1;i++;// 往下走if(i > downI){break;}while (i<= downI){list.add(matrix[i++][j]);}i = i-1;rightJ = rightJ -1;j--;// 往左走if(j < leftJ){break;}while (j>= leftJ){list.add(matrix[i][j--]);}j = j+1;downI = downI - 1;i--;// 往上走if(i < upI){break;}while (i>= upI){list.add(matrix[i--][j]);}i = i+1;leftJ = leftJ +1;j++;}return list;}

3、矩阵旋转90度

要求：空间复杂度 O(N2)O(N2)，时间复杂度 O(N2)O(N2)

进阶：空间复杂度 O(1)O(1)，时间复杂度 O(N2)O(N2)

思路1： 以空间换时间， 这种写起来比较简单，如果空间复杂度O(1)(1)要稍微麻烦些

新的第n行对应原来的第n列， 新的第n列和原来的第n行的方向相反。

public int[][] rotateMatrix (int[][] mat, int n) {int[][] mat1 = new int[n][n];for(int j = 0; j <n; j++){int w = 0;for(int i = n-1; i >=0; i--){mat1[j][w++] = mat[i][j] ;}}return mat1;}

4、 LRU缓存模拟

描述

设计LRU(最近最少使用)缓存结构，该结构在构造时确定大小，假设大小为 capacity ，操作次数是 n ，并有如下功能:
1. Solution(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
2. get(key)：如果关键字 key 存在于缓存中，则返回key对应的value值，否则返回 -1 。
3. set(key, value)：将记录(key, value)插入该结构，如果关键字 key 已经存在，则变更其数据值 value，如果不存在，则向缓存中插入该组 key-value ，如果key-value的数量超过capacity，弹出最久未使用的key-value

提示:
1.某个key的set或get操作一旦发生，则认为这个key的记录成了最常使用的，然后都会刷新缓存。
2.当缓存的大小超过capacity时，移除最不经常使用的记录。
3.返回的value都以字符串形式表达，如果是set，则会输出"null"来表示(不需要用户返回，系统会自动输出)，方便观察
4.函数set和get必须以O(1)的方式运行
5.为了方便区分缓存里key与value，下面说明的缓存里key用""号包裹

数据范围:

1≤capacity<=1051≤capacity<=105
0≤key,val≤2×109 0≤key,val≤2×109 
1≤n≤1051≤n≤105

思路：

1. 要求函数set和get必须以O(1)的方式运行， 所以想到用HashMap存储

2. 缓存要求有容量和大小， 所以想到用List集合存储， 并定义表示容量和大小的变量

3. get元素，按照LRU缓存特性，需要将整个元素放到集合首部

4. set元素，如果已经存在，则更新整个值，并放到首部

5. set元素，如果不存在，且size<capacity, 则放入且放到首部， size+1

6.. set元素，如果不存在，且size=capacity, 则移除最久的那个元素，当前元素加入队首

重点：同时利用HashMap+List实现LRU缓存， 另外注意并发安全， Map和List都选择并发安全的结构。

import java.util.*;
import java.util.concurrent.ConcurrentHashMap;
import java.util.concurrent.CopyOnWriteArrayList;public class LRUSolution {int LRUCapacity;int size;List<Node> list;ConcurrentHashMap<Integer, Integer> map;public LRUSolution(int capacity) {LRUCapacity = capacity;list = new CopyOnWriteArrayList<>();map = new ConcurrentHashMap<>();size = 0;}public int get(int key) {if(map.get(key) != null){deleteNode(list, key);setHeadNode(list, key, map.get(key));return map.get(key);}return -1;}public void set(int key, int value) {// 已存在元素if(map.get(key) != null){// 1. 重新设置值map.put(key, value);// 2. 删除原有key的NodedeleteNode(list, key);// 3. 设置新的头节点setHeadNode(list, key, value);return;}// 不存在元素if(size < LRUCapacity){map.put(key, value);list.add(0, new Node(key, value));size++;}else{// 1. 删除一个最久的元素Node lastNode = list.get(list.size()-1);map.remove(lastNode.key);deleteLastNode(list);// 2. 设置新的头节点setHeadNode(list, key, value);map.put(key,value);}}/*** 将key和value设置成新的头节点* @param list* @param key* @param value*/private void setHeadNode(List<Node> list, int key, int value) {list.add(0, new Node(key, value));}/*** 删除原有key* @param list* @param key*/private void deleteNode(List<Node> list, int key) {if(list.size() <= 0){return;}for(Node node : list){if(node.key == key){list.remove(node);}}}/*** 删除最久的Node** @param list*/private void deleteLastNode(List<Node> list) {if (list.size() <= 0) {return;}list.remove(list.size() - 1);}static class Node{int value;int key;public Node(int key,int value) {this.value = value;this.key = key;}}public static void main(String[] args) {// ["set","set","set","get","get"],[[1,1],[2,2],[1,3],[1],[1]],3// 预期：["null","null","null","3","3"]// 实际：LRUSolution lruSolution = new LRUSolution(2);lruSolution.set(1, 1);lruSolution.set(2, 2);lruSolution.set(1, 3);lruSolution.get(1);lruSolution.get(1);}
}

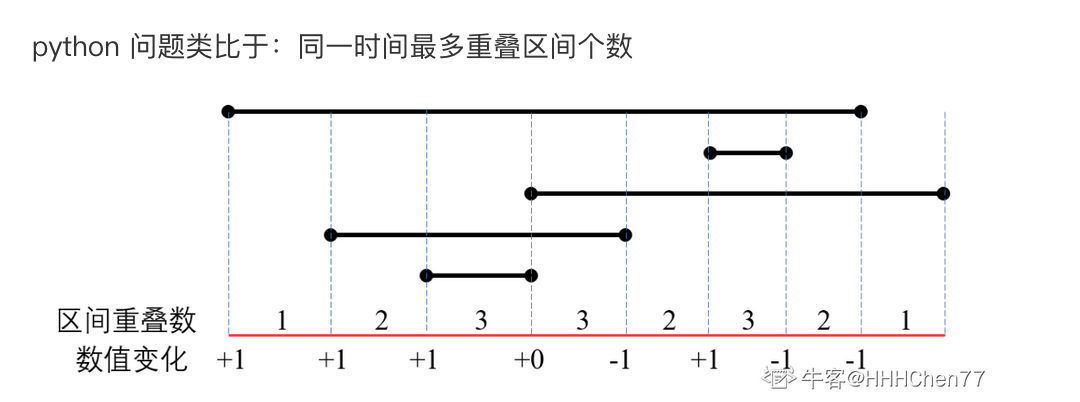
5、需要多少主持人

有 n 个活动即将举办，每个活动都有开始时间与活动的结束时间，第 i 个活动的开始时间是 starti ,第 i 个活动的结束时间是 endi ,举办某个活动就需要为该活动准备一个活动主持人。

一位活动主持人在同一时间只能参与一个活动。并且活动主持人需要全程参与活动，换句话说，一个主持人参与了第 i 个活动，那么该主持人在 (starti,endi) 这个时间段不能参与其他任何活动。求为了成功举办这 n 个活动，最少需要多少名主持人。

数据范围: 1≤n≤1051≤n≤105 ， −232≤starti≤endi≤231−1−232≤starti​≤endi​≤231−1

复杂度要求：时间复杂度 O(nlog⁡n)O(nlogn) ，空间复杂度 O(n)O(n)

思路1：

    public int minmumNumberOfHost2(int n, int[][] startEnd) {Long[] start = new Long[n];Long[] end = new Long[n];for(int i = 0; i < n; i++){start[i] = Long.valueOf(startEnd[i][0]);end[i] = Long.valueOf(startEnd[i][1]);}Arrays.sort(start);Arrays.sort(end);int i = 0, j= 0;int count = 0;int maxCount = 0;while (i <n && j < n){// 新活动开始if(start[i] < end[j]){count++;i++;maxCount = Math.max(maxCount, count);}// 当前活动开始时间和上个活动结束时间一致else if(start[i]  ==  end[j]){i++;j++;}// 一个活动结束else{j++;count= count-1;}}return maxCount;}

思路2：

1. 时间区间排序，注意用Long类型表示，虽然数据范围有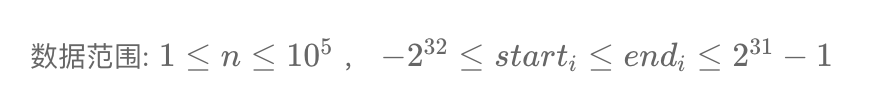

实际给出的测试用例有2147483648， 实际上最大值是2147483647（2^31 - 1）

2. 用集合记录下每个主持人结束时间

3. 判断当前时间区间是否有剩余空闲主持人，没有的话新找一个人(num++)

缺点：报错超时

    public int minmumNumberOfHost(int n, int[][] startEnd) {if (n == 0 || n == 1) {return n;}List<Interval> intervalList = new ArrayList<>();for (int i = 0; i < n; i++) {intervalList.add(new Interval(Long.valueOf(startEnd[i][0]),Long.valueOf( startEnd[i][1])));}intervalList.sort((o1, o2) -> {if (o1.start == o2.start) {return o1.end - o2.end > 0 ? 1 : (o1.end == o2.end ? 0 : -1);} else {return o1.start - o2.start > 0 ? 1 : -1;}});List<Long> endNumList = new ArrayList<>();int num = 1;for (int i = 1; i < intervalList.size(); i++) {// 出现交集if (intervalList.get(i).start < intervalList.get(i - 1).end) {// 记录上一个人的结束时间endNumList.add(intervalList.get(i - 1).end);Arrays.sort(new List[]{endNumList});endNumList.sort((o1, o2) -> o1 - o2 > 0 ? 1 : (o1 == o2 ? 0 : -1));// 判断是否有空闲的人 主持当前时间段if (endNumList.size() > 0 && endNumList.get(0) <= intervalList.get(i).start) {endNumList.remove(0);} else {num++;}}}return num;}public static class Interval {Long start;Long end;public Interval(Long start, Long end) {this.start = start;this.end = end;}}

http://www.dtcms.com/a/474153.html

相关文章：

  • 多线程 —— CAS 原理
  • 兰州做网站的有哪几个网站后台登陆不了
  • css实现表格中最后一列固定
  • 优秀原创设计网站门户系统设计
  • linux环境docker如何让启动的容器在后台运行
  • 软考架构师高分避坑指南：三科实战拆解与破局之道
  • 新手向C语言JavaPython 的选择与未来指南
  • 摄影网站难做吗网站如何集成微信支付
  • Redis5安装与核心命令详解
  • 单个请求中同时使用 multipart/form-data 和 application/json 的可行性及正确实现方式
  • wordpress网站配置甜妹妹福利wordpress
  • 新奇的Word表格单元格合并
  • 网站建设模板系统网站漂浮广告怎么做
  • 【如何解决“支付成功，但订单失败”的分布式系统难题？】
  • MQTT系列（三）
  • app开发流程表北京网站优化快速排名
  • 衡石科技嵌入式BI：重构企业应用的数据智能生态
  • rdd数据存储在spark内存模型中的哪一部分
  • 肥西县重点工程建设管理局网站支付宝 收费 网站开发
  • [webgl]基于THREEJS开发的sdk，使开发三维效果更加的容易
  • [Java、C语言、Python、PHP、C#、C++]——深度剖析主流编程语言的核心特性与应用场景
  • Deployment 和 StatefulSet 的区别
  • 广州自助网站制作网站开发成app
  • LeetCode 396 - 旋转函数 (Rotate Function)
  • 服装公司网站策划书网站无法连接服务器
  • 【C++篇】：LogStorm——基于多设计模式下的同步异步高性能日志库项目
  • php怎么做网站怎么做试玩平台推广网站
  • go语言：在 Win10上，如何编译 ffuf-v2.1.0？
  • 做网站没装数据库建站 网站程序
  • 有哪些做高考模拟卷的网站做第一个网站什么类型