AI学习日记——卷积神经网络(CNN):完整实现与可视化分析
目录
一、SimpleConvNet的完整实现
1. 网络架构设计
2. 参数初始化策略
3. 层的有序组织
4. 前向与反向传播
二、CNN的可视化分析
1. 第一层权重可视化
2. 特征提取层次分析
3. 从边缘到抽象的信息流
三、经典CNN网络架构
1. LeNet
2. AlexNet
3. 网络演进的深层意义
总结
一、SimpleConvNet的完整实现
1. 网络架构设计
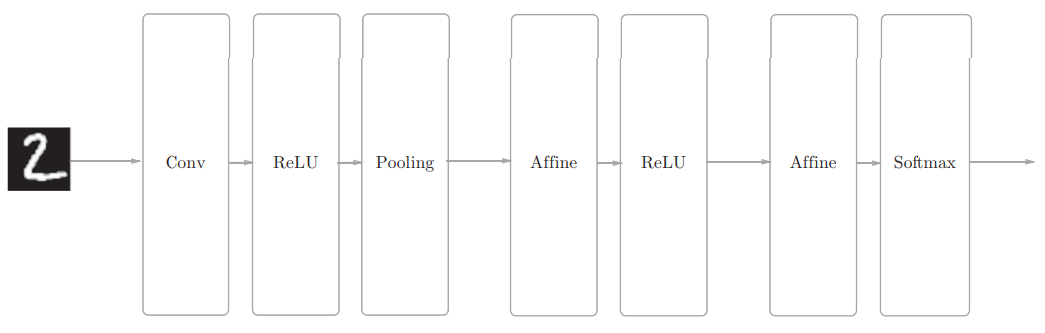
网络参数配置:
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
参数说明:
-
input_dim:输入数据维度(通道, 高, 宽)
-
conv_param:卷积层超参数字典
-
filter_num―滤波器的数量
-
filter_size―滤波器的大小
-
stride―步幅
-
pad―填充
-
-
hidden_size:全连接层神经元数量
-
output_size:输出层神经元数量
-
weitght_int_std: 初始化时权重的标准差
2. 参数初始化策略
关键计算:卷积输出尺寸
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
权重初始化:
self.params = {}
# 卷积层权重: (滤波器数, 输入通道, 滤波器高, 滤波器宽)
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num) # 每个滤波器一个偏置# 全连接层权重
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
3. 层的有序组织
使用OrderedDict有序字典确保层按顺序执行:
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
这里字典的value值实际上是对象实例,省略了以下步骤
1.relu1_instance = Relu()
2.self.layers['Relu1'] = relu1_instance
4. 前向与反向传播
前向传播实现:
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return xdef loss(self, x, t):
y = self.predict(x)
return self.last_layer.forward(y, t)
反向传播实现:
def gradient(self, x, t):
# 前向传播计算损失
self.loss(x, t)
# 反向传播
dout = 1
dout = self.last_layer.backward(dout)
# 反转层顺序进行反向传播
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 收集梯度
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads
二、CNN的可视化分析
1. 第一层权重可视化
通过可视化卷积层权重,我们可以直观理解CNN的训练过程:
权重形状:(30, 1, 5, 5) - 30个5×5的单通道滤波器
可视化发现:

-
学习前:随机初始化,黑白浓淡无规律
-
学习后:呈现有规律的图案,如边缘检测器和斑块检测器
具体模式:
-
白到黑渐变滤波器:检测边缘
-
块状区域(blob)滤波器:检测局部特征
2. 特征提取层次分析
CNN通过分层结构逐步提取越来越抽象的特征:
第1层 - 低级特征:
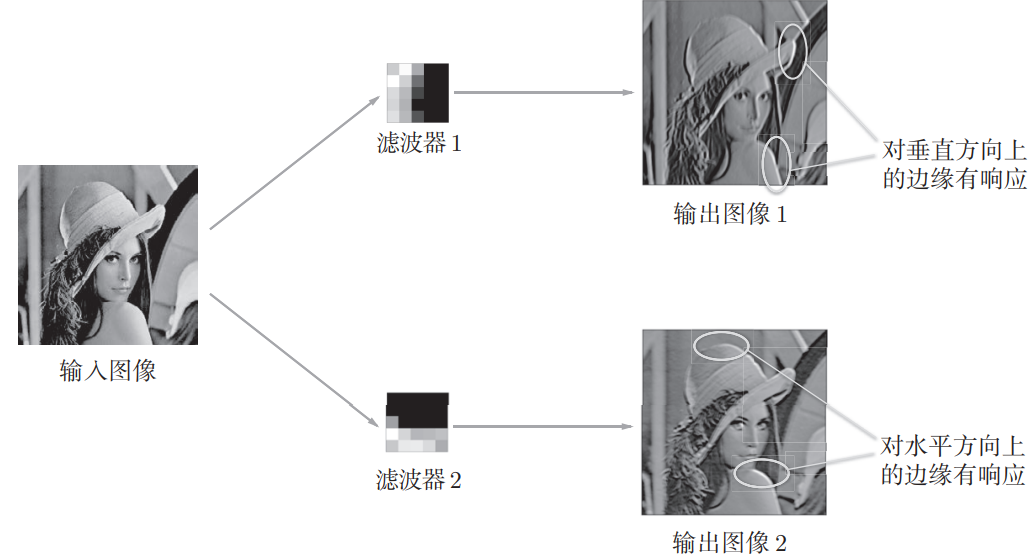
-
对边缘和斑块有强烈响应
-
如图,某些滤波器专门检测垂直边缘,某些检测水平边缘
中间层 - 中级特征:
-
对纹理和简单形状有响应
-
组合低级特征形成更复杂的模式
深层 - 高级特征:
-
对物体部件和复杂模式有响应
-
特征更加抽象和语义化
3. 从边缘到抽象的信息流
CNN的特征提取过程模拟了人类视觉系统:
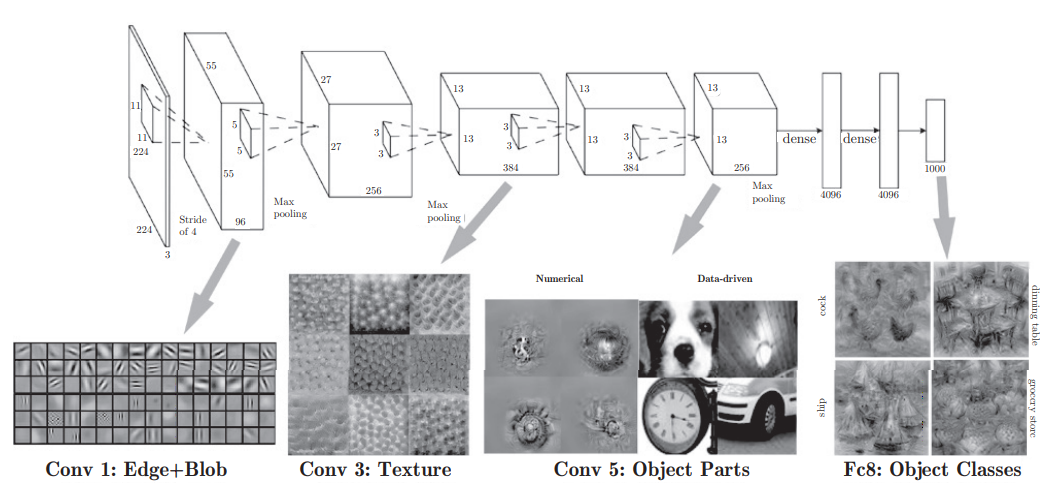
边缘/斑块 → 纹理/简单形状 → 物体部件 → 完整物体
这种层次化处理使得CNN能够:
-
对平移、旋转等变化具有鲁棒性
-
逐步构建对输入数据的复杂理解
-
实现端到端的特征学习
三、经典CNN网络架构
1. LeNet
1998年提出的LeNet是CNN的元祖,用于手写数字识别。
网络结构特点:
-
连续的卷积层和池化层(子采样层)
-
最后接全连接层输出结果
-
激活函数使用sigmoid
与现代CNN的差异:
-
激活函数:sigmoid → ReLU
-
池化方式:子采样 → Max池化
-
网络深度相对较浅
历史意义:
作为20多年前提出的网络,其基本思想至今仍在沿用,展现了惊人的前瞻性。
2. AlexNet
2012年提出的AlexNet引发了深度学习的热潮。
网络结构改进:
-
使用ReLU激活函数解决梯度消失问题
-
引入LRN(局部响应归一化)层
-
采用Dropout防止过拟合
-
网络深度和宽度大幅增加
技术环境支撑:
-
大数据:ImageNet等大规模数据集
-
GPU计算:并行计算能力的大幅提升
-
算法优化:更好的优化方法和正则化技术
性能突破:
在ImageNet竞赛中大幅超越传统方法,证明了深度学习的巨大潜力。
3. 网络演进的深层意义
从LeNet到AlexNet的演进反映了深度学习的核心发展:
数据驱动:
-
从少量数据到海量数据
-
数据成为模型性能的关键因素
计算能力:
-
从CPU到GPU的转变
-
分布式训练成为可能
算法创新:
-
更好的激活函数(ReLU)
-
更有效的正则化方法(Dropout)
-
更深的网络结构
哲学转变:
从手工设计特征转向端到端的特征学习,让数据自己"说话"。
总结
本文介绍了SimpleConvNet的完整实现和CNN的可视化分析。SimpleConvNet包含网络架构设计、参数初始化、有序组织层结构以及前向/反向传播的实现。CNN可视化分析展示了权重可视化的过程,揭示了CNN从边缘检测到抽象特征提取的层次化处理机制。最后,文章对比了LeNet和AlexNet两大经典网络架构,指出深度学习从数据驱动、计算能力到算法创新的演进历程,体现了从手工特征设计到端到端学习的范式转变。这些内容系统展示了CNN的实现原理、特征提取机制和发展脉络。
