十四,数据结构-堆
定义
堆作为一种数据结构来理解的话,也是一种树,其适合特定的场合——即优先队列这种抽象数据结构的实现。堆有不同的类型,以之前树种的二叉树为例,二叉堆也是堆的一种。二叉堆是一种特殊的二叉树,有最大堆和最小堆的区别。
二叉堆是满足下述条件的二叉树:
- 树的每个节点的数值都大于其所有后代节点的数值,这就是堆的条件;
- 树必须是完全的,即树中填满了所有节点,不存在缺失的节点,具体检查方法就是:从左向右检查每层树节点,每个节点都存在,但最下面一层允许有空位的存在,只要空位的右边没有节点就行。
举例如下,下面的二叉树最后一行空位右侧仍然有节点,因此是不完全的:

而下面这棵树,最下面一层空位右侧没有任何节点,因此是完全的
性质
堆源于二叉树,但又不同于二叉树,和二叉树相比,堆是一种弱排序的数据结构(二叉树要求其数左子树所有节点必须小于本身的数值,右子树所有节点数值必须大于本身的数值)。堆最明显的性质就是:根节点的数值总是最大的。这也是堆实现优先队列的优势。这里再补充一下优先队列的定义:相较于FIFO的一般队列,优先队列要求插入时必须按序插入,而不仅仅是从队列末端插入。
操作
堆的主要操作有:插入和删除。删除在头部进行,插入在尾部进行(堆的为节点即树的最下一层最右侧的节点)。
插入
插入步骤如下:
- 创建新节点,存储新值,插入最下层右边空缺的第一个位置,该节点即堆的尾节点;
- 比较新节点和父节点数值大小;
- 如果新节点数值大于父节点数值,则交换双方位置;
- 重复步骤3,把新节点向上移动,直到父节点的数值大于新节点数值(这个移动的过程被叫做上滤)。
从上述步骤中可以看出,该插入操作的效率为O(logN),N为节点数,因为二叉树如果有N个节点,则大约有logN层。
上述步骤看似简单,但还有个困难,即如何寻找右边空缺的第一个位置,即所谓的尾节点?其实可以通过数组来实现,即可以将二叉堆的数据存进数组(或是标准STL容器中),放置的方法即根节点位于索引0处,然后按照从左到右,从上到下的顺序依次存放,这样就能保证数组的最后一个元素总是尾节点。如下图:
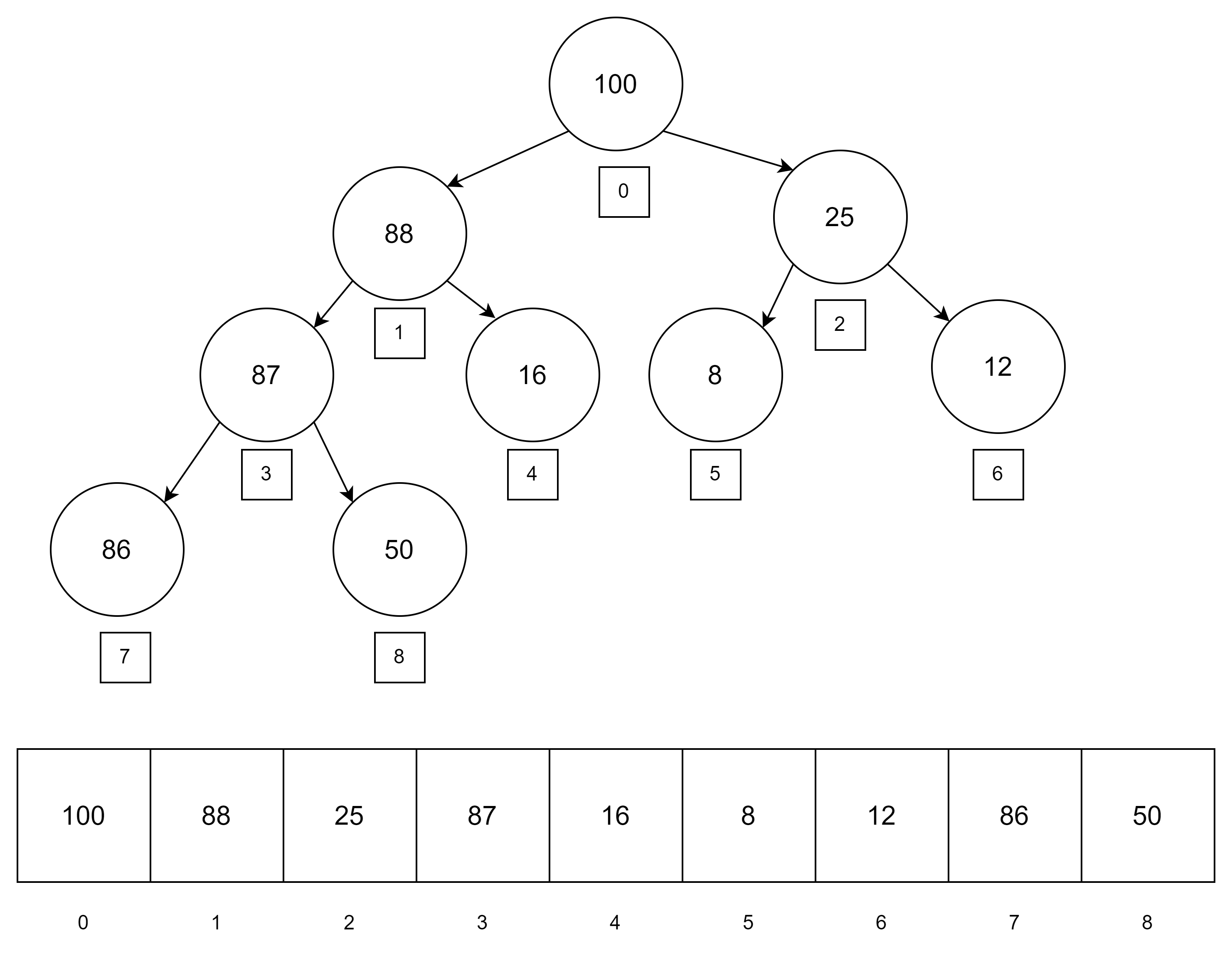
由于通过数组实现堆,这就引出了第二个问题:堆的插入和删除算法需要上滤或者下滤节点,即需要按照每个节点的链接移动,怎么移动?还是需要结合数组的索引,方法如下(结合图):
- 节点左子结点用公式:(index * 2) + 1表示;
- 节点右子结点用公式:(index * 2) + 2表示;
同时,基于数组的堆,其节点的父节点可以用:(index - 1)/ 2表示(向下取整)。
删除
堆的删除,只删除根节点,这一点和优先队列一致,即只删除优先级最高的数据,步骤如下:
- 尾节点移动到根节点位置,即覆盖/删除了原先的根节点;
- 根节点下滤到正确位置。
下滤步骤如下:
- 比较下滤节点的两个子节点数值的大小;
- 若下滤节点小于两个子节点中较大的,则交换下滤节点和较大的子节点;
- 重复步骤1和步骤2,直到不存在比下滤节点大的子节点为止。
和插入相同,删除的时间复杂度也是O(logN)。
实现
代码实现如下:
#include <vector>
#include <iostream>template<typename T>
class MaxHeap {
private:std::vector<T> data;void heapifyUp(int index) {while (index > 0 && data[index] > data[(index - 1) / 2]) {std::swap(data[index], data[(index - 1) / 2]);index = (index - 1) / 2;}}void heapifyDown(int index) {int size = data.size();while (true) {int largest = index;int left = 2 * index + 1;int right = 2 * index + 2;if (left < size && data[left] > data[largest]) largest = left;if (right < size && data[right] > data[largest]) largest = right;if (largest != index) {std::swap(data[index], data[largest]);index = largest;} else break;}}public:void push(const T& value) {data.push_back(value);heapifyUp(data.size() - 1);}void pop() {if (data.empty()) return;data[0] = data.back();data.pop_back();heapifyDown(0);}T top() const {return data.empty() ? T() : data[0];}bool empty() const {return data.empty();}int size() const {return data.size();}
};用堆实现优先队列,其插入和删除都只需要O(logN)步,非常迅速,相较有序数组实现优先队列,需要O(N)步,堆的弱排序正是其优点。

