【第十七周】机器学习笔记06

摘要

本周学习了梯度下降在逻辑回归中的应用，并讨论了过拟合问题及其解决方法。梯度下降通过迭代优化参数最小化成本函数，逻辑回归与线性回归的梯度下降形式相似但函数定义不同。过拟合指模型过度拟合训练数据而泛化能力差，可通过收集更多数据、减少特征或正则化来解决。正则化通过修改代价函数惩罚较大参数值，减少过拟合风险，适用于线性回归和逻辑回归。

Abstract

This week I studied the application of gradient descent in logistic regression and discusses the overfitting issue along with its solutions. Gradient descent iteratively optimizes parameters to minimize the cost function; while similar in form to linear regression, logistic regression differs in its function definition. Overfitting occurs when a model fits the training data too closely, reducing generalization, and can be addressed by collecting more data, reducing features, or applying regularization. Regularization modifies the cost function to penalize large parameter values, mitigating overfitting in both linear and logistic regression.

一、梯度下降的实现

为了适配逻辑回归模型的参数，我们将尝试找到能够最小化参数w和b的成本函数j值的参数w和b，我们将再次应用梯度下降来实现这个目标，在本节中，我们将会把重点放在如何找到一个合适的参数w和b的选择，完成这些以后，如果我们给模型一个新的输入x，比如一家医院的新患者，带有一定的肿瘤大小和年龄需要诊断，模型就可以做出预测，或者尝试估计标签y为1的概率。

我们可以使用的最小化成本函数的算法是梯度下降

回顾一下成本函数

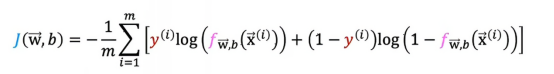
所以如果我们想最小化作为w和b的函数j，下面两个是常见的梯度下降算法

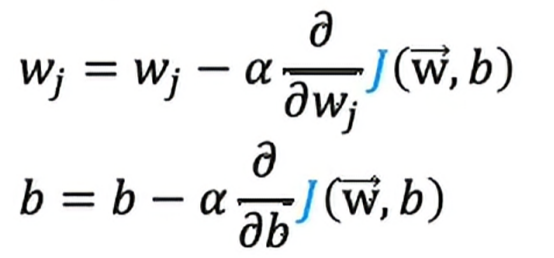
这边的偏导数我们在之前的学习中已经推导过，现在在这里不予赘述，我们在把这些式子联立后，得到了逻辑回归的梯度下降

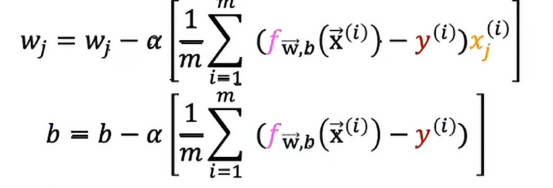
现在我们看到这两个式子可能会有个疑问，这跟我们之前学习的线性回归设计的算法一模一样，线性回归实际上和逻辑回归是一样的么？

虽然这些式子看着相同，但这不是线性回归，原因是因为函数f的定义已经被改变了

在线性回归中，f的定义为

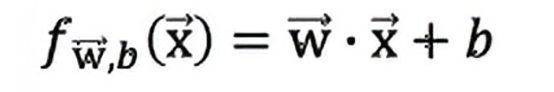
在逻辑回归中，f的定义为

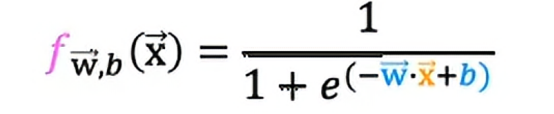
这是我们之前提到过的sigmoid函数，所以我们可以明显看到，虽然书写的算法对于线性回归和逻辑回归看起来是一样的，其实它们是两个非常不同的算法，因为我们对f的定义不同

当我们谈到线性回归的梯度下降时，我们可以看到如何监控梯度下降以确保它收敛，我们可以用同样的方法应用于逻辑回归以确保它也收敛

类似于线性回归的矢量化实现，我们可以使用矢量化使逻辑回归的梯度下降运行的更快

二、过拟合问题

现在我们看到了几种不同的学习算法，它们在很多任务上表现良好，但有时在应用中，算法可能会遇到一个称为过拟合的问题，这会导致其表现不佳，还有一个密切相关却几乎相对的现象，我们称为欠拟合

1、过拟合

为了帮助我们更好的理解什么是过拟合，我们来举几个例子，回到我们最初的通过线性回归预测房价的例子，我们想预测房价作为房屋大小的函数，我们来看一个线性回归的例子，假设我们的数据集是这样的

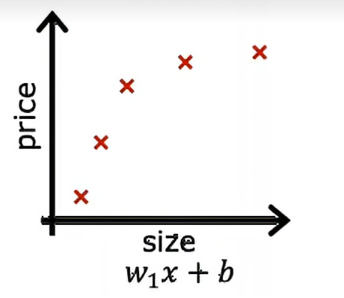
输入特征x是房屋的大小，输出y是试图预测的房价，我们可以做的一件事是为这些数据拟合一个线性函数，如果这样做，会得到一条直线拟合数据，可能看起来会这样

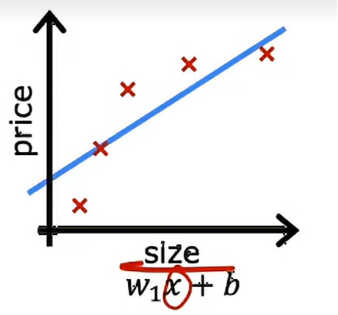
从数据上来看，似乎很明显，当房屋的大小增加时，房价会趋于稳定，所以这个算法无法很好地拟合训练数据，专业上说，就是模型对训练数据的拟合不足，另一个术语是算法有高度偏差

现在我们来看模型的第二种情况，也就是我们用两个特征对数据拟合一个二次函数，那我们可以得到一个更加符合数据分布的模型

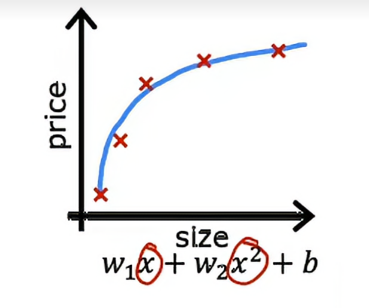
如果我们还得到一个不在这五个训练样本中的新房子，这个模型也能很好地预测新房子的价格，所以如果我是一个房地产经纪人，我是希望我的算法能够尽可能的好，即使在不属于训练集的例子上也是如此，这就叫泛化，从技术的角度上来说，我希望我的学习算法能够很好地泛化，这意味即使在从未见过的全新例子上也能做出良好的预测，所以这个二次模型似乎并不能完美地拟合训练集，我认为它能够很好地泛化到新例子

现在我们来看一个极端的例子，如果我们拟合的是一个四阶多项式到数据呢，实际上我们可以拟合出一条准确通过所有五个训练样本

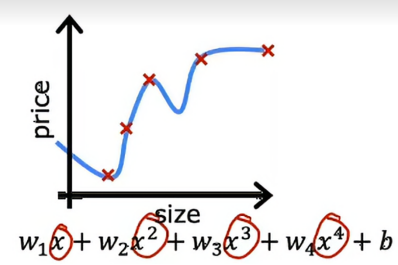
这个模型似乎在拟合训练数据上做的非常好，因为它完美的通过了所有的训练数据，实际上，我们能够选择参数，使得成本函数确实等于0，因为所有五个训练例子的误差为0，但是它上下波动的很厉害，如果我们有这个房子的大小在这里，模型会预测这个房子的价格比比它小的房子还要便宜，所以我认为这个模型并不是一个特别好的预测房价的模型，术语就是我们之前提到的过拟合了数据或者这个模型有过拟合的问题，因为尽管它非常好地拟合了训练集，但它几乎过于完美地拟合了数据，导致它的推广性得到大大的降低，我们设计出这个模型，不是为了仅仅迎合目前训练集的要求，如果我们之后加入其他的例子，它却不能很好地预测，那我们设计出这个模型就是不好的、失败的，这不符合我们设计的目的，另一个专业上的说法是有高波动、高方差，在机器学习中，过拟合和高方差几乎是可以等量替换的。

事实证明，如果我们的训练集稍微有一点不同，假设一栋房子的价格稍微高一点，稍微低一点，那么算法拟合的函数可能会完全不同。

所以我们可以说机器学习的目标是找一个既不欠拟合也不过拟合的模型，其实就是我们刚才提到的第二个模型，并不需要非常精确地拟合我们训练集上每一个数据，但是需要我们能够推广、泛化到更多的训练集上，这样才能设计出一个可以面对多种情况并能准确预测数据的模型。

2、解决过拟合

现在我们的问题是，如果发生了过拟合，我们应该如何解决？

假设我们拟合了一个模型，但它有很高的方差

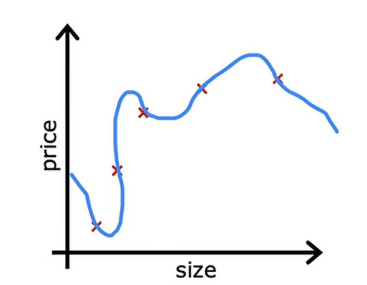
2.1、收集更多的训练数据

这是一个选项，如果我们能获得更多的数据，即更多关于房屋尺寸和价格的训练样本，那么随着训练集的增大，学习算法将拟合成一个不那么摆动的函数，于是我们可以继续拟合高阶多项式或其他具有很多特征的函数，如果有足够的训练样本，如下图所示

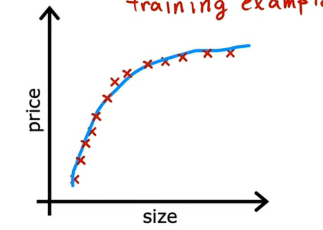
所以总结一下，我们可以用来对付过拟合的首要工具就是获取更多的训练数据。

2.2、选择较少的特征

不过，增加训练数据并不总是可行的，可能在这个地方只有有限数量的房屋出售，所以我们可能搜集不到足够的数据，这样我们就可以引出第二个解决方法：选择较少的特征

上图是我们预测房价的因素，我们可以看到，除了尺寸，房屋的卧室个数、楼层、年龄、社区的平均输入、到咖啡店的距离等等一系列的因素，事实证明，如果我们有很多这样的特征，那么我们的学习算法很可能会过拟合，现在我们舍弃一些不重要的参考因素，只选择几个占比重的，比如房屋的尺寸、卧室个数、年龄，我们可能就会发现我们的模型不会过拟合，选择最合适的特征集有时也被称为特征选择，一种方法就是根据直觉选择我们认为最好的特征集。

2.3、正则化

现在第二种方法有一个缺点，就是我们舍弃的这些特征，或多或少都会对房屋价格产生价格，有时候我们并不想通过丢弃一些特征来丢弃一些信息，进而影响我们模型的预测精度，所以人们又提出第三种减少过拟合的方法，叫做正则化，关于正则化，我们会在下一小节种深入讨论，在这里我们先介绍一下正则化的概念和思路

如果我们看到一个过拟合模型，我们会发现里面的参数往往都很大，现在如果我们要去除其中的一些特征，这相当于将该参数设置为0，所以将参数设置为0相当于消除一个特征，事实证明，正则化是一种更温和地减少某些特征影响的方法，而不是去除它们，正则化鼓励的是通过每个参数对房价的影响程度大小，来确定因素前面的因数大小，如果一个特征对房价的影响大，那么其前面的参数就大，如果一个特征对房价的影响小，那么其前面的参数就小，简单来说就是调整参数值，而不必将它们设置为0

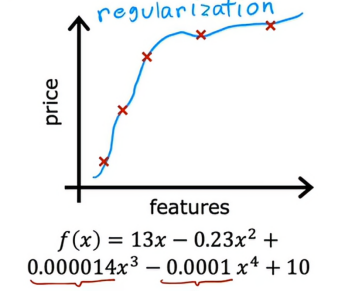
我们将刚才的例子进行正则化调整后得到的，我们发现相比于之前波动较大的情况，现在拟合的表现就很好

三、正则化代价函数

在上一个视频中，我们看到正则化试图使参数值w1到wn变小以减少过拟合，在本节中，我们将在这种直觉得基础上，为我们得学习算法开发一个修改后的代价函数，然后我们可以来实际应用正则化

回顾一下上个小节中的这个例子，我们看到如果我们对这些数据拟合一个二次函数

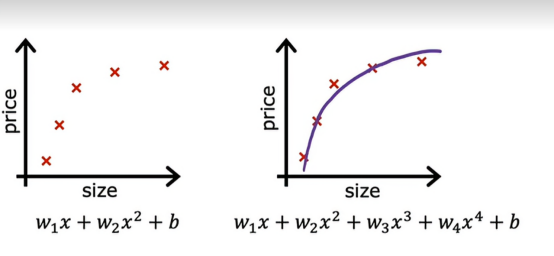
但是如果我们拟合了一个非常高次的多项式，最终会得到一条过拟合的曲线，假设我们有一种方法让参数w3和w4变得非常非常小，比如接近于零，又假设我们不是最小化这个目标函数，假设我们要修改代价函数并添加1000倍w3的平方和1000倍w4的平方

公式如下图所示

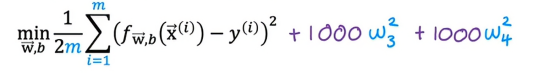
所以用这个修改后的代价函数，实际上你会惩罚模型如果w3和w4都很大，因为如果我们想要最小化这个函数，使这个新代价函数变小的唯一方法使w3和w4都很小，如果不去调整系数，这个很大的系数会影响整个代价函数，因此当你最小化这个函数时，w3将趋近于零，w4也将趋近于零，这样我们几乎取消了三次方和四次方特征的影响，如果这样做，我们得到的数据拟合将更接近于二次函数，包括可能只是来自x的三次方和四次方特征的微小贡献，这是好的，因为相比于所有参数都变大的情况，这样的数据拟合方式更好，选择了避免产生波动的二次函数

更普遍的是，这就是正则化背后的理念，如果选择的参数较小，那就有点像拥有一个更简单的模型，可能是一个特征较少的模型，因此不易产生过拟合，上面那个例子中，我们只对w3和w4进行惩罚或正则化，但更普遍的是，正则化的实现通常是在你有很多特征的情况下，比如说一百个特征，你可能不知道哪些是重要的特征，也不知道该惩罚哪些特征，所以正则化的实现方式通常是对所有的特征进行惩罚，更准确的说，是惩罚所有的wj参数，这通常会导致一个更加平滑的、更简单的、波动较小的函数，不容易产生过拟合

下面这个例子，我们建立了一个包含100个特征的模型

我们有这100个参数，从w1到w100以及第一101个参数，因为我们不知道哪些参数是重要的，哪些是不重要的，所以我们对它们都进行一些惩罚，通过添加这个项来缩小所有参数

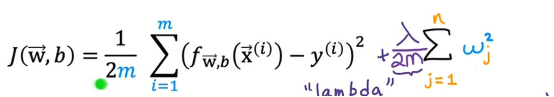
其中，n是特征数100，wj的平方和，还有λ，被称为是正则化参数，所以类似于学习率α，我们也需要为λ选择一个合适的数值

需要说明的是，这里的第一项和第二项都被缩放为1/2m，事实证明，通过同样的方式缩放这两项，选择一个合适的λ会比较简单，特别地，即使我们的训练集规模增加，比如我们的训练规模增加了，我们先前选择的λ更有可能继续工作，另外按照惯例，我们不会因为参数b增大而惩罚它，实际上，无论我们是否会这样做，差别都很小，一些机器学习工程师和学习算法工程师也会包括λ除以2m再乘以一个b的平方，但这样实际上影响不大，更常见的做法是仅对w进行正则化而不是参数b

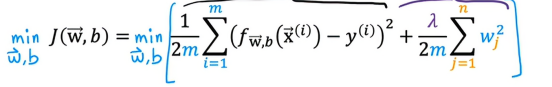
总结一下，在这个改进的损失函数中，我们要最小化原始损失，另外还有第二项，这就是所谓的正则化项，因此这个新的成本函数权衡了我们可能有的两个目标，试图最小化第一项，会鼓励算法通过最小化平方误差很好地拟合训练数据，预测值和实际值之间的差距，而试图最小化第二项，算法还试图使参数wj保持较小，这会将倾向于减少过拟合，我们选择的λ值指定了相对重要性，让我们看看λ不同会使我们的学习算法做些什么

让我们用线性回归的房价预测例子来说明

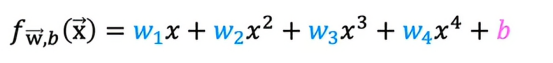
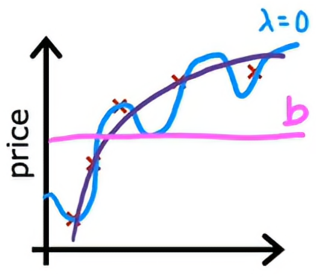
F(x)是线性回归模型，如果λ被设置为0，那么我们就完全没有使用正则化项，最终我们会拟合出一个过于摇摆，过于复杂线并且过拟合的曲线

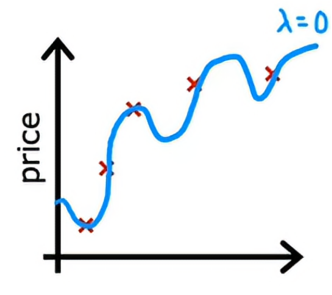
让我们来看另外一个极端的例子，如果我们将λ设置为一个非常大的数字，比如λ=1010，那么我们会在右边的正则化项上赋予非常重的权重，并且唯一能够最小化成本的方式就是确保所有w的值几乎都非常接近于0，那么这样我们就会让w1、w2、w3、w4设置成非常接近0，因此f(x)基本上等于b，因此学习算法拟合出一条水平的直线，并且出现欠拟合

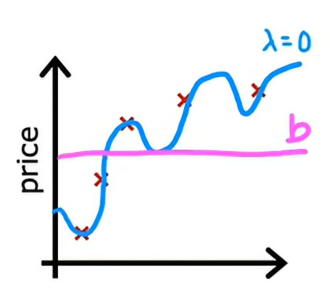
综上所述，我们所希望的是，某个介于两者之间的λ值，更恰当地平衡这个两个项，兼顾最小化均方误差和保持参数较小，当我们选择一个不大也不小的值作为λ时，我们将会得到一个非常好的曲线

1、正则化线性回归

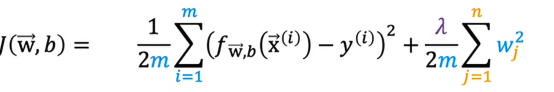
这是我们上面提出的正则化线性回归的代价函数，第一部分是常规的平方误差代价函数，现在我们有了这个额外的正则项，其中λ是正则化参数，我们希望找到最小正则化代价函数的参数w和b，之前，我们用梯度下降来处理原始代价函数，处理函数为

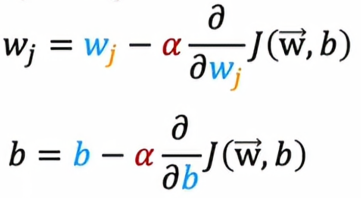
我们之前就是依照这两个公式不断更新参数w和b来实现梯度下降，事实上，正则化线性回归的更新看起来完全一样，只是现在代价函数j的定义有所不同

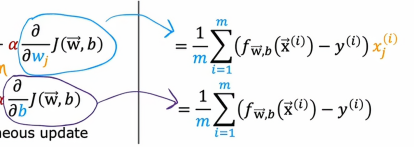
之前我们j关于wj的导数是由这个表达式给出的，j关于b的导数是由这个表达式给出的，现在我们添加了这个额外的正则项，唯一改变的是wj导数表达式多了一个附加项，即：

记住，我们不准备正则化b，所以这个关于b的梯度下降公式，我们没有加入相应的正则化项数，然后我们把这两个式子，带入到原来的梯度下降算法，这样得出来得两个式子就是正则化线性回归的梯度下降

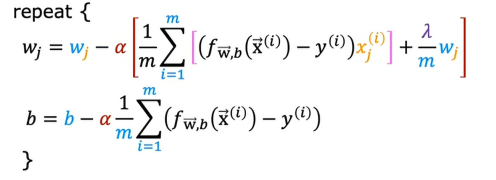
因此要实现正则化线性回归的梯度下降，这就是我们需要让代码执行的操作

接下来是对这些公式的推导，如下两图所示

2、正则化逻辑回归

正如逻辑回归的梯度更新和线性回归的梯度更新看起来惊人地相似，我们也会发现正则化逻辑回归的梯度下降更新看起来也类似正则化线性回归的更新

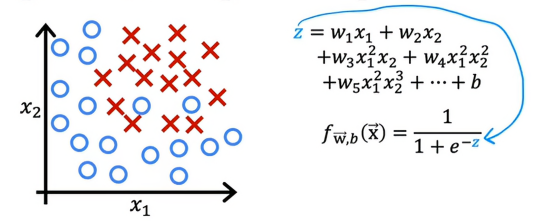
我们之前看到，如果用高阶多项式进行拟合，逻辑回归可能会容易过拟合，这里z是传递给sigmoi函数的高阶多项式，最终我们计算的话，会得到一个复杂并且过拟合到这个训练集的决策边界，更一般的，当我们使用很多特征训练逻辑回归时，无论是多项式还是其他特征，过拟合的风险会更高

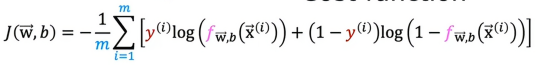
这是逻辑回归的代价函数，如果我们想用正则化来修改，只需加上正则化参数即可：

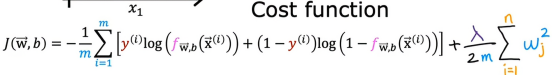
所以当我们准备最小化这个代价函数时，它会惩罚w1到wn，并防止它们变得太大，如果我们这么做，即使我们用很多参数拟合一个高阶多项式，我们仍然会得到一个合理的决策边界，这样一个合理的决策边界来确定正例和负例，同时也能泛化，希望能对训练集以外的新例子进行良好预测

3、实际最小化包含正则化项的代价函数

那么，让我们像以前一样使用梯度下降，这是你要最小化的代价函数

为了实现梯度下降，我们像以前对wj和b进行同步更新，跟上面线性回归所说的是一个道理，我们在通用的梯度下降公式后面再加了一个正则化参数

这里的f(x)定义的时逻辑回归的函数

总结

梯度下降是优化逻辑回归参数的关键算法，需注意其与线性回归的差异。过拟合是常见问题，可通过增加数据、特征选择或正则化来改善模型泛化能力。正则化通过调整代价函数有效控制参数大小，提升模型性能。