大模型前世今生（十二）：Hessian矩阵

想象我们正站在一片风景中，不是草地和山丘，而是“损失函数风景”。每个点都是模型可能拥有的一组权重，高度代表模型在那里的“错误”程度。

低谷=好，高峰=坏。

Hessain矩阵？如果说坡度（斜率）告诉你哪条路是下坡，那么 Hessian 矩阵则告诉你坡度本身是如何变化的（曲率）：

- 山谷是陡峭的还是平坦的？
- 只有一个碗状结构，还是有很多小凹陷？
- 如果你迈出一步，你会快速跌倒还是缓慢地漂移？

你手中握着的不是一根拐杖，而是一个二阶偏导数矩阵。如果你处在一个陡峭的山谷中，曲率很高，即使是很小的一步也会对损失产生很大的影响。如果你处在一个宽阔的盆地中，曲率很低，你可以四处走动，损失几乎不会改变。

这样，权重的微小变化（来自噪声、量化或不同的训练批次）不会对性能造成太大影响。模型泛化能力更强，它没有记住一个完美的位置；它找到了一个连贯解的区域。

大型模型（例如 Transformer）往往会自然地落入这些宽阔的盆地，因为参数空间巨大，近似等效配置的数量呈指数级增长，而使用噪声梯度的优化会倾向于最宽阔、最宽容的谷底。

---

矩阵可以是导数吗？是的，但不是单个数字的导数。你可以想得更远一些。

假设你有一个函数，它不只有一个变量  x ，而是多个变量：

f(x_1, x_2, …, x_n)

它的梯度是一个一阶导数向量：

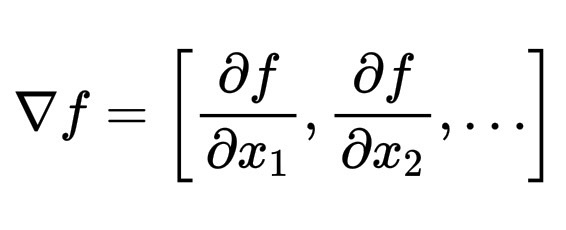
\nabla f = \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots \right]

它指向地形图中的“下坡”。

现在……Hessian就是梯度的导数，所以它是一个二阶偏导数矩阵：

 

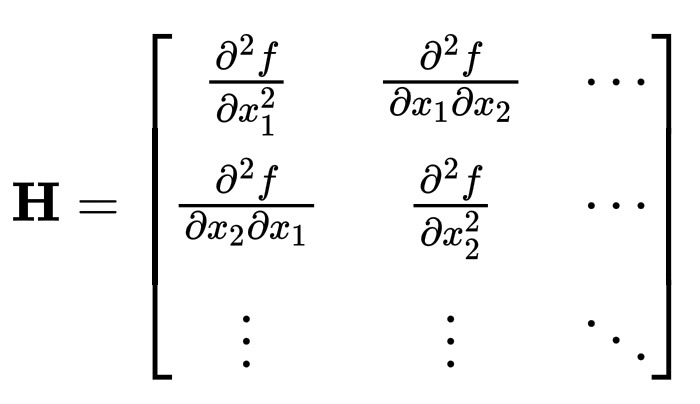
\mathbf{H} = 

\begin{bmatrix}

\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots \\

\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots \\

\vdots & \vdots & \ddots

\end{bmatrix}

其中，每个元素衡量一个方向上的斜率如何随着另一个方向的变化而变化。

那么，它是如何“知道”平坦度和凹陷度的？

让我们朝某个方向 v 迈出一小步，Hessian 矩阵告诉我们梯度如何沿着 v 变化：

- 如果 H 的所有特征值均为正：山谷向各个方向向上弯曲，形成一个漂亮的圆碗。
- 如果某些特征值为零：山谷在那个方向上是平坦的，就像一个狭长的平原。
- 如果符号混合：鞍点，就像山口。

所以 Hessian 矩阵不仅仅是数字。它是理解的形状，描述了事物如何关联的局部几何。

---

想象一个二维碗状结构：

L(\theta_1, \theta_2) = \theta_1^2 + 0.1 \, \theta_2^2

这是一个细长的浅盆地。计算它的 Hessian 矩阵：

 

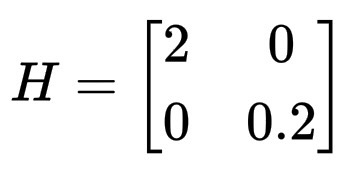
H =

\begin{bmatrix}

2 & 0 \\

0 & 0.2

\end{bmatrix}

较大的值 (2) 表示陡峭方向，较小的值 (0.2) 表示平坦方向，模型可以在第二个方向上移动很远而不会对损失产生太大影响。