【双机位A卷】华为OD笔试之【模拟】双机位A-新学校选址【Py/Java/C++/C/JS/Go六种语言】【欧弟算法】全网注释最详细分类最全的华子OD真题题解

可上 欧弟OJ系统 练习华子OD、大厂真题
绿色聊天软件戳 od1441了解算法冲刺训练（备注【CSDN】否则不通过）

相关推荐阅读

• 【华为OD机考正在更新】2025年双机位A卷真题【完全原创题解 | 详细考点分类 | 不断更新题目 | 六种主流语言Py+Java+Cpp+C+Js+Go】
• 【华为OD机考】2025C+2025B+2024E+D卷真题【完全原创题解 | 详细考点分类 | 不断更新题目】
• 【华为OD笔试】双机位A+2025C+2025B+2024E+D卷真题机考套题汇总【真实反馈，不断更新，限时免费】
• 【华为OD笔试】2024E+D卷命题规律解读【分析500+场OD笔试考点总结】
• 【华为OD流程】性格测试选项+注意事项】

题目练习网址：【模拟】双机位A-新学校选址

题目描述与示例

题目描述

为了解新学期学生暴涨的问题，小乐村要建立所新学校，考虑到学生上学安全问题，需要所有学生家到学校的距离最短。

假设学校和所有学生家都走在一条直线之上，请问学校建立在什么位置，能使得到学校到各个学生家的距离和最短。

输入描述

第一行: 整数 n 取值范围 [1, 1000]，表示有n户家庭。

第二行: 一组整数 m 取值范围 [0, 10000] ，表示每户家庭的位置，所有家庭的位置都不相同。

输出描述

一个整数，确定的学校的位置。如果有多个位置，则输出最小的。

示例一

输入

5
0 20 40 10 30

输出

20

说明

20到各个家庭的距离分别为20 0 20 10 10，总和为60，最小

示例二

输入

1
20

输出

20

说明

只有一组数据，20到20距离最小，为0

示例三

输入

2
0 20

输出

0

说明

有多个地方可选，但是0数值最小

解题思路

这题乍一看非常复杂。

一个非常直接的暴力解思路如下：穷举出所有位置并且分别计算这些位置到所有点的距离总和再取其最小值。

由于这些家庭的位置取值范围为[0, 10000]，所以一共需要枚举m = 10000个点。

家庭数量n的最大值为1000，如果这m个点都去计算到n个点的距离总和，那么这种暴力解的时间复杂度为O(nm) = O(10^7)，一定会超时。

这实际上是一个非常简单的数学问题，需要先进行一定的逻辑推理后再进行具体的代码编写。

仅两个点的简单情况

考虑只有两个点的简单情况。

设这两个点的值分别为a0和b0（不妨假设a0 < b0成立，即a0在b0的左边）

显然，当我们所选取的点P位于这两个点之间的时候，所选无论P如何移动，点P到a0和点P到b0之间的距离和为一个定值b0-a0。

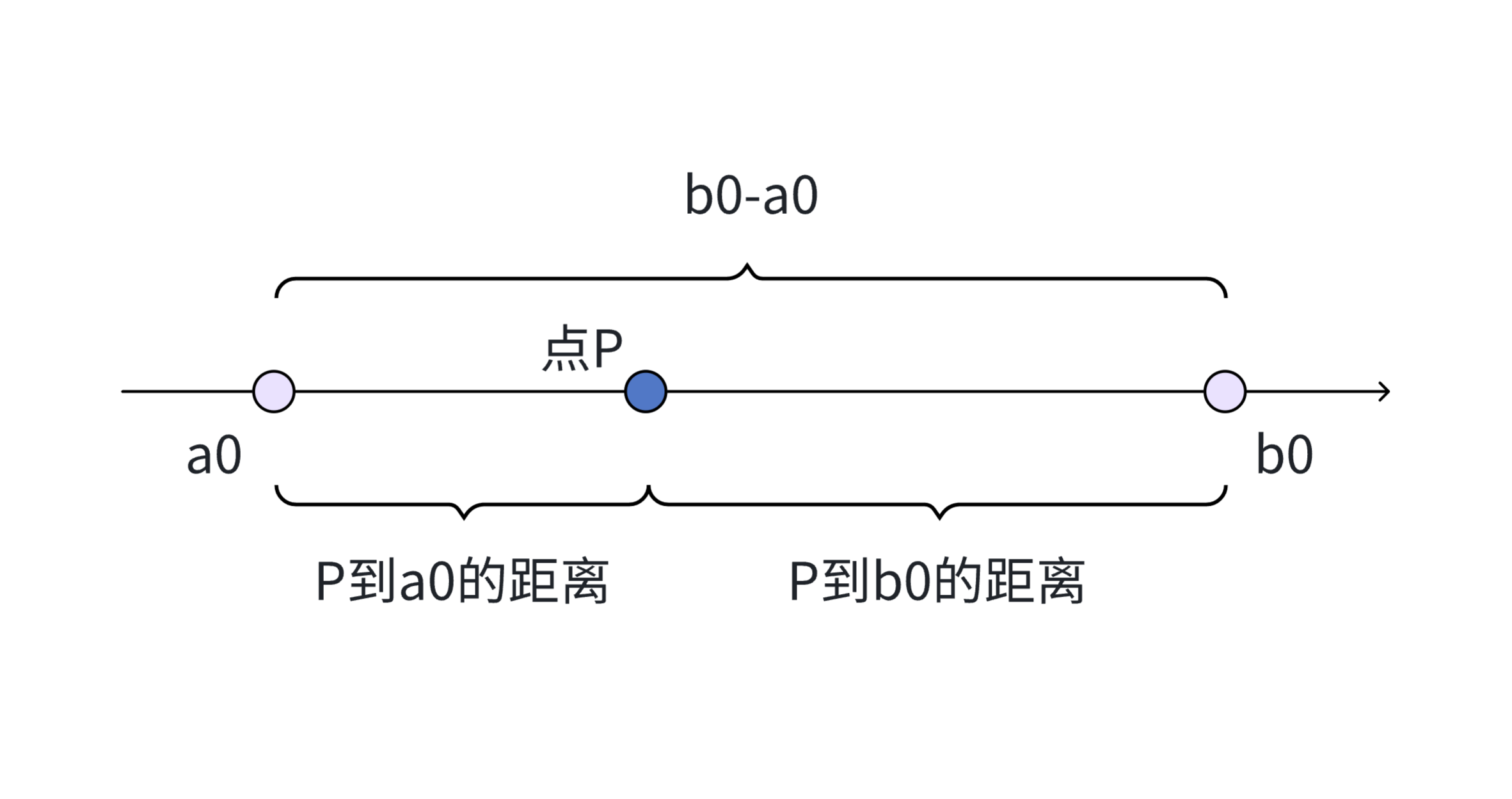
显然，当点P位于在a0左边，或者点P位于b0右边的时候，即点P位于这两个点外部的时候，点P到两点的距离和一定会超过定值b0-a0。

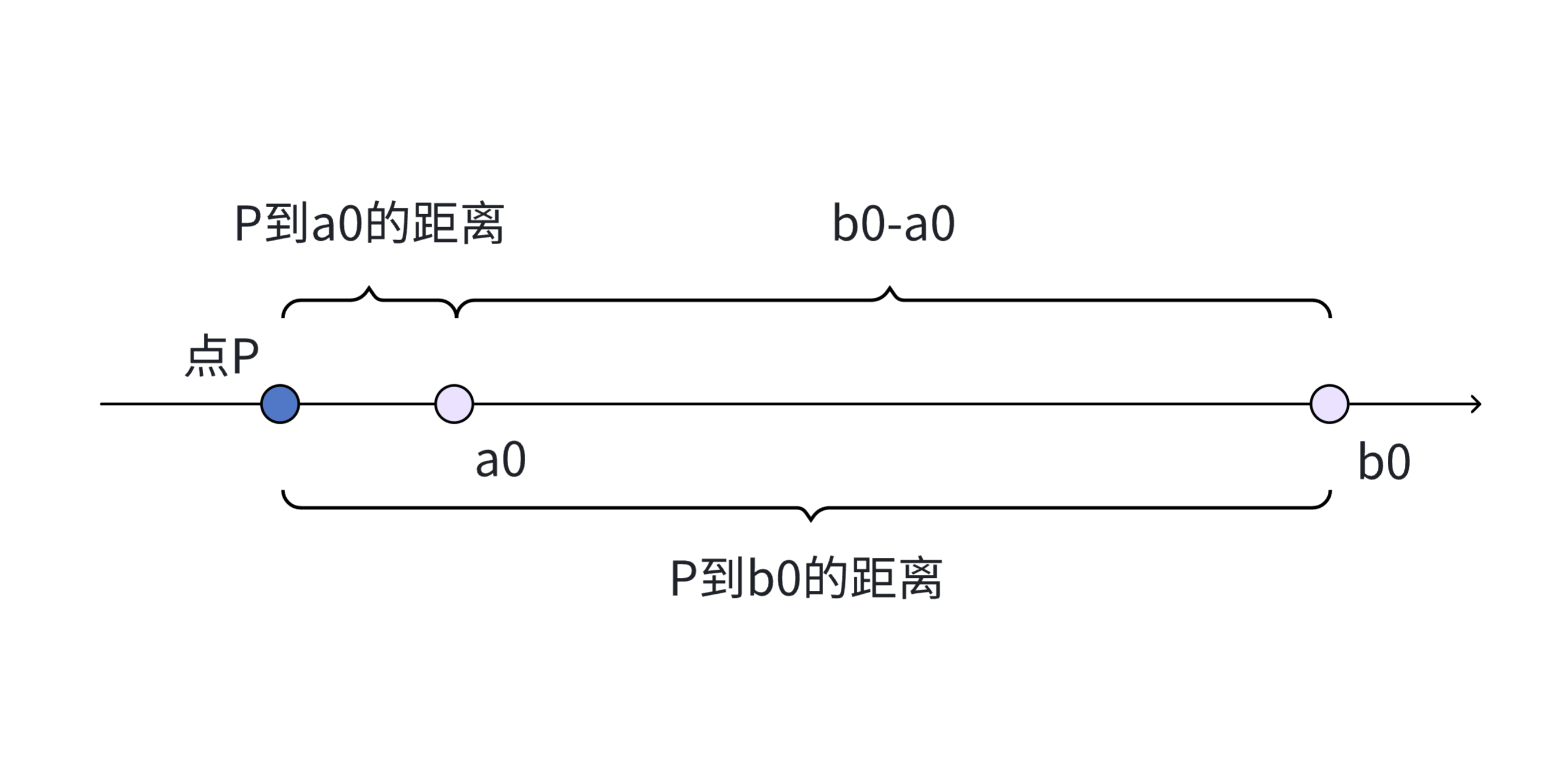
我们如果要找一个点位于a0和b0之间（可以与a0或b0重合），且要求点P的值尽可能地小，那么我们会选择令点P和a0重合。

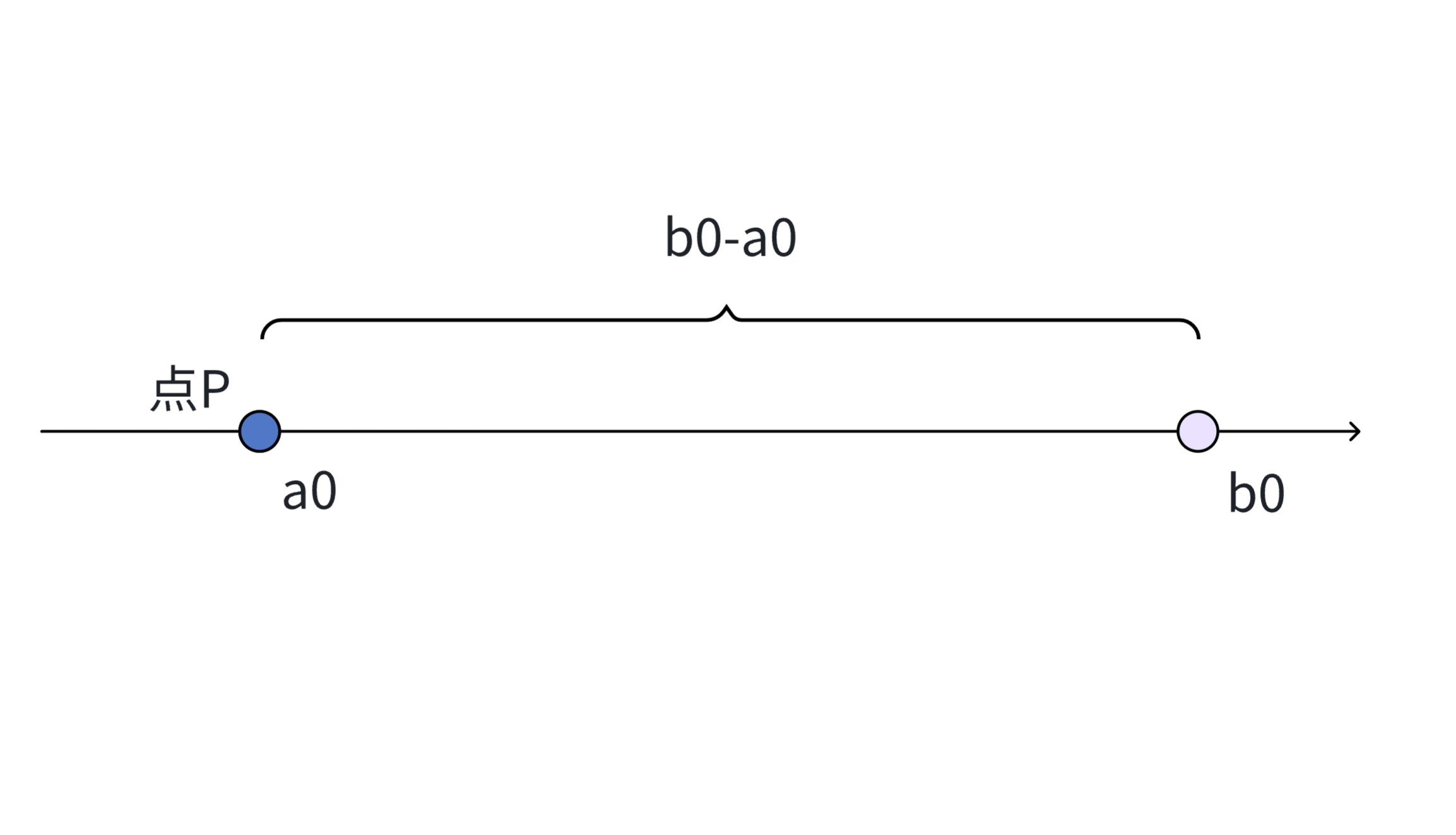
也就是示例三的情况。

拓展到偶数个点的情况

拓展到偶数个点的情况。

假设存在偶数个点，从左往右分别为am, ..., a1, a0, b0, b1, ..., bm。

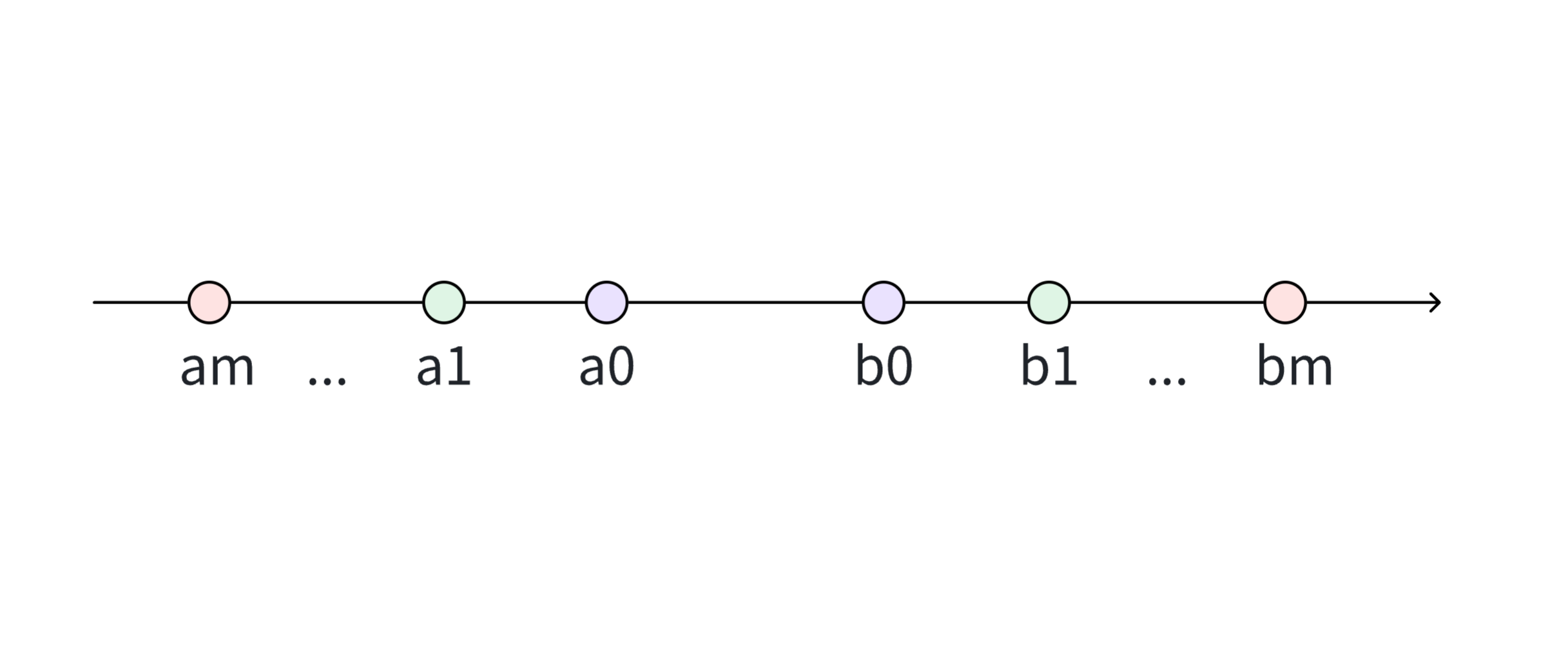
对这些点根据下标进行两两分组。

显然a0和b0是位于所有点的中间位置的，位于a0和b0之间的点P，也一定会位于其他组的两个点之间。

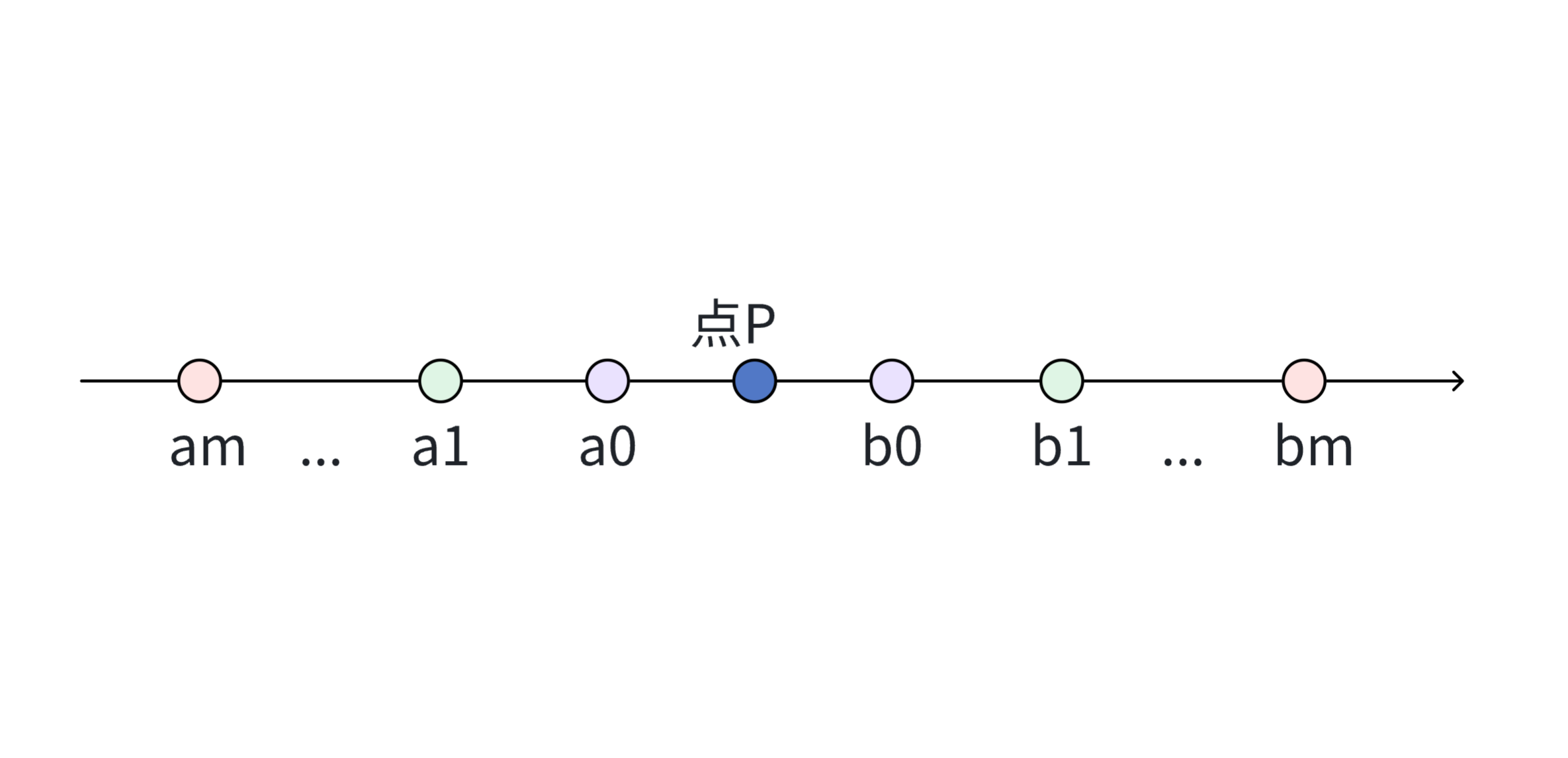
因此，当点的个数是偶数时，我们仍然选择点P和a0重合，此时点P距离所有点的距离的和也可以取到最小值，其具体的值为(b0-a0)+(b1-a1)+(b2-a2)+...+(bm-am)。

这样我们就把偶数个点的情况考虑完毕了。我们需要对整个输入数组nums进行从小到大排序，然后选择下标为n//2-1的元素作为选址的位置。

仅一个点的简单情况

这种情况非常简单，当仅存在一个点x0时，我们的点P的选址必然是和这个点重合。

也就是示例二的情况。

拓展到奇数个点的情况

将仅一个点的简单情况拓展到奇数个点的情况的过程，实际上和将仅两个点的简单情况拓展到偶数个点的情况是一样的。

假设存在奇数个点，从左往右分别为am, ..., a1, a0, x0, b0, b1, ..., bm。

除了最中间的点x0之外，其他所有点都可以进行两两分组。

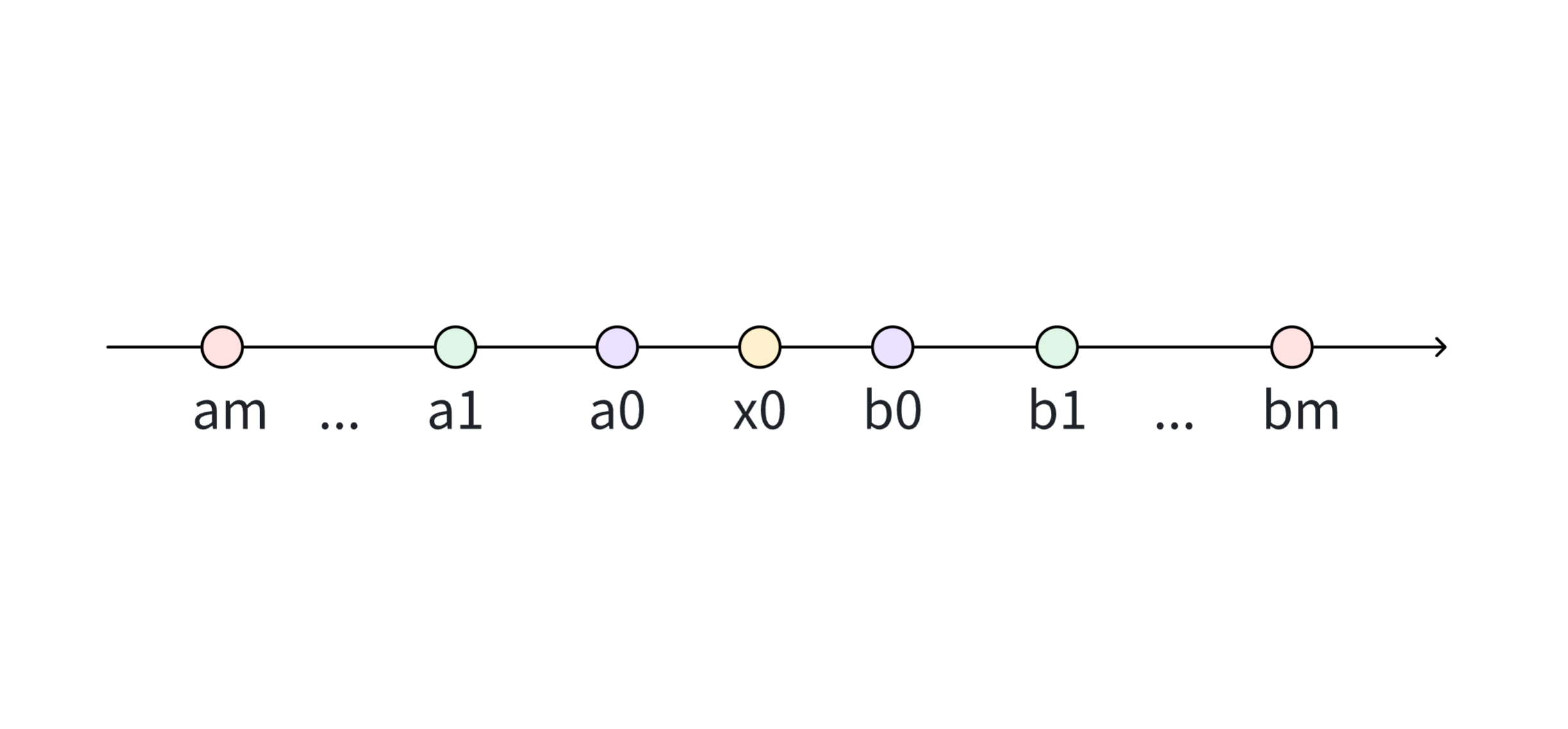
显然x0必然会位于所有的其他两两分组的点之间。

因此，当我们同样选择点P和x0重合时，此时点P距离所有点的距离的和也可以取到最小值，其具体的值也为(b0-a0)+(b1-a1)+(b2-a2)+...+(bm-am)。

这样我们就把奇数个点的情况考虑完毕了。我们需要对整个输入数组nums进行从小到大排序，然后选择下标为n//2的元素作为选址的位置，也就是选择整个数组的中位数来作为答案。

代码

Python

# 欢迎来到「欧弟算法 - 华为OD全攻略」,收录华为OD题库、面试指南、八股文与学员案例！
# 地址：https://www.odalgo.com
# 华为OD机试刷题网站：https://www.algomooc.com
# 添加微信 278166530 获取华为 OD 笔试真题题库和视频# 题目：【模拟】2025A/双机位A-新学校选址
# 分值：200
# 作者：许老师-闭着眼睛学数理化
# 算法：模拟，数学
# 代码看不懂的地方，请直接在群上提问from math import ceil# 输入点的数量
n = int(input())
# 输入数组
nums = list(map(int, input().split()))
# 对数组进行排序
nums.sort()
# 如果n是奇数，输出nums[n//2]
# 如果n是偶数，输出nums[n//2-1]
# 这两种情况可以用ceil(n/2)-1合并在一起
# 可以代入具体的数值进行验算。譬如
# n = 3时，ceil(n/2)-1 = n//2 = 1
# n = 4时，ceil(n/2)-1 = n//2-1 = 1
print(nums[ceil(n/2)-1])

Java

import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 输入点的数量int n = Integer.parseInt(sc.nextLine());// 读取并转换为整数数组int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();// 对数组进行排序Arrays.sort(nums);// 取中位数：// 若n为奇数，则为 nums[n/2]// 若n为偶数，则为 nums[n/2 - 1]// 两种情况统一写为：nums[(int)Math.ceil(n / 2.0) - 1]int median = nums[(int)Math.ceil(n / 2.0) - 1];System.out.println(median);}
}

C++

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath> // ceil()using namespace std;int main() {int n;cin >> n;vector<int> nums(n);// 输入数组for (int i = 0; i < n; ++i) {cin >> nums[i];}// 对数组进行排序sort(nums.begin(), nums.end());// 求中位数：// 奇数：nums[n/2]// 偶数：nums[n/2 - 1]// 合并写作：nums[ceil(n / 2.0) - 1]int median = nums[(int)ceil(n / 2.0) - 1];cout << median << endl;return 0;
}

C

#include <stdio.h>
#include <stdlib.h>
#include <math.h>// 比较函数，用于 qsort 排序
int compare(const void* a, const void* b) {return (*(int*)a - *(int*)b);
}int main() {int n;scanf("%d", &n); // 输入点的数量int nums[10005]; // 假设最大支持 10000 个点for (int i = 0; i < n; i++) {scanf("%d", &nums[i]); // 输入数组}// 对数组进行升序排序qsort(nums, n, sizeof(int), compare);// 求中位数位置：// 如果 n 为奇数，取 nums[n / 2]// 如果 n 为偶数，取 nums[n / 2 - 1]// 上述两种情况统一写作 nums[ceil(n / 2.0) - 1]int medianIndex = (int)ceil(n / 2.0) - 1;int median = nums[medianIndex];printf("%d\n", median);return 0;
}

Node JavaScript

const readline = require('readline');const rl = readline.createInterface({input: process.stdin,output: process.stdout
});let inputLines = [];rl.on('line', line => {inputLines.push(line.trim());
}).on('close', () => {const n = parseInt(inputLines[0]); // 输入点的数量const nums = inputLines[1].split(' ').map(Number); // 输入数组// 对数组进行排序nums.sort((a, b) => a - b);// 统一中位数写法：Math.ceil(n / 2) - 1const median = nums[Math.ceil(n / 2) - 1];console.log(median);
});

Go

package mainimport ("bufio""fmt""os""sort""strconv""strings""math"
)func main() {scanner := bufio.NewScanner(os.Stdin)// 读取点的数量scanner.Scan()n, _ := strconv.Atoi(scanner.Text())// 读取并解析数组scanner.Scan()strs := strings.Fields(scanner.Text())nums := make([]int, n)for i, s := range strs {nums[i], _ = strconv.Atoi(s)}// 排序sort.Ints(nums)// 取中位数（统一写法：ceil(n/2)-1）medianIndex := int(math.Ceil(float64(n)/2.0)) - 1fmt.Println(nums[medianIndex])
}

时空复杂度

时间复杂度：O(nlogn)。排序所需时间复杂度

空间复杂度：O(1)。除了输入的序列且忽略排序所需的编译栈空间，仅需若干常数变量维护遍历过程。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华子OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务1000+同学成功上岸！

• 课程讲师为全网200w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 90+天陪伴式学习，100+直播课时，300+动画图解视频，500+LeetCode经典题，500+华为OD真题/大厂真题，还有简历修改、模拟面试、陪伴小群、资深HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接OD真题汇总(持续更新)

• 绿色聊天软件戳 od1441或了解更多