【三维重建-对极几何】极线约束（Epipolar Constraint）

极线约束（Epipolar Constraint）总结

一、基本定义

极线约束（Epipolar Constraint） 描述了两幅图像中对应点之间的几何关系。

对于两台相机拍摄的同一个三维点 $P$，它在两张图像中的投影 $p$ 与 $p^{\prime }$ 满足以下关系：

$$p^{\prime \mathsf{T}}Fp=0$$

其中，$F$ 是两幅图像之间的 基础矩阵（Fundamental Matrix）。

---

二、几何直观

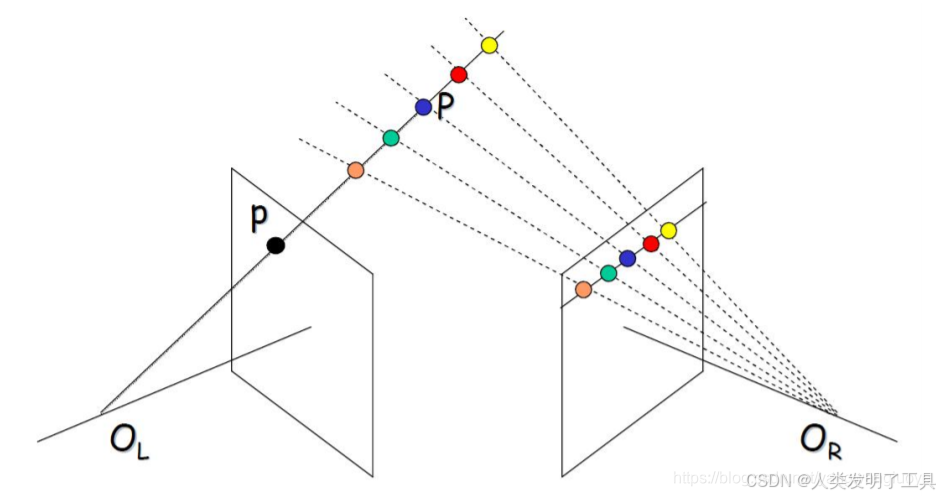
• 两个相机中心 $O_1$ 与 $O_2$ 以及三维点 $P$ 构成一个 极平面（Epipolar Plane）。

• 该平面与两幅图像平面相交，形成两条直线：

  • 左图的极线 $l$
  • 右图的极线 $l^{\prime }$

因此，当一个点 $p$ 在左图中确定后，它在右图中的对应点 $p^{\prime }$ 一定落在对应的极线 $l^{\prime }$ 上。

---

三、核心数学关系

1. 极线方程

$$l^{\prime }=Fp$$

表示：左图中点 $p$ 在右图像中的极线。

2. 点在极线上的条件

若点 $p^{\prime }=[x^{\prime },,y^{\prime },,1{]}^{\mathsf{T}}$ 位于直线 $l^{\prime }=[a,,b,,c{]}^{\mathsf{T}}$ 上，则有：

$$a{x}^{\prime }+b{y}^{\prime }+c=0$$

代入极线方程即可得到：

$$p^{\prime \mathsf{T}}Fp=0$$

这就是极线约束的代数表达式。

---

四、基础矩阵 $F$

基础矩阵 $F\in {\mathbb{R}}^{3\times 3}$ 编码了两幅图像之间的几何关系（旋转和平移）：

$$F=K^{\prime -\mathsf{T}},[t{]}_{\times },R,K^{-1}$$

其中：

• $K,,K^{\prime }$：两相机的内参矩阵
• $R,,t$：相机 2 相对于相机 1 的外参
• $[t{]}_{\times }$：平移向量 $t$ 的反对称矩阵：

$$[t{]}_{\times }=\left[\begin{array}{ccccccc}0& -t_z& t_y{t}_z& 0& -t_x-t_y& t_x& 0\end{array}\right]$$

---

五、几何要素总结

概念	符号	含义
极点	$e,,e^{\prime }$	另一相机光心在当前图像中的投影位置
极线	$l,,l^{\prime }$	极平面与图像平面的交线
极平面	—	由两相机光心与空间点 $P$ 构成的平面
基础矩阵	$F$	将一图像中的点映射为另一图像中的极线
极线约束	$p^{\prime \mathsf{T}}Fp=0$	对应点必须位于极线上

---

六、特殊情况：立体校正（Rectified Stereo）

当两台相机光轴平行、仅沿 $X$ 轴平移时：

• 极线为 水平线
• 匹配搜索可简化为同一行内的水平搜索

这就是 极线校正（Epipolar Rectification） 的几何目的。

---

七、在 MVS / SfM 中的作用

应用场景	作用
SfM（Structure from Motion）	估计基础矩阵，恢复相机姿态
MVS（Multi-View Stereo）	用极线约束限制匹配搜索范围（由二维降为一维）
双目立体匹配（Stereo Matching）	通过极线约束简化代价计算与匹配搜索

---

八、核心意义总结

项目	说明
公式	$p^{\prime \mathsf{T}}Fp=0$
含义	两幅图像的匹配点必须位于同一极平面上
几何本质	三维点、两相机中心共面
代数意义	点 $p^{\prime }$ 在极线 $Fp$ 上
结果	搜索空间由二维降为一维，计算效率显著提升

---

九、直观类比

几何对象	类比
极线方程 $l^{\prime }=Fp$	像“影子”一样投射到另一张图
极线约束 $p^{\prime \mathsf{T}}Fp=0$	表示“点在影子线上”
基础矩阵 $F$	连接两张图像的几何变换关系

---

十、总结一句话

极线约束 = 对应点共面约束。

它让我们不用在整幅图中搜索对应点，只需在一条极线上搜索，
是多视图几何与三维重建的几何基础。