当前位置：首页 > news >正文

树的遍历算法

news 2025/10/10 11:44:12

一、树的遍历概述

二、树的遍历算法

1. 基于 DFS 的先序遍历

2. 基于 DFS 的中序遍历（二叉树）

3. 基于 DFS 的后序遍历

4. 基于 BFS 的层序遍历

三、树的遍历总结

一、树的遍历概述

树（Tree）是一种非常重要的非线性数据结构，它以层次化的形式组织数据，能够清晰地表达元素之间的“包含”或“从属”关系。在树形结构中，节点之间通过“父子”关系连接。为了访问树中每一个节点并进行相应处理，必须遵循一定的访问顺序，这个过程就称为树的遍历（Tree Traversal）。

树的遍历本质上是一种“系统地访问所有节点”的过程，其核心思想是：

在保证不遗漏任一节点的前提下，确定一个访问次序。

根据访问顺序的不同，树的遍历可以分为以下两大类（DFS/BFS本质上将树看成是特殊的图）：

深度优先遍历（Depth-First Search, DFS）
- 沿着树的深层方向尽可能深入节点，直到最深层节点，再回溯到上层未访问的节点。
- 根据访问当前结点次序的不同可划分为三种典型形式：先序遍历（Preorder）、中序遍历（Inorder）、后序遍历（Postorder）。
- 适用于需要完整处理一个子树后再处理兄弟节点的场景，例如表达式树求值。
广度优先遍历（Breadth-First Search, BFS）
- 以层为单位逐层访问节点，从根节点开始，先访问同一层的所有节点，再进入下一层。
- 又称为层序遍历（Level-order Traversal）。
- 适用于需要按层处理节点的场景，如层级展示等。

树的遍历是树算法的基础，它为树的搜索、复制、删除、序列化、构造等操作提供了统一框架。理解遍历方法之间的差异与联系，对于掌握树型数据结构的应用至关重要。

二、树的遍历算法

本节将系统介绍树的常见遍历算法。关于图的 DFS 和 BFS，请参考文章图的遍历，本文重点关注一般树结构的遍历框架。

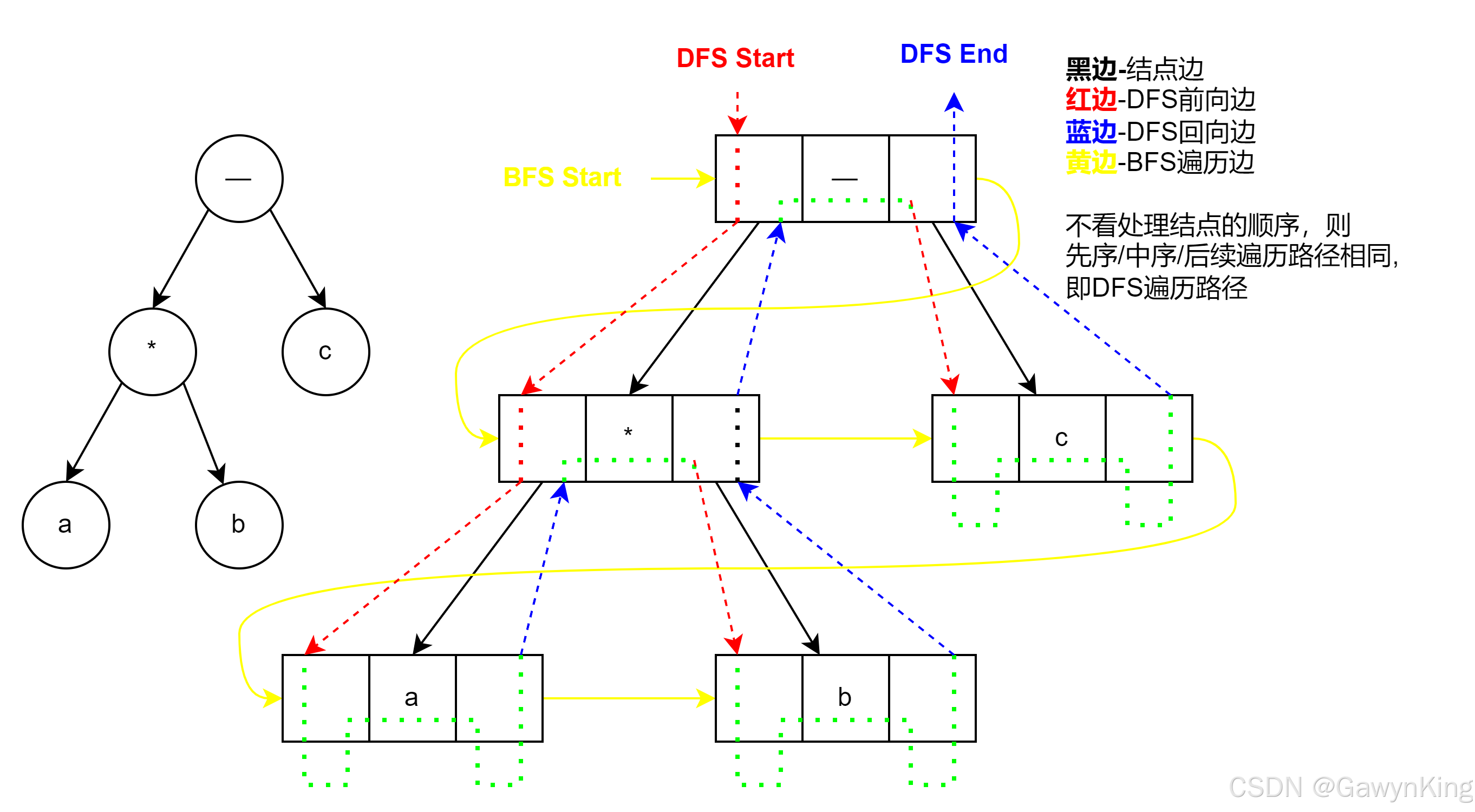
1. 基于 DFS 的先序遍历

在先序遍历中，每个节点的访问顺序为：先访问根节点，再访问其所有子节点。换言之，对于任意节点：

访问该节点；
按顺序对每个子节点递归执行先序遍历。

对于二叉树而言，其访问顺序是“根 → 左子树 → 右子树”；对于一般树，则是“根 → 第一个孩子 → 第二个孩子 → …… → 第 n 个孩子”。

算法思想：

使用递归或显式栈实现；
当访问到某个节点时，立即处理它；
然后依次访问它的所有子节点。

Java代码示例：

package org.algds.tree.traversal;

import org.algds.tree.ds.TreeNode;

import java.util.List;
import java.util.Stack;

/*** 树的先序遍历，扩展到图属于DFS范畴，适用于二叉树或N叉树*/
public class PreOrderTraverse {
/*** 递归先序遍历*/public static <T> void preOrderRecursive(TreeNode<T> root) {if (root == null) {return;}
// 处理当前节点print(root);
// 递归处理所有子节点for (TreeNode<?> child : root.getChildren()) {preOrderRecursive(child);}}

/*** 基于栈的先序遍历*/public static <T> void preOrderStack(TreeNode<T> root) {if (root == null) {return;}
Stack<TreeNode<T>> stack = new Stack<>();stack.push(root);
while (!stack.isEmpty()) {TreeNode<T> current = stack.pop();print(current);
// 将子节点逆序压入栈中，保证从左到右遍历List<TreeNode<T>> children = current.getChildren();for (int i = children.size() - 1; i >= 0; i--) {stack.push(children.get(i));}}}

/*** 访问节点方法，节点打印方法*/private static <T> void print(TreeNode<T> node) {System.out.print(node.getData() + " ");}

/*** 单元测试，构建测试树结构：*         A*        /|\*       B C D*      /|   |*     E F   G*           |*           H*/public static void main(String[] args) {System.out.println("=== 树的孩子表示法 - 先序遍历演示 ===\n");
// 1 构造树节点TreeNode<String> root = new TreeNode<>("A");TreeNode<String> B = new TreeNode<>("B");TreeNode<String> C = new TreeNode<>("C");TreeNode<String> D = new TreeNode<>("D");TreeNode<String> E = new TreeNode<>("E");TreeNode<String> F = new TreeNode<>("F");TreeNode<String> G = new TreeNode<>("G");TreeNode<String> H = new TreeNode<>("H");

// 3 构建树结构root.addChildren(B);root.addChildren(C);root.addChildren(D);
B.addChildren(E);B.addChildren(F);
D.addChildren(G);G.addChildren(H);

// 1 递归先序遍历System.out.println("1. 递归先序遍历结果:");preOrderRecursive(root);System.out.println("\n");
// 2 栈先序遍历System.out.println("2. 基于栈的先序遍历结果:");preOrderStack(root);System.out.println("\n");
System.out.println("=== 演示结束 ===");}

}

2. 基于 DFS 的中序遍历（二叉树）

中序遍历是二叉树特有的遍历方式，其访问顺序为：

左子树 → 根节点 → 右子树

即，对于任意二叉树节点：

递归遍历其左子树；
访问根节点；
递归遍历右子树。

算法思想：

由于中序遍历依赖于“左右”子树的对称结构，因此只能应用于二叉树；
常用递归实现，也可通过栈实现非递归形式；
对于二叉搜索树（BST），中序遍历的结果是一个有序序列。

Java代码示例：

package org.algds.tree.traversal.binary;

import org.algds.tree.ds.BinaryTreeNode;
import java.util.Stack;

/*** 推广到图属于DFS遍历范畴，仅二叉树遍历支持中序遍历*/
public class InOrderTraverse {
/*** 递归中序遍历*/public static void inOrderRecursive(BinaryTreeNode<?> root) {if (root == null) return;
// print(root);                     // 前序访问inOrderRecursive(root.getLeft());   // 遍历左子树print(root);                        // 访问根节点-中序访问inOrderRecursive(root.getRight());  // 遍历右子树// print(root);                     // 后序访问}
/*** 迭代中序遍历（使用栈）*/public static void inOrderIterative(BinaryTreeNode<?> root) {if (root == null) return;
Stack<BinaryTreeNode<?>> stack = new Stack<>();BinaryTreeNode<?> current = root;
while (current != null || !stack.isEmpty()) {// 将左子树的所有节点入栈(向左走到尽头)while (current != null) {stack.push(current);current = current.getLeft();}
// 弹出栈顶节点并访问current = stack.pop();print(current);
// 转向右子树current = current.getRight();}}

/*** Morris中序遍历*/public static <T> void inorderMorris(BinaryTreeNode<T> root) {BinaryTreeNode<T> current = root;
while (current != null) {if (current.getLeft() == null) {// 如果没有左子树，直接访问当前节点print(current);current = current.getRight();} else {// 找到当前节点的前驱节点（左子树的最右节点）BinaryTreeNode<T> predecessor = current.getLeft();while (predecessor.getRight() != null && !predecessor.getRight().equals(current)) {predecessor = predecessor.getRight();}
if (predecessor.getRight() == null) {// 建立临时链接，便于回溯predecessor.setRight(current);current = current.getLeft();} else {// 恢复树的结构并访问节点predecessor.setRight(null);print(current);current = current.getRight();}}}}

/*** 访问节点的方法*/private static void print(BinaryTreeNode<?> node) {System.out.print(node + " ");}
/*** 单元测试*     A*    / \*   B   C*  / \* D   E*/public static void main(String[] args) {
// 字符串类型的二叉树System.out.println("\n=== 字符串类型二叉树测试 ===");BinaryTreeNode<String> root = new BinaryTreeNode<>("A");BinaryTreeNode<String> B = new BinaryTreeNode<>("B");BinaryTreeNode<String> C = new BinaryTreeNode<>("C");BinaryTreeNode<String> D = new BinaryTreeNode<>("D");BinaryTreeNode<String> E = new BinaryTreeNode<>("E");
root.setLeft(B);root.setRight(C);B.setLeft(D);B.setRight(E);

System.out.print("递归中序遍历: ");inOrderRecursive(root);System.out.println("\n");
System.out.print("迭代中序遍历: ");inOrderIterative(root);System.out.println("\n");
System.out.print("Morris中序遍历: ");inorderMorris(root);System.out.println("\n");}
}

3. 基于 DFS 的后序遍历

后序遍历的访问顺序为：

所有子节点 → 根节点

对于任意节点：

递归遍历其所有子节点；
最后访问该节点本身。

对于二叉树而言，即“左子树 → 右子树 → 根节点”。

算法思想：

通过递归或栈实现；
在访问节点前，必须确保所有子节点已被访问；
特别适用于“自底向上”处理的场景，例如节点销毁、资源回收、子结果合并等。

Java代码示例：

package org.algds.tree.traversal;

import org.algds.tree.ds.TreeNode;

import java.util.List;
import java.util.Stack;

/*** 树的后序遍历*/
public class PostOrderTraverse {
/*** 递归后序遍历*/public static <T> void postOrderRecursive(TreeNode<T> root) {if (root == null) {return;}
// 递归处理所有子节点for (TreeNode<?> child : root.getChildren()) {postOrderRecursive(child);}
// 处理当前节点 - 打印print(root);}

/*** 基于栈的后序遍历(双栈遍历)*/public static <T> void postOrderStack(TreeNode<T> root) {if (root == null) {return;}
Stack<TreeNode<T>> stack = new Stack<>();Stack<TreeNode<T>> output = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {TreeNode<T> current = stack.pop();output.push(current);
// 将子节点按顺序压入栈中List<TreeNode<T>> children = current.getChildren();for (TreeNode<T> child : children) {stack.push(child);}}
// 输出栈中的节点（逆序弹出）while (!output.isEmpty()) {print(output.pop());}}

/*** 节点打印方法*/private static <T> void print(TreeNode<T> node) {System.out.print(node.getData() + " ");}
/*** 单元测试，构建测试树结构：*         A*        /|\*       B C D*      /|   |*     E F   G*           |*           H*/public static void main(String[] args) {System.out.println("=== 树的孩子表示法 - 后序遍历演示 ===\n");
// 构造树节点TreeNode<String> root = new TreeNode<>("A");TreeNode<String> B = new TreeNode<>("B");TreeNode<String> C = new TreeNode<>("C");TreeNode<String> D = new TreeNode<>("D");TreeNode<String> E = new TreeNode<>("E");TreeNode<String> F = new TreeNode<>("F");TreeNode<String> G = new TreeNode<>("G");TreeNode<String> H = new TreeNode<>("H");
// 构建树结构root.addChildren(B);root.addChildren(C);root.addChildren(D);
B.addChildren(E);B.addChildren(F);
D.addChildren(G);G.addChildren(H);
// 1 递归后序遍历System.out.println("1. 递归后序遍历结果:");postOrderRecursive(root);System.out.println("\n");
// 2 双栈法后序遍历System.out.println("2. 基于双栈的后序遍历结果:");postOrderStack(root);System.out.println("\n");
System.out.println("=== 演示结束 ===");}
}

后序遍历的实现相对复杂，尤其在非递归形式中，需要借助辅助栈来记录“已访问子节点”的状态。但在逻辑上，它更贴近实际的任务依赖流程。

4. 基于 BFS 的层序遍历

层序遍历是一种典型的广度优先遍历方式，其访问顺序为：

从上到下、从左到右按层访问节点

即：

先访问根节点；
再访问根节点的所有子节点；
然后访问这些子节点的孩子，依次类推，直到所有层都访问完。

算法思想：

借助队列（Queue）实现；
每次从队列中取出一个节点，并将其所有未访问的子节点加入队列尾部；
循环执行直到队列为空。

Java代码示例：

package org.algds.tree.traversal;

import org.algds.tree.ds.TreeNode;

import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

/*** 树的层序遍历算法*/
public class LevelOrderTraverse {
/*** 层序遍历 - 简化版本（只按顺序输出，不显示层级）*/public static <T> void levelOrderTraverse(TreeNode<T> root) {if (root == null) {return;}
Queue<TreeNode<T>> queue = new LinkedList<>();queue.offer(root);
while (!queue.isEmpty()) {TreeNode<T> current = queue.poll();print(current);
// 将当前节点的所有子节点加入队列for (TreeNode<T> child : current.getChildren()) {queue.offer(child);}}
}

/*** 节点打印方法*/private static <T> void print(TreeNode<T> node) {System.out.print(node.getData() + " ");}
/*** 单元测试，构建测试树结构：*         A*        /|\*       B C D*      /|   |*     E F   G*           |*           H*/public static void main(String[] args) {System.out.println("=== 树的孩子表示法 - 层序遍历演示 ===\n");
// 构造树节点TreeNode<String> root = new TreeNode<>("A");TreeNode<String> B = new TreeNode<>("B");TreeNode<String> C = new TreeNode<>("C");TreeNode<String> D = new TreeNode<>("D");TreeNode<String> E = new TreeNode<>("E");TreeNode<String> F = new TreeNode<>("F");TreeNode<String> G = new TreeNode<>("G");TreeNode<String> H = new TreeNode<>("H");
// 构建树结构root.addChildren(B);root.addChildren(C);root.addChildren(D);
B.addChildren(E);B.addChildren(F);
D.addChildren(G);G.addChildren(H);
// 层序遍历System.out.println("1. 层序遍历:");levelOrderTraverse(root);System.out.println("\n");
System.out.println("=== 演示结束 ===");}
}

三、树的遍历总结

树的遍历是树操作的基础。无论是构造树、查找节点、删除子树，还是进行计算、序列化，都离不开遍历操作。不同的遍历策略反映了不同的访问需求。

遍历方式	类别	访问顺序	典型实现	主要应用场景
先序遍历	DFS	根 → 子树	递归/栈	复制结构、序列化、表达式前缀形式
中序遍历	DFS（二叉树）	左 → 根 → 右	递归/栈	二叉搜索树排序、中缀表达式
后序遍历	DFS	子树 → 根	递归/栈	删除树、依赖计算、后缀表达式
层序遍历	BFS	层级顺序	队列	层次输出、最短路径、深度计算