第一章：5.前缀和

用空间替换时间的算法、

1.【模板】前缀和

 

#include<iostream>
using namespace std;
//f[N]为相加，a[i]最大数到10的九次方，有越界的风险
typedef long long LL;
const int N = 1e5 + 10;
int a[N];
LL f[N];
int n, q;

int main()
{
	cin >> n >> q;
	for (int i = 1; i <= n; i++)cin >> a[i];

	for (int i = 1; i <= n; i++)
	{
		f[i] = f[i - 1] + a[i];
	}

	while (q--)
	{
		int l, r; cin >> l >> r;
		cout << f[r] - f[l - 1] << endl;
	}
	return 0;
}

使用暴力解法的话，会超出时间限制 

f[i] 表示前i位的和

核心代码：

for (int i = 1; i <= n; i++)
    {
        f[i] = f[i - 1] + a[i];
    }

2. P1115 最大子段和 - 洛谷

#include<iostream>

using namespace std;

typedef long long LL;

int n;
const int N = 2e5 + 10;
LL a[N];
LL f[N];

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> a[i];

	for (int i = 1; i <= n; i++)
	{
		f[i] = f[i - 1] + a[i];
	}

	LL ret = -1e20;//最终结果
	LL premin = 0;//前i个最小前缀和

	for (int i = 1; i <= n; i++)
	{
		ret = max(ret, f[i] - premin);
		premin = min(premin, f[i]);
	}
	cout << ret << endl;
	return 0;
}

 运用前缀和算出f[i]

用f[i] 减去 【1，i-1】之间的最小值即可

更新下一个位置的premin最小值

3.【模板】二维前缀和

 

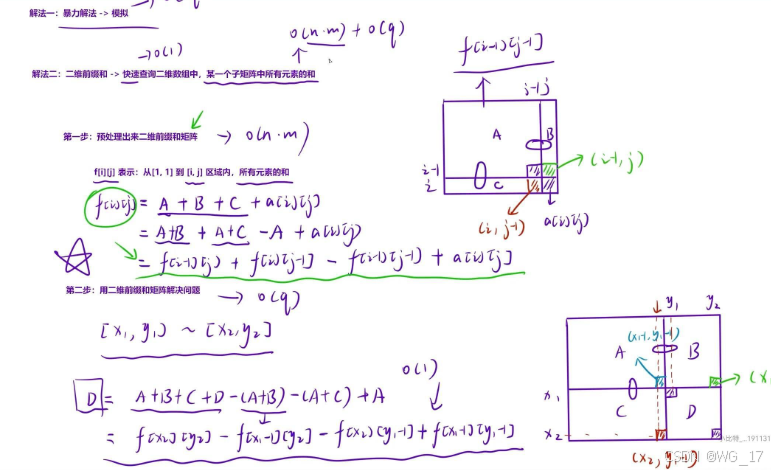
#include<iostream>

using namespace std;

typedef long long LL;

int n, m;
int q;

const int N = 1e3 + 10;

int a[N][N];
LL f[N][N];

int main()
{
	cin >> n >> m >> q;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			cin >> a[i][j];
		}
	}
	//实现二维前缀和
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
		}
	}
	while (q--)
	{
		int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
		LL ret = f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1];
		cout << ret << endl;
	}
	return 0;
}

4.P2280 [HNOI2003] 激光炸弹 - 洛谷

 

 

#include<iostream>

using namespace std;

typedef long long LL;

int n, m;
const int N = 5e3 + 10;
int a[N][N];
int f[N][N];

int main()
{
	cin >> n >> m;
	//输入摧毁目标
	while (n--)
	{
		int x, y, v; cin >> x >> y >> v;
		x++, y++;//由于是从1开始存取数据，所以坐标都要+1
		a[x][y] += v;
	}
	n = 5010;
	//实现二维前缀和
	for (int i = 1; i <= N-1; i++)
	{
		for (int j = 1; j < N; j++)
		{
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
		}
	}
	//枚举法开始轰炸
	int ret = 0;//最终结果
	m = min(m, n);
	//列举每一个正方形，右下，左上
	for (int x2 = m; x2 <= N-1; x2++)
	{
		for (int y2 = m; y2 <= N-1; y2++)
		{
			int x1 = x2 - m + 1, y1 = y2 - m + 1;//左上角的坐标
			
			ret = max(ret, f[x2][y2] - f[x2][y1 - 1] - f[x1 - 1][y2] + f[x1 - 1][y1 - 1]);
		}
	}
	cout << ret << endl;
	return 0;
}