【算法】二分查找(二)查找边界二分



目录
题目介绍
二段性
1.二段搜索
1.1搜索段端点
1.1.1住段的左端点
1.1.2住段的右端点
2.死循环
2.1中点偏向
2.2多余搜索
3.模板
3.1求段左端点:编辑
3.2求段右端点:编辑
4.区别
提交代码
题目介绍
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
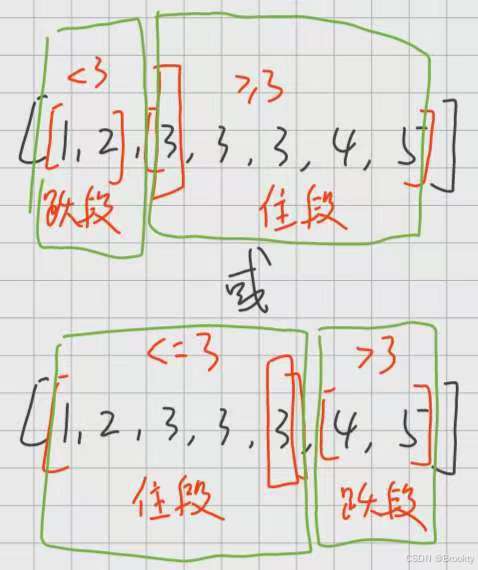
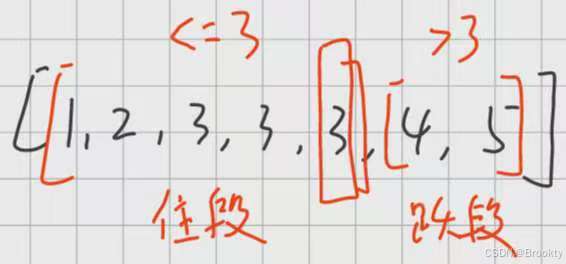
二段性
区域 可划分成 两段部分
1.二段搜索
两指针 在各段部分内 中点算 半缩排区域 地 跃段住段 往界点搜索
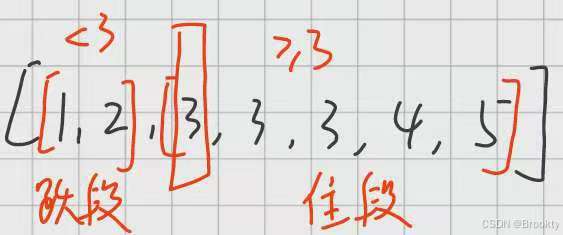
1.1搜索段端点
跃指针与住指针相遇时 算排出 住段部分的端点
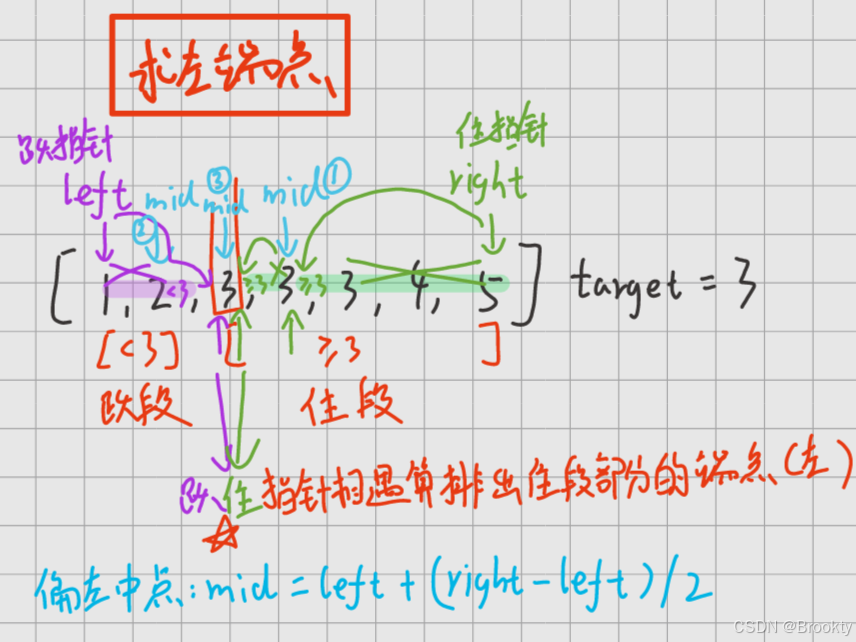
1.1.1住段的左端点
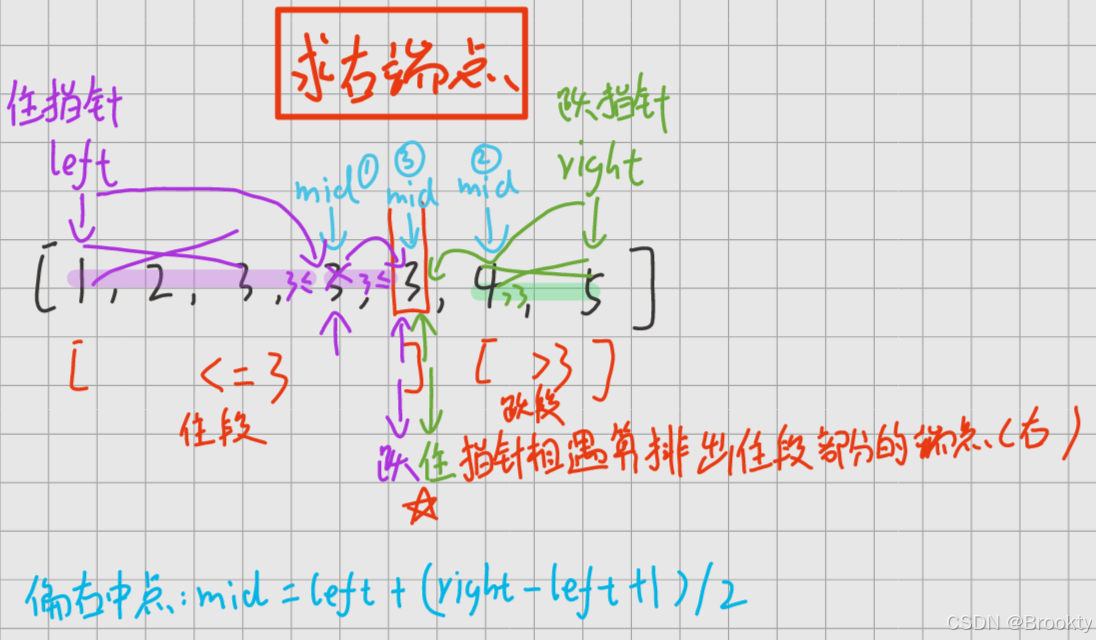
1.1.2住段的右端点
2.死循环
中点 下次立到 在住段部分的 住指针时,住指针的移动 去原地踏步后,再下次的中点也还不变 继续立住指针 去原地踏步,进入死循环
2.1中点偏向
- left + (right - left) / 2 立 偏左中点
- left + (right - left + 1) / 2 立 偏右中点
中点 不能 偏向 住段侧 立,否则 最后中点会立到住指针 而进入死循环
2.2多余搜索
跃指针与住指针相遇 算排得到结果后 就可停止搜索了,如果此时继续去搜索,left == right的中点 会立到住指针 而进入 原地踏步死循环
3.模板
3.1求段左端点:
while(left < right) {
int mid = left + (right - left) / 2; —> 立 偏左中点
if(mid落左跃段) left = mid + 1;
else right = mid; —> mid落右住段
}
3.2求段右端点:
while(left < right) {
int mid = left + (right - left + 1) / 2; —> 立 偏右中点
if(mid落左住段) left = mid;
else right = mid - 1; —> mid落右跃段
}
(最上面 + 1,最下面 - 1)
4.区别
朴素二分 是 找值所在位置 ∈ 边界二分 是 找值范围边界
提交代码
public int[] searchRange(int[] nums, int target) {int[] ret = new int[2];ret[0] = ret[1] = -1;if(nums.length == 0) return ret;// 查找段端点,住段的左端点int left = 0, right = nums.length - 1;while(left < right) { // 不能去多余搜索 left == right时的情况,否则会 中点立到住指针 进入死循环int mid = left + (right - left) / 2; // 中点要偏向跃段部分 即偏左if(nums[mid] < target) left = mid + 1; // mid落左跃段else right = mid; // mid落右住段}if(nums[left] != target) return ret;else ret[0] = left;// 查找段端点,住段的右端点// left = 0; // 接下来左指针 可以直接从找到的左端点处开始 对剩下的右半部分 进行二分 查找右端点right = nums.length - 1;while(left < right) {int mid = left + (right - left + 1) / 2; // 中点不能偏向住段部分 即偏右if(nums[mid] <= target) left = mid; // mid落左住段else right = mid - 1; // mid落右跃段}ret[1] = left;return ret;
}