USCTNET：一种用于物理一致性高光谱图像重建的深度展开核范数优化求解器

摘要​

从单张RGB图像重建高光谱图像（HSI）是一个不适定问题，且在相机光谱灵敏度（CSS）与场景光照参数误设时会导致物理不一致性。本文将RGB至HSI重建定义为基于物理建模的逆问题，通过在可学习的变换域中引入核范数作为正则项，并显式估计CSS与光照以嵌入每次迭代的前向算子，从而确保色度一致性。为规避奇异值阈值法（SVT）所需的全奇异值分解（SVD）的高计算成本与不稳定性，我们提出一种数据自适应的低秩子空间SVT算子。基于此，开发了USCTNet——一种专为HSI设计的深度展开求解器，其将参数估计模块与可学习的近端更新操作耦合。在标准基准上的大量实验表明，该方法在重建精度上持续优于当前最先进的基于RGB的方法。代码：链接 USCTNet-Code-Implementation.git

​索引词— 高光谱图像重建，深度展开网络

1. 引言​

从单张RGB图像 ​X ∈ R​^3×N 中恢复高光谱图像 ​Y ∈ R​^B×N 是一个高度不适定问题，且在未知相机或光照条件下常出现色度不一致性。高光谱图像在波段维度上表现出显著的低秩结构[4]，这促使我们采用核范数正则化作为一种基于物理原理的先验[5]。然而，其近端算子——奇异值阈值法需要重复进行奇异值分解，导致计算量大且在深度训练中梯度不稳定[6]。
为解决这些挑战，我们将RGB至HSI重建表述为一个基于物理建模的逆问题，并开发了USCTNet——一种嵌合成像物理与低秩先验的展开式求解器。令 ​S ∈ R​^3×B 表示相机光谱灵敏度矩阵，​ℓ ∈ R​^B 表示场景光照光谱，则前向模型为：
​X = ΦY, ​Φ = S Diag(ℓ)​​ (1)
（本研究由国家重点研发计划项目（项目编号2023YFD1701001）资助。）
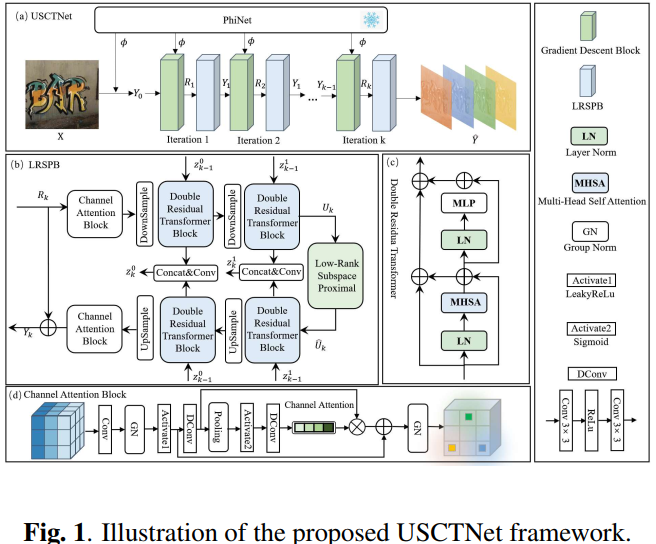
​图1. 提出的USCTNet框架示意图​
USCTNet通过显式估计前向算子 ​Φ​ 来驱动物理引导的梯度更新步骤。在可学习的变换域中，​低秩子空间近端算子​ 通过用学习化的子空间软阈值处理替代全SVD奇异值阈值法，以强制施加核范数先验，从而提升稳定性和效率。
​主要贡献：​​
(1) 提出USCTNet：一种基于物理的展开求解器，将RGB至HSI重建构建为可学习变换域中的核范数正则化逆问题；
(2) 显式估计前向算子 ​Φ​ 并用于驱动数据保真度更新，确保色度一致性，提升跨相机和光照的泛化能力；
(3) 提出LRSP：一种应用于数据驱动子空间的可学习软阈值近端算子，避免全SVD计算并稳定训练过程；
(4) 在标准数据集上，USCTNet在重建精度、感知质量和颜色一致性方面均达到当前最优效果。

2. 相关工作​

​1) 基于RGB的光谱重建​

早期的CNN或Transformer方法通过利用空间-光谱相关性来学习RGB到HSI的映射，并取得了较高的精度[8,13]。然而，由于缺乏显式的物理模型，这些方法在域偏移下常导致色彩伪影和不一致的RGB重建结果[2]。结合相机光谱灵敏度约束的物理一致性模型改善了色彩保真度[3,2]，但这些方法依赖于网络预测的零空间分量，且可能通过伪逆投影放大噪声。此外，现有方法较少利用结构先验。鉴于高光谱图像已被充分证实的低秩特性，核范数正则化成为一种自然的先验选择。

​2) 结合低秩先验的深度展开网络​

深度展开网络将迭代优化算法重构为可学习模块，并利用高效的近端算子[7,16]。近期研究尝试通过变换或扩展表示来展开核范数优化[5,20]，但大多数仍依赖于奇异值分解，这在高光谱图像尺度下计算成本高昂且可能破坏训练稳定性——从而催生了基于子空间感知、无需全SVD的替代方案。

​3) 免全SVD的近端映射​

奇异值阈值法需要重复进行全SVD，对高维高光谱图像计算量巨大。矩阵分解方法通过低秩因子近似核范数[18]；随机子空间投影通过在紧凑基上操作来降低复杂度[17]；而凸凹优化的免SVD迭代仅需主成分计算[21]。这些成果为端到端训练提供了可微分的、可学习的子空间近端映射设计思路。

3. 方法​

​A. 符号与问题设定​
令 ​X ∈ R​^3×N 表示RGB观测图像，​Y ∈ R​^B×N 表示目标高光谱图像（N个像素，B个波段）。前向算子 ​Φ​ 遵循公式(1)。分析-合成变换分别为 ​T_θ : R​^B×N ​→ R​^d×n 和 ​T_θ^† : R​^d×n ​→ R​^B×N，主要沿光谱维度进行操作。d表示变换特征维度，n表示向量化空间尺寸，r ≪ min{d, n} 表示目标子空间秩。
我们通过正则化逆问题恢复Y：
Ŷ = arg min_{Y ∈ R^B×N} ½∥ΦY − X∥_F² + λ∥T_θ(Y)∥_∗ (2)
​B. 展开架构​
​Φ​ 由网络估计并在各阶段共享。步长 η_k > 0 用于稳定梯度更新。分析算子 ​T_θ​​ 转换高光谱图像的域。LRSP(·; τ_k) 表示具有温度调度 τ_k 的可学习低秩子空间近端算子。合成算子 ​T_θ^†​​ 将其转换回原始域。模块 ​M​ 维护记忆状态 ​Z_k​​ 以提供粗略光谱上下文。USCTNet的具体算法流程如下：
​算法1 USCTNet：包含K个展开阶段的前向传播​
​输入：​​ RGB图像X，阶段数K，步长{η_k > 0}，记忆Z₀，初始化Y₀
1:  ​Φ ← PhiNet(X)​​ ▷ 阶段共享的前向算子
2:  ​for​ k = 1, ..., K ​do​
3:    R_k ← Y_k-1 − η_kΦ^⊤(ΦY_k-1 − X) ▷ 物理引导的梯度下降步
4:    U_k ← T_θ(R_k; Z_k-1)
5:    Û_k ← LRSP(U_k; τ_k) ▷ 低秩子空间近端操作
6:    Y_k ← T_θ^†(Û_k)
7:    Z_k ← M(Z_k-1, U_k) ▷ 跨阶段记忆更新
8:  ​end for​
9:  ​return​ Y_K
​C. 低秩子空间近端映射​
我们设计了一个可学习的近端算子来执行子空间奇异值阈值法，以避免全尺寸奇异值分解。在第k阶段，输入为 U_k ∈ R^d×n。r ≪ min{d, n} 是目标秩，T是内部迭代次数，κ是列预算，s是高斯探针数量。以下描述阶段k内的单次内部迭代t。
​​(i) 可微分选择与草图​：通过门控卷积和列池化计算非负重要性 g ∈ (0, 1)ⁿ。通过 f_emb : R^d → R^m 嵌入每列，并用查询向量 q ∈ R^m 评分：
s_i = ⟨f_emb(U_k[:, i]), q⟩,  š_i = (s_i − s_(κ+1))/τ_t, (3)
其中 s_(κ+1) 使用停止梯度，τ_t > 0 是温度参数。软Top-κ权重为：
SoftTop_κ(s; τ_t)_i = softplus(š_i) / Σ_j softplus(š_j). (4)
定义选择器 Ω_t = Diag(g) SoftTop_κ(s; τ_t) ∈ R^n×κ 和标准正交子空间：
Q_t = orth(U_kΩ_t) ∈ R^d×r. (5)
​​(ii) 自适应探测与阈值调度​：使用 Ξ ∼ N(0, 1)^n×s 和 G = Diag(g)Ξ，估计残差比率（作为公式10中的融合权重）：
ρ̃_t = ∥(I − Q_tQ_t^⊤)U_kG∥_F / (∥U_kG∥_F + ε) ∈ (0, 1). (6)
使用轻量级MLP进行细化并预测阈值增量：
(ρ̂_t, Δβ_t) = MLP_η([SparsePool(U_k; Ω_t), ρ̃_t]), (7)
其中 SparsePool(U_k; Ω_t) = Σ_i=1ⁿ Ω_t(i) U_k[:, i] ∈ R^d。
使用指数调度与累积软阈值：
τ_t = max(τ_min, τ₀γ^t-1), β_t+1 = β_t + Δβ_t, β₁ > 0. (8)
​​(iii) 子空间近端与融合​：在迭代t时，将U_k投影到Q_t张成的子空间（公式5）形成紧凑矩阵B_t。随后应用深度可分离模块ConvSVT_ψ(·)作为奇异值收缩的数据自适应替代。其输出通过门控α_t = σ(β_t) ∈ (0, 1)与恒等映射结合，其中β_t为阈值增量（公式8）。最终结果映射回原空间：
B̂_t = (1 − α_t)B_t + α_tConvSVT_ψ(B_t), Û_k,t = Q_tB̂_t. (9)
使用残差感知软权重融合提案：
w_t = exp(−νρ̂_t) / Σ_s=1^T exp(−νρ̂_s), ν > 0, Û_k = Σ_t=1^T w_tÛ_k,t. (10)
​复杂度与可微性​：每内部步骤：子空间草图O(dn)；orth(·)至秩r：O(dr²)；投影O(dnr)；r×n矩阵的薄奇异值分解O(r²n)。总体复杂度O(dnr + r²n)，其中r ≪ n，避免全奇异值分解O(dn min{d, n})。所有组件可微：含τ_t的softplus松弛Top-κ选择，奇异值分解反向传播遵循标准自动微分与软收缩。
​D. 算法网络实现​
采用[1]架构预测前向算子Φ（称为PhiNet）。PhiNet经过预训练，在主网络训练期间保持冻结以避免联合优化不稳定。为防止实验数据泄露，使用与第4节相同的数据集训练分割训练PhiNet。外层分支用[8]的编码器-解码器替代传统分析-合成变换（T_θ–T_θ^†），并针对高光谱数据定制以增强跨波段表示。为进一步提升稳定性，在输入输出端插入卷积引导通道注意力模块（CAB；见图1D），Transformer层配备双残差变换块（DRTB；见图1C）以抑制高维特征梯度振荡。这些模块与LRSP共同构成LRSPB（见图1B）。最后，通过拼接操作与卷积层学习辅助迭代更新项M。主网络采用ℓ₁重建损失进行端到端训练。

4. 实验与结果​

​实施细节​：我们使用PyTorch实现模型。输入归一化至[0,1]并裁剪为128×128图像块（步长为8）。数据增强包括随机翻转与旋转。采用Adam优化器（初始学习率10^-5，β₁=0.9，β₂=0.999）和余弦退火策略训练300轮，批次大小为8。所有实验在NVIDIA A100（40GB）上完成。
​数据集​：在ARAD-1K Real [9]和ICVL [10]上评估USCTNet。由于ICVL缺乏配对RGB图像，我们依据[11]方法合成RGB。移除18张分辨率不一致图像后，得到153个训练样本和30个测试样本。
​定量结果​：采用PSNR、SSIM和SAM指标与当前最优方法对比。如表1所示，USCTNet取得最佳综合精度。
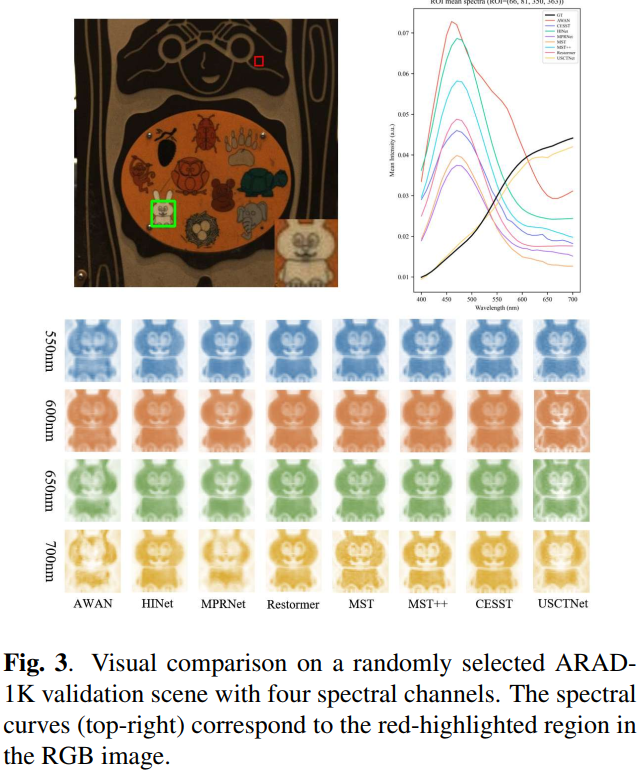
​定性结果​：图2展示了跨波段均方误差图的可视化结果。图3呈现550、600、650及700nm波长的重建效果，USCTNet在保持光谱一致性的同时恢复了更精细的空间细节。图4对比RGB重建效果，同时通过ΔE₀₀指标评估色彩差异一致性。我们的输出与真实值高度吻合，在获得高PSNR/SSIM的同时保持较低ΔE₀₀，表明其具备强物理一致性。
​消融实验​：我们在ARAD-1K Real数据集上评估梯度下降/近端设计（GD+prox）、CAB、DRTB和LRSP的贡献（表2），以MST++为基线。由于全SVD计算成本高、梯度噪声增大及高维奇异值谱数值不稳定，直接集成原始SVT反而降低精度。LRSP通过在低维子空间进行可学习软阈值处理，显式控制有效秩并平滑梯度流，在相同设置下显著提升指标。
表2. 核心模块消融研究（指标对比表格）
我们还对展开迭代次数k进行消融实验：当k<3时模型不收敛，k≥5时过拟合。虽然k=4相比k=3仅带来边际提升却显著增加参数量，最终选择k=3以平衡收敛性、泛化能力与复杂度。

​5. 结论​

本文提出USCTNet——一个基于物理建模的RGB至HSI重建框架，有效协调了光谱精度与RGB保真度。通过两个核心组件整合成像物理与结构先验：（1）显式估计相机光谱灵敏度与光照参数，结合梯度下降数据保真度更新实现色彩一致性重建；（2）低秩子空间近端算子，通过高效子空间SVT施加核范数先验，提升梯度稳定性与可扩展性。该框架通过可学习变换域中的展开求解器实现，在标准基准测试中达到当前最优性能，显著减少RGB-HSI失配误差。通过融合数据驱动建模与物理原理，为遥感与计算摄影领域的可靠光谱重建奠定了理论基础。