当前位置：首页 > news >正文

YOLO入门教程（番外）：YOLOv3创新思想及整体架构

news 2025/10/9 12:53:55

学习资料：《基于深度学习的目标检测原理与应用》
作者：翟中华孙云龙陆澍旸编著

到这里终于把理论暂时告一段落！！！下面终于可以开始实践！！！

Emmm，国庆就结束啦！！！

YOLOv3是目标检测中一个非常经典的算法，在产业界应用很广泛，但是这个算法很复杂，如果一开始就抓细节，那么学习起来会很吃力。

因此我们首先讲解整体框架，然后采用抽丝剥茧的形式逐步讲解。

1 YOLOv3的创新改进

在Pascal Titan X上，YOLOv3能够以30 FPS的速度检测图像，并且在COCO测试开发中的mAP为57.9%。

YOLOv3是在YOLO系列基础上改进而来的，因此，对一些YOLO其他版本的思想有所继承和保留，归结下来有以下3点。

(1)网格思想：从YOLOv1开始，YOLO算法的思想就是将输入划分为多个网格，每个网格输出一定数量的建议框，用来检测目标，只是数量不一样。
(2)端到端思想：利用一个损失函数，一步到位；边框回归和物体分类同时完成。
(3)多尺度思想：多尺度训练可以避免对小物体检测不敏感的情况，但多尺度会降低训练检测速度，这是速度和精度之间的平衡。在R-CNN系列中就有多尺度思想，YOLO继续保持。

对于以上3个优点，YOLOv3将继续保持和发扬光大。YOLOv3如果要改进，则必须从精度和速度方面下功夫。

YOLOv3的创新就是围绕以下4个方面进行的。

(1)Darknet-53。融入“跳过连接”这一深度神经网络经常使用的技巧。
(2)三级检测。分别在32倍、16倍和8倍3个下采样水平进行检测。

例如，输入张量的尺度为416×416，那么下采样后的尺度分别是13×13、26×26、52×52，并且在网络不同阶段做检测，充分利用“神经网络随着层数增加，抽象程度增加，细粒度特征丢失”的规律，因此，可用来检测不同尺度的目标。

浅层特征图（下采样倍数小，如8倍）具有较高的分辨率（52×52），适合检测小目标。
中层特征图（下采样倍数中，如16倍）分辨率中等（26×26），适合检测中目标。
>深层特征图（下采样倍数大，如32倍）分辨率低（13×13），适合检测大目标。

(3)更多锚框。YOLOv2的原始输出尺度是13×13×5，共有845个锚框。YOLOv3借鉴Faster R-CNN系列，每级检测分别设置3个不同宽高比的锚框。锚框数量增加到10647个，比YOLOv2的10倍还多，因此，具有更强的检测能力，但也因此变慢一些。

检测层	特征图尺寸	下采样倍数	锚框数量（该层）	锚框示例（像素）	擅长检测的目标
第1层（小目标）	52 × 52	8倍	52 × 52 × 3 = 8112	(10×13), (16×30), (33×23)	行人、小动物、交通标志等
第2层（中目标）	26 × 26	16倍	26 × 26 × 3 = 2028	(30×61), (62×45), (59×119)	汽车、自行车、人等
第3层（大目标）	13 × 13	32倍	13 × 13 × 3 = 507	(116×90), (156×198), (373×326)	公交车、卡车等大型物体

将这三层的锚框数相加：8112 + 2028 + 507 = 10647个。这相比YOLOv2（13×13×5=845个）增加了十倍以上。

这种设计的核心目的是解决目标检测中目标尺度差异巨大的难题。

浅层特征图（如52×52）：经过的网络层数少，下采样倍数低（8倍），保留的图像细节更多，感受野较小，非常适合捕捉图像中的小目标。
深层特征图（如13×13）：经过多次下采样（32倍），感受野很大，每个点都能“看到”原始图像中很大一片区域，更容易捕捉到大型目标的整体特征。

优势：更多的锚框意味着模型有更多机会去“框住”目标，特别是那些小而密集的物体，这极大地提升了模型的召回率（Recall） 和检测能力，尤其是对小物体的检测效果。

代价：预测每个锚框都需要计算，10647个预测框的计算量远大于YOLOv2的845个，这直接导致了推理速度的下降。YOLOv3的检测速度相比YOLOv2有所降低，正是在精度和速度之间做出的权衡。

(4)修正损失函数。在YOLOv2中，损失函数为均方损失函数，这个损失函数性能一般，因此，YOLOv3使用交叉熵损失函数。YOLOv3通过逻辑回归分别预测目标对象的置信度和类别。

想象一下，你在教一个小朋友认东西。桌上放着一个苹果、一个香蕉和一个橘子。

你的任务就是告诉他：“这个东西是苹果”。

现在，这个小朋友的大脑（就像AI模型）会给出一个猜测，这个猜测是一组信心值，代表它认为这个东西是苹果、香蕉、橘子的可能性有多大。

场景一：用“均方误差（MSE）”老师来教

MSE老师的教学方式：斤斤计较，追求完全一致

小朋友看了一眼说：“我觉得是苹果（信心0.8），香蕉（信心0.1），橘子（信心0.1）”。

正确答案应该是： 苹果（1.0），香蕉（0.0），橘子（0.0）
MSE老师怎么算错误（损失）？
1. 苹果错了：(0.8 - 1.0)² = (-0.2)² = 0.04
2. 香蕉错了：(0.1 - 0.0)² = (0.1)² = 0.01
3. 橘子错了：(0.1 - 0.0)² = (0.1)² = 0.01
- 总错误 = 0.04 + 0.01 + 0.01 = 0.06

MSE老师会说什么？
“不行！你不仅要把对苹果的信心从0.8提高到1.0，你还必须把对香蕉和橘子的信心一丝不差地、准确地降回到绝对的0！差0.1都不行！我要惩罚你！”

它的毛病：
它太“强迫症”了！它要求小朋友所有三个答案都必须和标准答案完全一模一样。小朋友的主要精力浪费在了“如何把香蕉和橘子的信心精准地降为0”这种无关紧要的细节上，而不是专注于“认清这就是个苹果”这个核心任务。

场景二：用“交叉熵（CE）”老师来教

CE老师的教学方式：抓大放小，主次分明

同一个小朋友，同样的回答：“我觉得是苹果（0.8），香蕉（0.1），橘子（0.1）”。

正确答案是： 苹果
CE老师怎么算错误（损失）？
- 它根本不在乎香蕉和橘子具体是多少（是0.1还是0.2，它觉得没区别）。
- 它只盯着一件事：你给正确答案（苹果）的信心是多少？
- 损失计算简化为：-log(苹果的信心) = -log(0.8) ≈ 0.1 （这是一个很小的惩罚，因为0.8已经很高了）

CE老师会说什么？
“很好！你已经知道它是苹果了，信心很高！很棒！接下来你只需要做一件事：继续提高你对‘苹果’的信心，让它无限接近100%（也就是1.0）。至于其他错误选项，你只要让它们变小就行，具体是多小我不强求，别打扰你学主要任务就行。”

它的优点：
非常高效和聪明！它所有的教学（梯度）都集中在强化正确答案上。小朋友所有的精力都用来学习“如何更确定这是苹果”，进步飞快。

为什么YOLOv3要换老师？

因为YOLO要解决的核心任务就是分类（这是苹果还是香蕉？）和判断（这里到底有没有东西？）。

MSE老师：是一个优秀的“数学老师”，适合教预测房价、温度这种要求每个数字都精确的回归问题。但它教分类这种课，方法死板，效率低下。
CE老师：是天生的“分类课老师”，它的教学方法就是为“从多个选项里选一个”这种任务量身定制的，所以教学效率极高，学生（模型）学得又快又好。

所以，YOLOv3把损失函数从MSE换成交叉熵，就像是：
给一个足球培训班，换掉了一个要求球员必须用公式计算射门角度的数学教授，请来了一位只教‘如何把球踢进球门’的职业球星来当教练。后者显然教得更好，球员成绩提升更快！

2 YOLOv3的关键创新点

2.1 106层的Darknet-53主干网络架构

YOLOv2使用了自定义的深度网络架构Darknet-19，在小物体检测上不具优势，这是由于网络在对输入进行下采样时丢失了细粒度特征。

为了解决这个问题，YOLOv2使用了恒等映射，连接来自前一层的特征映射以捕获低级特征。

YOLOv2的架构缺乏一些最重要的元素，这些元素是目前大多数先进算法的主要内容。YOLOv2没有残差块，没有跳过连接，也没有上采样，而这些在YOLOv3中都有。

YOLOv3使用了Darknet的一个变种，它最初有53层网络，并且在ImageNet上训练完成。

对于检测任务，在其上堆叠了53个以上的层，从而为YOLOv3提供了一个106层的全卷积底层架构。这就是YOLOv3比YOLOv2慢的原因。

YOLOv3的整体架构如图7-2-1所示。

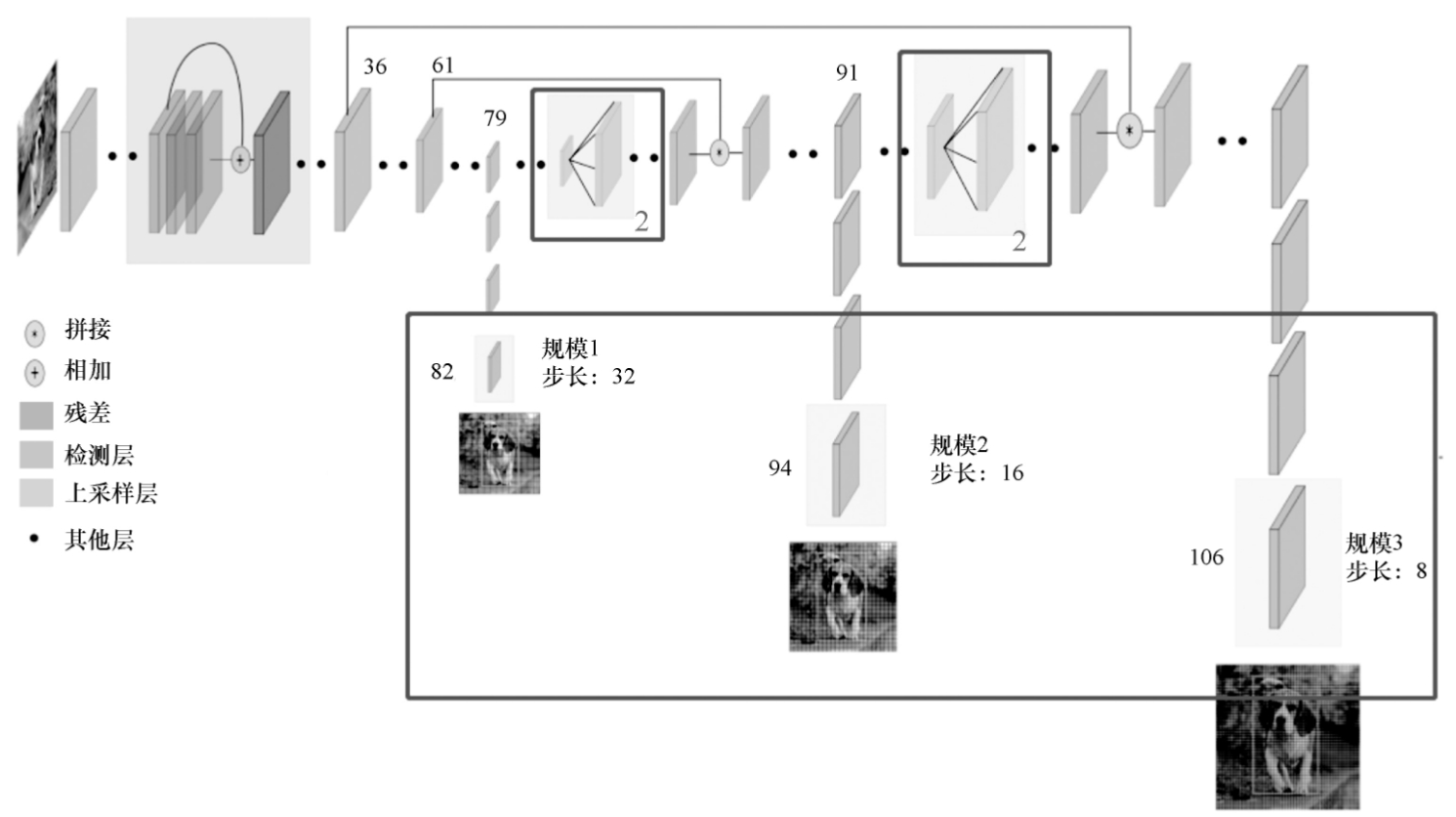
(1)53层包括52个卷积层和1个全连接层。

如图7-2-2所示，左侧的1、2、8、8、4分别是Block（块）的数量；

“Convolutional”表示卷积层；“/2”表示2倍下采样；

“Residual”表示残余连接。

可以看出，每个Block有2个卷积层和1个残余连接。

以下采样为分界，最后是全局平均池化(Avgpool)，之前的所有层可分为6个部分，

开头有1层卷积，其他部分分别是1、2、8、8、4个Block，加上5层下采样卷积，因此，Darknet-53的卷积层数量是(1+2+8+8+4)×2+5+1=52，原论文说有53层卷积是不准确的，加上全连接才有53层。

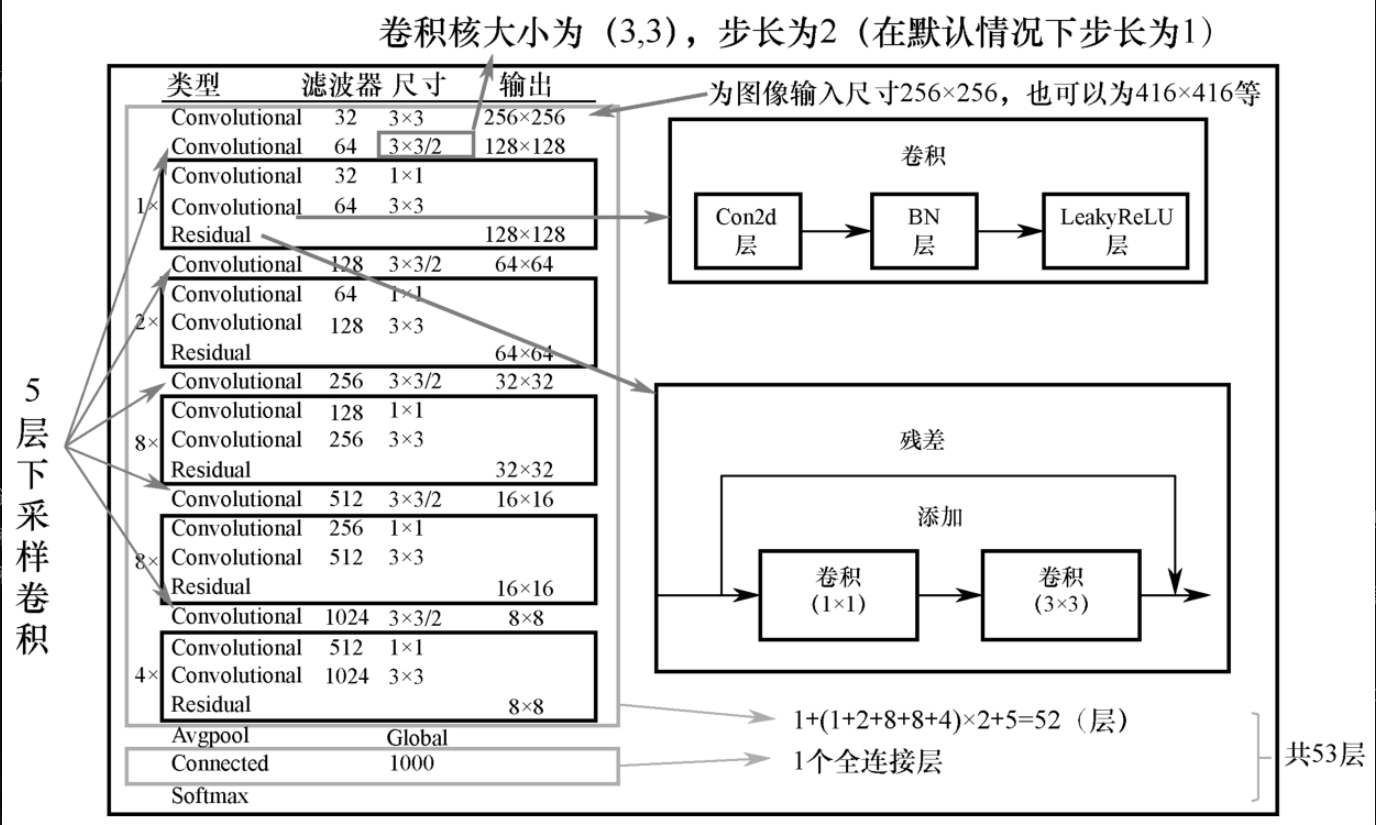
图7-2-2 Darknet-53各层详细结构

进一步看每个Block的内部结构，如图7-2-2所示。

其内部的卷积是由卷积层+BN层+LeakyReLU构成的。

Residual部分包括1×1卷积和3×3卷积。

Residual（残差）

一、核心比喻：抄近道

想象一下你在学一道非常复杂的数学题，解题过程很长，有十几步（这代表一个非常深的神经网络）。

传统网络（没有Residual）：你必须从第一步开始，一步一步地计算到最终答案。如果中间某一步算错了，或者信息丢失了，最终答案就会出错，而且错误很难反向传递回去修正前面的步骤。
Residual 网络（有Residual结构）：它非常聪明！它允许你**“抄近道”。在做完几步复杂的计算后，它会把最开始没算之前的输入**直接拿过来，跳过中间的所有计算步骤，和现在的计算结果相加。

这个“抄近道”的通道，就叫做“残差连接”或“快捷连接”（Shortcut Connection）。
整个这个“抄近道”的结构（包含原来的计算路径和抄近道的路径），就叫做一个“Residual Block”（残差块）。

二、为什么要“抄近道”？它解决了什么问题？

在非常深的网络里，存在两个核心难题：

梯度消失/爆炸（Vanishing/Exploding Gradient）：误差从网络最后面传回到最前面时，信号会变得非常非常弱（消失）或者非常非常强（爆炸），导致网络深层的参数无法被有效更新，前面的层几乎学不到东西。
网络退化（Degradation）：网络层数越深，其性能反而比层数少的网络更差（错误率更高）。这非常反直觉，说明深的网络更难训练，而不是能力不够。

Residual结构如何解决？

解决梯度消失：残差连接提供了一条“高速公路”，让梯度可以直接、无损地从后面流回前面。这样，即使中间卷积层的梯度变得非常小，通过这条“高速公路”回传的梯度依然足够强，确保前面的层能得到有效的训练信号。
解决网络退化：它让网络更容易学习。对于一个Residual Block，它不再需要去学习一个完整的、复杂的映射 H(x)，而是只需要学习输出和输入之间的“残差”或“变化量”F(x)。
- 最终输出 = 原始输入 + 变化量，也就是 Output = x + F(x)
- 如果这个Block发现什么都不做是最好的选择（即恒等映射），它只需要简单地将 F(x) 的学习结果变成 0 就行了。这样 Output = x + 0 = x，信息原封不动地传递下去。
- 这比让一个普通的Block去学习 Output = x（即恒等映射）要容易得多。

简单总结：Residual结构让超深的网络变得可能且容易训练，是深度学习领域一个里程碑式的创新。

三、在YOLOv3的Block里，它是怎么工作的？

图7-2-2中的结构，一个典型的Residual Block工作流程如下：

输入（Input）：一个特征图（比如叫 x）。
主路（Main Path）：
- 先通过一个 1×1 卷积：主要作用是降维，减少通道数，降低计算量。
- 再通过一个 3×3 卷积：主要作用是特征提取，在更低的计算成本下学习特征。
- （中间通常会加入BN层和LeakyReLU激活函数）
- 这一整条主路学习到的，就是上面说的“变化量” F(x)。
短路（Shortcut Path）：输入 x 直接绕开主路，不做任何处理（或者只做简单的线性处理如1x1卷积来调整维度）。
相加（Add）：将主路的输出 F(x) 和短路的输入 x 逐元素相加。
输出（Output）：Output = F(x) + x。
最终激活：相加后的结果通常会再通过一个激活函数（如LeakyReLU）。

（这是一个简化的示意图，帮助理解信息流动）

总结

Residual（残差）：指的是一种网络设计思想，即让网络层去学习“输出相对于输入的变化量”，而不是直接学习完整的输出。
Residual Block（残差块）：是实现上述思想的具体结构，其核心是快捷连接（Shortcut Connection） 和逐元素相加（Add Operation）。
在YOLOv3中的作用：Darknet-53 backbone中大量使用了这种结构，使得YOLOv3的网络可以做得非常深（53层），从而能够从图像中提取更丰富、更抽象的特征，极大地提升了检测精度，尤其是对小物体的检测能力。

(2)106层整体架构包括卷积层、跳过连接层、路由层、上采样层及检测层。

在表7-2-1中有几个关键数字：36层为跳过连接，61层为跳过连接，79层开始为检测层，82层为检测输出。

同理，91层开始为检测层，94层为检测输出；103层开始为检测层、106层为检测输出。

36层是第一个跳过连接，与8倍下采样像素的特征连接以进行检测，因此36层对应的是8倍下采样后的层（第3次下采样层），即第1次卷积+下采样+1×Block+下采样+2×Block+下采样+8×Block。

每个Block有3层网络（注意，这里与前面计算卷积层的方法不同，这里包含Residual层，也算作1层），于是得到1+3+(1+2+8)×3=37，但是网络层序号是从0开始的，于是对应36层。

61层、79层、91层、94层、106层同理。106层YOLOv3详细架构如表7-2-1所示。

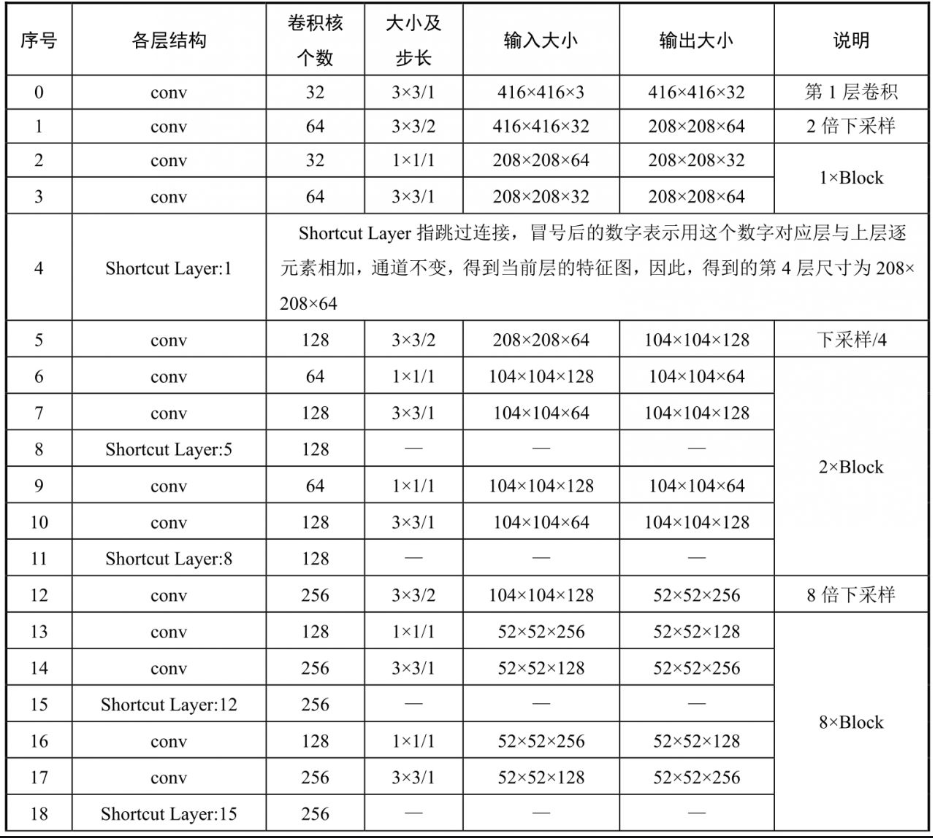
表7-2-1 106层YOLOv3详细架构
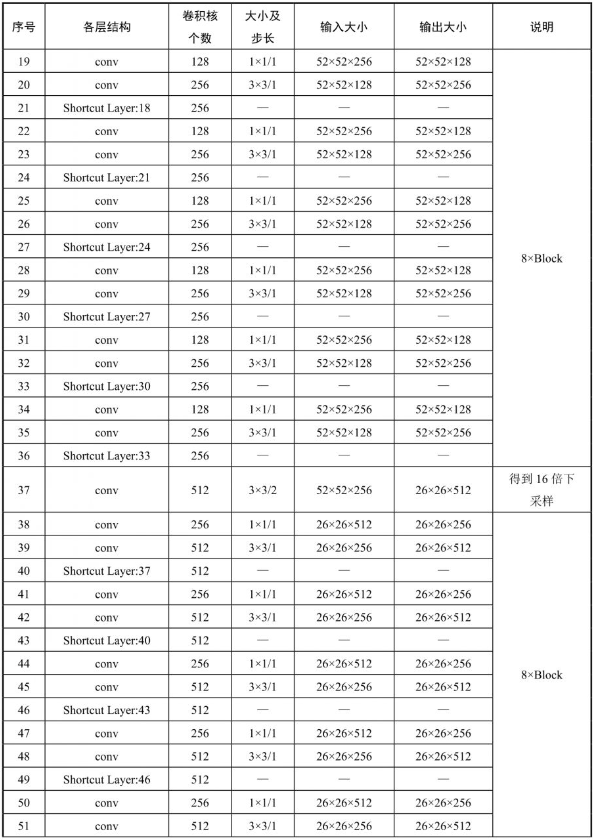
在这里插入图片描述

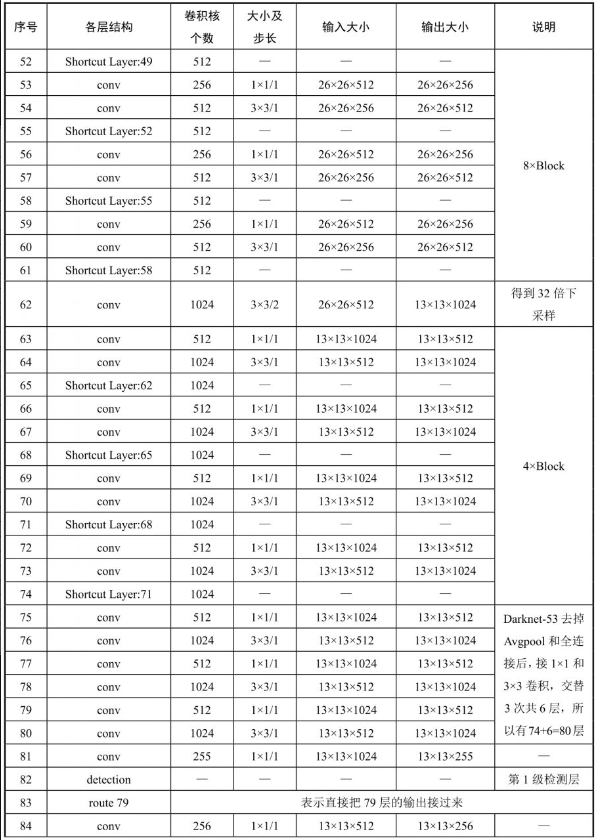
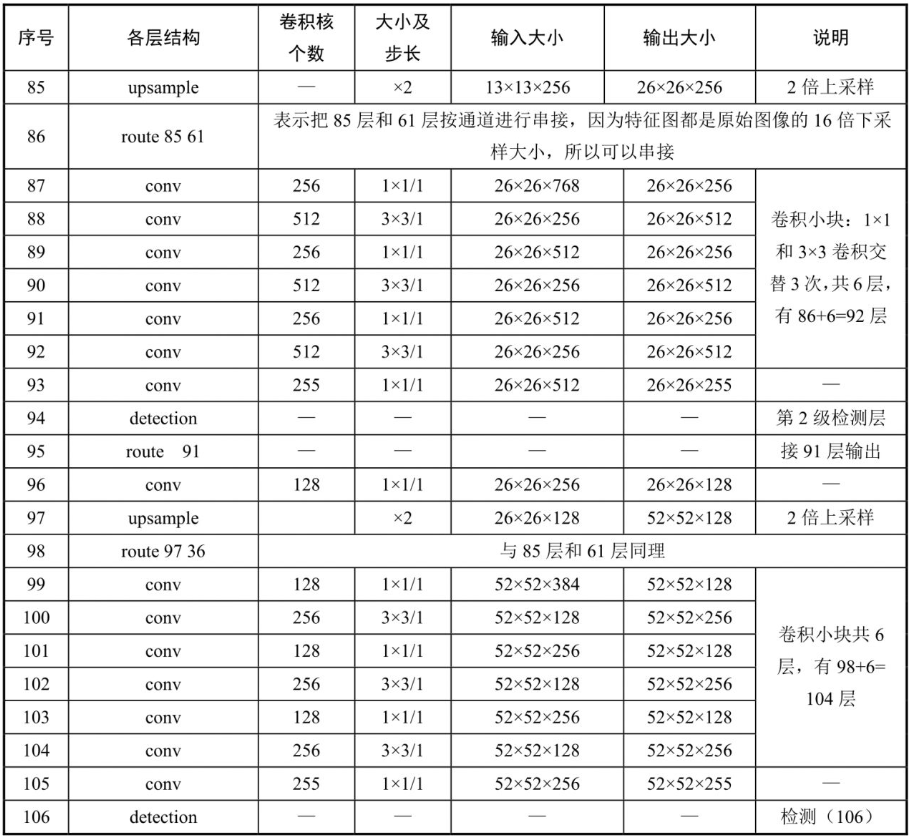
因为层数从0开始，所以共107层。卷积层共75层。利用表7-2-1，再对比整体架构就非常清楚了。

83层由79层直接过来操作，是route 79，这种操作层称为路由层。“74层到80层”“86层到92层”“98层到104层”经过一系列的卷积，称为卷积小块：1×1和3×3卷积交替3次共6层，对应Convolutional Set 5层卷积和后面的3×3卷积，以上就是YOLOv3的整体架构。

2.2 三级检测

YOLOv3最显著的特点是在3个不同的尺度上进行检测。

YOLO是一个全卷积网络，它的最终输出是通过在特征图上应用1×1卷积核来生成的。

在YOLO v3中，检测是通过在网络中3个不同位置的3种不同大小的特征图上应用1×1检测核来完成的。

卷积时设置大于1的步长，就是下采样卷积，步长可表示一个层对输入进行下采样的比率。在以下示例中，假设有一个大小为416×416的输入图像。

YOLOv3在3个尺度上进行预测，这些尺度是通过将输入图像的维度分别下采样32、16和8来精确给出的。

第一个检测是由第82层进行的。

对于前81层，网络对图像进行下采样，因此，81层的倍率为32。如果有416×416的图像，则生成的特征图的大小将是13×13。最后提供13×13×255的用于检测的特征图。

第83层接过第79层特征，然后经过1×1卷积和上采样层，被2倍上采样到26×26的维度，得到第85层，与来自第61层26×26的特征图进行串接，得到第86层，通道数为两者之和。

第86层经过卷积小块，共6层卷积，得到第92层，经过1×1卷积层，得到第93层26×26×255的检测特征图，第94层进行检测。

第95层接过第91层特征，然后经过1×1卷积和上采样层，得到第97层，与来自第36层的特征图进行串接，得到第98层。第98层经过卷积小块，共6层卷积，得到第104层，经过1×1卷积层，得到第105层52×52×255的检测特征图，第106层进行检测。

以上就是106层整个清晰的3级检测架构。

2.3 更擅长检测较小的物体

不同层的检测有助于解决检测小物体的问题。上采样层与前一层（采样前）的连接有助于保留更擅长检测小物体的细粒度特征。

13×13层负责检测大物体，而52×52层检测小物体，26×26层检测中物体。下面是不同层对于同一物体得到不同尺寸特征图的对比分析。

2.4 更多的锚框

对于3级检测，YOLOv3为每种尺度设定3种先验框，对真值框进行聚类，得到9种尺寸的先验框，这9种锚框几乎涵盖了所有可能的锚框。

然后，按照一个尺寸的降序排列锚框。为第一个尺寸分配3个最大的框，为第二个分配接下来的3个，为第三个分配最后3个。也就是每个单元格使用9个锚框。

➢ 大物体：(116×90)(156×198)(373×326)。
➢ 中物体：(30×61)(62×45)(59×119)。
➢ 小物体：(10×13)(16×30)(33×23)。

对于相同大小的输入图像，YOLOv3比YOLOv2预测更多的边界框。例如，在416×416的原始分辨率下，YOLOv2预测了13×13×5=845个框，在每个网格单元中预测5个框。

YOLOv3预测3个不同尺度的框。对于416×416的相同图像，预测框的数量为10647个。可知为什么YOLOv3比YOLOv2慢。

2.5 损失函数

YOLOv2中的最后3项是平方误差，而在YOLOv3中，它们已被交叉熵误差项取代，交叉熵损失效果要比均方损失好得多，因为使用概率对类别进行预测。

YOLOv3损失函数和YOLO、YOLOv2是一脉相承的，如式(7-1)所示。仅在一些地方进行了改进，整个式子仍然分为位置损失、置信度损失和分类损失。

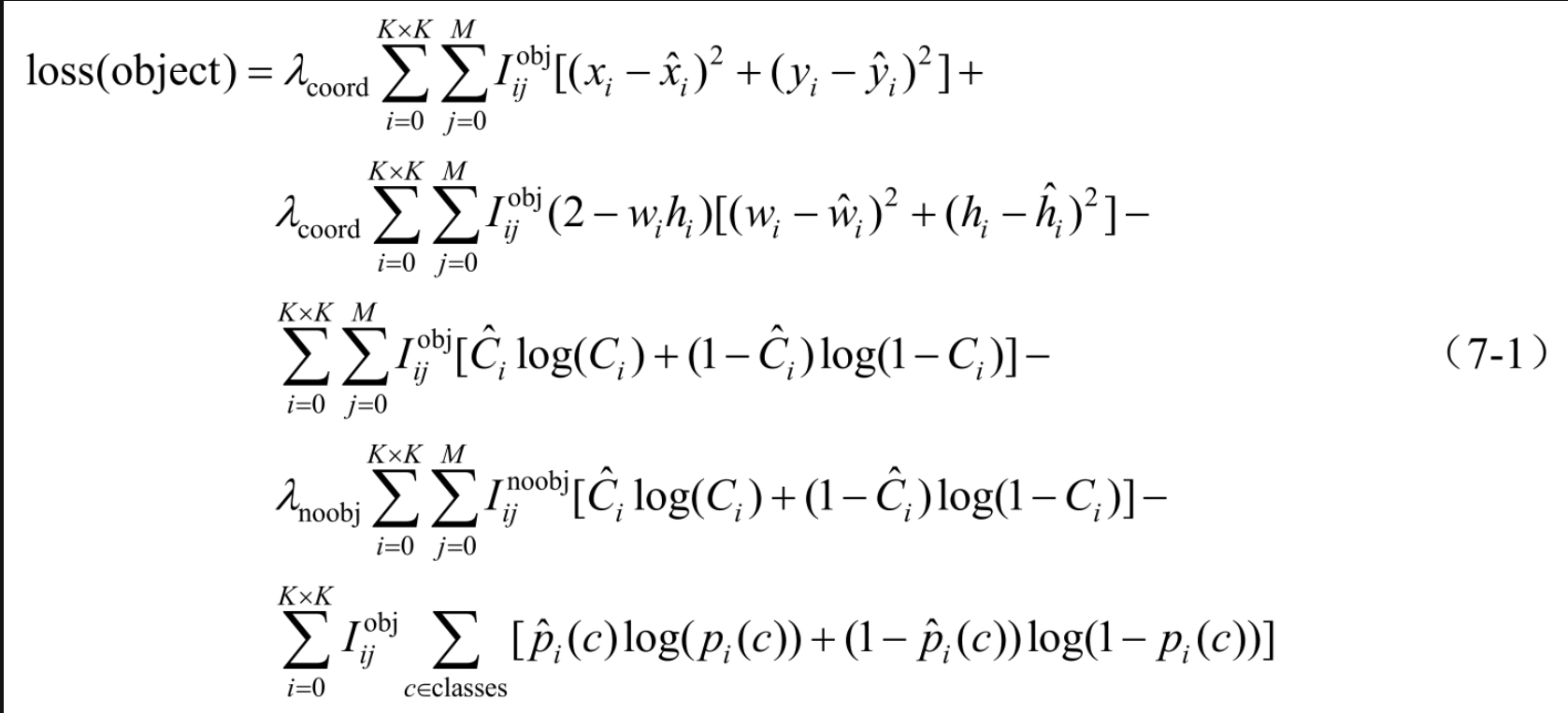
对于位置损失中的宽高损失，这里不再使用平方根，而是使用差值的平方。

同时，加了一个系数2-wh，对于小框，系数略大，对于大框，系数略小，这是为平衡大小框因为框尺寸大小带来的差异。因为宽和高都是相对坐标，所以，相乘以后是小于1的，可以被2减。

对于置信度损失，没有使用平方误差，而是使用交叉熵损失函数。

对于分类损失，同样，使用了交叉熵损失函数。

为什么使用交叉熵损失？因为这样，YOLOv3可以对图像中检测到的对象实现多标签分类。

在YOLOv1、YOLOv2中，作者习惯对类分数进行Softmax计算，并将得分最高的类作为边界框中包含的对象的类。

然而，Softmax基于类是互斥的假设，或者说，如果一个对象属于一个类，那么它就不能属于另一个类，这在COCO数据集中运行良好。

当在数据集中有像person和women这样的类时，上述假设就不成立了。这就是YOLOv3的作者避免对类进行Softmax计算的原因。

相反，使用概率（类逻辑回归方式）预测每个类别的分数，并使用阈值来预测对象的多个标签，分数高于此阈值的类被分配给框，可实现多标签预测。

YOLOv3 损失函数详解表

YOLOv3 的总体损失函数可以看作是 位置预测损失、置信度预测损失和分类预测损失 三大部分的加权和。其核心思想是：使用交叉熵损失取代均方误差来处理概率（分类和置信度）问题，并对位置损失中的宽高预测进行特殊处理以平衡不同大小的目标。

损失组成部分	计算方式 (公式)	改进细节与目的	原因与效果
1. 位置损失 (BBox Loss) 负责预测边界框的中心坐标和宽高	`λ<sub>coord</sub> * Σ[ (2 - wᵢ * hᵢ) * ( (xᵢ - x̂ᵢ)² + (yᵢ - ŷᵢ)² ) ]` `+ λ<sub>coord</sub> * Σ[ (2 - wᵢ * hᵢ) * ( (√wᵢ - √ŵᵢ)² + (√hᵢ - √ĥᵢ)² ) ]`	1. 宽高损失不再取平方根，而是直接使用平方差。 2. 引入了一个*尺度权重系数 `(2 - wᵢ hᵢ)`**。	原因： 1. 平方根操作在早期YOLO中是为了缓和大小框的损失差异，但效果不理想。 2. `wᵢ` 和 `hᵢ` 是归一化后的值（0~1），`(2 - wᵢ * hᵢ)` 的值域为（1~2）。小框的该系数更大，大框的系数更小。效果：平衡大小目标的损失贡献。让模型在训练时更加关注小目标的定位精度，缓解目标检测中“大目标主导梯度”的问题，提升对小目标的检测能力。
2. 置信度损失 (Confidence Loss) 负责判断框内是否有物体 (Objectness)	`-Σ[ Cᵢ * log(Ĉᵢ) + (1 - Cᵢ) * log(1 - Ĉᵢ) ]` （其中，`Cᵢ=1` 为正样本，`Cᵢ=0` 为负样本）	从 YOLOv2 的均方误差 (MSE) 改为二元交叉熵损失 (Binary Cross-Entropy)。	原因：置信度预测本质上是一个二分类问题（有物体/无物体），交叉熵损失是处理概率和二分类问题的最佳选择。它比MSE的梯度更合理，训练更稳定，收敛更快。效果：模型对“是否有物体”的判断更加准确和自信，显著降低了背景误检（False Positive）。
3. 分类损失 (Classification Loss) 负责判断框内物体的具体类别	`-Σ[ Pᵢ(c) * log(Ｐ̂ᵢ(c)) ]` （对每个类别独立使用二元交叉熵）	1. 从 Softmax + MSE 改为独立的二元交叉熵损失。 2. 不再使用 Softmax 将类别分数压缩为单一概率分布。	原因： Softmax 假设类别是互斥的（一个物体只能是“狗”，不能同时是“动物”和“宠物”）。这在COCO等数据集上没问题，但无法进行多标签分类。效果：实现了多标签物体检测。例如，一个边界框可以同时被预测为“人”（类别1）和“女性”（类别2），只要它们的预测概率都超过设定的阈值。这大大增强了模型的实用性。

核心概念对比：为什么是交叉熵？

为了更清晰地理解核心改进，这里有一个对比表格：

特性	YOLOv2 (Softmax + MSE)	YOLOv3 (Sigmoid + BCE)	优势
分类方式	单一标签分类	多标签分类	更符合现实世界，如一个物体可同时是“车”和“救护车”
概率计算	Softmax：所有类别概率之和为1	Sigmoid：每个类别独立计算概率	类别间不再相互竞争，一个框可以属于多个类
损失函数	均方误差 (MSE)	二元交叉熵 (BCE)	BCE是概率预测的天然选择，梯度更优，训练效率更高

总结

通过这个表格，我们可以清晰地看到 YOLOv3 损失函数的精妙之处：

位置预测：通过巧妙的系数设计，增强了对小目标的检测能力。
置信度预测：使用更适合二分类任务的交叉熵损失，提升了判断物体有无的准确性。
分类预测：最大的革新！通过抛弃 Softmax 并采用独立的 Sigmoid 交叉熵损失，一举实现了多标签分类，让模型的能力迈上了一个新台阶。

这些改进使得 YOLOv3 不仅在速度上，更在精度和功能上成为了一个非常强大且实用的目标检测模型。

3 YOLOv3的三级检测输出过程

前面介绍过YOLOv3的整体架构和锚框回归，有整体架构之后，有锚框回归方法，通过输入张量，输出数据，输出数据再通过误差损失函数反向传播，就可以训练模型。

因此，本节讲解的YOLOv3的检测输出过程是非常重要的，要着重理解YOLO是怎样把锚框转成向量的。

前文已经讲过YOLOv3是三级检测机制，通过下采样的3个级别引出3个尺度的检测，分别是32倍、16倍和8倍下采样，倍数越大，像素越低。最大像素为52×52，最小像素为13×13。

用于卷积的检测核的形状为1×1×[B×(5+C)]。这里B是特征图上一个单元格可以预测的边界框数量，“5”代表4个边界框属性和一个对象置信度，C是类的数量。

在COCO上训练的YOLOv3中，B=3和C=80，因此，卷积核大小为1×1×255。此卷积核生成的特征图与之前的特征图具有相同的宽度和高度。

如图7-3-1所示，每级输出都是A×A×3×(4+1+80)，A是每级输出特征图尺寸，分别是13、26和52。

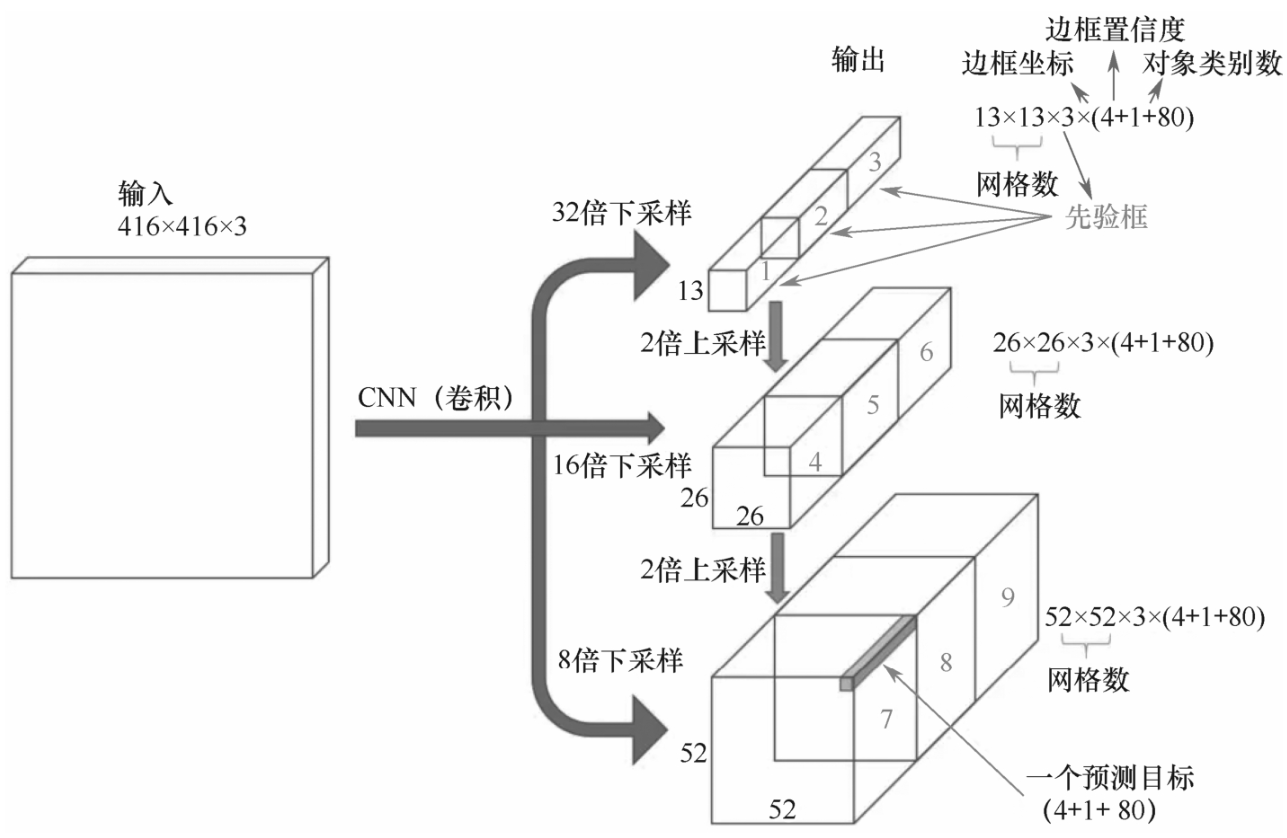
使用图7-3-2来形象说明一下，其中，白色框为真值框，灰色框负责预测白色框的中心和尺寸。

我们的目标就是尽可能达到在灰色框内预测的中心位置接近白色框中心位置，尺度也接近白色物体框。

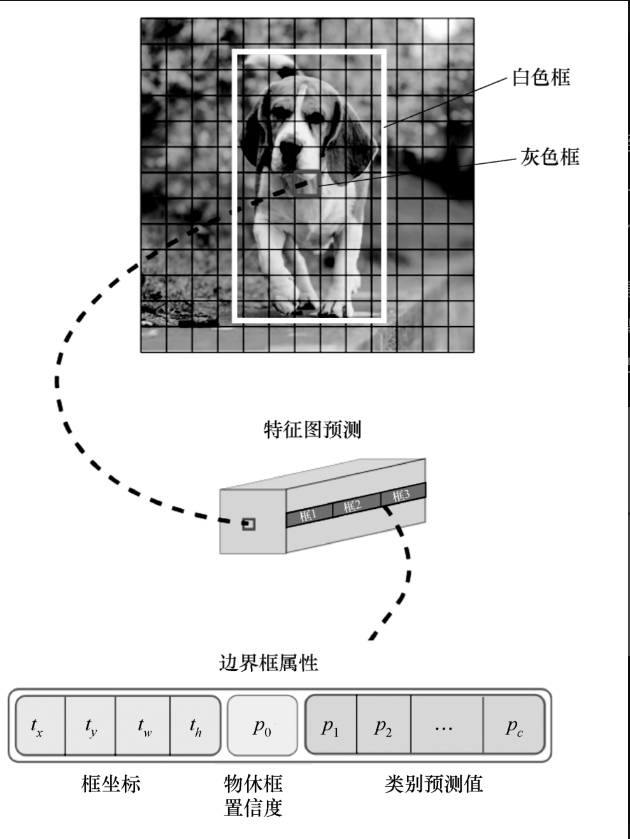
图7-3-2 实例说明YOLOv3

具体做法如下：由灰色框得到3个尺度的锚框（聚类得来的预定义锚框），然后对于每个框，得到4个框的坐标参数(tx、ty、tw、th)、物体框置信度p0、类别预测值p1～pc和框数B。

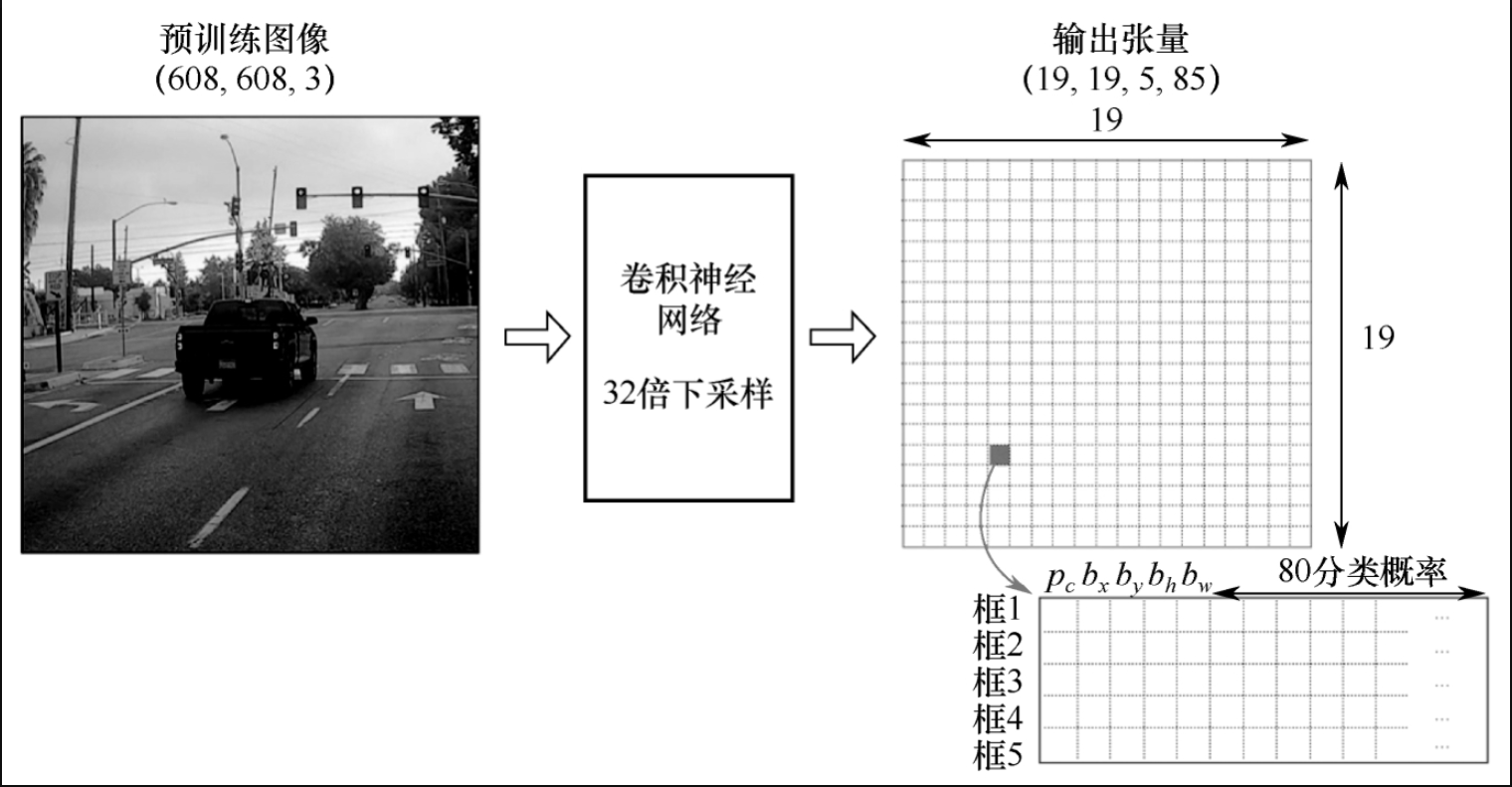
假设在80个分类目标的数据集上有608×608×3的图像，经过卷积神经网络32倍下采样，设置框为5，得到19×19×5×85的张量。

对于下采样后的特征，每个像素都会得到行为5、列为85的张量，如图7-3-3所示。

图7-3-3 举例说明张量计算

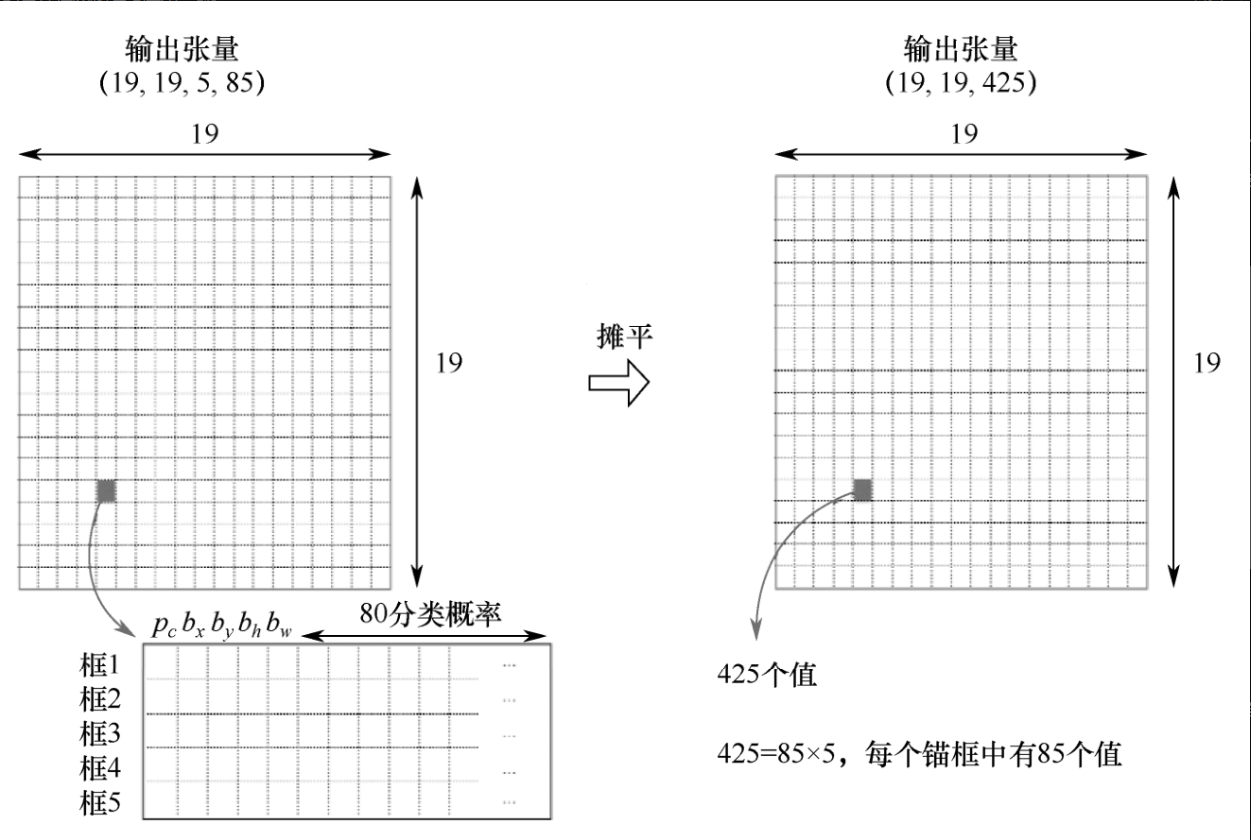
如图7-3-4所示，将19×19×5×85摊平，即把维度重塑为19×19×425，因此，对每个单元格，预测425个值。

有输出数据后，再进一步找概率最大的类别作为边框内物体分类。使用置信度乘以分类分数，就得到该单元格预测的物体。每个单元格都有对应的预测物体。

图7-3-4 摊平张量

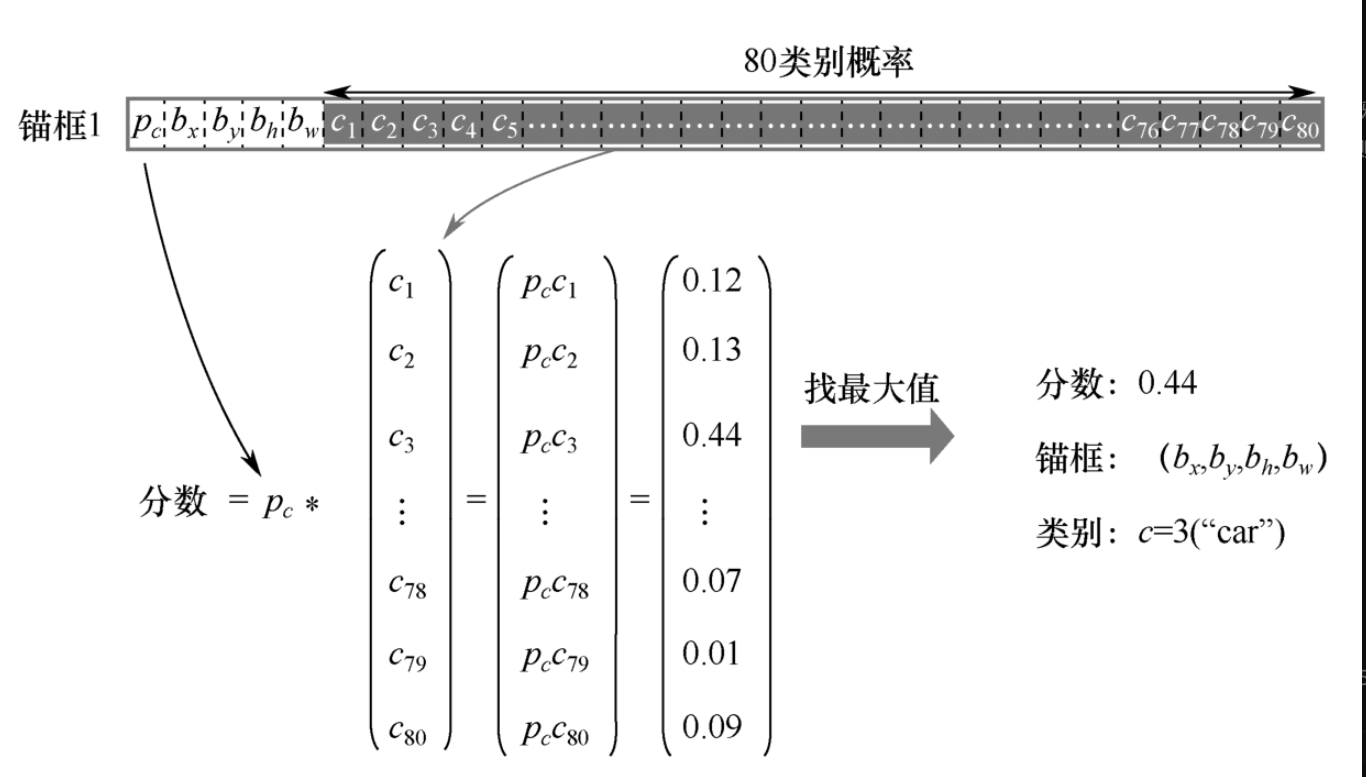
对于每个单元格的每个框，我们将计算点积，提取该框包含每个类的概率，如图7-3-5所示，框(bx，by，bh，bw)以0.44的分数（概率）检测到汽车。

图7-3-5 提取概率

这是一种可视化YOLO在图像上预测的方法。

对于19×19网格，共有361个单元格，对于每个单元格，找到该单元格5个锚框在不同类别的概率得分中的最大值。根据网格单元认为最可能的对象为网格单元着色，执行此操作将得到如图7-3-6所示的图像。

图7-3-6 按最大概率着色

图7-3-6所示的可视化并不是YOLO算法本身进行预测的核心部分，这只是可视化算法中间结果的一种好方法。

可视化YOLO输出的另一种方法是绘制其输出的边界框，这样做将产生图7-3-7所示的可视化效果。

图7-3-7 检测过程中的高概率框
在图7-3-7中，仅绘制了模型已分配高概率的框，但是框仍然太多。我们希望将算法的输出框进一步过滤，保留更有意义的框，可以使用非极大值抑制实现最佳框的筛选。

4 YOLOv3的非极大值抑制

在讲非极大值抑制(NMS)之前，我们来看为什么要使用非极大值抑制。

首先来看一个数字10647，对于一幅图像，如图7-4-1所示，YOLOv3有10647个边框需要检测。

图7-4-1 利用非极大值抑制消除冗余框

这个数字是这样来的，3个尺度，对每个尺度进行3级检测：

3×(13×13+26×26+52×52)=3×(169+4×169+16×169)=63×169=10647

图像中只有少量目标，因此，需要使用非极大值抑制。

具体步骤在之前讲过共经过4个步骤就消除了冗余的低概率框，得到框住各物体的概率最大的检测框。

5 YOLOv3的检测效果

以电影《战狼》中的某个场景为例，如图7-5-1所示，可以看出对于很小的人物目标都能检测出来。

在图7-5-2中，只需一只手就可以检测出有0.52的概率是人；这里将手表检测成钟，虽然错误，但还算比较接近。在图7-5-3中，手枪检测错误，这是因为数据集中没有手枪，不过依然能定位到该物体。

图7-5-1 检测图像中重叠的、较小的人物目标

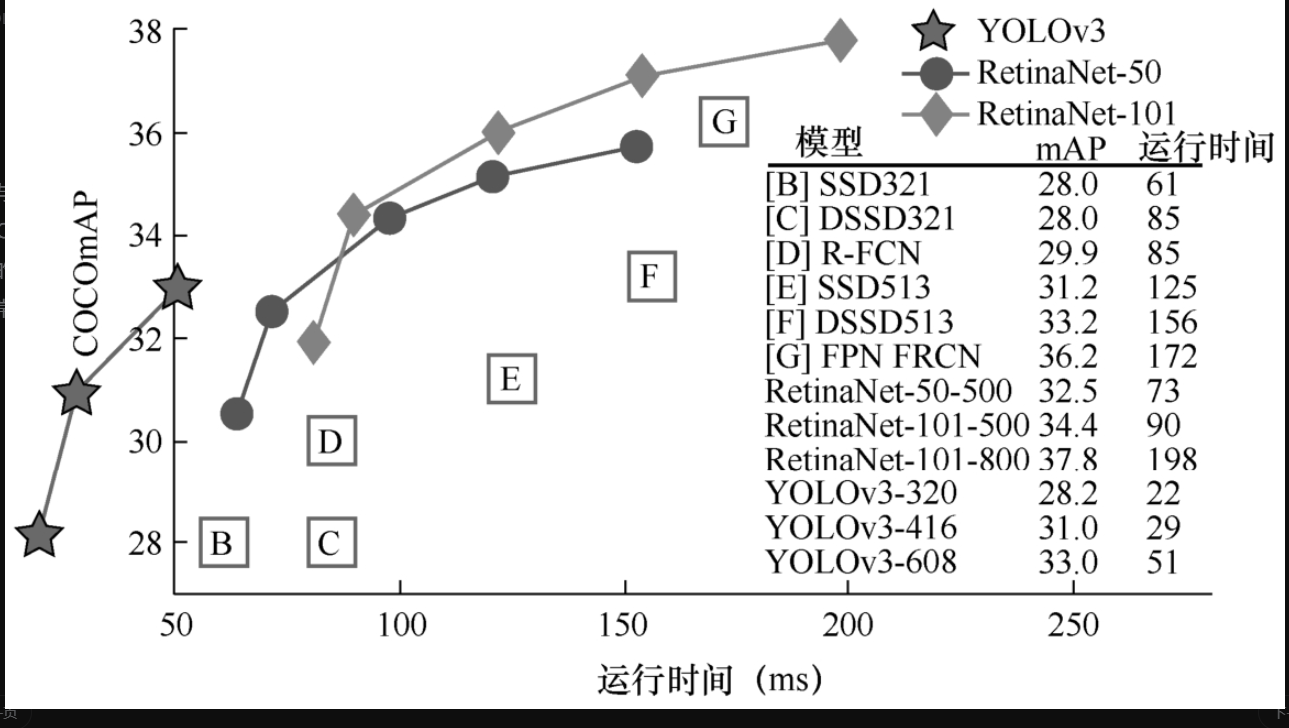
再看与其他算法的效果对比，如图7-5-4所示，与一些主流算法比较，在COCO数据集上的表现，不仅mAP“独占鳌头”，速度也是“一骑绝尘”的。

凭借准确率和速度两个方面的出色表现，YOLOv3成为产业界应用非常广泛的目标检测算法之一。

6 SSD多尺度特征图目标检测思想

前面的章节深入细致地剖析了两阶段检测方法和一阶段检测方法，它们的代表就是R-CNN系列和YOLO系列。

SSD单发多框检测也是一阶段检测方法，因为SSD在实际中有着很广泛的应用，所以，单独用一些篇幅来讲解它。在YOLO的基础上理解SSD是非常容易的。

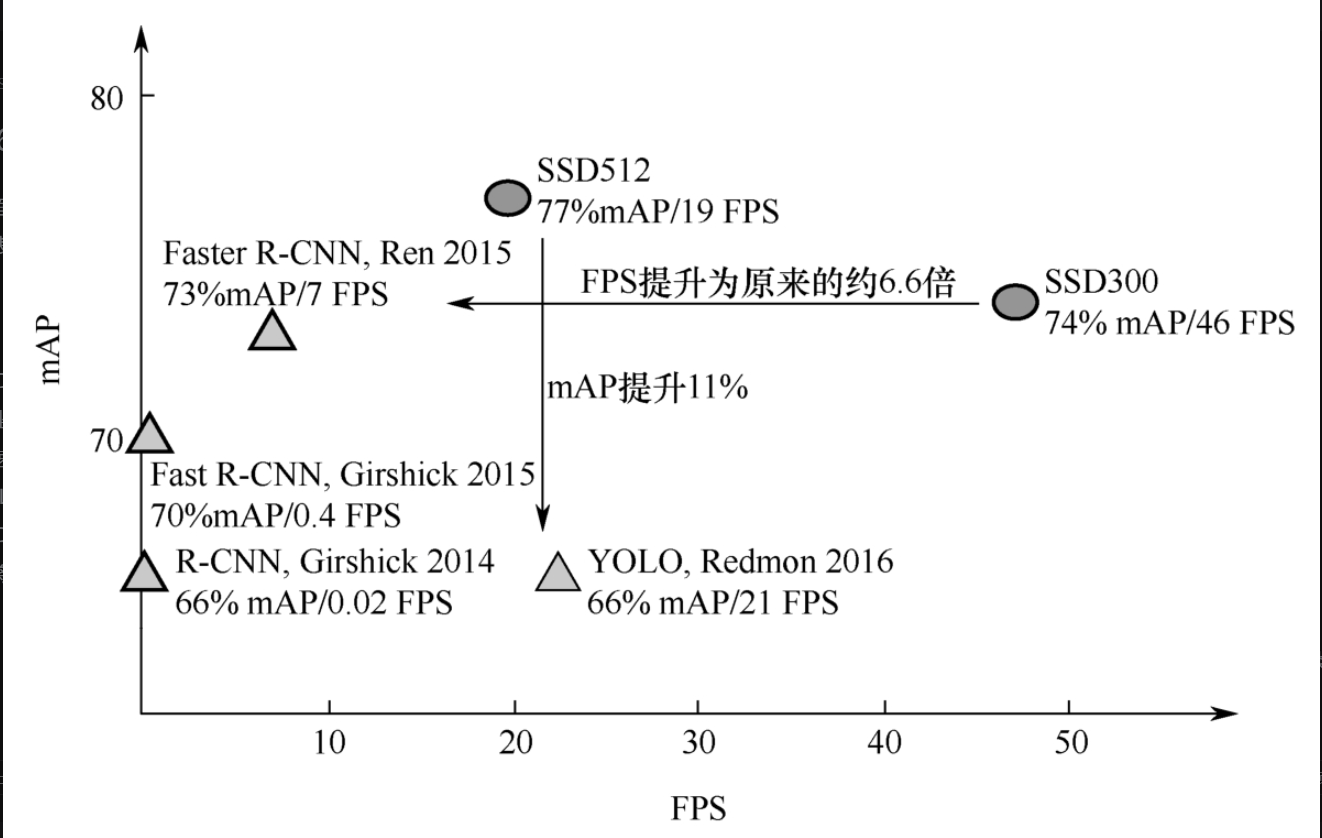
SSD算法的提出时间在YOLOv1之后，YOLOv2之前。在速度和mAP的衡量坐标系上，SSD算法是比较靠右上的，如图7-6-1所示。说明SSD是一个速度与平均精度都很不错的目标检测算法。

在速度方面，SSD512比YOLOv1要差一些，却比R-CNN系列检测算法速度、平均精度都要高。SSD300的速度与平均精度都高于YOLOv1，但是精度低于SSD512。下面将以SSD300为例进行讲解。

图7-6-1 SSD与其他方法速度精度比较

SSD具有如下3个特点。

(1)从YOLO中继承将检测转化为回归的思路，一次完成目标定位与分类。

SSD完全继承了YOLO这种 “回归”（Regression）的思路。所谓“回归”，就是指模型直接输出边界框的坐标和类别概率这些数值，而不是像Faster R-CNN那样先提出候选再判断。这让SSD保持了非常快的速度，适合需要实时检测的场景。

(2)借鉴Faster R-CNN中的锚框，提出相似的建议框

锚框就是预先定义好的一系列不同形状、不同大小的“模板框”。比如有正方形的、有宽扁的、有瘦高的，大大小小各种尺寸。判断一下哪个模板和真实物体最接近，然后对这个模板进行“微调”。比如：“这个瘦高的模板和那个人比较像，我只需要把框往左边拉一点，把它拉高一点，就完美匹配了！”这个“微调”就是预测一个偏移量，而不是凭空生成一个框。

(3)加入基于特征金字塔的检测方式，即在不同感受野的特征图上预测目标。

值得一提的是，之前章节讲到的YOLOv3的三级检测，与SSD在不同感受野上检测目标的原理是一样的。

之前的Faster R-CNN有一个很重要的RPN（区域建议网络），其目的就是生成非常好的包括目标的框，RPN先设置3种不同长宽比的框，再对框进行回归，调整框的位置以让框更好地框住物体。

除此之外，这种做法就是基于感受野的原理，如图7-6-2所示。

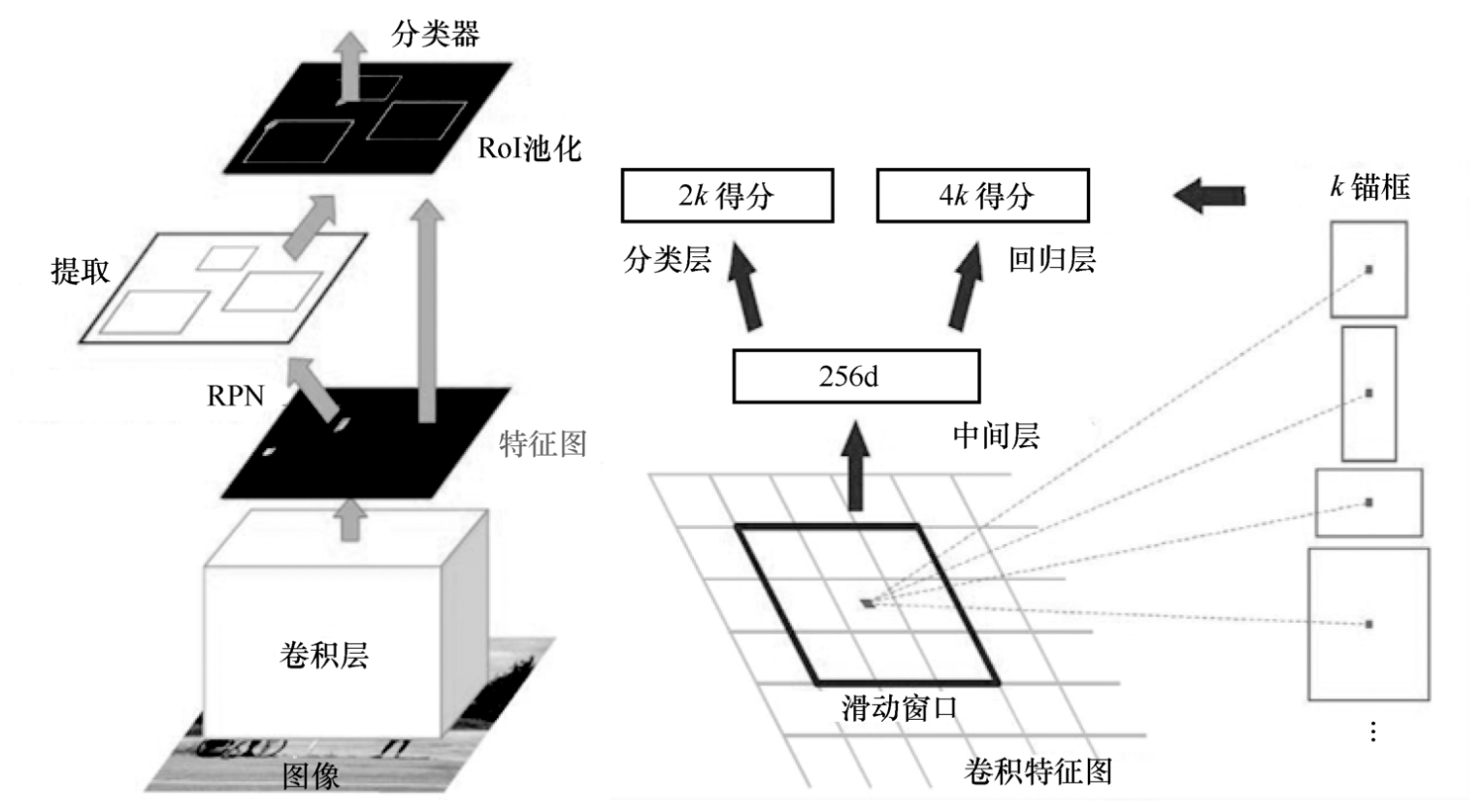
图7-6-2 回顾RPN

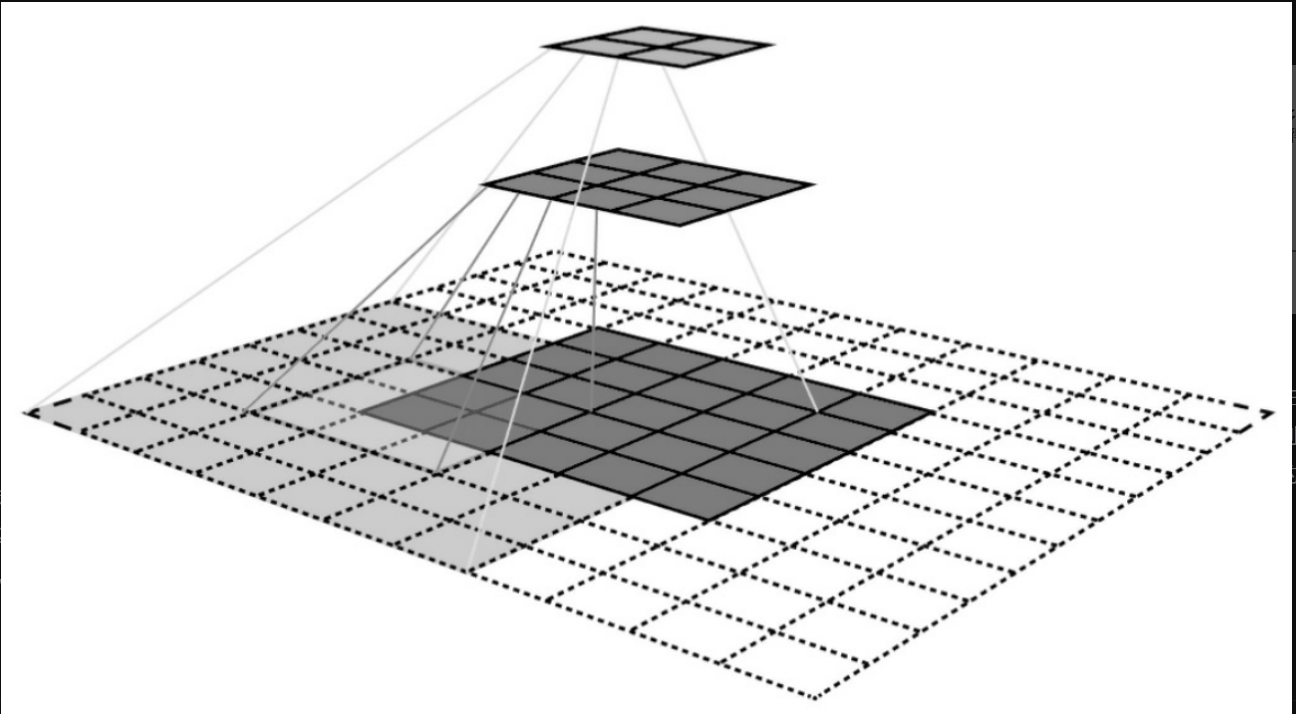
再次回顾卷积神经网络，图7-6-3中黄色特征图对应到原始图像上的感受野就是灰色区域，而绿色特征图在原始图像上对应的感受野就是蓝色部分。

这就是利用感受野在不同的特征图上检测目标。在不断卷积的过程中感受野越来越大，在原始图像上的目标就越来越小，因此，在不同阶段的特征图上检测是一种很精妙的思想。

图7-6-3 卷积神经网络图

概括起来，使用SSD多尺度特征图，在经过步长为2的卷积后，其特征图就为2倍的下采样结果，在两个不同的特征图上检测到的目标大小是不一样的，如图7-6-4所示。

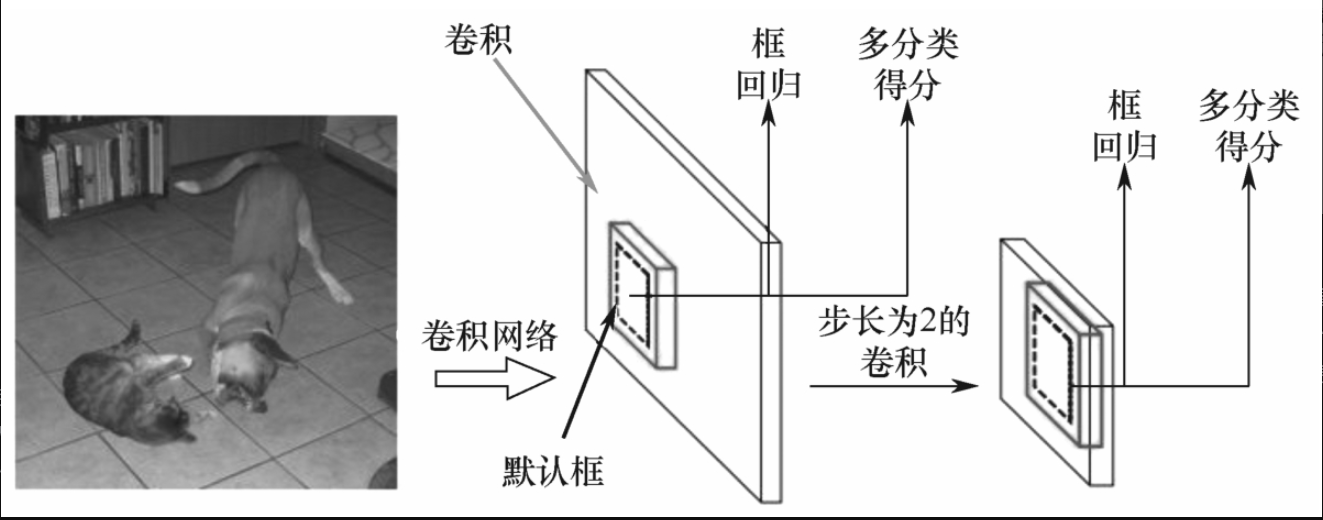
图7-6-4 SSD多尺度特征图

另外，还能从不同阶段卷积层学习到的特征来理解多尺度特征图。

在图7-6-5中，第一层卷积学习到的特征是边缘和斑点，第三层卷积学习到的是纹理，第五层卷积学习到的是目标的初步形状，第八层卷积学习到的是目标物体卡通化。

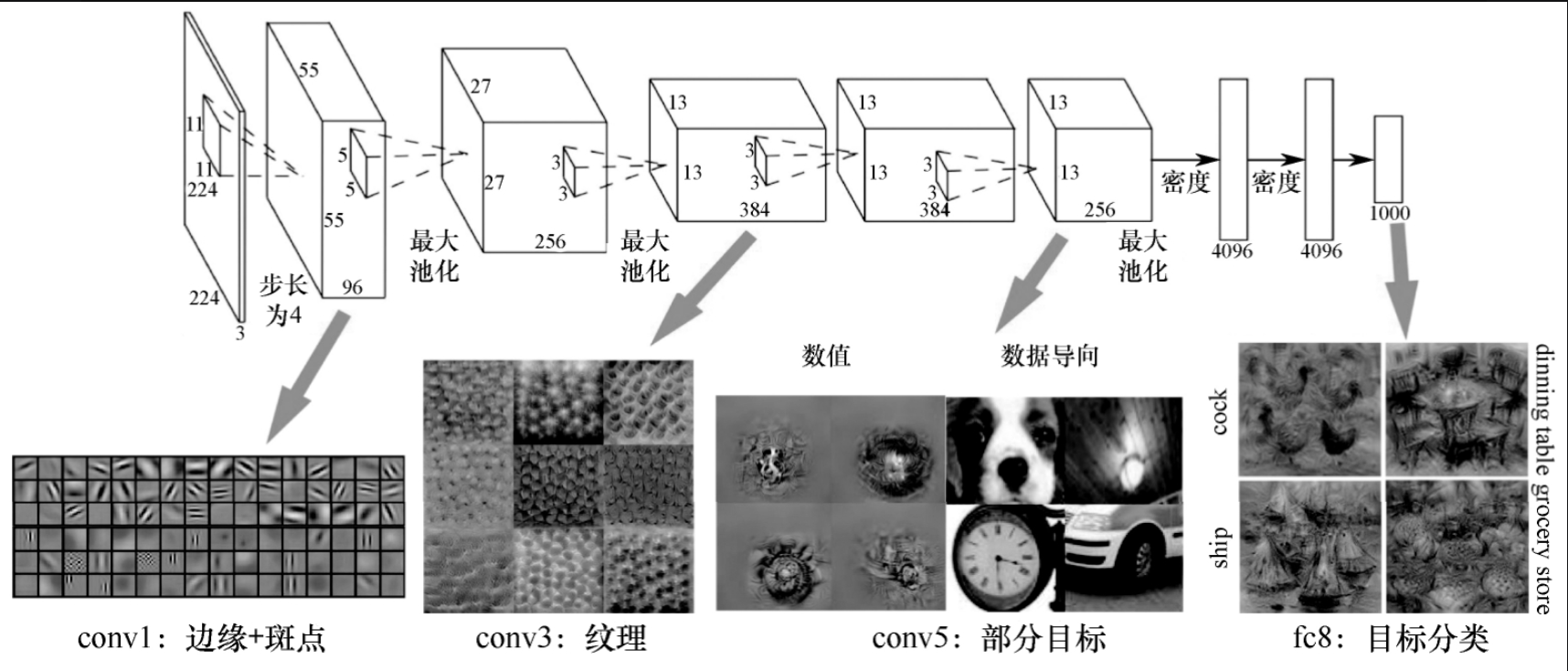
图7-6-5 不同阶段卷积层

SSD为了能更好地利用特征图，延续了Faster R-CNN设置不同长宽比的锚框的做法。

默认框在不同的特征图检测到的物体大小是不一样的，大特征图检测到的是小物体，小特征图检测到的是大物体。

例如，检测图7-6-6中的猫和狗，在8×8的特征图中猫和狗都能使用默认框来检测，对于4×4的特征图，因为其感受野大，所以小的物体就被卷积层忽略掉，留下了大的物体。

SSD300在VGG中对6个特征图进行检测，分别是conv4_3、conv7、conv8_2、conv9_2、conv10_2、conv11_2。对于特征图上每个单元，一般生成6个框，但是有的生成4个框。

检测6个特征图，依次生成5776、2166、600、150、54、4个框，一共8732个框，比YOLOv1产生的框多，但比YOLOv3产生的框少。

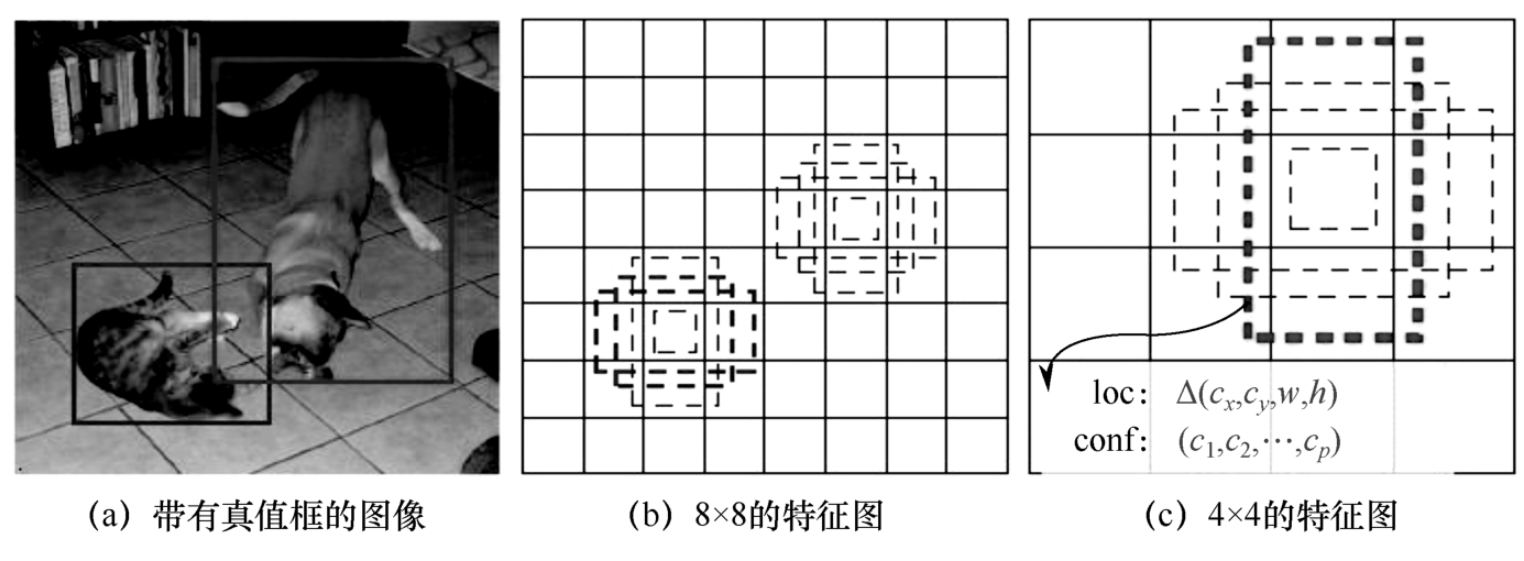
图7-6-6 默认框
如果都使用表7-6-1中的6个尺度特征图进行检测，则SSD能达到74.3%的mAP，如果只使用38×38、19×19、10×10的特征图，则SSD能达到70.7%的mAP，如果只使用19×19特征图，则SSD能达到62.4%的mAP。

表7-6-1 尺度特征图

来逐一解释和整理这几个关于SSD锚框（Default Box）计算的公式。这套机制是SSD实现多尺度检测的核心。

核心思想

SSD同时在多个不同大小的特征图上进行预测。浅层的特征图感受野小，适合检测小物体；深层的特征图感受野大，适合检测大物体。 为了适配不同大小的物体，需要在每个特征图上设置一系列不同大小、不同形状的“模板框”，这些模板框就是锚框。

这些公式的目的就是：系统化地、自动化地生成这些覆盖所有可能尺度和形状的锚框模板。

公式详解

公式 (7-2)：确定不同特征图上的基准尺度

公式：
$s_k = s_{\min} + \frac{s_{\max} - s_{\min}}{m-1}(k-1), \quad k \in [1, m]$

解读：
这个公式用来计算第 k 层特征图上锚框的基准尺度 s_k。

s_min 和 s_max：所有特征图中，最小和最大的基准尺度。图中设为 0.2 和 0.9。
- 注意： 这里的尺度是相对于原图尺寸的比例。例如 s_k=0.2 意味着锚框大小是原图边长的 20%。
m：用于预测的特征图的总层数。例如，如果SSD使用了6层特征图（如VGG版的SSD300），那么 m=6。
k：当前是第几层特征图。k 从 1 到 m。

这个公式做了什么？
它将在 s_min 和 s_max 之间进行线性插值，为每一层特征图分配一个递增的基准尺度。

当 k=1 (最浅的层)： $s1=0.2+0.9−0.25(0)=0.2s_1 = 0.2 + \frac{0.9-0.2}{5}(0) = 0.2$ （检测小物体）
当 k=2： $s2=0.2+0.75(1)=0.34s_2 = 0.2 + \frac{0.7}{5}(1) = 0.34$
…
当 k=m=6 (最深的层)： $s6=0.2+0.75(5)=0.9s_6 = 0.2 + \frac{0.7}{5}(5) = 0.9$ （检测大物体）

简单来说：公式(7-2)决定了每一层特征图主要负责检测多大尺寸的物体，并且让这些尺寸均匀地覆盖从最小（0.2）到最大（0.9）的范围。

公式 (7-3)：计算每个基准尺度下的不同形状的锚框

公式：
对于每个基准尺度 s_k，设置5种宽高比 a_r（即 1, 2, 3, 1/2, 1/3），然后计算锚框的实际宽和高：

$s_k \times \sqrt{a_r}$
$s_k \div \sqrt{a_r}$

解读：
这个公式基于基准尺度 s_k 来生成不同形状的锚框。

a_r = 1：正方形框。 $s_k \times 1 = s_k$ , $s_k \div 1 = s_k$
a_r = 2：宽框。 $s_k \times \sqrt{2} \approx s_k \times 1.414$ , $s_k \div \sqrt{2} \approx s_k \times 0.707$
a_r = 3：更宽的框。
a_r = 1/2：高框（瘦框）。 $s_k \times \sqrt{1/2} \approx s_k \times 0.707$ , $s_k \div \sqrt{1/2} \approx s_k \times 1.414$
a_r = 1/3：更高的框（更瘦的框）。

简单来说：公式(7-3)为每一层的基准尺度 s_k 生成了5个不同形状（胖的、瘦的、方的）的锚框，以适应现实中物体不同的长宽比例。

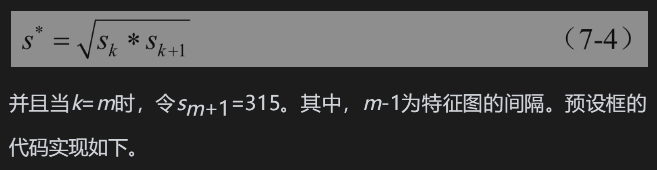
公式 (7-4)：增加额外的正方形锚框

公式：
$s^* = \sqrt{s_k \times s_{k+1}}$

解读：
除了上面5种宽高比的锚框，SSD还为每一层额外增加一个正方形锚框，其尺度不是本层的 s_k，而是本层和下一层尺度的几何平均数 s^*。

为什么？ 为了提供更多一层的尺度覆盖。s^* 的大小介于 s_k 和 s_{k+1} 之间，这样使得每个特征位置预测的锚框在尺度上更具多样性，提高检测的召回率。
对于最顶层（k=m），没有 k+1 层，所以规定 s_{m+1} = 315/300 = 1.05（假设输入图像是300x300）。

简单来说：公式(7-4)在每一层原有的5个锚框基础上，再额外添加1个大小介于本层和下一层之间的正方形锚框，使得每一层的每个位置总共预测6个锚框（5+1）。

总结与整理

假设SSD使用 m=6 层特征图，那么整个锚框的生成过程可以整理为下表：

特征图层 (k)	基准尺度 (s_k)	宽高比 (a_r)	锚框数量/位置	主要负责检测
1 (最浅)	0.2	1, 2, 3, 1/2, 1/3	5	极小的物体
2	~0.34	1, 2, 3, 1/2, 1/3	5	小物体
3	~0.48	1, 2, 3, 1/2, 1/3	5	中小物体
4	~0.62	1, 2, 3, 1/2, 1/3	5	中等物体
5	~0.76	1, 2, 3, 1/2, 1/3	5	中大物体
6 (最深)	0.9	1, 2, 3, 1/2, 1/3	5	大物体
每层额外增加	s = √(s_k × s_{k+1})*	1 (仅为正方形)	+1	补充尺度
总计			(5 + 1) × 6 = 36 种尺寸组合

最终，SSD通过这套精妙的公式，在多个特征层的每个位置上，自动生成了大量不同尺度、不同形状的锚框，从而能够高效且全面地检测图像中各种大小和比例的目标物体。

预设框的代码实现如下。

## //第7章/7.6预设框实现
import math # 导入数学模块，用于使用floor等数学函数# 实践中式(7-2)中$ s_{max} $与$ s_{min} $先扩大100倍向下取整，除以m-1后取整，再除以100
# 这样做是为了避免浮点数精度问题，通过整数运算得到更精确、一致的尺度参数。min_dim = 300  # 输入图像的尺寸（假设为300x300，这是SSD300的标准输入）# 以下列表指定了用于生成预设框的6个特征层的名称。
# 这些层来自SSD的主干网络（如VGG16），其输出特征图尺寸依次减小，用于检测不同尺度的目标。
# conv4_3 ==> 38 x 38  (感受野小，负责检测小目标)
# fc7     ==> 19 x 19
# conv6_2 ==> 10 x 10
# conv7_2 ==> 5 x 5
# conv8_2 ==> 3 x 3
# conv9_2 ==> 1 x 1    (感受野大，负责检测大目标)
mbox_source_layers = ['conv4_3', 'fc7', 'conv6_2', 'conv7_2', 'conv8_2', 'conv9_2']# 初始化最小和最大比例。注意这里扩大了100倍，对应公式中的s_min=0.2, s_max=0.9。
min_ratio = 20 # 即 s_min * 100 = 0.2 * 100
max_ratio = 90  # 即 s_max * 100 = 0.9 * 100# math.floor()函数表示:求一个最接近它的整数，它的值小于或等于这个浮点数。
# 计算尺度比例增长的步长。len(mbox_source_layers)-2 是因为首尾层特殊处理。
# 这里计算的是 (90-20) / (6-2) = 70 / 4 = 17.5，向下取整后 step=17。
step = int(math.floor((max_ratio - min_ratio) / (len(mbox_source_layers)-2)))# 初始化两个列表，用于存储所有特征层上预设框的基准最小尺寸和最大尺寸。
min_sizes = [] # 对应公式中的 s_k
max_sizes = [] # 对应公式中的 s_{k+1}，用于计算额外的基准尺度 s_k*# 循环生成中间特征层（fc7, conv6_2, conv7_2, conv8_2）的尺度。
# range(min_ratio, max_ratio+1, step): 从20开始，到91结束（不包括91），步长为17。
# 生成的ratio序列为: [20, 37, 54, 71, 88]
for ratio in range(min_ratio, max_ratio+1, step):# 将比例ratio转换回相对于图像尺寸的实际像素值。# min_dim * ratio / 100.0 等价于 300 * (ratio/100) = 300 * s_k# 例如：ratio=20 -> min_sizes.append(300 * 0.2) = 60.0min_sizes.append(min_dim * ratio / 100.)# 计算最大尺寸，300 * ( (ratio + step) / 100 )# 例如：ratio=20 -> max_sizes.append(300 * (20+17)/100) = 300 * 0.37 = 111.0max_sizes.append(min_dim * (ratio + step) / 100.)# 手动添加最浅层（conv4_3）和最深层（conv9_2）的尺度，因为它们不适用于上述线性增长规则。
# 为最浅层conv4_3(38x38)添加一个极小的基准框（min_sizes[0]）和一个较小的基准框（max_sizes[0]）。
min_sizes = [min_dim * 10 / 100.] + min_sizes # [30.0, 60.0, 111.0, 162.0, 213.0, 264.0]
max_sizes = [min_dim * 20 / 100.] + max_sizes # [60.0, 111.0, 162.0, 213.0, 264.0, 315.0]# 定义`steps`：表示每个特征层上的一个点（像素）对应原图中的步长（像素数）。
# 其值由 输入图像尺寸 / 特征图尺寸 近似得到。
# 例如：
#   conv4_3: 300 / 38 ≈ 8
#   fc7:     300 / 19 ≈ 16
#   conv6_2: 300 / 10 = 30，但常用32（2^5）作为近似，可能是为了计算效率。
# 这个参数用于将预设框的中心点从特征图坐标映射回原图坐标。
steps = [8, 16, 32, 64, 100, 300]# 定义`aspect_ratios`：为每个特征层指定不同的宽高比组合。
# 每个子列表对应`mbox_source_layers`中相应特征层的宽高比配置。
# 例如：
#   conv4_3: 使用[2] -> 会产生宽高比为 1:2 和 2:1 的两种框（加上默认的1:1，共3种）。
#   fc7:     使用[2, 3] -> 会产生 1:2, 2:1, 1:3, 3:1 四种框（加上默认的1:1，共5种）。
# 宽高比参数用于生成不同形状的预设框，以适应各种形状的目标物体。
aspect_ratios = [[2], [2, 3], [2, 3], [2, 3], [2], [2]]# 打印计算得到的最小和最大尺寸列表，用于验证。
print(min_sizes) # 输出: [30.0, 60.0, 111.0, 162.0, 213.0, 264.0]
print(max_sizes) # 输出: [60.0, 111.0, 162.0, 213.0, 264.0, 315.0]

这段代码的核心目的是为SSD的6个不同尺度的特征图，系统性地生成一系列预设框的配置参数（min_sizes, max_sizes, aspect_ratios）。

尺度（Size）：通过 min_sizes 和 max_sizes 控制。浅层特征图（如 conv4_3）的预设框较小（如30x30），用于检测小目标；深层特征图（如 conv9_2）的预设框较大（如264x264），用于检测大目标。尺度在层与层之间线性增长。
宽高比（Aspect Ratio）：通过 aspect_ratios 控制。为不同层配置不同的宽高比组合，如 [2] 或 [2, 3]，从而生成瘦高、宽扁等不同形状的预设框，以适应行人、车辆等不同形状的目标。
步长（Step）：通过 steps 控制。它将预设框的中心点从特征图坐标（如38x38的网格）映射回原始输入图像坐标（300x300的网格）。

最终，这些参数会被送入后续的 PriorBox 层，在每个特征图的位置上自动生成所有预设框的具体坐标。这些预设框作为模型预测的基准，网络只需要学习目标相对于这些预设框的偏移量和分类置信度即可，大大降低了学习难度。

7 SSD网络架构

上一节阐明了SSD检测算法的指导思想与检测原理，本节详细介绍SSD网络架构。

7.1 SSD网络基础架构

SSD使用VGG-16网络作为基础网络，VGG-16在分类任务中被广泛使用。

VGG-16网络分为5个部分的卷积块，其中第1(c1)、2(c2)个卷积块只有两层卷积层，第3(c3)、4(c4)、5(c5)个卷积块有33个卷积层；卷积块之后紧接全连接6(fc6)、全连接7(fc7)、全连接8(fc8)，最后得到输出，如图7-7-1所示。

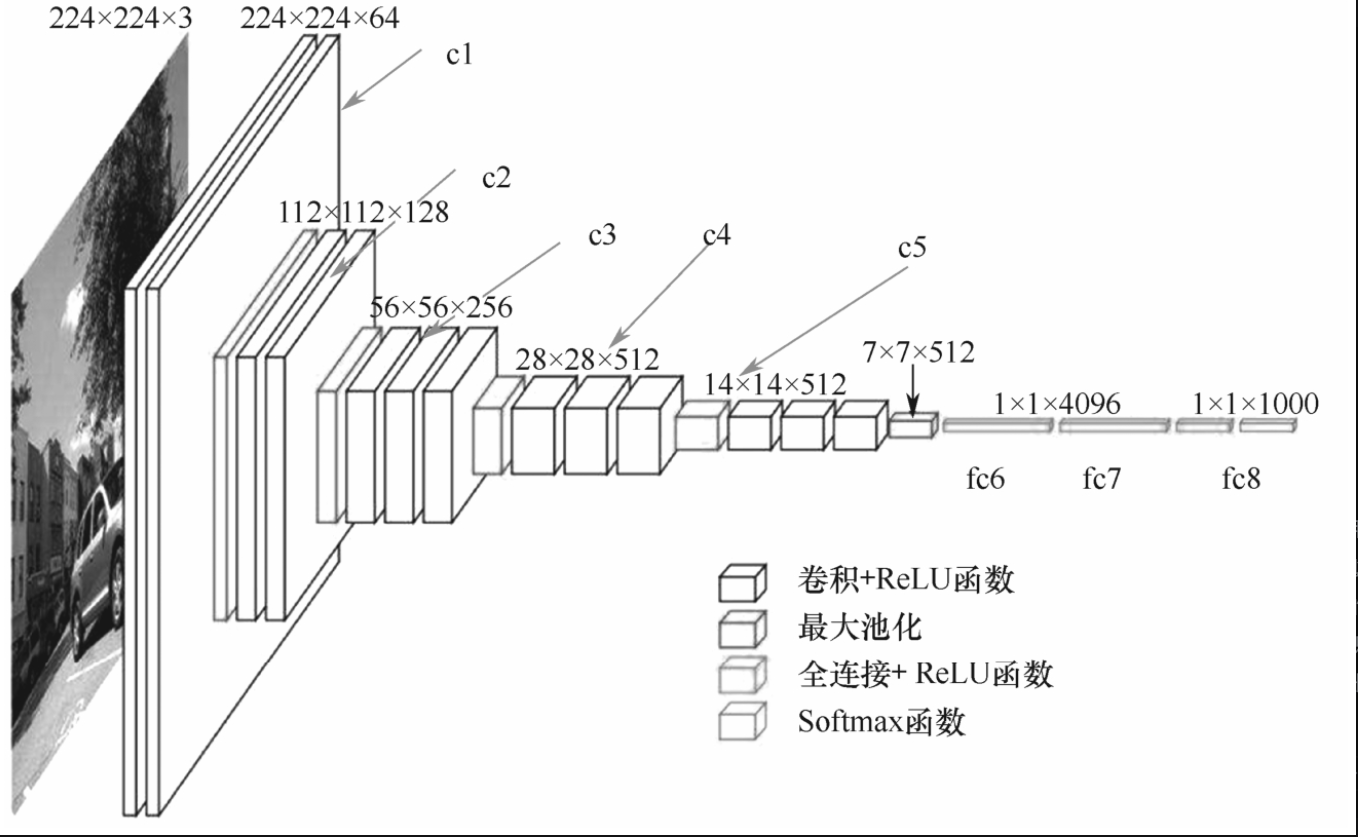
图7-7-1 VGG-16结构

SSD网络是在VGG-16的基础上加以改造，形成以将改造后的VGG网络用于物体检测。

SSD在VGG网络后移除了全连接(fc8)层，增加了6个辅助层，其中5个将被用于多尺度特征图的检测，而VGG-16第四个卷积块的卷积层也作为供检测的特征图。

SSD将VGG-16的fc6和fc7变成了卷积层：con3×3、con1×1。此外，conv6、conv7还进行了扩张卷积。

扩张卷积能在不增加参数与模型复杂度的条件下指数级扩大卷积的视野，经过前面的学习可知卷积的视野相当重要。因为在VGG前段网络卷积的次数相对较少，所以，需要使用扩张卷积来增加视野。

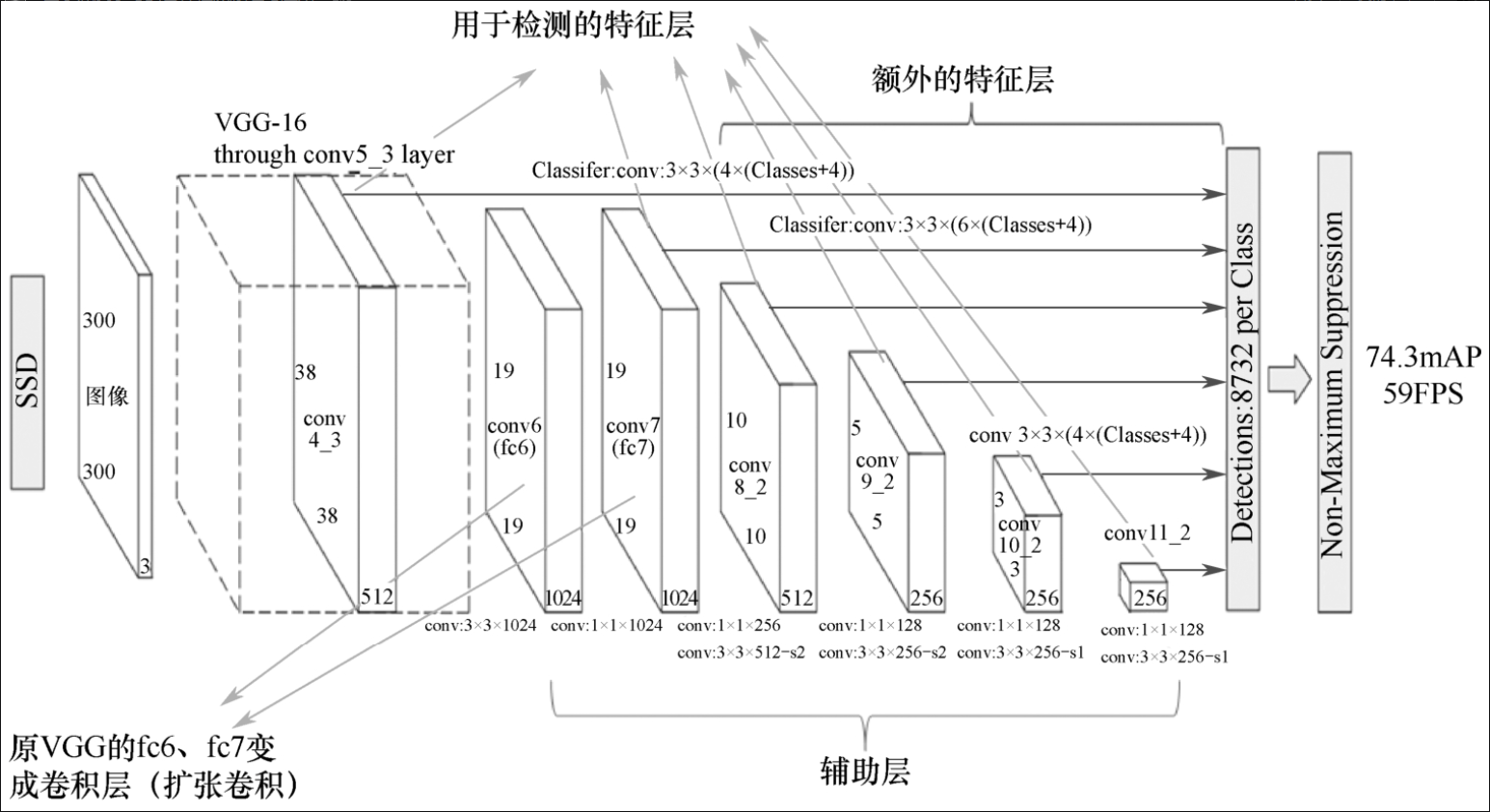
整个SSD网络根据特征图的产生默认框数量计算：

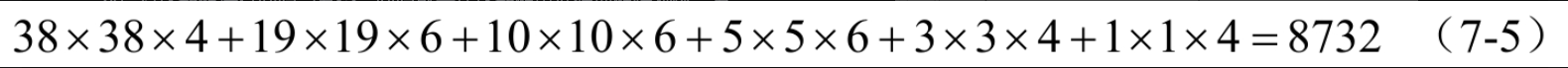
然后将这些框进行回归与分类。回归就是让这些框更准确地框住物体，分类就是将框中的物体正确分类，如图7-7-2所示。

图7-7-2 SSD300计算图示

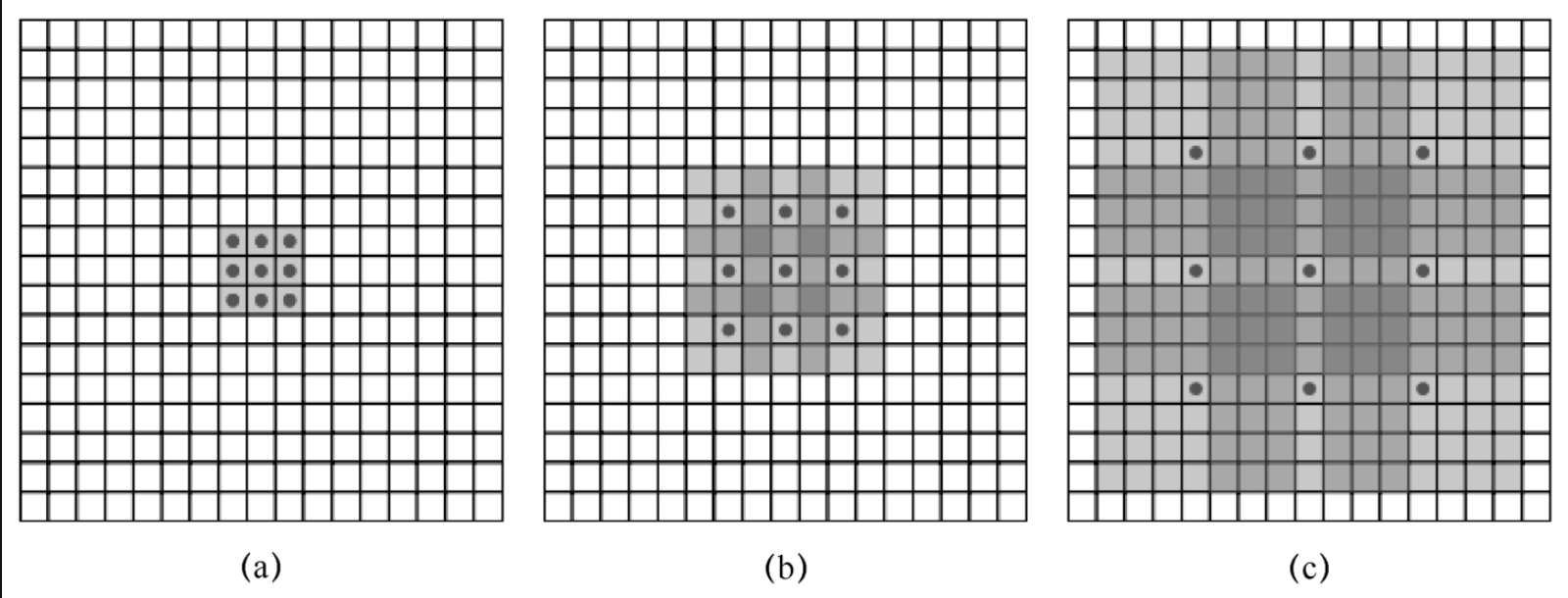
7.2 扩张卷积

如图7-7-3所示，图7-7-3(a)为普通3×3的卷积，在3×3卷积基础上在每两个点之间加上一个格子，再在周围加一层格子，这就是扩张卷积，也被形象地称为带孔卷积。

这样，卷积的视野就从3×3变成了7×7，继续将扩张卷积的扩张率由1变成3，这样视野就扩大为15×15。

图7-7-3 扩张卷积

7.3 SSD与YOLOv3

网络上有很多技术博客比较SSD与YOLOv1的区别，因为SSD网络是在YOLOv1之后提出的，由于前面的小节已经讲解过YOLOv3，所以，这里只列出SSD与YOLOv3的相同点，这样更有利于从本质上讲解SSD原理。

SSD网络与YOLO在本质上相差不大，这样更便于读者抓住目标检测算法的本质。

一阶段方法中SSD与YOLOv3的相同点与相异点如下。

(1)多级检测：YOLOv3设计三级检测机制，而SSD采用金字塔结构，利用conv4-3/conv-7/conv6-2/conv7-2/conv8_2/conv9_2这些层大小不同的特征图，在多个特征图上同时进行Softmax分类和位置回归。
(2)锚框：YOLO3利用聚类得到9个不同尺度的先验框，并分配到3级检测，每级3个尺度；SSD使用3种不同比例的长宽，每个特征图根据序列公式计算边界框大小。

由上述可以看出，SSD与YOLOv3本质上是一样的，YOLOv3更加精巧利索。

SSD 与 YOLOv3 核心特性对比表

特性	SSD (Single Shot MultiBox Detector)	YOLOv3 (You Only Look Once v3)	对比分析 / 本质区别
1. 主干网络 (Backbone)	基于 VGG-16（或其他分类网络）进行修改。相对较浅，特征提取能力有限。	基于自研的 Darknet-53。融合了残差连接，更深且更高效，特征提取能力更强。	YOLOv3使用了更强大、更现代的专用主干网络，这是其性能提升的基础。
2. 锚框 (Anchor) 生成	手动设计公式。通过线性递增的规则公式 (`s_min` -> `s_max`) 为不同特征层计算基准尺寸，再结合预设的宽高比。	数据驱动的聚类。使用 K-means聚类在训练集上统计得到9个最具代表性的先验框尺寸。	YOLOv3的锚框更贴合实际数据分布，提供了更好的初始化，使网络更容易学习。
3. 多尺度预测结构	特征金字塔 (FPN的雏形)。直接利用主干网络中不同深度的原生特征层（如conv4_3, fc7等）进行预测。层与层之间没有特征融合。	特征金字塔网络 (FPN)。通过上采样和拼接，将深层的语义信息传递到浅层，使每个预测层都融合了高分辨率和强语义信息。	这是最核心的改进。YOLOv3的FPN结构使得用于检测小物体的浅层特征也包含了丰富的语义信息，大幅提升了对小物体的检测能力。
4. 预测方式	每个特征点预测固定数量的框（如6个）。分类与置信度预测相对独立。	每个特征点同样预测多个框。但为每个锚框预测一组值，这组值同时包含： - 坐标偏移 - 目标置信度 - 所有类别的分数	两者在形式上相似，但YOLOv3的设计更为集成和紧凑。
5. 分类逻辑	对每个框使用 Softmax 分类。假设类别是互斥的（一个框只能属于一个类）。	对每个类别使用独立的逻辑回归（二元交叉熵）。允许多标签分类（一个框可以同时属于“女人”和“行人”）。	YOLOv3更灵活，适用于更复杂的现实场景（物体可能同时属于多个类别）。
6. 核心优势	结构相对简单，速度较快，是早期一阶段检测器的优秀代表。	在保持实时性的前提下，精度更高，尤其是对小物体的检测能力显著优于SSD。	YOLOv3在速度与精度之间取得了更好的平衡，是更为成熟的架构。
7. 性能表现	速度快，但精度（尤其是mAP）相对YOLOv3较低，小物体漏检较多。	精度更高，在COCO等标准数据集上的mAP指标远超同期SSD，同时保持了实时速度。	YOLOv3通过多项改进，实现了性能的全面领先。

总结与本质

通过表格对比，可以得出以下结论：

核心思想一脉相承：SSD和YOLOv3都遵循“在不同尺度的特征图上直接预测目标”这一核心思想，这是它们同属一阶段检测器且性能优于早期YOLO的关键。
YOLOv3是SSD的“全面升级版”：你可以将YOLOv3理解为集成了当时各种先进技术的“超级SSD”。
- 更强的主干网络：Darknet-53 vs VGG-16
- 更好的先验框：聚类生成 vs 手动设计
- 更先进的多尺度结构：FPN（有特征融合） vs Pyramid（无特征融合）
- 更灵活的分类器：多标签分类 vs 互斥分类
“精巧利索”体现在何处：YOLOv3的设计更数据驱动（锚框聚类）、更符合直觉（浅层特征需要深层语义信息来更好地识别小物体），因此其网络架构虽然更深，但设计更为优雅和高效，最终实现了更高的检测精度。

简单来说，SSD提出了一个强大的多尺度检测框架，而YOLOv3则在此基础上，通过引入FPN、更好的主干网络和聚类锚框等关键技术，将这个框架优化和强化到了新的高度。

7.4 SSD网络检测物体方法

YOLOv3从基础网络中得到的特征图为255个输出通道，在YOLOv3的一级检测中有13×13的单元格，每个单元格中有255个值，255作为单元格的属性；而255=85×3，这就代表每个格子使用3个框预测85个分类。

SDD网络本质上与YOLOv3类似，SSD通过卷积后的通道数进行预测。

如图7-7-4所示，定位输出的是4个数值：中心点x、y，目标框的长宽w、h；预测的是21个类的置信度：20个类别和1个背景类。在大小为5×5的特征图上每个格子生成3个锚框，共生成75个框。

SSD为了对物体的位置回归和物体分类，还需要进行一个3×3的卷积，这是为了在深度学习的矩阵运算中将矩阵无缝对应到预测的类别（或者位置）上。

例如，在图7-7-4中，定位下面的特征图（矩阵）大小为5×5×12，因为5×5×12=5×5×3×4：其中的3对应3个框，4对应预测出的4个位置(x、y、w、h)，这样就完成了对框位置的预测。

置信度下面的经过3×3卷积的特征图尺寸为5×5×63，而5×5×63=5×5×3×21：其中3对应3个框，21对应21个类别；3×3卷积就是为了适配框的位置预测与物体的类别预测。

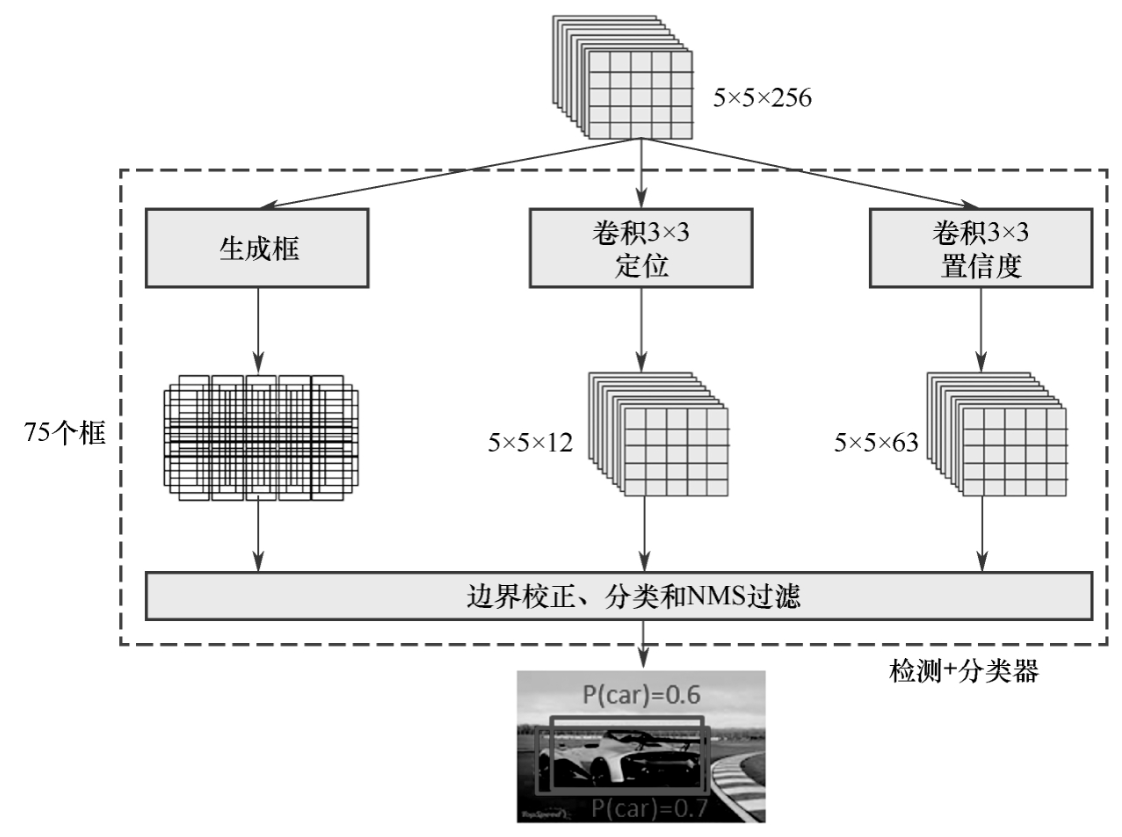
图7-7-4 SSD网络
这种通过不同卷积核个数来对物体位置与分类进行预测的方法是十分“精妙”的。

8 SSD网络损失函数

前面阐明了SSD检测算法指整体网络架构，本节详细讲解SSD网络的损失函数。神经网络算法的损失函数就是整个算法的数学支撑。

8.1 默认框匹配策略

在SSD中产生的用来框住目标的框称为候选框。候选框的匹配策略就是怎样去确定产生的默认框的正类和负类。

SSD计算损失的过程中只使用正类默认框，而丢弃负类的默认框。

SSD网络产生默认框后确认正类框的规则如下：默认框与目标物体的IoU大于0.5的就为正类框，否则就为负类框，因此，SSD网络有可能产生多个正类默认框，而之前的YOLO算法只使用最大IoU的作为正类匹配项。

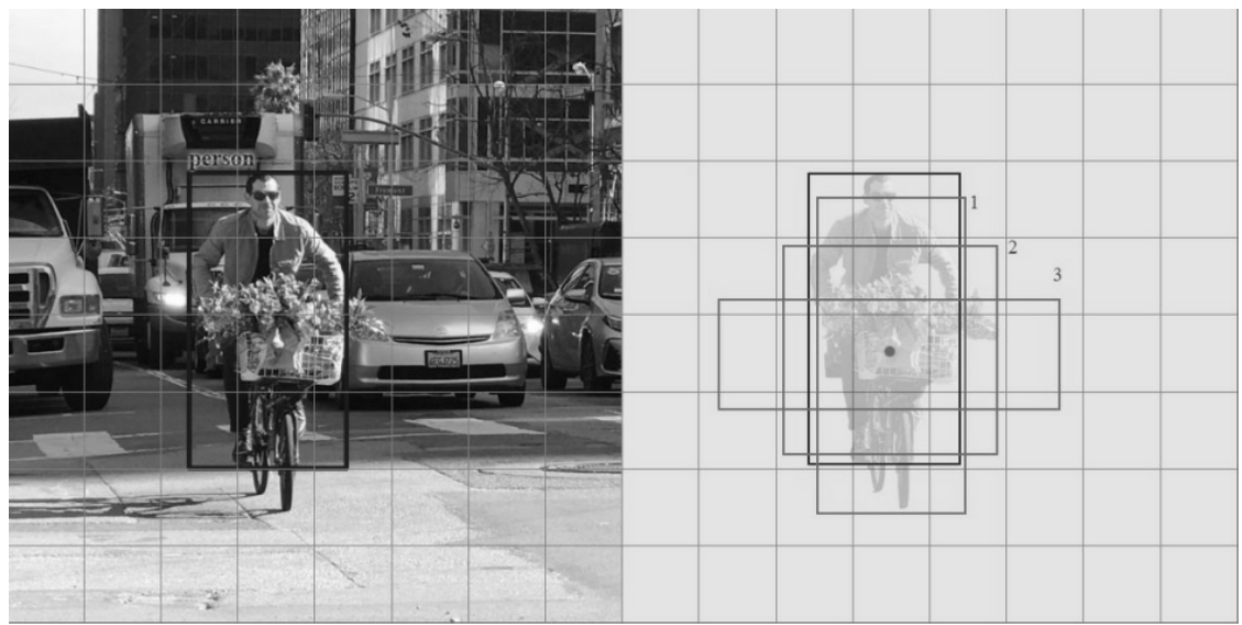
如图7-8-1所示，图中蓝色框为真值框，而SSD生成的默认框只有图中1号、2号、3号框比较接近真值框，然而，3号框与真值框的IoU都小于0.5就是负类框，只有1号、2号框与真值框的IoU都大于0.5才属于正类框。

得到了正类的默认框继而就能使用这些正类的默认框来计算损失函数。**总的来说，SSD网络的默认框匹配策略就是用多个接近真值框的默认框来预测真值框，**这种方法使预测的结果更加多样化，更加稳定。

图7-8-1 默认框策略

8.2 损失函数

SSD的损失函数是其核心组成部分，它指导网络如何同时学习“分类”和“定位”两个任务。其总损失函数是置信度损失（Confidence Loss） 和定位损失（Location Loss） 的加权和。

SSD 损失函数核心解析

总损失函数 (Overall Loss Function)

$\frac{1}{N} \left[ L_{\text{conf}}(x, c) + \alpha L_{\text{loc}}(x, l, g) \right]$

L(x, c, l, g)：总损失。
N：与真实框（Ground Truth）成功匹配的正样本预设框（Positive Prior Boxes）的数量。如果N=0，则损失设为0。
α：一个权重参数，用于平衡分类损失和定位损失的重要性。在大多数实现中（如论文所述），α 默认为 1。
L_{\text{conf}}(x, c)：置信度损失（详见第二部分）。
L_{\text{loc}}(x, l, g)：定位损失（详见第三部分）。

通俗理解： 总损失就是让网络在“判断对不对”（分类）和“框得准不准”（回归）两个方面都做好，并用 N 来归一化，避免正样本数量过多或过少导致训练不稳定。

置信度损失 (Confidence Loss)

$Lconf(x,c)=−∑i∈PosNxijplog⁡(c^ip)−∑i∈Neglog⁡(c^i0),wherec^ip=exp⁡(cip)∑pexp⁡(cip) L_{\text{conf}}(x, c) = -\sum_{i \in \text{Pos}}^N x_{ij}^p \log(\hat{c}_i^p) - \sum_{i \in \text{Neg}} \log(\hat{c}_i^0), \quad \text{where} \quad \hat{c}_i^p = \frac{\exp(c_i^p)}{\sum_p \exp(c_i^p)}$

i：预设框（Prior Box）的索引。
p：类别索引（p=0 通常代表“背景”类）。
x_{ij}^p：一个指示符。取值为 {1, 0}。
- x_{ij}^p = 1：表示第 i 个预设框与第 j 个真实框匹配（即它们的IoU大于一个阈值），并且这个真实框的类别是 p。这就是正样本（Positive）。
- x_{ij}^p = 0：表示不匹配。
c_i^p：网络对第 i 个预设框预测为类别 p 的原始分数。
\hat{c}_i^p：对原始分数应用 Softmax 函数 后得到的归一化概率，表示该预设框属于类别 p 的置信度。
Pos：所有正样本的集合。
Neg：所有负样本（与任何真实框的IoU都小于阈值，即被判断为背景）的集合。

公式解读：

第一项 -\sum_{i \in \text{Pos}}^N ...：计算所有正样本的损失。鼓励网络将这些框正确分类到它们对应的真实类别 p（而不是背景或其他类别）。
第二项 -\sum_{i \in \text{Neg}} ...：计算所有负样本的损失。鼓励网络将这些框预测为“背景”（p=0），即降低它们的“物体置信度”。

本质： 这是一个典型的多类别交叉熵损失（Cross-Entropy Loss），用于解决分类问题。

定位损失 (Location Loss)

$Lloc(x,l,g)=∑i∈PosN∑m∈{cx,cy,w,h}xijksmoothL1(lim−g^jm) L_{\text{loc}}(x, l, g) = \sum_{i \in \text{Pos}}^N \sum_{m \in \{cx, cy, w, h\}} x_{ij}^k \text{smooth}_{L1}(l_i^m - \hat{g}_j^m)$

3.1 预测值与真实值的编码：
网络不直接预测框的绝对坐标，而是预测相对于某个预设框的偏移量。同样，真实值也被编码为这种偏移量形式，这样更易于网络学习和优化。

预测值 l_i^m：网络预测的第 i 个框对于参数 m（中心点x,y或宽高w,h）的偏移量。
真实偏移量 \hat{g}_j^m：计算第 j 个真实框相对于匹配的第 i 个预设框的偏移量，计算公式如下：
$g^jcx=gjcx−dicxdiwg^jcy=gjcy−dicydihg^jw=log⁡(gjwdiw)g^jh=log⁡(gjhdih) \begin{aligned} \hat{g}_j^{cx} &= \frac{g_j^{cx} - d_i^{cx}}{d_i^w} \quad &\hat{g}_j^{cy} &= \frac{g_j^{cy} - d_i^{cy}}{d_i^h} \\ \hat{g}_j^{w} &= \log(\frac{g_j^w}{d_i^w}) \quad &\hat{g}_j^{h} &= \log(\frac{g_j^h}{d_i^h}) \end{aligned}$
- g_j：真实框（Ground Truth）的参数。
- d_i：预设框（Prior Box）的参数。
- 中心点偏移 (cx, cy)：用预设框的宽高进行归一化，使得偏移量不受框的绝对大小影响。
- 宽高偏移 (w, h)：采用比例的对数形式。这样可以将缩放因子（大于1或小于1）的乘法运算转化为加法的形式，更符合线性回归的特性。

3.2 损失函数：Smooth L1 Loss
定位损失使用 Smooth L1 Loss 而不是普通的 L2 损失（均方误差）。
$\text{smooth}_{L1}(x) = \begin{cases} 0.5x^2 & \text{if } |x| < 1 \\ |x| - 0.5 & \text{otherwise} \end{cases}$

优点：
1. 在 x 较小时，它的行为像 L2 Loss，具有平滑的梯度，利于精细调整。
2. 在 x 较大时，它的行为像 L1 Loss，对离群点（预测值与真实值相差很大的点）不那么敏感，比 L2 Loss 更稳定，不易因个别异常样本而导致梯度爆炸。

公式解读： 定位损失只针对正样本（i ∈ Pos） 计算。对于每一个正样本，计算其预测的偏移量 l 和真实偏移量 ĝ 在四个坐标参数上的 Smooth L1 损失，然后求和。

总结表格

组成部分	数学形式	作用	计算对象	关键特点
总损失	`L = (Confidence_Loss + α * Location_Loss) / N`	综合衡量分类和定位的性能	所有预设框	用 `N` 归一化，`α` 平衡权重
置信度损失	Softmax + 交叉熵	判断“是什么”或“是不是背景”	所有预设框（正+负）	正样本学分类，负样本学抑制
定位损失	Smooth L1 Loss	学习如何“微调”框的位置和大小	仅正样本预设框	预测偏移量而非绝对坐标，使用Smooth L1更稳定

SSD 损失函数构成总表

组成部分	数学表达式	计算内容与目的	计算对象	关键特点与说明
总损失函数 (Overall Loss)	$g)=\frac{1}{N}\left[ L_{\text {conf }}(x, c)+\alpha L_{\text {loc }}(x, l, g)\right]$ (式 7-6)	综合衡量模型在分类（是什么）和定位（在哪）两个任务上的总误差。	所有匹配的预设框	• $N$ ：与真实框成功匹配的正样本预设框数量，用于归一化。 • $α\alpha$ ：平衡两项损失的权重，通常设为 1。
置信度损失 (Confidence Loss)	$Nxijplog⁡(c^ip)−∑i∈ Neg log⁡(c^i0)L_{\text {conf }}(x, c)=-\sum_{i \in \text { Pos }}^{N} x_{i j}^{p} \log \left(\hat{c}_{i}^{p}\right)-\sum_{i \in \text { Neg }} \log \left(\hat{c}_{i}^{0}\right)$ $c^ip=exp⁡(cip)∑pexp⁡(cip)\hat{c}_{i}^{p}=\frac{\exp \left(c_{i}^{p}\right)}{\sum_{p} \exp \left(c_{i}^{p}\right)}$ (式 7-7)	计算分类误差。促使模型将正样本分类正确，并将负样本判断为背景。	所有预设框（正样本+负样本）	• 正样本项 ( $\in Pos$ ): 鼓励预测类别 $p$ 的概率 $c^ip\hat{c}_{i}^{p}$ 接近 1。 • 负样本项 ( $\in Neg$ ): 鼓励预测背景 ( $p = 0$ ) 的概率 $c^i0\hat{c}_{i}^{0}$ 接近 1。 • 本质是 Softmax + 交叉熵损失。
定位损失 (Location Loss)	$N∑m∈{cx,cy,w,h}xijksmooth⁡L1(lim−g^jm)L_{\text {loc }}(x, l, g)=\sum_{i \in \text { Pos }}^{N} \sum_{m \in\{c x, c y, w, h\}} x_{i j}^{k} \operatorname{smooth}_{\mathrm{L} 1}\left(l_{i}^{m}-\hat{g}_{j}^{m}\right)$ (式 7-8)	计算边界框坐标的回归误差。促使正样本预测框的位置和大小尽可能接近真实框。	仅正样本预设框	• 使用 Smooth L1 Loss 而非 L2 Loss，对异常值更鲁棒。 • 计算的是预测的偏移量 $l_i^m$ 与真实的偏移量 $g^jm\hat{g}_j^m$ 之间的差异。
偏移量计算 (用于定位损失)	$g^jcx=gjcx−dicxdiw\hat{g}_{j}^{c x}=\frac{g_{j}^{c x}-d_{i}^{c x}}{d_{i}^{w}}$ $g^jcy=gjcy−dicydih\hat{g}_{j}^{c y}=\frac{g_{j}^{c y}-d_{i}^{c y}}{d_{i}^{h}}$ $g^jw=log⁡(gjwdiw)\hat{g}_{j}^{w}=\log\left(\frac{g_{j}^{w}}{d_{i}^{w}}\right)$ $g^jh=log⁡(gjhdih)\hat{g}_{j}^{h}=\log\left(\frac{g_{j}^{h}}{d_{i}^{h}}\right)$	将真实框的绝对坐标编码为相对于预设框的偏移量，这是网络需要学习和预测的目标。	-	• 中心坐标 ( $c x, cy$ ): 用预设框的宽高进行归一化，得到尺度不变的偏移。 • 宽高 ( $w, h$ ): 使用比例的对数，将乘法关系转化为线性关系，更易回归。