Java数据结构 - 二叉树

1.二叉树给基本介绍

二叉树是一种非线性的数据结构，每一个节点的孩子节点不超过2个（度不超过2），通常会定义一个根节点root，一个节点可以有左孩子节点 left 和右孩子节点 right；

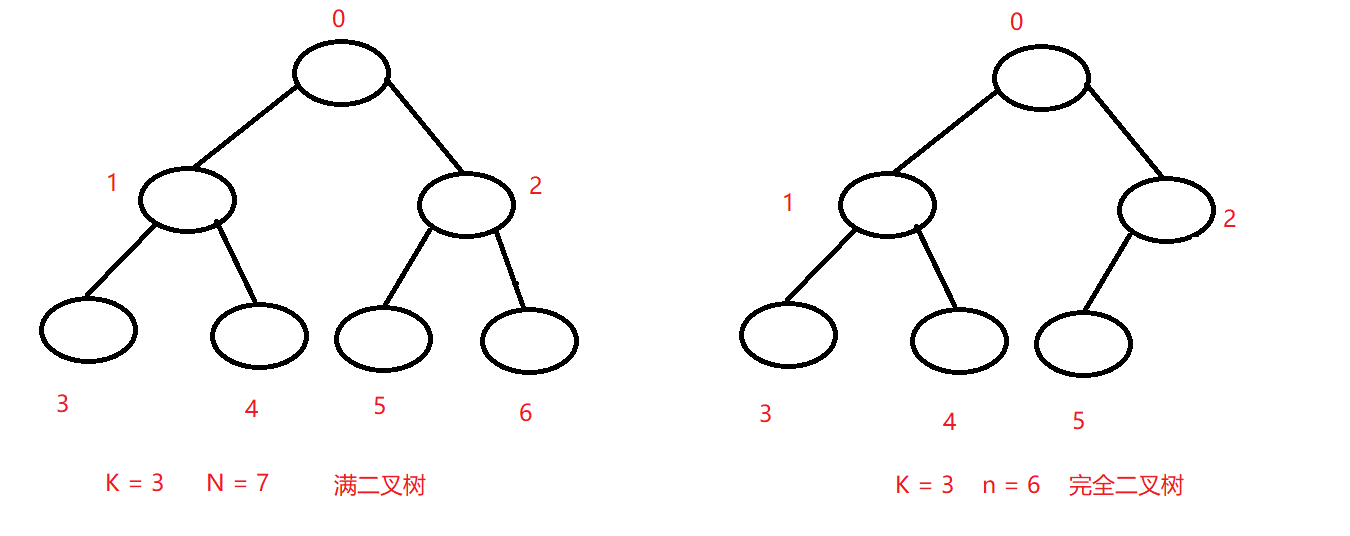
如果一棵二叉树从上到下，从左往右（除最后一层）的每一个节点都有两个孩子节点（最后一层节点度为0），这样的一棵二叉树可以称为满二叉树；

一棵二叉树有n个节点，深度为K，深度为K，有N个节点的满二叉树从上到下，由左往右 0 - N 编号，有且仅当这一棵二叉树的n个节点与这一棵满二叉树从0 - n的编号一一对应时，这样的一棵二叉树可以成为完全二叉树，当n等于N时，满二叉树也是完全二叉树，所以满二叉树是完全二叉树中的一种特殊二叉树。

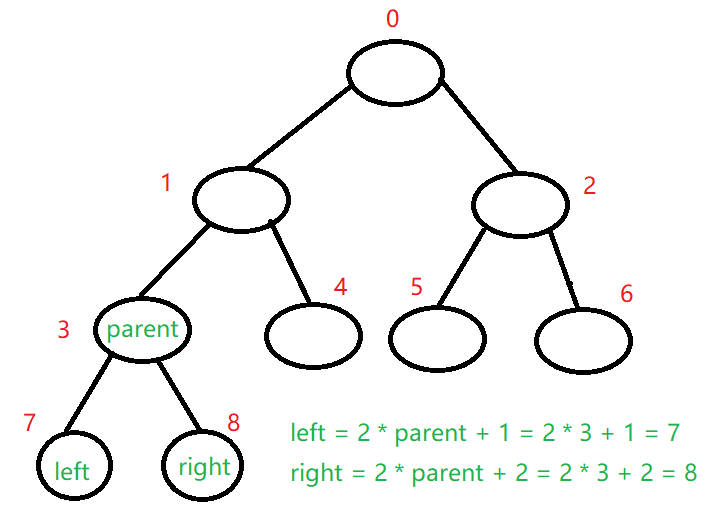
孩子节点的计算,假设一棵二叉树有n个节点，父亲节点的编号为parent.

如果满足 paretnt * 2 + 1 < n,没有左孩子节点，否则左孩子节点为left = parent * 2 +1；

如果满足 parent * 2 + 2 < n,没有右孩子节点，否则右孩子节点为right = parent * 2 + 2；

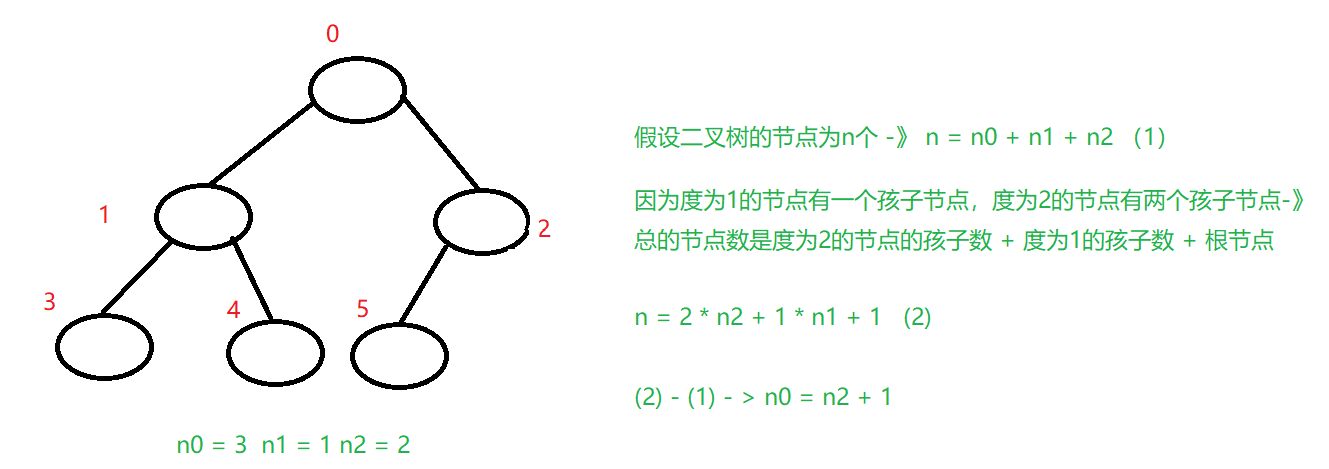
假设一棵二叉树度为0的节点右n0个，度为1的节点有n1个，度为2的节点有n2个，满足n0 = n2 + 1

2.二叉树的使用

2.1 二叉树的创建

在使用二叉树前，可以先创建一棵二叉树，可以是随机创建一棵二叉树或者创建一颗有规律的二叉树，此处创建一棵随机的二叉树。

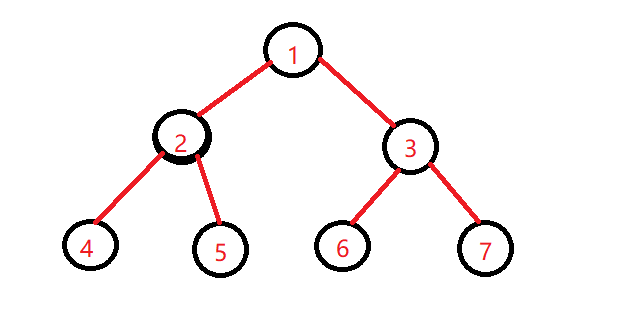
如上图所示创建一颗二叉树，提供一个数组，遍历数组元素，创建节点的同时构建二叉树。

import java.util.LinkedList;
import java.util.Queue;/*** 二叉树的创建*/
public class BinaryTree {//创建一个节点类static class TreeNode{//左右孩子节点TreeNode left;//左孩子TreeNode right;//右孩子//存放值int val;public TreeNode(int val){this.val = val;}}//根节点TreeNode root;//创建根节点public  TreeNode createBinaryTree(int[] values){int len = values.length;//空数组if(len == 0) return null;//只有一个元素if(len == 1) {root.val = values[0];return root;}//多个元素：借助队列，层序创建Queue<TreeNode> q = new LinkedList<>();root = new TreeNode(values[0]);q.offer(root);int i = 1;//数组下标while(!q.isEmpty() && i < len) {int size = q.size();//第一层1个，第二层2个 -- n层 2^(n-1)while(size-- != 0){//获得“父节点”TreeNode cur = q.poll();//创建孩子节点的同时入队列，同时要防止数组越界if(i < len){ cur.left = new TreeNode(values[i++]);q.offer(cur.left);}if(i < len){cur.right = new TreeNode(values[i++]);q.offer(cur.right);}}}return root;}public static void main(String[] args) {BinaryTree b = new BinaryTree();//创建二叉树TreeNode r = b.createBinaryTree(new int[]{1,2,3,4,5,6,7});}
}

2.2 层序遍历

创建好二叉树后，可以通过层序遍历将二叉树每一层节点的值输出打印。

//层序遍历public void levelOrder(){//1.创建队列Queue<TreeNode> queue = new LinkedList<>();//将根节点加入队列queue.offer(root);//2.第一层循环int i = 1;while(!queue.isEmpty()){//3.第二层循环int size = queue.size();System.out.print("第" + i  + "层节点值：");while(size-- != 0){//弹出节点TreeNode tem = queue.poll();//打印System.out.print(tem.val + " ");//左右节点加入队列,不为空才加入if(tem.left != null)queue.offer(tem.left);if(tem.right != null)queue.offer(tem.right);}i++;System.out.println();}}public static void main(String[] args) {BinaryTree b = new BinaryTree();TreeNode r = b.createBinaryTree(new int[]{1,2,3,4,5,6,7});b.levelOrder();}

2.3 前，中，后序遍历

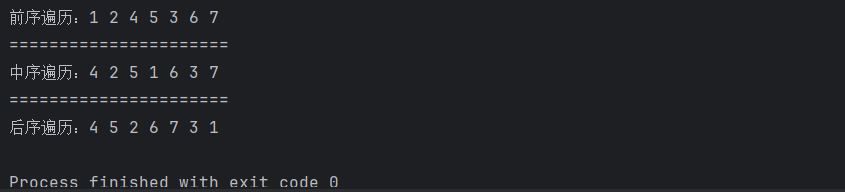
前序遍历是将二叉树都按照根节点打印后，打印左子树节点，再打印右子树节点，每一棵子树都按照“根，左，右”的打印规则打印，直到遍历完二叉树。

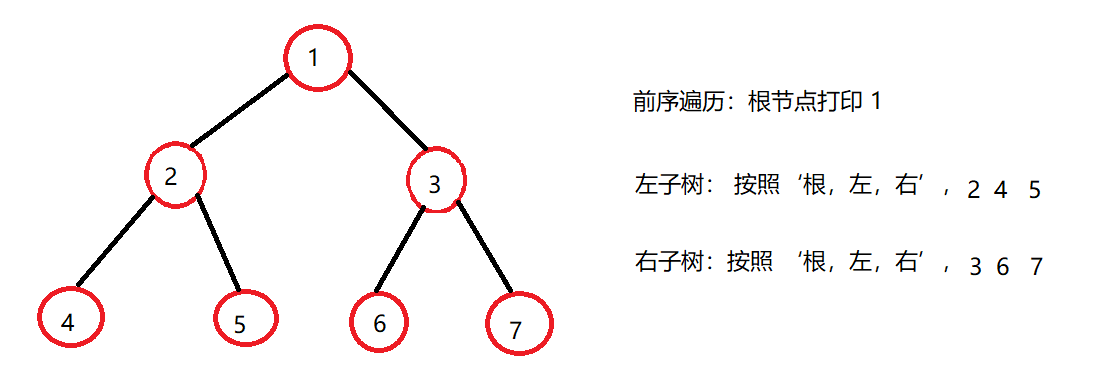
  private void preOrder(TreeNode root){//递归结束条件if(root == null) return;//按照根左右递归System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}//前序遍历public void preOrder(){if(root == null) return;//封装一层函数preOrder(root);}public static void main(String[] args) {BinaryTree b = new BinaryTree();TreeNode r = b.createBinaryTree(new int[]{1,2,3,4,5,6,7});System.out.print("前序遍历：");b.preOrder();}

中序遍历是按照‘左，根，右’的方式遍历二叉树。

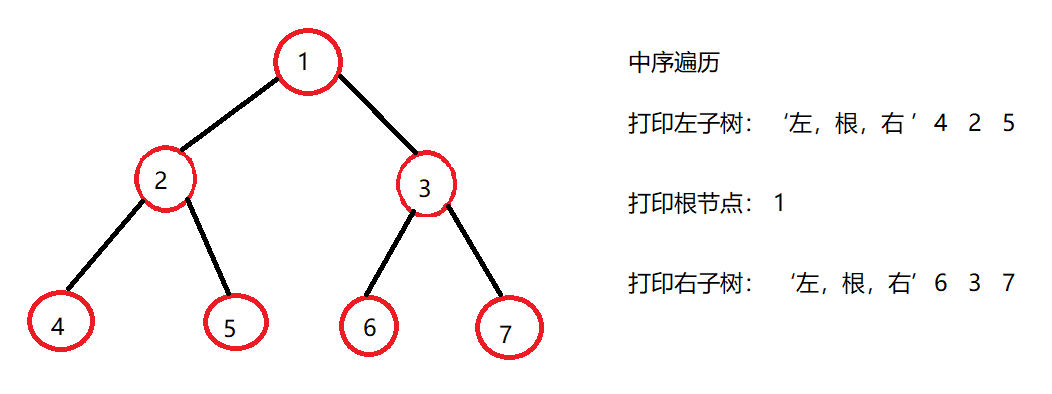
private void inOrder(TreeNode root){//递归结束条件if(root == null) return;//按照左根右递归inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}//前序遍历public void inOrder(){if(root == null) return;//封装一层函数inOrder(root);}public static void main(String[] args) {BinaryTree b = new BinaryTree();TreeNode r = b.createBinaryTree(new int[]{1,2,3,4,5,6,7});System.out.print("前序遍历：");b.preOrder();System.out.println();System.out.println("======================");System.out.print("中序遍历：");b.inOrder();}

后序遍历按照‘左 右 根’的方式遍历二叉树。

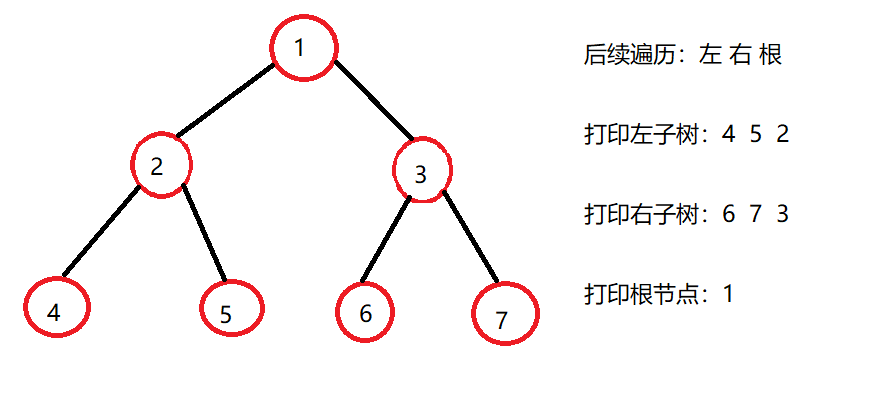
 private void postOrder(TreeNode root){//递归结束条件if(root == null) return;//按照左右根递归postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}//前序遍历public void postOrder(){if(root == null) return;//封装一层函数postOrder(root);}public static void main(String[] args) {BinaryTree b = new BinaryTree();TreeNode r = b.createBinaryTree(new int[]{1,2,3,4,5,6,7});// b.levelOrder();// System.out.println("=================");System.out.print("前序遍历：");b.preOrder();System.out.println();System.out.println("======================");System.out.print("中序遍历：");b.inOrder();System.out.println();System.out.println("======================");System.out.print("后序遍历：");b.postOrder();System.out.println();}

2.2 二叉树节点个数

按照层序遍历的思想，借助队列，每加入一个节点入队列，size++。

public int size(){int size = 0;if(root == null) return size;//1.创建队列Queue<TreeNode> queue = new LinkedList<>();//将根节点加入队列queue.offer(root);size++;//2.第一层循环while(!queue.isEmpty()){//3.第二层循环int size1 = queue.size();while(size1-- != 0) {//弹出节点TreeNode tem = queue.poll();if (tem.left != null) {queue.offer(tem.left);size++;}if (tem.right != null){queue.offer(tem.right);size++;}}}return size;}public static void main(String[] args) {BinaryTree b = new BinaryTree();b.createBinaryTree(new int[]{1,2,3,4,5,6,7});System.out.println("二叉树的节点个数为：" + b.size());}

2.3 获取第K层元素个数

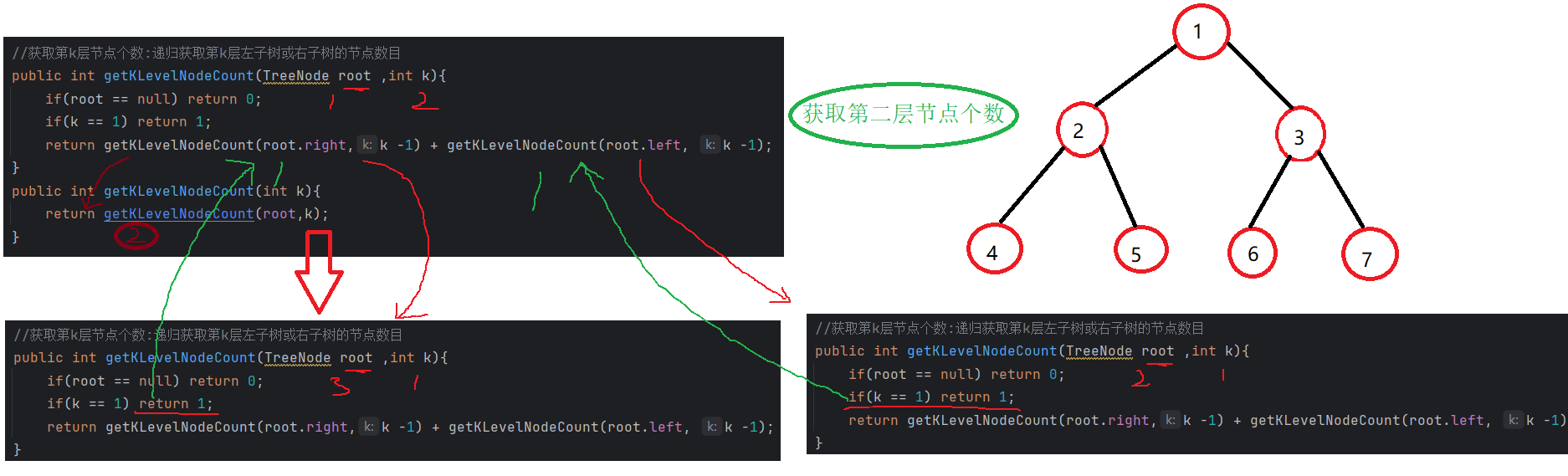
通过递归实现：判断根节点，如果根节点为空返回0，只有根节点一个节点，k =1，返回1，其他情况返回递归左子树和右子树的和。

//获取第k层节点个数:递归获取第k层左子树或右子树的节点数目public int getKLevelNodeCount(TreeNode root ,int k){if(root == null) return 0;if(k == 1) return 1;return getKLevelNodeCount(root.right,k -1) + getKLevelNodeCount(root.left, k -1);}public int getKLevelNodeCount(int k){return getKLevelNodeCount(root,k);}public static void main(String[] args) {BinaryTree b = new BinaryTree();b.createBinaryTree(new int[]{1,2,3,4,5,6,7});System.out.println(b.getKLevelNodeCount(2));}

2.4 获取二叉树的高度

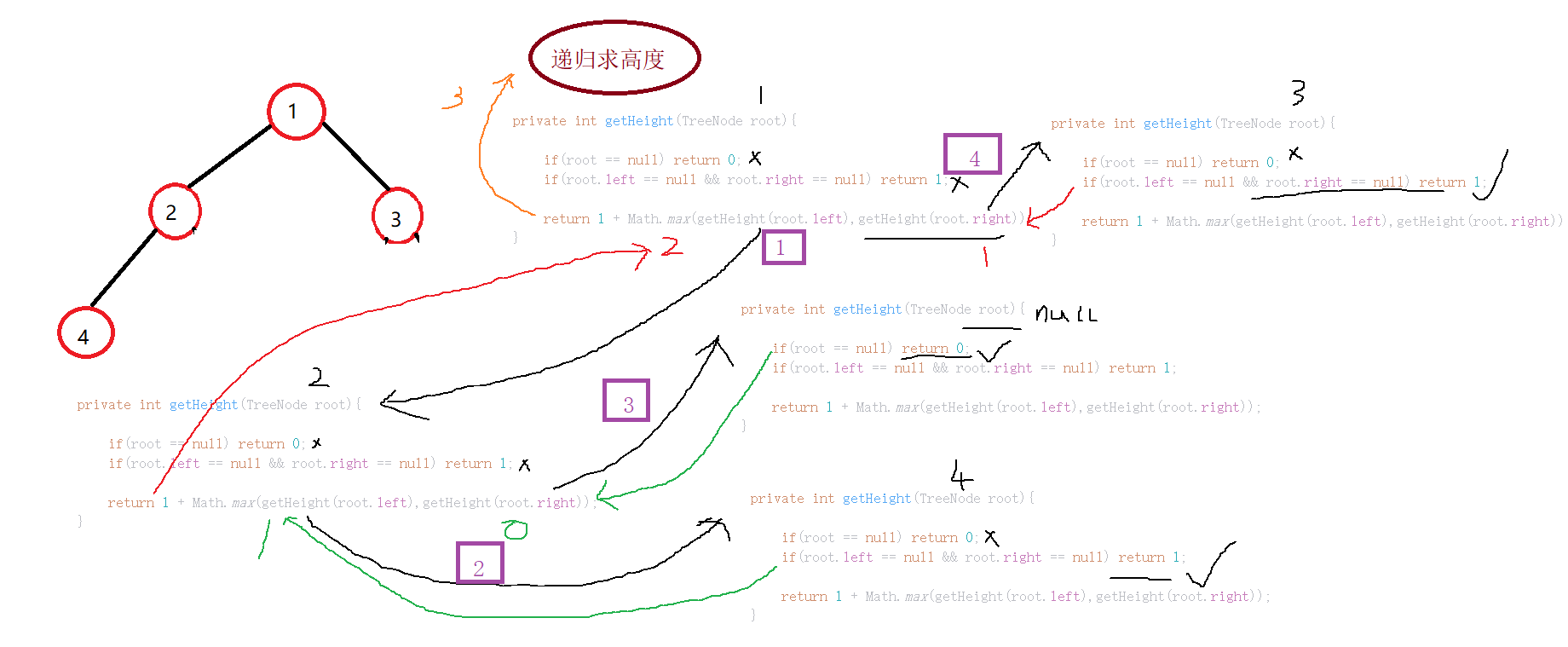
递归实现：判断根节点是否为空，是返回0，判断根节点是否左右节点为空，是返回1，以上情况都不是，递归求左子树高度和右子树高度的最大值,再加上根节点的高度。

    private int getHeight(TreeNode root){if(root == null) return 0;if(root.left == null && root.right == null) return 1;return 1 + Math.max(getHeight(root.left),getHeight(root.right));}//求二叉树的深度public int getHeight(){return getHeight(root);}   

    public static void main3(String[] args) {BinaryTree b = new BinaryTree();b.createBinaryTree(new int[]{1,2,3,4});System.out.println("二叉树的高度：" + b.getHeight());}

2.5 判断是否是完全二叉树

解法一：使用队列，按照层序遍历的方式入队列和出队列，直到循环结束，判断队列中的值，如果存在非null值，说明不是完全二叉树。

 public boolean isCompleteBinaryTree1(TreeNode root){//空树是完全二叉树if(root == null) return true;if(root.left == null && root.right == null) return true;//1.使用队列，加入根节点Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);TreeNode cur = root;//2.第一层循环while(null != cur){int size = queue.size();//第二层循环while(size-- != 0){cur = queue.poll();if(cur != null) {queue.offer(cur.left);queue.offer(cur.right);}}}//3.将队列元素全部弹出while(!queue.isEmpty()){if(queue.poll() != null)return false;}return true;}

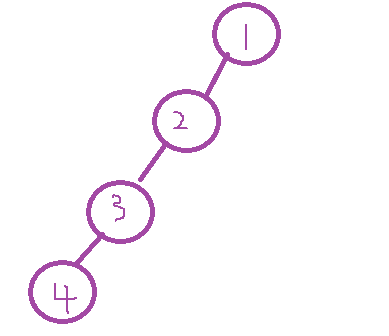
public static void main(String[] args) {TreeNode node1 =new TreeNode(1);TreeNode node2 =new TreeNode(1);TreeNode node3 =new TreeNode(1);TreeNode node4 =new TreeNode(1);node1.left = node2;node2.left = node3;node3.left = node4;//非完全二叉树BinaryTree b = new BinaryTree();System.out.println(b.isCompleteBinaryTree(node1));}

    public static void main(String[] args) {TreeNode node1 =new TreeNode(1);TreeNode node2 =new TreeNode(1);TreeNode node3 =new TreeNode(1);TreeNode node4 =new TreeNode(1);node1.left = node2;node1.right = node3;node3.left = node4;//完全二叉树BinaryTree b = new BinaryTree();System.out.println(b.isCompleteBinaryTree(node1));}

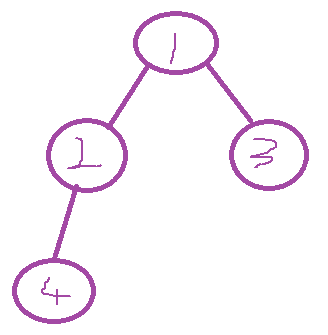
解法二：创建一个flat标记，默认所有的节点都是度为2的节点，发现不为2的节点，flat进行标记，此节点的下一节点不能有孩子节点，有孩子节点的不是完全二叉树。

 public boolean isCompleteBinaryTree2(TreeNode root){if(root == null) return true;//默认没有度不为2的节点boolean flat = false;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){TreeNode cur = queue.poll();//有右孩子，没左孩子，不是完全二叉树if(cur.left == null && cur.right != null){return false;}//度不为二的节点，进行标记if(flat && cur.left != null){return false;}if(cur.left == null || cur.right == null){flat = true;}//左右孩子不为空入队列if(cur.left != null) queue.offer(cur.left);if(cur.right != null) queue.offer((cur.right));}//以上情况都没有返回，说明是完全二叉树return true;}

解法三：使用标记点flat，默认加入队列的节点都不为空，如果发现为空的节点进行标记，标记后队列中不能存在不为null的节点。

    public boolean isCompleteBinaryTree3(TreeNode root){//空树是完全二叉树if(root == null) return true;if(root.left == null && root.right == null) return true;//1.使用队列，加入根节点Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);TreeNode cur;//队列中不存在null的节点boolean flat = false;//2.第一层循环while(!queue.isEmpty()){cur = queue.poll();if(cur == null){flat = true;//增加标记continue;//没有左右孩子节点不需要添加，直接到下一层循环}//队列中存在null，后面不能存在不为null的节点if(flat && cur != null){return false;}queue.offer(cur.left);queue.offer(cur.right);}return true;}

3.二叉树OJ题

3.1 判断两颗二叉树是否相等

相同的树

解法一：递归实现，先判断根节点，后判断左子树或右子树每一个节点的值都相等。

class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {//1，根节点一个为空，一个不为空if(p != null && q == null) return false;if(p == null && q != null) return false;//2.根节点都为空if(q == null && p == null) return true;//3.根节点不为空，节点值一样，左子树和右子树一样return (q.val == p.val) && isSameTree(p.left,q.left) && isSameTree(q.right,p.right);}
}

解法二： 非递归，按照中序遍历的方式将所有的节点值加入到ArrayList中，然后判断两棵二叉树所有节点值是否相同。

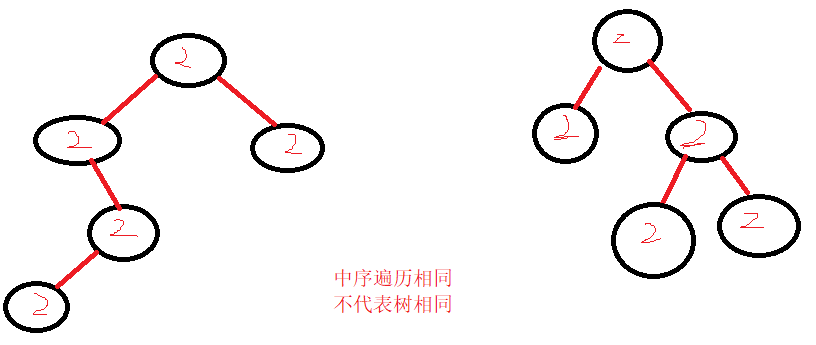
class Solution {private List<Integer> inOrderAdd(TreeNode root){//创建一个顺序表List<Integer> list = new ArrayList<>();//临时节点TreeNode tem = null;while(root != null){//左孩子节点不为空if(root.left != null){//将左孩子节点赋值给临时引用tem = root.left;//通过循环找到左子树最右边的节点，//将该节点的right赋值为根节点，方便后续回退到根节点while(tem.right != null && tem.right != root){tem = tem.right;}//1.找到左子树最右边的节点，需要赋值该节点的right为根节点//并让根节点赋值为左孩子节点if(tem.right == null){//添加0是因为特殊情况下，结构不同但是中序遍历添加的节点值一样//导致不同的树List一样返回true，因此需要添加标记，如果是一样的//添加的null的位置也是一样的list.add(null);tem.right = root;root = root.left;}//2.左子树没有右孩子节点或者左子树只有一个节点，此时需要将节点//值添加，将回退的right设置为null，并回根节点else{list.add(root.val);tem.right = null;root = root.right;}}//添加节点值，赋值右孩子节点,else{//添加根节点list.add(root.val);//赋值右孩子root = root.right;}}return list;}public boolean isSameTree(TreeNode p, TreeNode q) {return inOrderAdd(p).equals(inOrderAdd(q));}
}

3.2 判断子树

另一颗树的子树

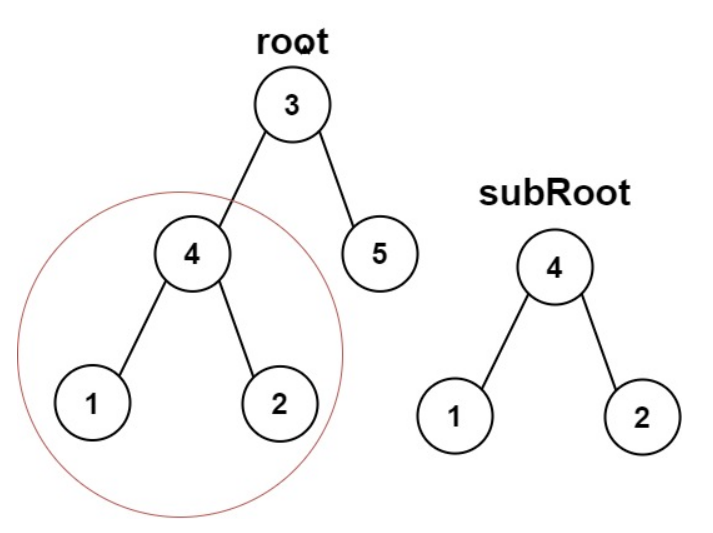
class Solution {public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null) return false;//父树为空，没有子树if(subRoot == null) return true;//子树为空，返回truereturn isSubtree(root.left,subRoot) || //递归判断左子树和右子数isSubtree(root.right,subRoot) ||isSame(root,subRoot); //当前的树}//判断两棵树是否相等public boolean isSame(TreeNode p,TreeNode q ){if(q == null && p == null) return true;if(q == null || p == null) return false;return (q.val == p.val && isSame(q.left,p.left) && isSame(q.right,p.right));}
}

3.3 反转二叉树

反转二叉树

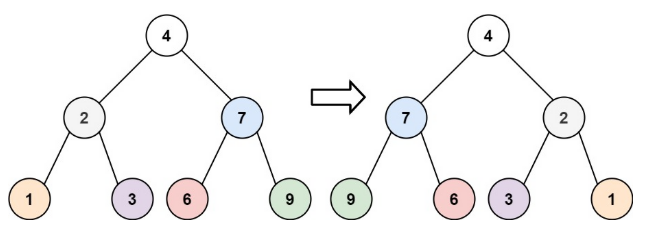
class Solution {public TreeNode invertTree(TreeNode root) {//处理没有节点和只有一个节点的情况if(root == null) return root;if(root.left == null && root.right == null) return root;//反转左树TreeNode lt = invertTree(root.left);//反转右树TreeNode rt = invertTree(root.right);//交换左右子树root.left = rt;root.right = lt;return root;}
}

3.4 判断平衡二叉树

平衡二叉树

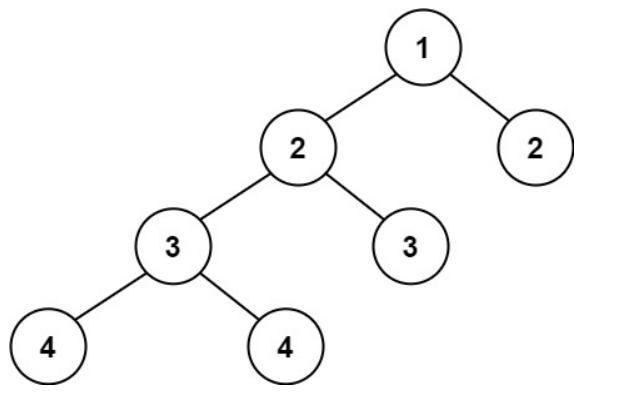
class Solution {public boolean isBalanced(TreeNode root) {if(root == null) return true;if(root.left == null && root.right == null) return true;return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) &&isBalanced(root.right);}//获取树的高度public int height(TreeNode root){if(root == null) return 0;if(root.left == null && root.right == null) return 1;return Math.max(height(root.left),height(root.right)) + 1;}
}

3.5 对称二叉树

对称二叉树

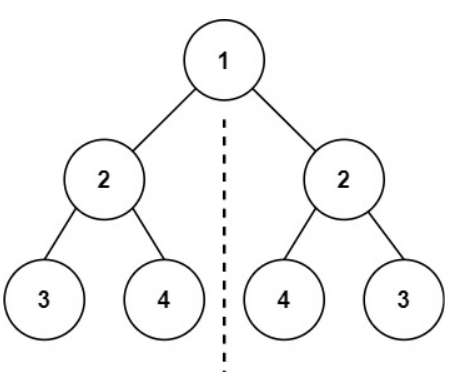
class Solution {public boolean isSymmetric(TreeNode root) {//空节点if(root == null) return true;//一个节点if(root.left == null && root.right == null) return true;//左孩子或者右孩子一个为空if(root.left == null || root.right == null) return false;//递归左右子树return  isSymmetric(root.left,root.right);   }public boolean isSymmetric(TreeNode l,TreeNode r) {//左右子树为空if(l == null && r == null) return true;//左右子树有一棵为空if(l == null || r == null) return false;//判断根节点值，递归左右子树return  l.val == r.val && isSymmetric(l.left,r.right) &&isSymmetric(l.right,r.left);}
}

3.6 二叉树的遍历

输入一个先序遍历的字符串，通过该字符串创建二叉树后中序遍历字符串。

例如：‘#’表示的是空节点，创建的二叉树如下

输入：abc##de#g##f###

输出：c b e g d f a

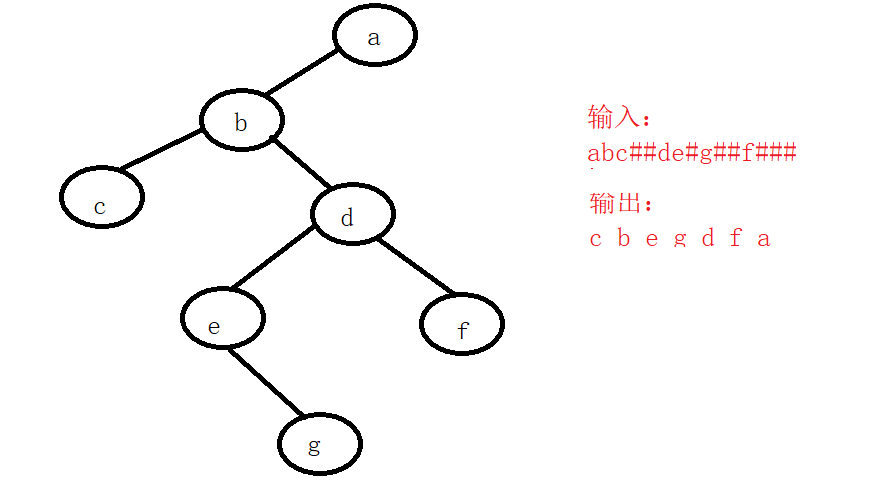
解决方法：使用递归函数创建二叉树，先创建根节点，后创建左子树和右子树，创建好后中序遍历

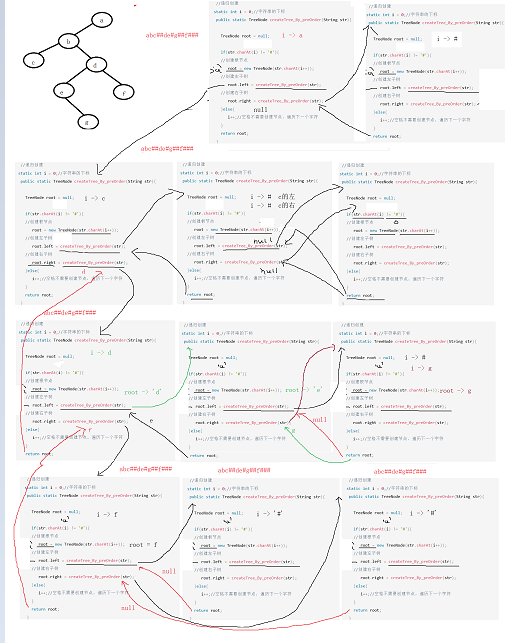
import java.util.Scanner;public class Main {//树节点类static class TreeNode{TreeNode left;TreeNode right;char val;public TreeNode(char val){this.val = val;}}//递归创建static int i = 0;//字符串的下标public static TreeNode createTree_By_preOrder(String str){TreeNode root = null;if(str.charAt(i) != '#'){//创建根节点root = new TreeNode(str.charAt(i++));//创建左子树root.left = createTree_By_preOrder(str);//创建右子树root.right = createTree_By_preOrder(str);}else{i++;//空格不需要创建节点，遍历下一个字符}return root;}
//中序遍历public static void inOrder(TreeNode root){if(root == null) return;if(root.left == null && root.right == null){System.out.print(root.val + " ");return;}//左 根 右inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}public static void main(String[] args) {//读入字符串Scanner in = new Scanner(System.in);while(in.hasNextLine()){String str = in.nextLine();TreeNode root = createTree_By_preOrder(str);inOrder(root);}}
}

3.7 两个树节点的的最小祖先节点

公共最小祖先节点

解法一：
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//两个节点其中一个是根节点if(p == root || q == root) return root;//一个节点在左子树，一个节点在右子树if (find(root.right,p) && find(root.left,q)) return root;if(!find(root.right,p) && !find(root.left,q)) return root;//两个节点都在一棵子树，递归该子树if(find(root.left,p) && find(root.left,q)) return lowestCommonAncestor(root.left,p,q);if(find(root.right,p) && find(root.right,q))return lowestCommonAncestor(root.right,p,q);//没有公共节点return null;}//查看p或q位于的位置：左子树或者右子树public boolean find(TreeNode root ,TreeNode t){if(root == null) return false;if(t == null) return true;return find(root.left,t) || find(root.right,t) || root.val == t.val;}
}

解法二：递归记录最小公共祖先
class Solution {//最小公共祖先TreeNode ancestor = null;//递归函数public boolean dps(TreeNode root, TreeNode p, TreeNode q) {//p,q，== root 或者 root == null if (root == null) return false;//递归dps:查看左子树或者右子树是否包含p或者qboolean lt = dps(root.left,p,q);boolean rt = dps(root.right,p,q);//lt和rt都为真或者都在一棵子树中，说明节点在树的两边，根节点为公共祖先if((lt && rt) || ((root.val == p.val || root.val == q.val) && (lt || rt))){ancestor = root;}//查找的节点是否在树中return lt || rt || (root.val == p.val || root.val == q.val); }//调用递归函数，返回最小公共祖先public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {this.dps(root,  p,  q);return this.ancestor;}
}

3.8 根据前序和中续遍历创建二叉树

前序遍历和中序遍历创建二叉树

class Solution {//查找根节点下标位置private int findIndex(int[] order,int inbegin,int inend,int target){for(int i = inbegin;i <= inend;i++){if(order[i] == target){return i;}}return -1;}//递归函数public TreeNode buildTree(int[] preorder, int[] inorder,int inbegin,int inend) {//结束条件if(inbegin > inend) return null;//创建根节点TreeNode root = new TreeNode(preorder[i]);//找到根节点在中序遍历的坐标，划分左右子树int index = findIndex(inorder,inbegin,inend,preorder[i++]);//创建左子树root.left = buildTree(preorder,inorder,inbegin,index -1);//创建右子树root.right = buildTree(preorder,inorder,index + 1,inend);//返回根节点return root;}int i = 0;//遍历preorderpublic TreeNode buildTree(int[] preorder, int[] inorder) {//调用递归函数创建return  buildTree(preorder,inorder,0,inorder.length - 1);}
}

3.9 中序遍历和后续遍历创建二叉树

中序遍历和后续遍历创建二叉树

解法一：划分区间创建
class Solution {private int findIndex(int[] inorder,int inbegin,int inend,int target){for(int i = inbegin;i <= inend;i++){if(inorder[i] == target){return i;}}return -1;}public TreeNode buildTree(int[] inorder, int[] postorder,int inbegin,int inend) {//结束条件if(inbegin > inend) return null;//创建根节点TreeNode root = new TreeNode(postorder[i]);//查找根节点索引int index = findIndex(inorder,inbegin,inend,postorder[i--]);//创建右子树root.right = buildTree(inorder,postorder,index + 1,inend);//创建左子树root.left = buildTree(inorder,postorder,inbegin,index -1);return root;}//后续遍历下标int i;public TreeNode buildTree(int[] inorder, int[] postorder) {i = postorder.length -1;return buildTree(inorder,postorder,0,inorder.length -1);}
}

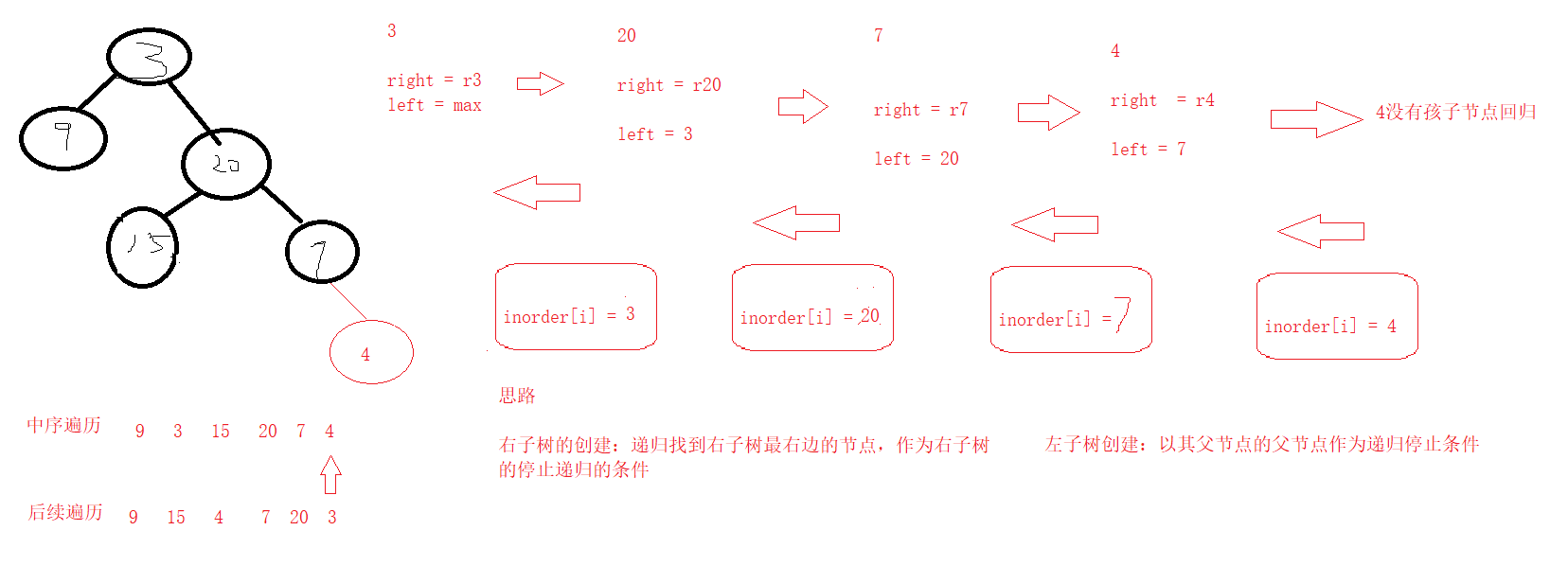
解法二：从后往前遍历，找到右子树创建的终止条件和左子树创建的终止条件
class Solution {public  static TreeNode createTree_By_post_and_in(int[] inorder,int[] postorder,int stop){//数组遍历完成if(in < 0) return null;//左子树的终止条件和右子树的终止条件if(inorder[in] == stop){in--;return null;}//创建根节点TreeNode root = new TreeNode(postorder[post--]);//创建右子树:递归到最右边的节点，找到root.val = inorder[in] 停止递归root.right = createTree_By_post_and_in(inorder,postorder,root.val);//创建左子树:递归到左子树的父亲节点为终止条件，inorder[in] = stoproot.left = createTree_By_post_and_in(inorder,postorder,stop);//返回return root;}static int in = 0,post = 0;public TreeNode buildTree(int[] inorder, int[] postorder) {//从后往前遍历数组in = inorder.length - 1;post = postorder.length - 1;return createTree_By_post_and_in(inorder,postorder,Integer.MAX_VALUE);}
}

3.10 二叉树转变为指定形式的字符串

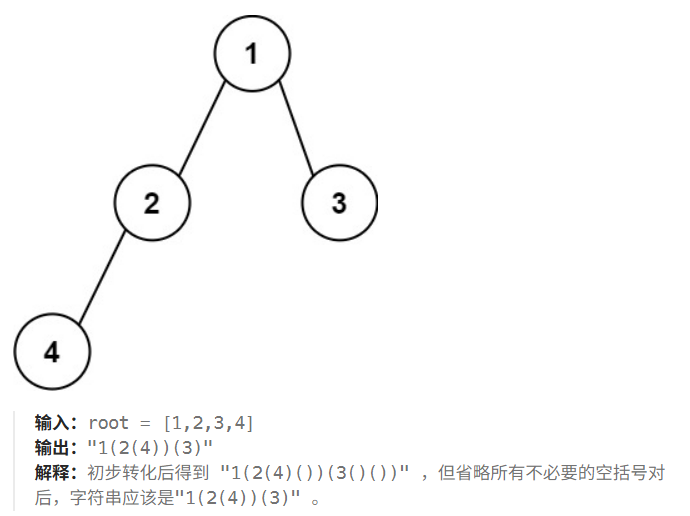
按照前序遍历的方式将二叉树转变为由括号和数字组成的字符串。根据二叉树创建字符串

class Solution {//树节点类static class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}public TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}
//递归函数public String tree2str(TreeNode root){//根节点为空，返回空字符串if(root == null) return "";//只有一个节点if(root.left == null && root.right == null){return Integer.toString(root.val);}//拼接StringBuilder st = new StringBuilder();//根节点st.append(root.val);//1.左子树为空if(root.left == null){//1.1右子树也为空if(root.right == null){return "";//1.2右子树不为空}else{st.append("()");//区分左子树//拼接右子树st.append("(");st.append(tree2str(root.right));st.append(")");}//2.左子树不为空}else{//2.1右子树为空if(root.right == null){//拼接左子树st.append("(");st.append(tree2str1(root.left));st.append(")");//2.2 右子树不为空}else{//拼接左子树st.append("(");st.append(tree2str(root.left));st.append(")");//拼接右子树st.append("(");st.append(tree2str(root.right));st.append(")");}}//返回return st.toString();}public static void main(String[] args) {TreeNode n1 = new TreeNode(1);TreeNode n2 = new TreeNode(2);TreeNode n3 = new TreeNode(3);TreeNode n4 = new TreeNode(4);n1.left = n2;     //        1n2.right = n3;    //   2    n3.left = n4;     //     3//  4Solution s = new Solution();System.out.println(s.tree2str(n1));}
}

3.10 二叉树的的遍历（非递归）

1.前序遍历
非递归的前序遍历需要利用栈来存储数据，由于栈是一种先进后出的数据结构，而前序遍历是根，左，右的方式打印，因此入栈的时候先入右边节点，再入左边节点，打印就可以按照根，左，右的方式打印。

class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();if(root == null) return list;stack.push(root);while(!stack.empty()){TreeNode cur = stack.pop();list.add(cur.val);if(cur.right != null){stack.push(cur.right);}if(cur.left != null){stack.push(cur.left);}}return list;}
}

2.中序遍历

入栈：依次加入左边节点直到cur为null

出栈：栈顶元素出栈，查看该右节点是否为空，不为空入栈

class Solution {public List<Integer> inorderTraversal(TreeNode root) {if(root == null) return new LinkedList<Integer>();List<Integer> list = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;stack.push(root);while(!stack.empty() || cur.left != null){while(cur.left != null){stack.push(cur.left);cur = cur.left;}TreeNode t = stack.pop();list.add(t.val);if(t.right != null){cur = t.right;stack.push(t.right);}}return list;}
}

3.后续遍历

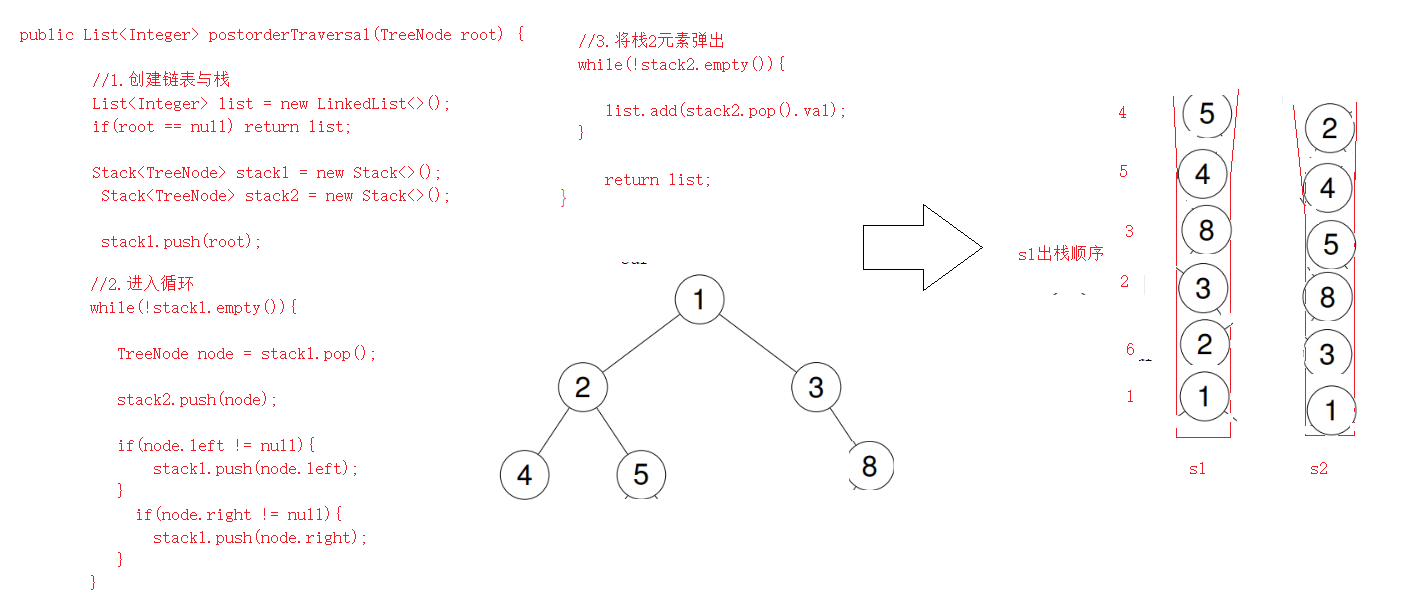
class Solution {public List<Integer> postorderTraversal(TreeNode root) {if(root == null) return new LinkedList<Integer>();Stack<TreeNode> s1 = new Stack<>();Stack<TreeNode> s2 = new Stack<>();List<Integer> list = new LinkedList<>();s1.push(root);while(!s1.empty()){TreeNode cur = s1.pop();s2.push(cur);if(cur.left != null){s1.push(cur.left);}if(cur.right != null){s1.push(cur.right);}}while(s2.empty() != true){list.add(s2.pop().val);}return list;}
}