[GESP202406 五级] 黑白格

视频讲解：[GESP202406 五级] 黑白格-信息学奥赛GESP等级考试真题解析

一、原题

题目描述

小杨有一个 n 行 m 列的网格图，其中每个格子要么是白色，要么是黑色。

小杨想知道至少包含 k 个黑色格子的最小子矩形包含了多少个格子。

输入格式

第一行包含三个正整数 n,m,k，含义如题面所示。

之后 n 行，每行⼀个长度为 m 的 01 串，代表网格图第 i 行格子的颜色，如果为 0，则对应格子为白色，否则为黑色。

输出格式

输出一个整数，代表至少包含 k 个黑色格子的最小子矩形包含格子的数量，如果不存在则输出 0。

输入输出样例

输入 #1

4 5 5
00000
01111
00011
00011

输出 #1

6

说明/提示

样例解释

对于样例 1，假设 (i,j) 代表第 i 行第 j 列，至少包含 5 个黑色格子的最小子矩形的四个顶点为 (2,4)，(2,5)，(4,4)，(4,5)，共包含 6 个格子。

数据范围

对于全部数据，保证有 1≤n,m≤100，1≤k≤n×m。

子任务编号	得分	n,m
1	20	≤10
2	40	n=1，1≤m≤100
3	40	≤100

二、做题思路

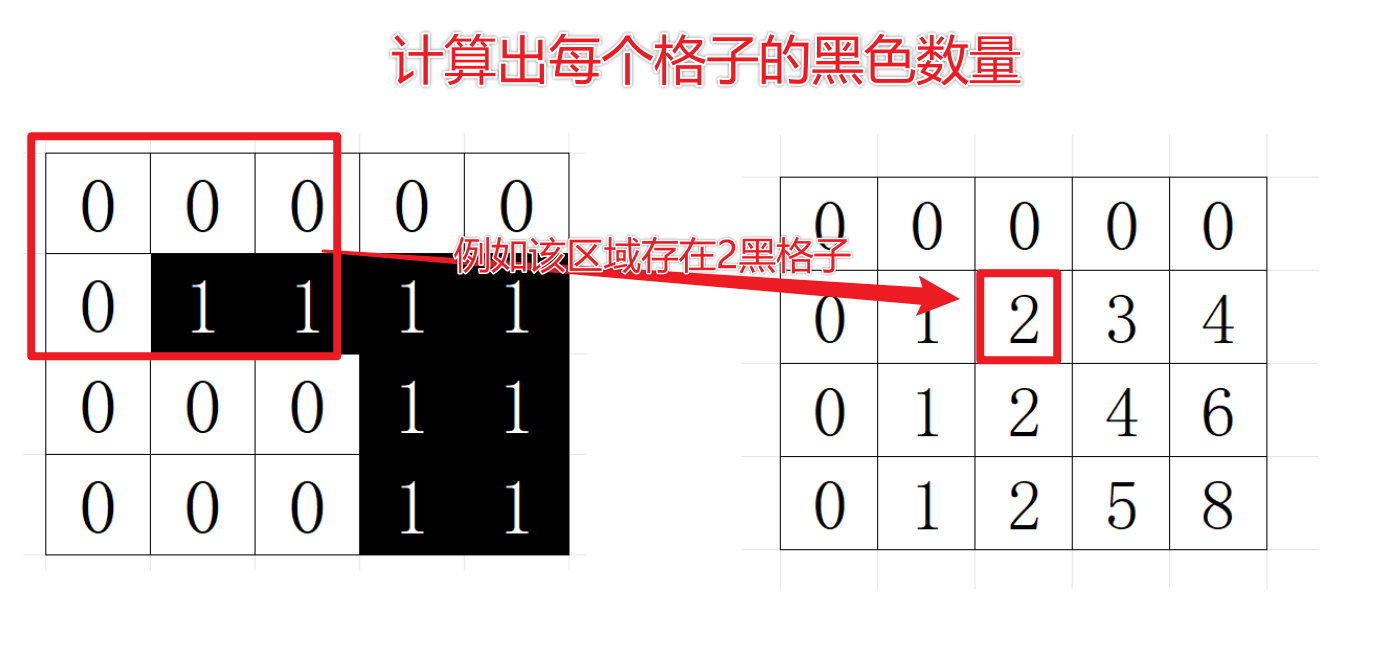
1)填充数据，同时计算每个格子的前缀和

 #include<bits/stdc++.h>
using namespace std;
int sum[110][110];
void cal(int i,int j,int x){sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+x;
}
int main() {//1)填充数据//1.1)确定矩阵大小n*m,条件kint n,m,k;cin>>n>>m>>k;//1.2)填充矩阵的情况for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){char x;cin>>x;//2)计算当前坐标的黑格子数量cal(i,j,x-'0');}}
}

2)枚举所有子矩阵

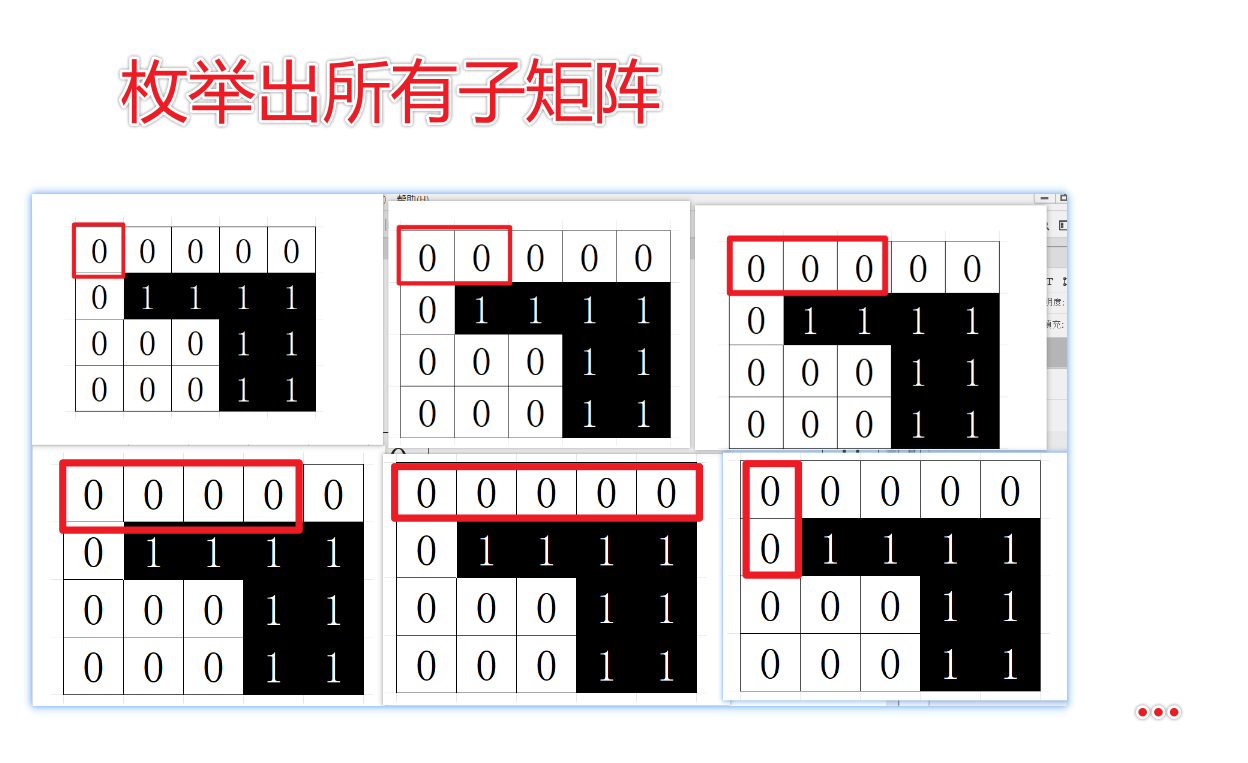
//3)枚举所有子矩阵的情况
int minn=INT_MAX; 
//3.1)枚举左上顶点 
for(int left_i=1;left_i<=n;left_i++){for(int left_j=1;left_j<=m;left_j++){//3.2)枚举右下顶点 for(int right_i=1;right_i<=n;right_i++){for(int right_j=1;right_j<=m;right_j++){}}}
}

3)计算当前矩阵黑格子数量，比较找出最小值

 //3)枚举所有子矩阵的情况
int minn=INT_MAX; 
//3.1)枚举左上顶点 
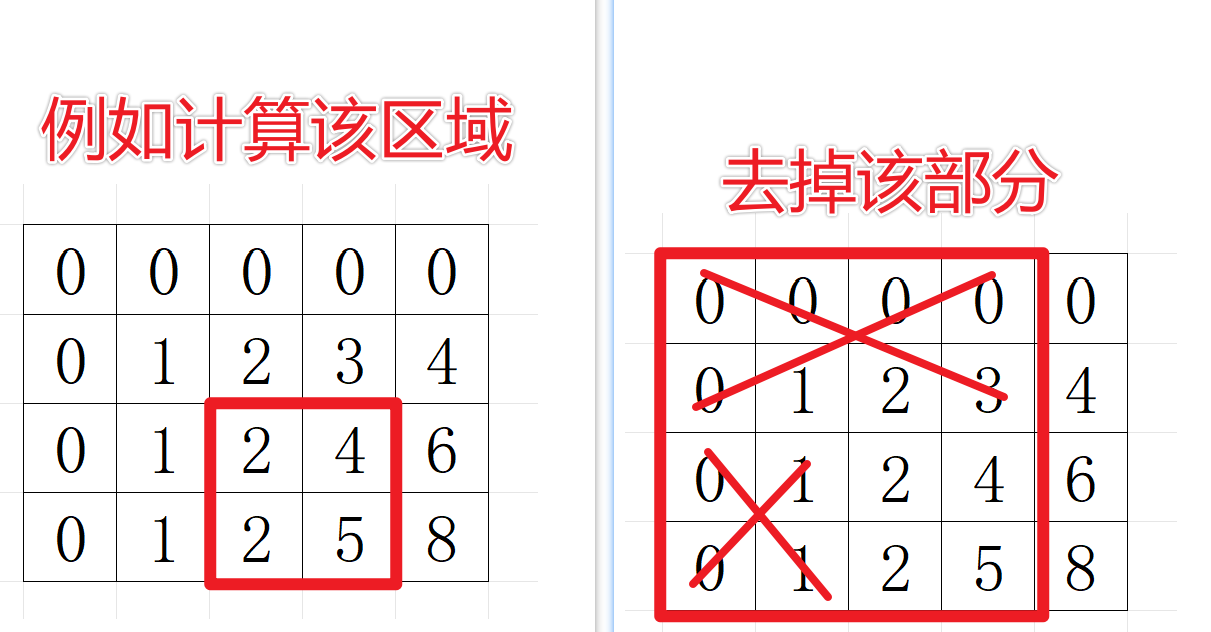
for(int left_i=1;left_i<=n;left_i++){for(int left_j=1;left_j<=m;left_j++){//3.2)枚举右下顶点 for(int right_i=1;right_i<=n;right_i++){for(int right_j=1;right_j<=m;right_j++){//4)计算是否条件，找出最小矩阵//4.1)计算当前区域的黑格子数量int now=sum[right_i][right_j]-(sum[left_i-1][right_j]+sum[right_i][left_j-1]-sum[left_i-1][left_j-1]);//4.2)符合条件就比较更新 最小面积if(now>=k){minn=min(  minn, (right_i-left_i+1)*(right_j-left_j+1)  );}}}}
}
//5)输出
cout<<(minn==INT_MAX ? 0 : minn);

三、答案

#include<bits/stdc++.h>
using namespace std;
int sum[110][110];
void cal(int i,int j,int x){sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+x;
}
int main() {//1)填充数据//1.1)确定矩阵大小n*m,条件kint n,m,k;cin>>n>>m>>k;//1.2)填充矩阵的情况for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){char x;cin>>x;//2)计算当前坐标的黑格子数量cal(i,j,x-'0');}}//3)枚举所有子矩阵的情况int minn=INT_MAX; //3.1)枚举左上顶点 for(int left_i=1;left_i<=n;left_i++){for(int left_j=1;left_j<=m;left_j++){//3.2)枚举右下顶点 for(int right_i=1;right_i<=n;right_i++){for(int right_j=1;right_j<=m;right_j++){//4)计算是否条件，找出最小矩阵//4.1)计算当前区域的黑格子数量int now=sum[right_i][right_j]-(sum[left_i-1][right_j]+sum[right_i][left_j-1]-sum[left_i-1][left_j-1]);//4.2)符合条件就比较更新 最小面积if(now>=k){minn=min(  minn, (right_i-left_i+1)*(right_j-left_j+1)  );}}}}}//5)输出cout<<(minn==INT_MAX ? 0 : minn);
}