《强化学习数学原理》学习笔记9——值迭代算法
一、值迭代算法是什么
值迭代(Value Iteration)是强化学习里求解贝尔曼最优方程的经典算法,核心是通过不断迭代更新状态价值,最终得到最优状态价值和最优策略。
(一)迭代更新的数学基础
值迭代的迭代公式为,见博文式(2):
vk+1=maxπ∈Π(rπ+γPπvk),k=0,1,2,…(1)v_{k + 1} = \max_{\pi \in \Pi} (r_{\pi} + \gamma P_{\pi} v_k), \quad k = 0, 1, 2, \dots \tag{1} vk+1=π∈Πmax(rπ+γPπvk),k=0,1,2,…(1)
这里 vkv_kvk 是第 kkk 次迭代的状态价值向量,rπr_{\pi}rπ 是策略 π\piπ 下的即时奖励向量,PπP_{\pi}Pπ 是策略 π\piπ 对应的状态转移矩阵,γ\gammaγ 是折扣因子。
从压缩映射的角度看,因为 γ<1\gamma < 1γ<1,对于任意初始状态价值 v0,v1v_0, v_1v0,v1,当 k→∞k \to \inftyk→∞ 时,∥vk+1−vk∥\|v_{k + 1} - v_k\|∥vk+1−vk∥ 会指数级收敛到 0。不过,仅 ∥vk+1−vk∥→0\|v_{k + 1} - v_k\| \to 0∥vk+1−vk∥→0 还不够证明 {vk}\{v_k\}{vk} 收敛,需进一步分析 m>nm > nm>n 时的 ∥vm−vn∥\|v_m - v_n\|∥vm−vn∥。
把 ∥vm−vn∥\|v_m - v_n\|∥vm−vn∥ 拆分为:
∥vm−vn∥=∥vm−vm−1+vm−1−⋯−vn+1+vn+1−vn∥(2)\|v_m - v_n\| = \|v_m - v_{m - 1} + v_{m - 1} - \cdots - v_{n + 1} + v_{n + 1} - v_n\| \tag{2} ∥vm−vn∥=∥vm−vm−1+vm−1−⋯−vn+1+vn+1−vn∥(2)
根据范数的三角不等式(∥a+b∥≤∥a∥+∥b∥\|a + b\| \leq \|a\| + \|b\|∥a+b∥≤∥a∥+∥b∥),上式可推出:
∥vm−vn∥≤∥vm−vm−1∥+⋯+∥vn+1−vn∥(3)\|v_m - v_n\| \leq \|v_m - v_{m - 1}\| + \cdots + \|v_{n + 1} - v_n\| \tag{3} ∥vm−vn∥≤∥vm−vm−1∥+⋯+∥vn+1−vn∥(3)
又因为 ∥vk+1−vk∥≤γk∥v1−v0∥\|v_{k + 1} - v_k\| \leq \gamma^k \|v_1 - v_0\|∥vk+1−vk∥≤γk∥v1−v0∥,代入上式得:
∥vm−vn∥≤γm−1∥v1−v0∥+⋯+γn∥v1−v0∥=γn(γm−1−n+⋯+1)∥v1−v0∥≤γn(1+γ+⋯+γm−1−n+γm−n+⋯)∥v1−v0∥\begin{align*} \|v_m - v_n\| &\leq \gamma^{m - 1} \|v_1 - v_0\| + \cdots + \gamma^n \|v_1 - v_0\| \\ &= \gamma^n (\gamma^{m - 1 - n} + \cdots + 1) \|v_1 - v_0\| \\ &\leq \gamma^n (1 + \gamma + \cdots + \gamma^{m-1-n} + \gamma^{m-n} + \cdots) \|v_1 - v_0\| \tag{4} \end{align*} ∥vm−vn∥≤γm−1∥v1−v0∥+⋯+γn∥v1−v0∥=γn(γm−1−n+⋯+1)∥v1−v0∥≤γn(1+γ+⋯+γm−1−n+γm−n+⋯)∥v1−v0∥(4)
等比数列 1+γ+γ2+⋯1 + \gamma + \gamma^2 + \cdots1+γ+γ2+⋯ 的和为 11−γ\frac{1}{1 - \gamma}1−γ1(因 γ<1\gamma < 1γ<1),所以:
∥vm−vn∥≤γn1−γ∥v1−v0∥(5)\|v_m - v_n\| \leq \frac{\gamma^n}{1 - \gamma} \|v_1 - v_0\| \tag{5} ∥vm−vn∥≤1−γγn∥v1−v0∥(5)
这表明,对任意 ε>0\varepsilon > 0ε>0,总能找到 NNN,当 m,n>Nm, n > Nm,n>N 时,∥vm−vn∥<ε\|v_m - v_n\| < \varepsilon∥vm−vn∥<ε,即 {vk}\{v_k\}{vk} 是柯西序列,必然收敛到极限 v∗=limk→∞vkv^* = \lim_{k \to \infty} v_kv∗=limk→∞vk,v∗v^*v∗ 就是最优状态价值。
(二)迭代的两步操作
值迭代算法中,每次迭代分为两个步骤:
- 策略更新步:在第 kkk 次迭代,根据当前状态价值 vkv_kvk,找到能最大化 rπ+γPπvkr_{\pi} + \gamma P_{\pi} v_krπ+γPπvk 的策略 πk+1\pi_{k + 1}πk+1,即:
πk+1=argmaxπ(rπ+γPπvk)(6)\pi_{k + 1} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_k) \tag{6} πk+1=argπmax(rπ+γPπvk)(6)
对于每个状态 sss,要找到使 ∑aπ(a∣s)(∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′))\sum_{a} \pi(a|s) \left( \sum_{r} p(r|s, a)r + \gamma \sum_{s'} p(s'|s, a)v_k(s') \right)∑aπ(a∣s)(∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′)) 最大的策略,最优策略是确定性贪婪策略:
πk+1(a∣s)={1,a=ak∗(s)0,a≠ak∗(s)(7)\pi_{k + 1}(a|s) = \begin{cases} 1, & a = a_k^*(s) \\ 0, & a \neq a_k^*(s) \tag{7} \end{cases} πk+1(a∣s)={1,0,a=ak∗(s)a=ak∗(s)(7)
其中 ak∗(s)=argmaxaqk(s,a)a_k^*(s) = \arg\max_{a} q_k(s, a)ak∗(s)=argmaxaqk(s,a),qk(s,a)=∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′)q_k(s, a) = \sum_{r} p(r|s, a)r + \gamma \sum_{s'} p(s'|s, a)v_k(s')qk(s,a)=∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′)。若 ak∗(s)a_k^*(s)ak∗(s) 有多个解,也就是多个动作具有相同的最大动作价值,任选其一不影响算法收敛,这种选最大 qk(s,a)q_k(s, a)qk(s,a) 对应动作的策略就是贪婪策略。 - 价值更新步:用新策略 πk+1\pi_{k + 1}πk+1 计算新的状态价值 vk+1v_{k + 1}vk+1,公式为:
vk+1=rπk+1+γPπk+1vk(8)v_{k + 1} = r_{\pi_{k + 1}} + \gamma P_{\pi_{k + 1}} v_k \tag{8} vk+1=rπk+1+γPπk+1vk(8)
对每个状态 sss,有:
vk+1(s)=∑aπk+1(a∣s)(∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′))(9)v_{k + 1}(s) = \sum_{a} \pi_{k + 1}(a|s) \left( \sum_{r} p(r|s, a)r + \gamma \sum_{s'} p(s'|s, a)v_k(s') \right) \tag{9} vk+1(s)=a∑πk+1(a∣s)(r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vk(s′))(9)
将贪婪策略代入,可得 vk+1(s)=maxaqk(s,a)v_{k + 1}(s) = \max_{a} q_k(s, a)vk+1(s)=maxaqk(s,a)。
总结一下,值迭代步骤如下所示:
已知vk(s)→计算qk(s,a)→计算新策略πk+1(s)→由新策略得到新价值函数 vk+1(s)=maxaqk(s,a)已知v_k(s) \to 计算q_k(s, a) \to \text{计算新策略} \pi_{k+1}(s) \to \text{由新策略得到新价值函数 } v_{k+1}(s) = \max_a q_k(s, a)已知vk(s)→计算qk(s,a)→计算新策略πk+1(s)→由新策略得到新价值函数 vk+1(s)=maxaqk(s,a)
参考书中的伪代码:

三、直观示例:网格世界中的值迭代
以书中一个 2×22 \times 22×2 网格(含一个禁止区域)为例,目标区域是 s4s_4s4(如下图所示),奖励设置为:边界和禁止区域奖励 rboundary=rforbidden=−1r_{\text{boundary}} = r_{\text{forbidden}} = -1rboundary=rforbidden=−1,目标区域奖励 rtarget=1r_{\text{target}} = 1rtarget=1,折扣率 γ=0.9\gamma = 0.9γ=0.9。
(一) 初始化
首先,我们需要对初始状态价值进行设定。在这个示例中,为了简化计算且不失一般性,我们令初始状态价值 v0(s1)=v0(s2)=v0(s3)=v0(s4)=0v_0(s_1) = v_0(s_2) = v_0(s_3) = v_0(s_4) = 0v0(s1)=v0(s2)=v0(s3)=v0(s4)=0。这就是给算法一个起始点,让它从这里开始探索各个状态的价值。
同时设定五个动作:a1,a2,a3,a4,a5a_1,a_2,a_3,a_4,a_5a1,a2,a3,a4,a5 分别表示向上,右,下,左,原地不动。
(二)第 k=0k = 0k=0 次迭代
1. 计算 qqq 值
在已确定每一个状态选择的动作条件下,动作价值就等于此时的状态价值,也就是说此时:
q(a,s)=v(s)=rπ+γPπv(s)(10)q(a,s) = v(s) = r_\pi + \gamma P_{\pi} v(s) \tag{10} q(a,s)=v(s)=rπ+γPπv(s)(10)
根据每个状态 - 动作对的 qqq 值计算公式,计算得到 q−tabelq-tabelq−tabel :
| q-table | a1a_1a1 | a2a_2a2 | a3a_3a3 | a4a_4a4 | a5a_5a5 |
|---|---|---|---|---|---|
| s1s_1s1 | −1+γv(s1)-1 + \gamma v(s_1)−1+γv(s1) | −1+γv(s2)-1 + \gamma v(s_2)−1+γv(s2) | 0+γv(s3)0 + \gamma v(s_3)0+γv(s3) | −1+γv(s1)-1 + \gamma v(s_1)−1+γv(s1) | 0+γv(s1)0 + \gamma v(s_1)0+γv(s1) |
| s2s_2s2 | −1+γv(s2)-1 + \gamma v(s_2)−1+γv(s2) | −1+γv(s2)-1 + \gamma v(s_2)−1+γv(s2) | 1+γv(s4)1 + \gamma v(s_4)1+γv(s4) | 0+γv(s1)0 + \gamma v(s_1)0+γv(s1) | −1+γv(s2)-1 + \gamma v(s_2)−1+γv(s2) |
| s3s_3s3 | 0+γv(s1)0 + \gamma v(s_1)0+γv(s1) | 1+γv(s4)1 + \gamma v(s_4)1+γv(s4) | −1+γv(s3)-1 + \gamma v(s_3)−1+γv(s3) | −1+γv(s3)-1 + \gamma v(s_3)−1+γv(s3) | 0+γv(s3)0 + \gamma v(s_3)0+γv(s3) |
| s4s_4s4 | −1+γv(s2)-1 + \gamma v(s_2)−1+γv(s2) | −1+γv(s4)-1 + \gamma v(s_4)−1+γv(s4) | −1+γv(s4)-1 + \gamma v(s_4)−1+γv(s4) | 0+γv(s3)0 + \gamma v(s_3)0+γv(s3) | 1+γv(s4)1 + \gamma v(s_4)1+γv(s4) |
现在,把初始的状态价值 v0(si)=0v_0(s_i) = 0v0(si)=0 代入这些公式,就可以计算出各状态 - 动作对的 qqq 值,结果如下表所示,每一行中标粗的:
| q-table | a1a_1a1 | a2a_2a2 | a3a_3a3 | a4a_4a4 | a5a_5a5 |
|---|---|---|---|---|---|
| s1s_1s1 | −1-1−1 | −1-1−1 | 000 | −1-1−1 | 000 |
| s2s_2s2 | −1-1−1 | −1-1−1 | 111 | 000 | −1-1−1 |
| s3s_3s3 | 000 | 111 | −1-1−1 | −1-1−1 | 000 |
| s4s_4s4 | −1-1−1 | −1-1−1 | −1-1−1 | 000 | 111 |
2. 策略更新
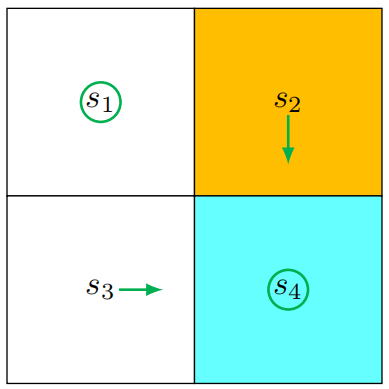
策略更新的原则是为每个状态选择 qqq 值最大的动作。观察表中每一行的 qqq 值,我们依据贪婪原则得到此时的最优策略 π1\pi_1π1:π1(a5∣s1)=1\pi_1(a_5|s_1) = 1π1(a5∣s1)=1(状态 s1s_1s1 选择动作 a5a_5a5)、π1(a3∣s2)=1\pi_1(a_3|s_2) = 1π1(a3∣s2)=1(状态 s2s_2s2 选择动作 a3a_3a3)、π1(a2∣s3)=1\pi_1(a_2|s_3) = 1π1(a2∣s3)=1(状态 s3s_3s3 选择动作 a2a_2a2)、π1(a5∣s4)=1\pi_1(a_5|s_4) = 1π1(a5∣s4)=1(状态 s4s_4s4 选择动作 a5a_5a5)。
把这个策略可视化(如下图所示),我们能发现,在状态 s1s_1s1 处,算法选择了静止的动作。此时这个策略并不是最优的,不过值得注意的是,状态 s1s_1s1 下动作 a5a_5a5 和 a3a_3a3 的 qqq 值是相同的,所以在实际中可以随机选择其中一个动作(本例选 a5a_5a5)。
3. 价值更新
价值更新是将每个状态的 vvv 值更新为该状态下最大的 qqq 值。从表中找到每个状态的最大 qqq 值,更新后得到:v1(s1)=0v_1(s_1) = 0v1(s1)=0,v1(s2)=1v_1(s_2) = 1v1(s2)=1,v1(s3)=1v_1(s_3) = 1v1(s3)=1,v1(s4)=1v_1(s_4) = 1v1(s4)=1。
(三)第 k=1k = 1k=1 次迭代
1. 计算 qqq 值
现在,我们把上一次迭代得到的状态价值 v1(si)v_1(s_i)v1(si) 代入 qqq 值计算公式(表 4.1),得到新的 qqq 值,结果如下表所示:
| q-table | a1a_1a1 | a2a_2a2 | a3a_3a3 | a4a_4a4 | a5a_5a5 |
|---|---|---|---|---|---|
| s1s_1s1 | −1+γ×0-1 + \gamma \times 0−1+γ×0 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | 0+γ×10 + \gamma \times 10+γ×1 | −1+γ×0-1 + \gamma \times 0−1+γ×0 | 0+γ×00 + \gamma \times 00+γ×0 |
| s2s_2s2 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | 1+γ×11 + \gamma \times 11+γ×1 | 0+γ×00 + \gamma \times 00+γ×0 | −1+γ×1-1 + \gamma \times 1−1+γ×1 |
| s3s_3s3 | 0+γ×00 + \gamma \times 00+γ×0 | 1+γ×11 + \gamma \times 11+γ×1 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | 0+γ×10 + \gamma \times 10+γ×1 |
| s4s_4s4 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | −1+γ×1-1 + \gamma \times 1−1+γ×1 | 0+γ×10 + \gamma \times 10+γ×1 | 1+γ×11 + \gamma \times 11+γ×1 |
2. 策略更新
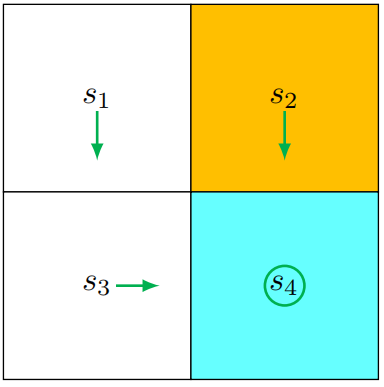
同样按照选择各状态下最大 qqq 值对应动作的原则,得到策略 π2\pi_2π2:π2(a3∣s1)=1\pi_2(a_3|s_1) = 1π2(a3∣s1)=1、π2(a3∣s2)=1\pi_2(a_3|s_2) = 1π2(a3∣s2)=1、π2(a2∣s3)=1\pi_2(a_2|s_3) = 1π2(a2∣s3)=1、π2(a5∣s4)=1\pi_2(a_5|s_4) = 1π2(a5∣s4)=1。将这个策略可视化(如下图所示),可以看到此时的策略已经是最优的了。
3. 价值更新
更新状态价值为:v2(s1)=γ×1v_2(s_1) = \gamma \times 1v2(s1)=γ×1,v2(s2)=1+γ×1v_2(s_2) = 1 + \gamma \times 1v2(s2)=1+γ×1,v2(s3)=1+γ×1v_2(s_3) = 1 + \gamma \times 1v2(s3)=1+γ×1,v2(s4)=1+γ×1v_2(s_4) = 1 + \gamma \times 1v2(s4)=1+γ×1。
(四)后续迭代
在这个简单的示例中,仅仅经过两次迭代就得到了最优策略。但在更复杂的场景中,我们需要进行更多次的迭代,直到状态价值 vkv_kvk 收敛,也就是当 ∥vk+1−vk∥\|v_{k + 1} - v_k\|∥vk+1−vk∥ 小于我们预先设定的阈值时,才停止迭代。
通过这个示例,可以清晰地看到价值迭代算法是如何通过不断更新 qqq 值、策略和状态价值,最终找到最优策略的。
四、总结
值迭代算法通过“策略更新 - 价值更新”的迭代过程,利用压缩映射的收敛性,能从任意初始状态价值出发,逐步逼近最优状态价值和最优策略,且在简单场景下收敛速度较快,是理解强化学习中策略与价值交互优化的基础方法。
