归一化处理1

归一化并不总是将样本分布转换到0-1区间。0-1区间转换是归一化的一种常见形式，但归一化本身是一个更广泛的概念，包含了多种将数据缩放至特定范围或分布的方法。

为了让你快速把握全貌，下表对比了三种主要的归一化方法及其输出区间。

方法类型	核心目标	典型输出区间	一个关键特点
Min-Max 归一化	将数据线性缩放至一个固定区间	[0, 1] 或 [-1, 1]	对原始数据的最大值和最小值敏感
Z-Score 标准化	将数据转换为均值为0，标准差为1的分布	理论上无界 (如 [-3, 3] 常见)	结果符合标准正态分布，对异常值相对稳健
非线性归一化	通过数学函数改变数据分布形状	取决于所用函数 (如 [0,1])	适用于处理数据分化较大（极端值多）的场景

🔢 详解不同归一化方法

下面我们具体看看这些方法是如何工作的：

1. Min-Max 归一化（线性）
   这是最常被理解为“转换到0-1区间”的方法。它的计算公式是：
   

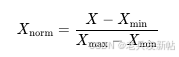
   这种方法确实将数据压缩到 [0, 1] 区间。它的优点是保留了原始数据之间的关系。但缺点也很明显：对异常值非常敏感。如果数据中有一个极大的值，会导致其他正常数据被压缩在一个很窄的范围内 。这种方法比较适用于数据范围边界比较清晰的情况，比如图像像素值（0-255）可以直接除以255归一化到[0,1] 。

2. Z-Score 标准化
   这种方法的目标是使数据符合均值为0、标准差为1的标准正态分布。它的计算公式是：
   

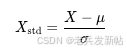
   其中，μ 是数据的均值，σ 是标准差。经过处理的数据没有绝对的边界，大部分数据会落在区间 [-3, 3] 内（根据正态分布的性质，约99.7%的数据落在此区间）。因为它依赖于数据的整体分布（均值和标准差），所以对异常值的敏感度低于Min-Max法 。当数据分布没有明显边界或存在极端值时，这种方法通常更合适。

3. 非线性归一化
   当数据分布极不均衡时，可能会使用对数、反正切等非线性函数进行转换 。例如：

   • 对数函数：X' = log(X)，常用于压缩数据规模。
   • 反正切函数：X' = arctan(X) * (2/π)，可以将数据映射到[-1, 1]区间。
     这些方法通过函数曲线形状的改变，对数据不同区间的缩放比例进行调整，而不是简单的线性变换。

💡 如何选择归一化方法

选择哪种方法，主要取决于你的数据特点和后续要使用的模型：

• 数据分布与边界：如果数据分布有清晰边界且不易受极端值影响，可考虑 Min-Max 归一化；如果数据分布没有明显边界或可能存在异常值，Z-Score 标准化通常是更稳妥的选择 。
• 模型需求：
  • 一些模型如支持向量机（SVM）、K-近邻（KNN）或基于梯度下降的算法（如神经网络），通常需要归一化来加快收敛速度并提升性能 。
  • 而像决策树、随机森林这类基于树结构的模型，对特征的量纲不敏感，通常不需要归一化 。
• 后续流程一致性：务必使用训练集计算得到的归一化参数（如Min、Max、μ、σ）来对测试集进行转换，避免数据泄露 。

希望这些解释能帮助你更全面地理解归一化。如果你对某个特定方法的应用场景有更具体的疑问，我们可以继续探讨。