当前位置：首页 > news >正文

密码学系列 - 零知识证明(ZKP) - NTT运算

news 2025/10/6 8:45:27

NTT（Number Theoretic Transform，数论变换）是一种与快速傅里叶变换（FFT）类似的技术，主要用于多项式的快速乘法计算，是实现同态加密、零知识证明等密码学应用的基础工具之一。

https://medium.com/@zkrush/a-behind-the-scenes-look-at-posw-on-aleo-6d7c2a939a3b

理解FFT的蝶形运算

数论变换（Number Theoretic Transform，NTT）通常用于加速多项式乘法, 但不包含椭圆曲线标量乘法运算。多项式乘法的卷积运算在时域中计算较慢，而通过 NTT，可以将多项式从时域转换到频域，在频域中可以简单地逐系数相乘来完成卷积操作，然后再通过逆 NTT 转回时域。这样可以显著提升多项式乘法的效率，从 $O(n^2)$ 降到 $\log n)$ 。

零知识证明Groth16的计算中为了计算H，采用了FFT计算。FFT的蝶形运算是理解FFT计算的基础。二分情况下的计算，相对清晰，算法导论给出了详细的推导过程。
对于熟悉主流零知识证明协议的人来说，你会知道两种类型的计算——NTT 和 MSM，是这些协议的核心。几乎所有主流的零知识证明协议都大量使用这两种计算（Marlin 使用 30+ 轮）。
Aleo 将 PoSW 设计为 NTT + MSM 计算。这实际上是从 Marlin 中提取了一些核心计算，与完整的 Marlin 证明相比，这是一个较小的单位。

Butterfly

Butterfly 算法通过分治、指数因子重用和位反转排列等方法，极大地减少了冗余运算，使 FFT 和 NTT 等大规模计算能够在== $\log n)$ 的复杂度==下完成。

假设要进行的是一个 n 点的 FFT 计算，Butterfly 算法的计算步骤如下：

输入排列（Bit-Reversal Permutation）：
- 对输入数据进行重新排列，使其符合分治算法的顺序。通常采用位反转（Bit-Reversal）方式排列，使数据的下标顺序与二进制位的反向排列对应。这一步是为了简化后续的分层计算过程。
分层计算：
- 将计算过程分成若干层，每一层都可以看作是一组小规模的 DFT(离散傅里叶变换)/IDFT 操作。在每一层中，子问题的规模逐渐增大，直到最后一层完成所有计算。
- 每一层的计算由多个“蝴蝶形”运算组成，每个蝴蝶运算只涉及两个数据点的计算。
蝴蝶形运算（Butterfly Computation）：
- 在每层中，将成对的数据点进行计算，每对点的运算过程如下：
  - 假设两个输入数据点为 x 和 y，则输出点为：
    
    $\cdot \omega$
    
    $\cdot \omega$
    
    其中，ω 是一个旋转因子，在 FFT 中是复数指数项，在 NTT 中是有限域上的根。
- 每一层的运算使用不同的旋转因子 $ω\omega$ ，从而逐步得到不同频率分量的结果。
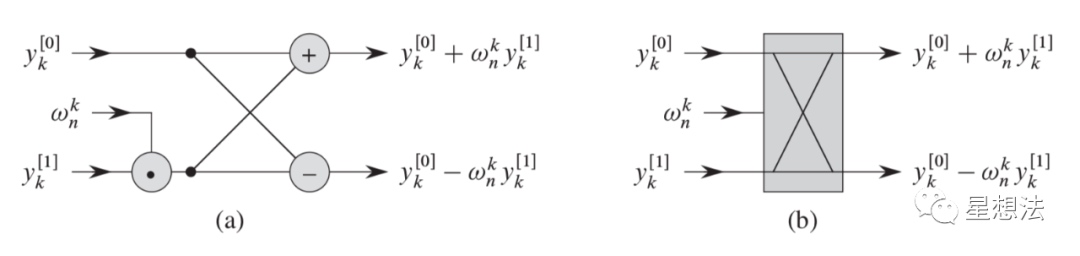
重复和合并：
- 通过重复上述分层和蝴蝶形运算，最终得到完整的频域表示。

NTT size

一套指令集需要 ntt size是 $2^{16}$ ~ $2^{19}$

/// Construct a domain that is large enough for evaluations of a polynomial
/// having `num_coeffs` coefficients.
pub fn new(num_coeffs: usize) -> Option<Self> {println!("test fft size: {}", size);