数据结构入门 (六)：公平的艺术 —— 深入理解队列

引言：从“插队”到“排队”

在上一篇文章中，我们认识了栈——一种“后进先出”的数据结构。它对于实现“撤销”等场景非常有效，但放在现实生活中，这可不太“公平”。

现在，让我们回归到生活中最常见的场景：排队。这里遵循着一个天经地义的规则——“先来后到”。

为了体现这个“公平”的规则，这次我们给线性表加上另一个约束：只允许在一端插入，而在另一端进行删除。这种“一头进，一头出”的受限线性表，就是我们今天的主角——队列。

我们把允许插入的一端标识为队尾，允许删除的一端标识为队头。在队尾插入元素叫做入队列，在队头删除元素叫做出队列。引入front和rear两个指针，front指向队头元素，rear指向队尾元素的下一个元素，当front == rear时，队列是空队列。

图1 队列：先进先出 (FIFO)

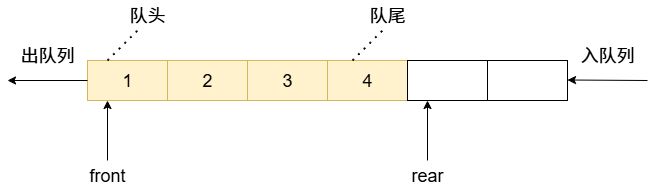
队列的核心特性是先进先出 (First-In, First-Out, FIFO)。这个特性使它成为任务调度、消息缓冲、广度优先搜索（BFS）算法等众多场景的基石。

一、顺序队列的“陷阱”与“进化”

1.朴素的实现与性能的烦恼

最直观的想法，就是用一个数组来实现队列，并且让数组下标0永远是队头。

• 入队：只需在数组末尾添加元素，rear指针后移，时间复杂度为O(1)。
• 出队：删除下标为0的元素后，如果要保证队列的队头在下标为0的位置，那么需要将后面所有元素向前移动，时间复杂度为O(n)。

这种每次出队都要动摇到所有元素的方式，在频繁出队的场景下，性能开销是巨大的。

2.解决办法与“假溢出”陷阱

为了让出队列也达到O(1)，我们可以在出队列时只移动front指针即可，无需搬移元素。

图2 “假溢出”现象

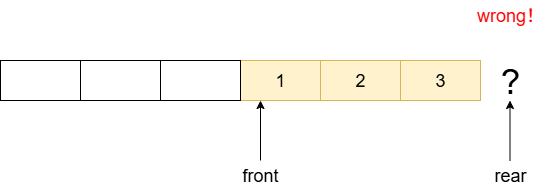
虽然这样子使得性能大大提高，但同时也面临着一个问题：随着不断的入队列和出队列，front和rear指针都会向后移动。当rear到达数组末尾时，我们便无法再入队列，即使在数组的前端因为出队列已经空了出来。我们把这种“数组明明有空位，却无法再插入”的现象叫“假溢出”。

3. 终极进化：循环队列

如何解决“假溢出”？答案是把笔直的数组“掰弯”，变成一个环——循环队列。当指针走到数组的尽头，我们通过取模运算让它“传送”回数组的开头。

图3 循环队列

这样，空间就得到了完美的复用。但新的挑战又来了：当队尾指针追上队头指针时（rear == front），我们无法判断队列是“空”还是“满”。

第一个解决方法是标识法。多设置一个变量flag，只要有插入就把flag设为1。如此，当rear == front且flag = 1时，队列为满；当rear == front且flag = 0时，队列为空。但这种方法效率相对较低。

第二个方法是牺牲一个存储单元。我们要留一个元素空间，试探如果rear指针往后走，是否会与front指针重合。也就是说队列满时，数组中还有一个空的元素，我们就把它看做队列已满。这个方法下队列空的判定条件还是rear == front，而队列满的判定条件是(rear + 1) % n == front。

二、循环队列的C语言实现

1.定义结构体与接口

#include <stdio.h>
#include <stdlib.h>#define MaxQueueSize 5
typedef int Element;typedef struct
{Element data[MaxQueueSize];int front; // 指向队头元素的下标int rear; // 指向队尾元素的下一个位置的下标
} ArrayQueue;void initArrayQueue(ArrayQueue *queue);int enArrayQueue(ArrayQueue *queue, Element e);
int desArrayQueue(ArrayQueue *queue, Element *e);

2.初始化队列

void initArrayQueue(ArrayQueue *queue)
{// 初始时，队头和队尾指针都指向0queue->front = queue->rear = 0;
}

3.入队列

int enArrayQueue(ArrayQueue *queue, Element e)
{// 1. 判断队列是否已满if ((queue->rear + 1) % MaxQueueSize == queue->front) {fprintf(stderr, "Queue is full\n");return -1;}// 2. 在 rear 指向的位置放入元素queue->rear = (queue->rear + 1) % MaxQueueSize;// 3. rear 指针后移 (取模确保循环)queue->data[queue->rear] = e;return 0;
}

4.出队列

int desArrayQueue(ArrayQueue *queue, Element *e)
{// 1. 判断队列是否为空if (queue->rear == queue->front){fprintf(stderr, "Queue is empty\n");return -1;}// 2. 从 front 指向的位置取出元素queue->front = (queue->front + 1) % MaxQueueSize;// 3. front 指针后移 (取模确保循环)*e = queue->data[queue->front];return 0;
}

5.测试函数

#include <stdio.h>
#include "arrayQueue.h"void test01()
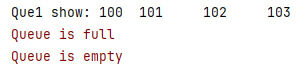
{ArrayQueue stu1;initArrayQueue(&stu1);for (int i = 0; i < 4; i++){enArrayQueue(&stu1, i + 100);}enArrayQueue(&stu1, 500);printf("DeQueue: ");Element x1;while (desArrayQueue(&stu1, &x1) != -1){printf("%d\t", x1);}printf("\n");
}int main()
{test01();return 0;
}

结果为：

三、链队列：无限延伸的队伍

循环队列虽好，但它依然有固定容量的限制。如果队列长度无法预估，链式队列则是更好的选择。它就像一条可以无限延伸的队伍，只要内存足够，就不会“溢出”。

队列的链式存储结构，其实就是只能尾进头出的单链表。为了操作方便，我们将队头指针指向链队列的头节点，而队尾指针指向最后一个节点。

图4 带头结点的链队列

四、链队列的C语言实现

1. 定义结构体与接口

typedef int Element;// 链表的节点
typedef struct _node
{Element data;struct _node *next;
} QueNode;// 链式队列的头节点
typedef struct
{QueNode *front; // 指向队列第一个节点QueNode *rear; // 指向队列最后一个节点int cnt; // 当前队列中元素个数const char *name; // 队列名称，可用于调试输出
} LinkQueue;LinkQueue *createLinkQueue(const char *name);
void releaseLinkQueue(LinkQueue *queue);int enLinkQueue(LinkQueue *queue, Element e);
int deLinkQueue(LinkQueue *queue, Element *e);

2.创建链队列

LinkQueue* createLinkQueue(const char *name)
{LinkQueue *queue = malloc(sizeof(LinkQueue));if(queue == NULL){fprintf(stderr, "createLinkQueue malloc failed!\n");return NULL;}queue->name = name;queue->front = queue->rear = NULL;queue->cnt = 0;return queue;
}

3.入队列

// 先有新节点，新节点应该向rear的next方向插入，便于front的删除
int enLinkQueue(LinkQueue* queue, Element e)
{QueNode *node = malloc(sizeof(QueNode));if (node == NULL){fprintf(stderr, "enLinkQueue new_node malloc failed!\n");return -1;}node->data = e; // 填充新节点数据node->next = NULL; // 新节点成为新的队尾if (queue->rear){// 队列非空：将新节点链接到队尾，并更新 rear 指针queue->rear->next = node;queue->rear = node;} else{// 队列为空：第一个节点既是front也是rear queue->rear = queue->front = node;}queue->cnt++;return 0;
}

4.出队列

int deLinkQueue(LinkQueue* queue, Element* e)
{if (queue->front == NULL){fprintf(stderr, "queue empty!\n");return -1;}// 取出队头节点的数据*e = queue->front->data;QueNode *tmp = queue->front;queue->front = tmp->next;free(tmp);queue->cnt--;// 特殊情况：如果出队后队列为空，需将 rear 也置为 NULLif (queue->front == NULL){queue->rear = NULL;}return 0;
}

5.释放链队列

void releaseLinkQueue(LinkQueue* queue)
{if(queue){QueNode *node;// 遍历并释放所有数据节点while(queue->front){node = queue->front;queue->front = node->next;free(node);queue->cnt--;}printf("queue have %d node!\n", queue->cnt);free(queue);}
}

五、总结：排队的智慧

队列，作为一种基础且重要的数据结构，其两种实现方式各有千秋：

特性	循环队列 (顺序)	链队列
空间使用	内存连续，缓存友好，但有“假溢出”风险和固定容量。	按需分配，无空间浪费，但有指针额外开销。
性能	入队出队均为O(1)，通常因缓存效应而更快。	入队出队均为O(1)，但malloc/free开销较大。
适用场景	容量可预估、对性能要求高的系统级编程（如OS任务调度、网络缓冲区）。	容量无法预估、业务逻辑实现（如订单处理系统）。

至此，我们已经掌握了两种最重要的“受限”线性结构：代表“后进先出”的栈，和代表“先进先出”的队列。它们是构建更复杂算法和系统的基本构件。

我们的线性结构探索之旅暂告一段落。在下一篇，我们将探讨一种更加高级的结构——树。