当前位置：首页 > news >正文

张量分解 | CP / Tucker / BTD

news 2025/10/6 7:44:16

注：本文为 “张量分解” 相关合辑。
图片清晰度受引文原图所限。
略作重排，如有内容异常，请看原文。

张量分解

张量介绍

张量（tensor）是一种多维数据存储形式，数据的维度被称为张量的阶。它可以视为向量和矩阵在多维空间中的推广，向量可看作一维张量，矩阵可看作二维张量。以下是一个三阶张量的例子，它有三个维度，即 3 个 mode：

三阶张量。

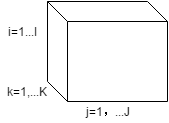需要注意的是，此处所说的张量是具有某种排列形式的数据集合，与物理中的张量场不同。

传统的处理高维数据的方法（如 ICA、PCA、SVD 和 NMF）通常将数据展成二维的矩阵形式进行处理，这种方式会使数据的结构信息丢失（例如图像的邻域信息丢失），导致求解过程往往变得病态。而采用张量对数据进行存储，能够保留数据的结构信息，因此在图像处理以及计算机视觉等领域得到了广泛应用。张量分解中常见的两种分解是 CP 分解（Canonical Polyadic Decomposition，CPD）和 Tucker 分解（Tucker Decomposition）。下面将重点介绍这两种分解，并阐述它们在图像处理中的一些应用。

张量定义及运算

张量（Tensor）

一个 $N$ 阶 $I1×I2×⋯×INI_{1} \times I_{2} \times \dots \times I_{N}$ 维的张量可以表示为 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 。张量中的每一个元素可以由 $yi1i2…iny_{i_{1} i_{2} \dots i_{n}}$ 表示，其中 $in∈{1,2,…,In}i_{n} \in \{1,2,\dots,I_{n}\}$ 。

纤维（Fiber）

纤维是指从张量中抽取向量的操作。类似于矩阵操作，固定其他维度，只保留一个维度变化，可以得到纤维的概念。例如，对上图中的三阶张量分别按照 I、J、K 三个 mode 进行 Fiber 操作，可以得到如图所示的 $x_{:jk}$ 、 $x_{i:k}$ 、 $x_{ij:}$ 三个维度的纤维：

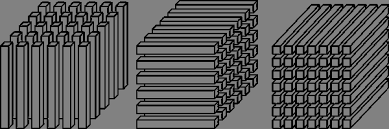三阶张量的 Fiber 。

切片（Slice）

切片操作是指在张量中抽取矩阵的操作。在张量中，若保留两个维度变化，其他维度固定，可以得到一个矩阵，该矩阵即为张量的切片。对图中的张量分别按照 I、J、K 三个方向进行操作，可以得到如图所示的 $x_{i::}$ 、 $x_{:j:}$ 、 $x_{::k}$ 三个维度的切片：

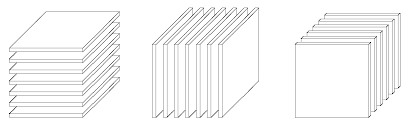三阶张量的 Slice 。

内积（Inner product）

两个大小相同的张量 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 的内积定义为张量中相对应的元素的乘积之和，即：
$⟨X,Y⟩=∑i1=1I1∑i2=1I2⋯∑iN=1INxi1i2…iNyi1i2…iN\langle X,Y \rangle = \sum_{i_{1}=1}^{I_{1}} \sum_{i_{2}=1}^{I_{2}} \dots \sum_{i_{N}=1}^{I_{N}} x_{i_{1} i_{2} \dots i_{N}} y_{i_{1} i_{2} \dots i_{N}}$
相应地，张量 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 的范数定义为：
$∥X∥=∑i1=1I1∑i2=1I2⋯∑iN=1INxi1i2…iN2\|X\| = \sqrt{\sum_{i_{1}=1}^{I_{1}} \sum_{i_{2}=1}^{I_{2}} \dots \sum_{i_{N}=1}^{I_{N}} x_{i_{1} i_{2} \dots i_{N}}^{2}}$
即所有元素的平方和的平方根。

矩阵展开（Unfolding-Matricization）

张量的矩阵展开是将一个张量的元素重新排列（即对张量的 mode-n 的纤维进行重新排列），得到一个矩阵的过程。张量 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 在第 $n$ 维度上展开矩阵表示为 $X(n)∈RIn×(I1×I2×…In−1In+1⋯×IN)X_{(n)} \in \mathbb{R}^{I_{n} \times (I_{1} \times I_{2} \times \dots I_{n-1} I_{n+1} \dots \times I_{N})}$ 。对一个三阶张量按照 I、J、K 三个方向进行矩阵展开得到的矩阵如下图：

三阶张量的矩阵展开。

外积（Outer Product）

定义张量 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 和张量 $\in \mathbb{R}^{J_{1} \times J_{2} \times \dots \times J_{M}}$ 的外积为：
$\circ Y \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N} \times J_{1} \times J_{2} \times \dots \times J_{M}}$
其中：
$zi1,i2,…,iN,j1,j2,…,jM=xi1,i2,…,iN×yj1,j2,…,jMz_{i_{1},i_{2},\dots,i_{N},j_{1},j_{2},\dots,j_{M}} = x_{i_{1},i_{2},\dots,i_{N}} \times y_{j_{1},j_{2},\dots,j_{M}}$
即张量 $Z$ 是张量 $X$ 和张量 $Y$ 中的每一个元素的乘积构成的。特别地，如果 $X$ 和 $Y$ 分别是一个向量，那么它们的外积是一个秩为 1 的矩阵；如果 $X$ 、 $Y$ 和 $Z$ 分别是一个向量，那么它们的外积是一个秩为 1 的三阶张量。

Kronecker 乘积（Kronecker Product）

Kronecker 乘积定义在两个矩阵 $A∈RI×J\mathbf{A} \in \mathbb{R}^{I \times J}$ 、 $B∈RK×L\mathbf{B} \in \mathbb{R}^{K \times L}$ 上的运算：

$A⊗B=[a11Ba12B⋯a1JBa21Ba22B⋯a2JB⋮⋮⋱⋮aI1BaI2B⋯aIJB]∈RIK×JL\mathbf{A} \otimes \mathbf{B} = \begin{bmatrix} a_{11}\mathbf{B} & a_{12}\mathbf{B} & \cdots & a_{1J}\mathbf{B} \\ a_{21}\mathbf{B} & a_{22}\mathbf{B} & \cdots & a_{2J}\mathbf{B} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}\mathbf{B} & a_{I2}\mathbf{B} & \cdots & a_{IJ}\mathbf{B} \end{bmatrix} \in \mathbb{R}^{IK \times JL}$

Hadamard 乘积（Hadamard Product）

Hadamard 乘积定义在两个相同大小的矩阵 $A∈RI×J\mathbf{A} \in \mathbb{R}^{I \times J}$ 、 $B∈RI×J\mathbf{B} \in \mathbb{R}^{I \times J}$ 上的运算：

$A∗B=[a11b11a12b12⋯a1Jb1Ja21b21a22b22⋯a2Jb2J⋮⋮⋱⋮aI1bI1aI2bI2⋯aIJbIJ]∈RI×J\mathbf{A} * \mathbf{B} = \begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} & \cdots & a_{1J}b_{1J} \\ a_{21}b_{21} & a_{22}b_{22} & \cdots & a_{2J}b_{2J} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}b_{I1} & a_{I2}b_{I2} & \cdots & a_{IJ}b_{IJ} \end{bmatrix} \in \mathbb{R}^{I \times J}$

Khatri-Rao 乘积（Khatri-Rao Product）

Khatri-Rao 乘积定义了两个相同列数的矩阵 $A∈RI×K\mathbf{A} \in \mathbb{R}^{I \times K}$ 、 $B∈RJ×K\mathbf{B} \in \mathbb{R}^{J \times K}$ 上的操作，其过程如下图所示：
$A⊙B=[a1⊗b1a2⊗b2…aK⊗bK]∈RIJ×K\mathbf{A} \odot \mathbf{B} = \left[ \begin{array}{cccc} \mathbf{a}_{1} \otimes \mathbf{b}_{1} & \mathbf{a}_{2} \otimes \mathbf{b}_{2} & \dots & \mathbf{a}_{K} \otimes \mathbf{b}_{K} \end{array} \right] \in \mathbb{R}^{IJ \times K}$
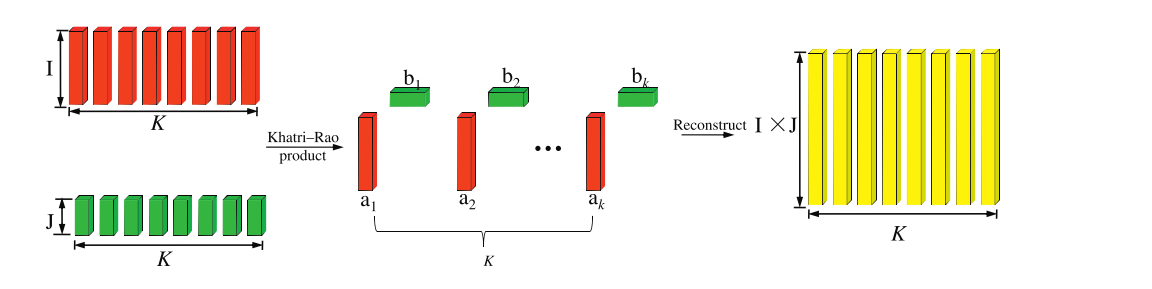三阶张量的 Khatri-Rao 乘积。

张量与矩阵的模积（Mode-n Product）

张量与矩阵的模积定义了一个张量 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 和一个矩阵 $U∈RJ×In\mathbf{U} \in \mathbb{R}^{J \times I_{n}}$ 的 n-mode 乘积 $\times_{n} \mathbf{U}) \in \mathbb{R}^{I_{1} \times \dots \times I_{n-1} \times J \times I_{n+1} \times \dots \times I_{N}}$ ，其元素定义为：
$\times_{n} \mathbf{U})_{i_{1} \dots i_{n-1} j i_{n+1} \dots i_{N}} = \sum_{i_{n}=1}^{I_{n}} x_{i_{1} i_{2} \dots i_{N}} u_{j i_{n}}$
该定义可以写成沿 mode-n 展开的形式为：
$\times_{n} \mathbf{U} \Leftrightarrow \mathbf{Y}_{(n)} = \mathbf{U} \mathbf{X}_{(n)}$
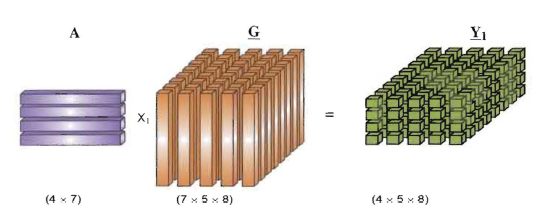
如果 $J < I_{n}$ ，那么张量和矩阵的乘积可以看作是一个降维的过程，它把一个高维度的张量映射到一个低维度的张量空间。图 \ref{fig:tensorMatrixProduct} 演示了一个张量 $\in \mathbb{R}^{7 \times 5 \times 8}$ 和一个矩阵 $\in \mathbb{R}^{4 \times 7}$ 的乘积最终得到张量 $\in \mathbb{R}^{4 \times 5 \times 8}$ ，张量的第一个维度由 7 变成了 4。

张量与矩阵的模积。

张量与向量的模积（Mode-n Product）

张量与向量的模积定义了一个张量 $\in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 与向量 $v∈RIn\mathbf{v} \in \mathbb{R}^{I_{n}}$ 的运算为：
$\times_{n} \mathbf{v})_{i_{1} \dots i_{n-1} i_{n+1} \dots i_{N}} = \sum_{i_{n}=1}^{I_{n}} x_{i_{1} i_{2} \dots i_{N}} v_{i_{n}}$
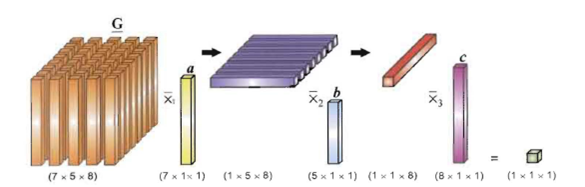
一个向量和一个张量进行模乘可以减少张量的阶数，下图演示了一个张量的阶数由 3 阶变为 0 阶的过程。

在这里插入图片描述

张量分解 - CP 分解

CP 分解（Canonical Polyadic Decomposition）

1927 年，Hitchcock 提出了 CP 分解。CP 分解将一个 $N$ 阶张量 $X∈RI1×I2×⋯×IN\mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ 分解为 $R$ 个秩为 1 的张量和的形式，即：
$X=∑r=1Rλrar(1)∘ar(2)∘⋯∘ar(N)\mathcal{X} = \sum_{r=1}^{R} \lambda_{r} a_{r}^{(1)} \circ a_{r}^{(2)} \circ \dots \circ a_{r}^{(N)}$
通常情况下， $a_{r}^{(n)}$ 是一个单位向量。定义 $A(n)=[a1na2n…aRn]A^{(n)} = [a_{1}^{n} \ a_{2}^{n} \ \dots \ a_{R}^{n}]$ ， $\text{diag}(\lambda)$ ，那么上述公式可以写为：
$X=D×1A(1)×2A(2)⋯×NA(N)\mathcal{X} = D \times_{1} A^{(1)} \times_{2} A^{(2)} \cdots \times_{N} A^{(N)}$
矩阵的表达形式为：
$X(n)=AnD(A(N)⨀⋯⨀A(n+1)⨀A(n−1)⋯⨀A1)TX_{(n)} = A^{n} D (A^{(N)} \bigodot \dots \bigodot A^{(n+1)} \bigodot A^{(n-1)} \dots \bigodot A^{1})^{T}$
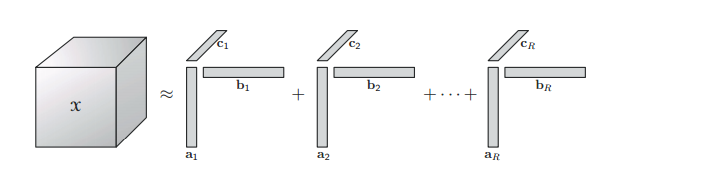
当张量 $X\mathcal{X}$ 的阶数为 3 时，其分解的形式如下图所示：

三阶张量的 CP 分解。

张量的低秩近似

在矩阵中，定义最小的秩为 1 的矩阵和的个数为矩阵的秩。类似地， $R$ 的最小值为张量的秩，记作 $Rank(X)=R\text{Rank}(\mathcal{X}) = R$ ，这样的 CP 分解也称为张量的秩分解。需要注意的是，在张量中，秩的定义是不唯一的，张量秩的个数求解是一个 NP 问题。对于一个矩阵 $A$ ，其 SVD 分解定义为：
$\sum_{r=1}^{R} \sigma_{r} u_{r} \circ v_{r}, \quad \sigma_{1} \geq \sigma_{2} \geq \dots \geq \sigma_{R} \geq 0$
取 SVD 分解得到的前 $k$ 个因子作为矩阵 $A$ 的近似，可以得到矩阵 $A$ 的低秩近似。类似地，取张量的前 $k$ 个因子作为张量 $X\mathcal{X}$ 的低秩近似，即：
$X=∑k=1Kλkak(1)∘ak(2)∘⋯∘ak(N)\mathcal{X} = \sum_{k=1}^{K} \lambda_{k} a_{k}^{(1)} \circ a_{k}^{(2)} \circ \dots \circ a_{k}^{(N)}$
与矩阵的低秩近似不同，张量的最佳 Rank-n 近似并不包括在其最佳 Rank-(n+1) 近似中，即张量的秩 Rank-n 近似无法渐进地得到。

CP 的求解

CP 分解的求解首先要确定分解的秩 1 张量的个数。由于张量的秩 Rank-n 近似无法渐进地得到，通常通过迭代的方法对 $R$ 从 1 开始遍历，直到找到一个合适的解。当数据无噪声时，重构误差为 0 所对应的解即为 CP 分解的解；当数据有噪声时，可以通过 CORCONDIA 算法估计 $R$ 。当分解的秩 1 张量的个数确定下来之后，可以通过交替最小二乘方法对 CP 分解进行求解。以下以三阶张量为例对 ALS 算法进行阐述。

假设 $X∈RI×J×K\mathcal{X} \in \mathbb{R}^{I \times J \times K}$ 是一个三阶张量，对它进行张量分解的目标表达式为：
$min⁡X^∥X−X^∥,X^=∑r=1Rλrar∘br∘cr=[[λ;A,B,C]]\min_{\hat{\mathcal{X}}} \| \mathcal{X} - \hat{\mathcal{X}} \|, \quad \hat{\mathcal{X}} = \sum_{r=1}^{R} \lambda_{r} a_{r} \circ b_{r} \circ c_{r} = \left[\kern-0.15em\left[ \lambda ; A,B,C \right]\kern-0.15em\right]$
ALS 算法首先固定 $B$ 、 $C$ 去求解 $A$ ，接着固定 $A$ 和 $C$ 去求解 $B$ ，然后固定 $B$ 和 $C$ 去求解 $A$ ，如此不断重复迭代直到达到收敛条件。固定矩阵 $B$ 和 $C$ ，可以得到上述式子在 mode-1 矩阵展开时的形式为：
$min⁡A^∥X(1)−A^(C⊙B)T∥F\min_{\hat{A}} \| X_{(1)} - \hat{A} (C \odot B)^{T} \|_{F}$
其中 $A^=A⋅diag(λ)\hat{A} = A \cdot \text{diag}(\lambda)$ ，那么上述式子的最优解为：
$A^=X(1)[(C⊙B)T]†\hat{A} = X_{(1)} [(C \odot B)^{T}]^{\dagger}$
为了防止数值计算的病态问题，通常将 $A^\hat{A}$ 的每一列单位化，即 $λr=∥a^r∥\lambda_{r} = \| \hat{a}_{r} \|$ ， $ar=a^r/λra_{r} = \hat{a}_{r} / \lambda_{r}$ 。将上述式子推广到高阶形式，可以得到：
$A(n)=Xn(A(N)⨀⋯⨀A(n+1)⨀A(n−1)⋯⨀A1)V†其中V=A(1)T(A(1)⨀⋯⨀A(n−1)⨀A(n+1)⋯⨀A(N)TA(N))\begin{aligned} & A^{(n)} = X^{n} (A^{(N)} \bigodot \dots \bigodot A^{(n+1)} \bigodot A^{(n-1)} \dots \bigodot A^{1}) V^{\dagger} \\ & \text{其中} \quad V = A^{(1)T} (A^{(1)} \bigodot \dots \bigodot A^{(n-1)} \bigodot A^{(n+1)} \dots \bigodot A^{(N)T} A^{(N)}) \end{aligned}$
对于一个 $N$ 阶张量 $X$ ，其 ALS 求解的步骤如下图所示。它假设分解出 Rank-1 张量的个数 $R$ 是事先已知的。对于各个因子的初始化，可以采用随机初始化，也可以通过以下式子进行初始化：
$n=1,…,NA^{(n)} = R \quad \text{leading left singular vectors of} \ X_{(n)} \ \text{for} \ n=1,\dots,N$
CP 分解算法。

可加约束

在一些应用中，为了使 CP 分解更加鲁棒和精确，可以在分解出的因子上加上一些先验知识，即约束。例如，平滑约束（smooth）、正交约束、非负约束（nonnegative）、稀疏约束（sparsity）等。

CP 分解应用

CP 分解已在信号处理、视频处理、语音处理、计算机视觉、机器学习等领域得到了广泛应用。以下以去噪为例，阐述 CP 分解在高光谱图像处理中的应用。

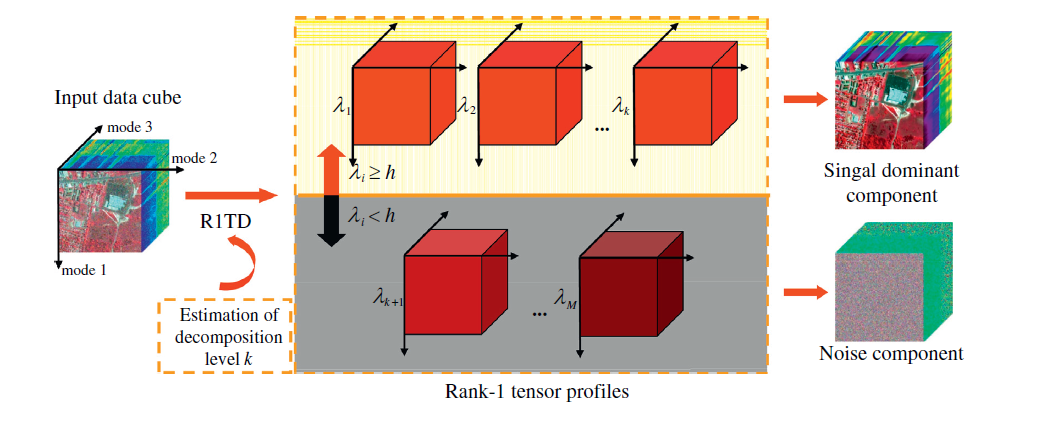
高光谱图像（HSI）是上个世纪 80 年代以来新兴的一种新型成像技术，它包括了可见光和不可见光范围的几十到几百个连续光谱窄波段，形成了一种数据立方体结构的图像。高光谱图像可以看作是一个三阶张量，图像的空间域和光谱域构成了数据的三个维度。采用低秩 CP 分解对高光谱图像去噪，认为低秩的部分是无噪声的部分，剩下的部分被认为是噪声数据，其示意图如下图所示：

CP 分解算法用于 HSI 去噪。

从图中可以看出，一个高光谱图像数据 $X\mathcal{X}$ 可以由两部分组成，即：
$X=S+N\mathcal{X} = \mathcal{S} + \mathcal{N}$
其中， $S\mathcal{S}$ 被认为是低秩的部分，即干净的图像； $N\mathcal{N}$ 是噪声的部分（这里的噪声包括白噪声、高斯噪声等）。可以通过对原始数据 $X\mathcal{X}$ 进行低秩 CP 分解来得到 $S\mathcal{S}$ 。在 Urban 数据上进行去噪，得到去噪前的数据和去噪之后的数据图分别如下图所示。从图中可以看出，采用 CP 分解可以对高光谱图像进行去噪。

有噪声图像处理之后的图像。

张量分解 - Tucker 分解

Tucker 分解

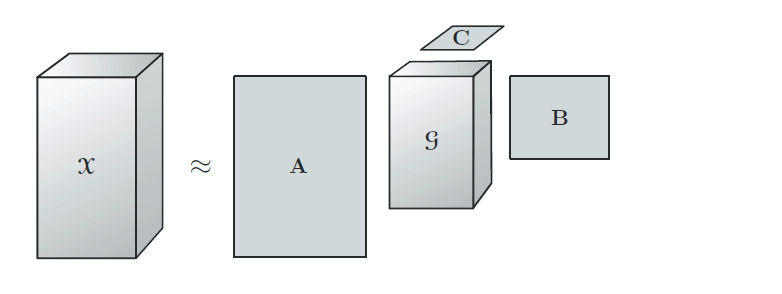
Tucker 分解最早由 Tucker 在 1966 年提出。一个三阶张量的 Tucker 分解的图示如下图所示：

三阶张量的 Tucker 分解。

对于一个三阶张量 $X∈RI×J×K\mathcal{X} \in \mathbb{R}^{I \times J \times K}$ ，Tucker 分解可以得到 $\in \mathbb{R}^{I \times P}$ 、 $\in \mathbb{R}^{J \times Q}$ 、 $\in \mathbb{R}^{K \times R}$ 三个因子矩阵和一个核张量 $G∈RP×Q×R\mathcal{G} \in \mathbb{R}^{P \times Q \times R}$ 。每个 mode 上的因子矩阵称为张量在每个 mode 上的基矩阵或主成分，因此 Tucker 分解又称为高阶 PCA、高阶 SVD 等。从图中可以看出，CP 分解是 Tucker 分解的一种特殊形式：如果核张量的各个维数相同并且是对角的，则 Tucker 分解就退化成了 CP 分解。

在三阶张量形式中，有：
$X=G×1A×2B×3C=∑p=1P∑q=1Q∑r=1Rgpqrap∘bq∘cr=[[G;A,B,C]]\mathcal{X} = \mathcal{G} \times_{1} A \times_{2} B \times_{3} C = \sum_{p=1}^{P} \sum_{q=1}^{Q} \sum_{r=1}^{R} g_{pqr} a_{p} \circ b_{q} \circ c_{r} = \left[\kern-0.15em\left[ \mathcal{G} ; A,B,C \right]\kern-0.15em\right]$
将上述公式写成矩阵的形式为：
$X1=AG(1)(C⊗B)TX2=BG(2)(C⊗A)TX3=CG(3)(B⊗A)T\begin{aligned} & X_{1} = A G_{(1)} (C \otimes B)^{T} \\ & X_{2} = B G_{(2)} (C \otimes A)^{T} \\ & X_{3} = C G_{(3)} (B \otimes A)^{T} \end{aligned}$
对于三阶张量，固定一个因子矩阵为单位阵，就得到 Tucker 分解的一个重要特例：Tucker2。例如，固定 $C = I$ ，则退化为：
$X=G×1A×2B=[[G;A,B,I]]\mathcal{X} = \mathcal{G} \times_{1} A \times_{2} B = \left[\kern-0.15em\left[ \mathcal{G} ; A,B,I \right]\kern-0.15em\right]$
进一步地，如果固定两个因子矩阵，就得到了 Tucker1。例如，固定 $C = I$ 、 $B = I$ ，则 Tucker 分解就退化成了普通的 PCA：
$X=G×1A=[[G;A,I,I]]\mathcal{X} = \mathcal{G} \times_{1} A = \left[\kern-0.15em\left[ \mathcal{G} ; A,I,I \right]\kern-0.15em\right]$
将上述公式推广到 $N$ 阶的模型，即可得到：
$X=G×1A(1)×2A(2)⋯×(N)A(N)=[[G;A(1),A(2),…,A(N)]]\mathcal{X} = \mathcal{G} \times_{1} A^{(1)} \times_{2} A^{(2)} \cdots \times_{(N)} A^{(N)} = \left[\kern-0.15em\left[ \mathcal{G} ; A^{(1)}, A^{(2)}, \dots, A^{(N)} \right]\kern-0.15em\right]$
写成矩阵形式为：
$X(n)=A(n)G(n)(A(N)⊗⋯⊗A(n+1)⊗A(n−1)⋯⊗A(1))TX_{(n)} = A^{(n)} G_{(n)} (A^{(N)} \otimes \dots \otimes A^{(n+1)} \otimes A^{(n-1)} \dots \otimes A^{(1)})^{T}$

$n$ -秩与低秩近似

$n$ -秩又称为多线性秩。一个 $N$ 阶张量 $X\mathcal{X}$ 的 $n$ -mode 秩定义为：
$rankn(X)=rank(X(n))\text{rank}_{n}(\mathcal{X}) = \text{rank}(X_{(n)})$
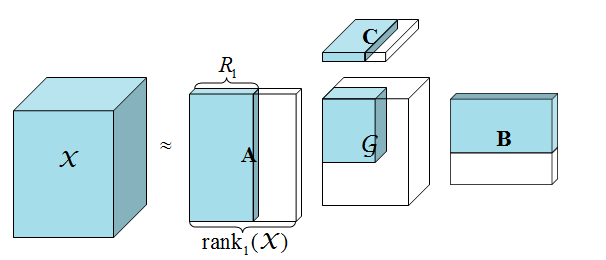
令 $rankn(X)=Rn\text{rank}_{n}(\mathcal{X}) = R_{n}$ ， $\dots, N$ ，则 $X\mathcal{X}$ 被称为秩 $(R1,R2,…,Rn)(R_{1}, R_{2}, \dots, R_{n})$ 的张量。 $R_{n}$ 可以看作是张量 $X\mathcal{X}$ 在各个 mode 上 fiber 所构成的空间的维度。如果 $rankn(X)=Rn\text{rank}_{n}(\mathcal{X}) = R_{n}$ ， $\dots, N$ ，则很容易得到 $X\mathcal{X}$ 的一个精确秩 $(R1,R2,…,RN)(R_{1}, R_{2}, \dots, R_{N})$ Tucker 分解；然而，如果至少有一个 $n$ 使得 $rankn(X)>Rn\text{rank}_{n}(\mathcal{X}) > R_{n}$ ，则通过 Tucker 分解得到的就是 $X\mathcal{X}$ 的一个秩 $(R1,R2,…,RN)(R_{1}, R_{2}, \dots, R_{N})$ 近似。下图展示了一个三阶张量的低秩近似，这在图像处理中可以认为是干净的图像：

三阶张量的低秩近似。

Tucker 分解的求解

对于固定的 $n$ -秩，Tucker 分解的唯一性不能保证，一般加上一些约束，如分解得到的因子单位正交约束等。例如，HOSVD（High Order SVD）求解算法通过张量的每一个 mode 上做 SVD 分解对各个 mode 上的因子矩阵进行求解，最后计算张量在各个 mode 上的投影之后的张量作为核张量。其算法过程如下图所示：

HOSVD 。

虽然利用 SVD 对每个 mode 做一次 Tucker1 分解，但 HOSVD 不能保证得到一个较好的近似。然而，HOSVD 的结果可以作为其他迭代算法（如 HOOI）的一个很好的初始化。HOOI（High-order Orthogonal Iteration）算法将张量分解看作是一个优化的过程，不断迭代得到分解结果。假设有一个 $N$ 阶张量 $X∈RI1×I2×⋯×IN\mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}$ ，那么对 $X\mathcal{X}$ 进行分解就是对以下问题进行求解：
$∣X−[[G;A(1),…,A(N)]]∣=∣vec(X)−(A(N)⊗⋯⊗A(1))vec(G)∣\begin{aligned} & \left| \mathcal{X} - \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right| \\ = & \left| \text{vec}(\mathcal{X}) - \left( \mathbf{A}^{(N)} \otimes \dots \otimes \mathbf{A}^{(1)} \right) \text{vec}(\mathcal{G}) \right| \end{aligned}$
将上述目标函数进一步化简得到：
$∥X−[[G;A(1),…,A(N)]]∥2=∥X∥2−2⟨X,[[G;A(1),…,A(N)]]⟩+∥[[G;A(1),…,A(N)]]∥2=∥X∥2−2⟨X×1A(1)T⋯×NA(N)T,G⟩+∥G∥2=∥X∥2−2⟨G,G⟩+∥G∥2\begin{aligned} & \left\| \mathcal{X} - \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right\|^{2} \\ = & \left\| \mathcal{X} \right\|^{2} - 2 \left\langle \mathcal{X}, \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right\rangle + \left\| \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right\|^{2} \\ = & \left\| \mathcal{X} \right\|^{2} - 2 \left\langle \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T}, \mathcal{G} \right\rangle + \left\| \mathcal{G} \right\|^{2} \\ = & \left\| \mathcal{X} \right\|^{2} - 2 \left\langle \mathcal{G}, \mathcal{G} \right\rangle + \left\| \mathcal{G} \right\|^{2} \end{aligned}$
而 $G\mathcal{G}$ 满足：
$G=X×1A(1)T⋯×NA(N)T\mathcal{G} = \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T}$
从而可以得到：
$∥X∥2−∥X×1A(1)T⋯×NA(N)T∥2\left\| \mathcal{X} \right\|^{2} - \left\| \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T} \right\|^{2}$
由于 $∥X∥\|\mathcal{X}\|$ 是一个常数，最小化上述式子相当于最大化：
$orthogonal\begin{aligned} & \max \left\| \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T} \right\| \\ \text{subject to} \quad & \mathbf{A}^{(n)} \in \mathbb{R}^{I_{n} \times R_{n}} \quad \text{and} \quad \text{columnwise orthogonal} \end{aligned}$
写成矩阵形式为：
$max⁡∥A(n)TW∥s.t.W=X(n)(A(N)⊗⋯⊗A(n+1)⊗A(n−1)⋯⊗A(1))\begin{aligned} & \max \left\| \mathbf{A}^{(n)T} \mathbf{W} \right\| \\ \text{s.t.} \quad & \mathbf{W} = \mathbf{X}_{(n)} \left( \mathbf{A}^{(N)} \otimes \dots \otimes \mathbf{A}^{(n+1)} \otimes \mathbf{A}^{(n-1)} \dots \otimes \mathbf{A}^{(1)} \right) \end{aligned}$
这个问题可以通过令 $A(n)\mathbf{A}^{(n)}$ 为 $W$ 的前 $R_{n}$ 个左奇异值向量来进行求解。HOOI 算法的过程如下图所示：

HOOI 算法。

约束 Tucker 分解

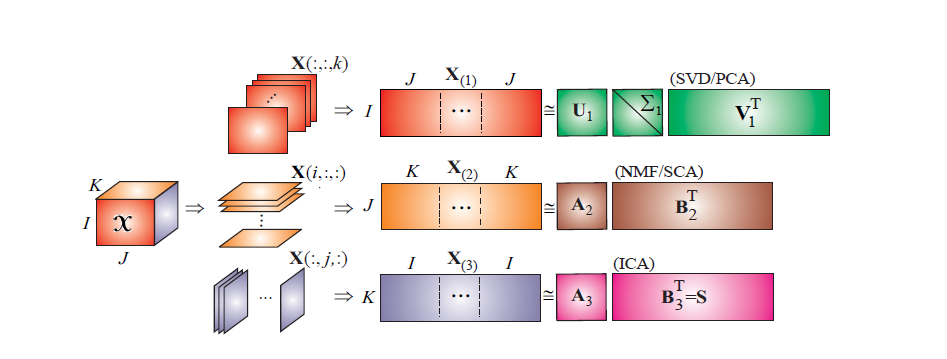
除了可以在 Tucker 分解的各个因子矩阵上加上正交约束以外，还可以加一些其他约束，比如稀疏约束、平滑约束、非负约束等。另外，在一些应用场景中，不同 mode 的物理意义不同，可以加上不同的约束。在下图中，在三个不同的 mode 上分别加上了正交约束、非负约束以及统计独立性约束等：

约束 Tucker 分解。

Tucker 分解的应用

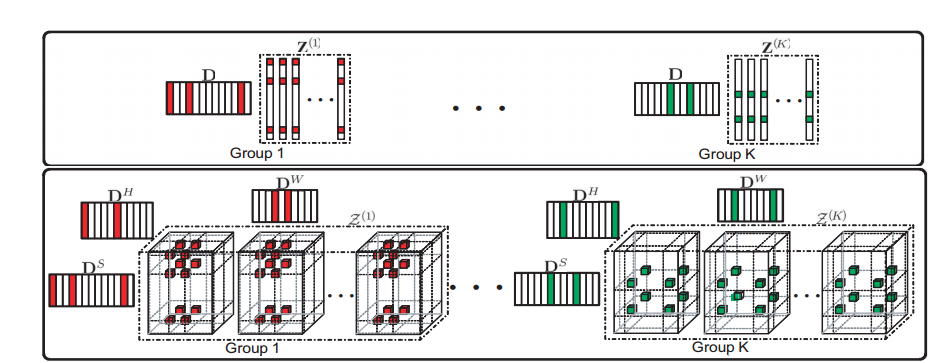
前面提到，Tucker 分解可以看作是 PCA 的多线性版本，因此可以用于数据降维、特征提取、张量子空间学习等。例如，一个低秩的张量近似可以用于去噪操作等。Tucker 分解同时在高光谱图像中也有所应用，如用低秩 Tucker 分解进行高光谱图像的去噪，用张量子空间进行高光谱图像的特征选择，用 Tucker 分解进行数据的压缩等。以下以高光谱图像去噪为例进行介绍。http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6909773 中对高光谱图像去噪的流程如下图所示：

高光谱图像去噪流程。

它首先对高光谱图像进行分块，然后对分块进行聚类，得到一些 group，最后对各个 group 里面的数据进行低秩 Tucker 分解。处理之前的噪声图像和处理之后的图像的对比如下图所示，可以发现 Tucker 分解可以对高光谱数据进行有效的去噪处理：

有噪声图像处理之后的图像。

张量分解 - Block Term Decomposition (BTD)

去年差不多这个时候，我在本人的博客上发表了三篇关于张量分解的博客，从百度统计来看，很多人阅读了这三篇博文。今天，我再介绍一种张量分解 - Block Term Decomposition (BTD)，以下将分几个部分对 BTD 进行介绍。

从 CP 分解到 BTD

在 CP 分解中，我们将一个张量分解为 $K$ 个 Rank-1 的成员张量的形式，写成公式即为：
$T=∑r=1Kar∘br∘cr=∑r=1K(arbrT)∘cr\mathcal{T} = \sum_{r=1}^{K} a_{r} \circ b_{r} \circ c_{r} = \sum_{r=1}^{K} (a_{r} b_{r}^{T}) \circ c_{r}$
显然， $a_{r} b_{r}^{T}$ 是一个 Rank-1 的矩阵，即一个低秩矩阵。而低秩往往是一些局部的特征，例如人的眉毛通常是低秩的。然而，在一些应用中，我们希望得到不同秩的特征，或者是不同尺度的特征，例如对于人脸，我们希望得到鼻子、眉毛、嘴巴、脸型等特征，此时 CP 分解就无法直观地做到。

基于 CP 分解，我们设想，如果 $a_{r} b_{r}^{T}$ 不是一个秩为 1 的矩阵，而是一个秩为 $L_{r}$ 的矩阵，那么显然 $a_{r}$ 和 $b_{r}$ 就不是一个向量，而是一个秩为 $L_{r}$ 的矩阵。于是得到了 BTD 模型的一种形式：
$T=∑r=1KArBrT∘cr\mathcal{T} = \sum_{r=1}^{K} A_{r} B_{r}^{T} \circ c_{r}$
可以将这个模型进一步推导，得到 BTD 的通俗形式。

BTD 分解概览

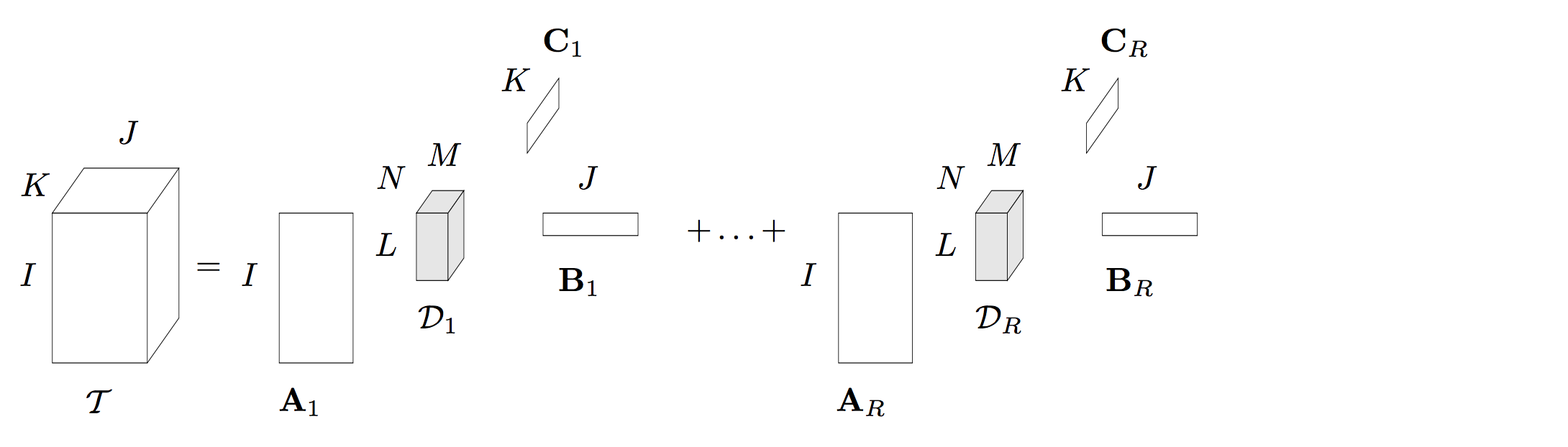
2008 年，Lieven De Lathauwer 等人提出了一种 Block Term Decomposition（BTD），这种张量分解在一些论文中也被称为 Block Component Decomposition (BCD)。本人认为叫 BCD 更合理一些，因为这种张量分解将一个 $N$ 阶张量分解为 $R$ 个成员张量的形式，BCD 更符合。如下图就是一个 $Rank−(Lr,Mr,Nr)\text{Rank}-(L_{r}, M_{r}, N_{r})$ 的分解，每一个成员张量是一个 $Rank−(Lr,Mr,Nr)\text{Rank}-(L_{r}, M_{r}, N_{r})$ 的 Tucker 分解：

Block Term Decomposition (BTD) 。

采用数学表达式可以写为：
$T=∑r=1RDr×1Ar×2Br×3Cr\mathcal{T} = \sum_{r=1}^{R} \mathcal{D}_{r} \times_{1} A_{r} \times_{2} B_{r} \times_{3} C_{r}$
其中 $Dr\mathcal{D}_{r}$ 是一个 $Rank−(Lr,Mr,Nr)\text{Rank}-(L_{r}, M_{r}, N_{r})$ 的张量， $Ar∈RI×LA_{r} \in \mathbb{R}^{I \times L}$ 是一个秩为 $I$ 的矩阵。显然，BTD 分解可以看作是之前介绍的 Tucker 分解和 CP 分解的结合形式。当 $R = 1$ 时，显然成员张量只有一个，此时这个分解就是一个 $Rank−(L,M,N)\text{Rank}-(L, M, N)$ 的 Tucker 分解。而当每一个成员张量是一个 $Rank−1\text{Rank}-1$ 分解时，该分解退化为一个 CP 分解（CP 分解是将一个张量分解为 $R$ 个秩为 1 的张量分解形式）。这也说明了，BTD 分解具有很强的泛化能力。论文 http://epubs.siam.org/doi/pdf/10.1137/070690730 同时对它的唯一性进行了证明，从证明来看，该算法的唯一性的条件要比 Tucker 分解和 CP 分解的唯一性要弱。

BTD 分解的求解

BTD 分解的求解算法有很多种，例如非线性最小二乘法 http://epubs.siam.org/doi/abs/10.1137/110832124，交替最小二乘算法（ALS），张量对角算法等。其中，交替最小二乘算法形式最为简单。以下以一个三阶张量 $T∈RI×J×K\mathcal{T} \in \mathbb{R}^{I \times J \times K}$ 为例，介绍这种求解算法。

定义 $[A_{1}, \dots, A_{R}]$ ， $[B_{1}, \dots, B_{R}]$ ， $[C_{1}, \dots, C_{R}]$ ，将 BTD 写为矩阵的形式，可以得到如下三个表达式：
$TJK×I=(B⊗C)⋅Blockdiag(D1MN×L,…,DRMN×L)ATTKI×J=(C⊗A)⋅Blockdiag(D1NL×M,…,DRNL×M)BTTIJ×K=(A⊗B)⋅Blockdiag(D1LM×N,…,DRLM×N)CT\begin{aligned} & T_{JK \times I} = (B \otimes C) \cdot \text{Blockdiag}(\mathcal{D}_{1_{MN \times L}}, \dots, \mathcal{D}_{R_{MN \times L}}) A^{T} \\ & T_{KI \times J} = (C \otimes A) \cdot \text{Blockdiag}(\mathcal{D}_{1_{NL \times M}}, \dots, \mathcal{D}_{R_{NL \times M}}) B^{T} \\ & T_{IJ \times K} = (A \otimes B) \cdot \text{Blockdiag}(\mathcal{D}_{1_{LM \times N}}, \dots, \mathcal{D}_{R_{LM \times N}}) C^{T} \end{aligned}$
当更新某一个因子矩阵或张量时，固定其他元素即可进行求解。例如，当求解 $A$ 时，固定 $Dr\mathcal{D}_{r}$ 和 $B$ 以及 $C$ ，设置 $\otimes C) \cdot \text{Blockdiag}(\mathcal{D}_{1_{MN \times L}}, \dots, \mathcal{D}_{R_{MN \times L}})$ ，因此可以得到 $A$ 的更新规则为：
$M^{\dagger} T_{JK \times I}$
同理可以得到其他矩阵或张量的更新规则。因此，采用 ALS 算法求解 BTD 的步骤如下图所示：

BTD 求解。

算法中的 QR 分解是为了防止算法出现数值计算错误。

特殊 BTD 分解

在前面已经介绍了 BTD 分解的两种特殊形式：Tucker 分解和 CP 分解。以下再介绍两种特殊的张量分解。

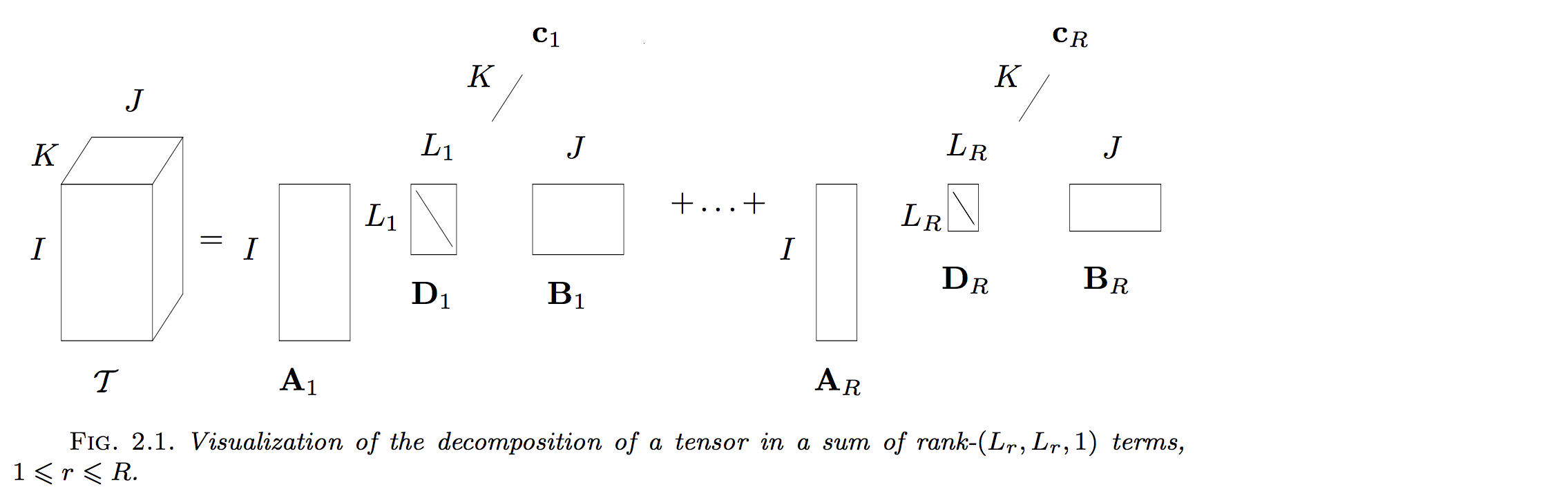
Rank- $L_{r}, L_{r}, 1)$ 分解

当每一个成员张量退化为 $Lr×LrL_{r} \times L_{r}$ 的矩阵时，可以得到 $Rank−(Lr,Lr,1)\text{Rank}-(L_{r}, L_{r}, 1)$ 分解，即：

$Rank-(L_{r}, L_{r}, 1) 分解$ 。

相应的求解算法与 BTD 算法类似，只是没有最后一步求解 core tensor 的部分：

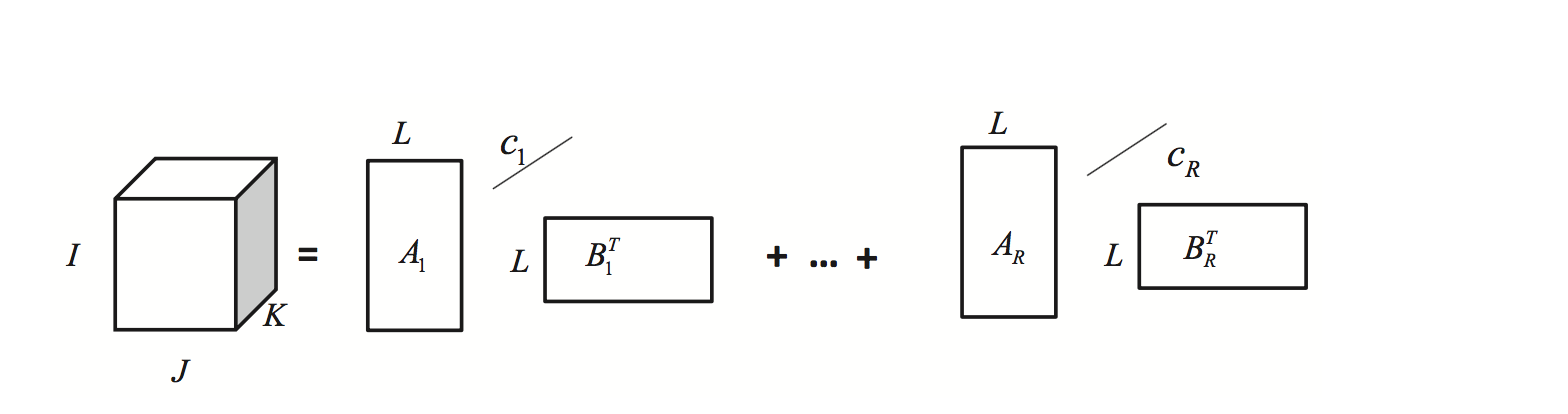
$Rank-(L_{r}, L_{r}, 1) 分解算法$ 。

Rank- $(L, L, 1)$ 分解

当 $Rank−(Lr,Lr,1)\text{Rank}-(L_{r}, L_{r}, 1)$ 的每一个 $L_{r}$ 取值为一致，即 $L$ 时，即可得到 $Rank−(L,L,1)\text{Rank}-(L, L, 1)$ 分解，即：

Rank-(L, L, 1) 分解。

BTD 分解的应用

BTD 分解的现阶段主要应用在盲源分离上，尤其是它的蜕化形式 $Rank−(L,L,1)\text{Rank}-(L, L, 1)$ 形式。在 $Rank−(L,L,1)\text{Rank}-(L, L, 1)$ 中， $c_{r}$ 可以看作是一个信号， $Ar×BrA_{r} \times B_{r}$ 可以看作是混合矩阵的低秩表达形式。本人也基于此分解在 IEEE TGRS 上发表了一篇题为 “Matrix-Vector Nonnegative Tensor Factorization for Blind Unmixing of Hyperspectral Imagery” 的文章，具体可以参考 http://www.cs.zju.edu.cn/people/qianyt/paper/Matrix-Vector%20Nonnegative%20Tensor%20Factorization%20for%20Blind%20Unmixing%20of%20Hyperspectral%20Imagery.pdf。

此外，BTD 分解现在也开始应用在深度学习中（事实上，张量分解在深度学习中的应用最近被广泛研究，因为张量分解可以有效地减少深度学习中参数的个数，具体可以参考相关文献）。新加坡国立大学颜水成教授 2017 年发表了一篇题为 Sharing Residual Units Through Collective Tensor Factorization in Deep Neural Networks 的文章，这篇文章中，用 BTD 分解来代替残差网络中的卷积单元（尚未仔细阅读，待详细研究后补充）：

Figure 1. Convolution kernel approximation by different approaches.
图 1. 不同方法的卷积核近似。

(a) A full rank convolution layer with a kernel size of $\times h$ .
一个具有 $\times h$ 核大小的全秩卷积层。

(b) An approximation of (a) by using the low-rank Tucker Decomposition (a special case of Block Term Decomposition when $R = 1$ ).
使用低秩 Tucker 分解（当 $R = 1$ 时，块项分解的特例）对 (a) 进行近似。

© An approximation of (a) by using low-rank Block Term Decomposition. The new proposed CRU shares the first two layers (yellow) across different residual functions.
使用低秩块项分解对 (a) 进行近似。新提出的 CRU 在不同的残差函数中共享前两层（黄色）。

via：

张量分解-张量介绍
https://www.xiongfuli.com/机器学习/2016-06/tensor-decomposition-part1.html
张量分解-CP分解
https://www.xiongfuli.com/机器学习/2016-06/tensor-decomposition-cp.html
张量分解-Tucker分解
https://www.xiongfuli.com/机器学习/2016-06/tensor-decomposition-tucker.html
张量分解-Block term decomposition (BTD)
https://www.xiongfuli.com/机器学习/2017-06/tensor-decomposition-BTD.html

查看全文

http://www.dtcms.com/a/446154.html