LeetCode 分类刷题：74. 搜索二维矩阵

题目

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

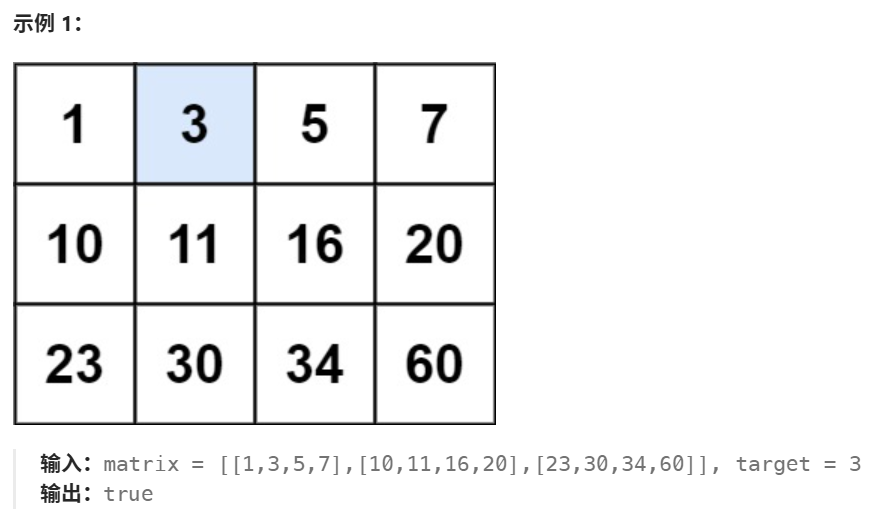
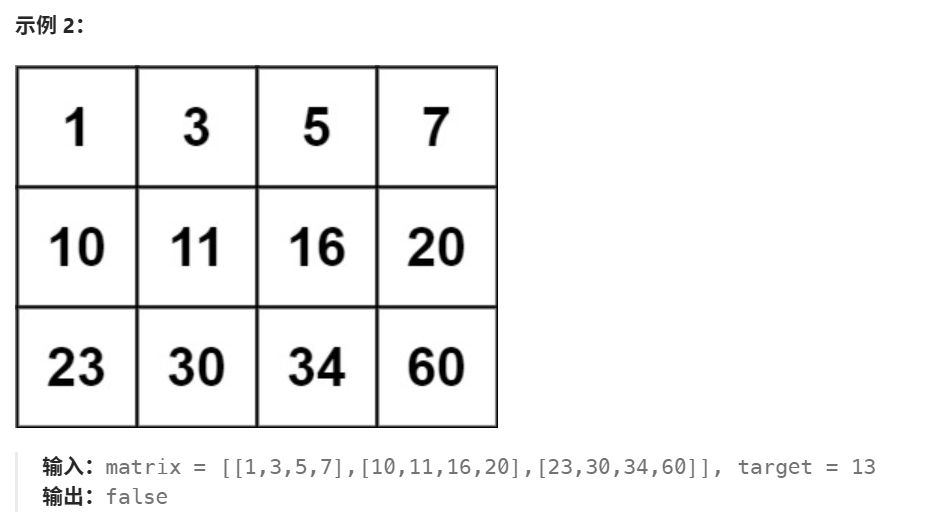
给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

解析

由于矩阵的每一行是递增的，且每行的第一个数大于前一行的最后一个数，如果把矩阵每一行拼在一起，我们可以得到一个递增数组。

例如示例 1，三行拼在一起得

a=[1,3,5,7,10,11,16,20,23,30,34,60]
由于这是一个有序数组，我们可以用二分查找判断 target 是否在 matrix 中。

一般地，有

• a[i]=matrix[ ⌊i/n⌋ ][ i mod n ]

作者：灵茶山艾府
链接：https://leetcode.cn/problems/search-a-2d-matrix/submissions/668071757/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

答案

自己写的

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:row = len(matrix)col = len(matrix[0])for i in range(row):    # 遍历每一行，进行二分查找left = -1right = col - 1if matrix[i][right] < target:    # 当前行最大值小于target，直接跳至下一行continuewhile left + 1 < right:mid = (left + right) // 2if matrix[i][mid] < target:    # left恒小于target，right恒大于等于targetleft = midelse:right = midif matrix[i][right] == target:    # right指向第一个大于等于target元素return Truereturn False

灵神答案

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:m, n = len(matrix), len(matrix[0])left, right = -1, m * nwhile left + 1 < right:mid = (left + right) // 2x = matrix[mid // n][mid % n]if x == target:return Trueif x < target:    # left恒指向小于target的元素，right恒指向大于target的元素left = mid    # target的搜索范围为开区间(left, right)else:right = mid return False

复杂度分析

我的答案：

时间复杂度：O(mlog(n))，其中 m 和 n 分别为 matrix 的行数和列数。

空间复杂度：O(1)。

灵神答案：

时间复杂度：O(log(mn))，其中 m 和 n 分别为 matrix 的行数和列数。

空间复杂度：O(1)。

作者：灵茶山艾府
链接：https://leetcode.cn/problems/search-a-2d-matrix/submissions/668071757/
来源：力扣（LeetCode）