算法题（226）：L国的战斗之间谍

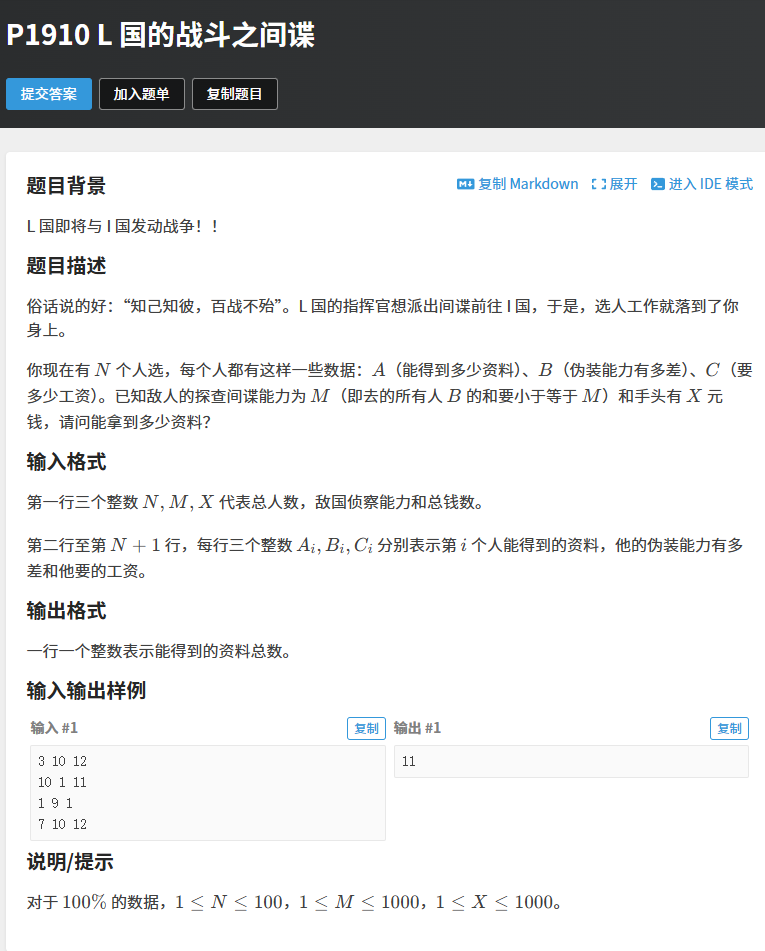
审题：
本题需要我们解决多重限制条件的01背包问题

思路：
方法一：动态规划

本题的每种物品相当于只有一个（01背包），限制条件有两个分别是伪装能力总合小于等于m，消耗钱数小于等于x

（1）状态表示：
f[i][j][k]表示从前i个人中找，在伪装能力总合小于等于m，且总耗费钱数小于等于x的前提下所得到的最多资料

（2）状态转移方程：
情况1：选择第i个人

情况2：不选择第i个人

（3）初始化：

全初始化为0即可

（4）填表顺序：
由于当前节点求值依赖于上一行的节点，所以我们填表的纵向顺序必须是从小到大

（5）答案输出：
直接输出f[n][m][x]即可

（6）空间优化：
由于不进行空间优化会导致超出空间上限，所以这里我们对第一个参数进行优化。

将它从三维降到二维，然后将第二，三层循环的遍历顺序修改为从大到小（防止数据覆盖导致计算出错）

解题：
 

//#include<iostream>
//using namespace std;
//const int N = 110, M = 1010;
//int n, m, x;
//int a[N], b[N], c[N];
//int f[N][M][M];//f[i][j][k]表示从前i个人中找，在伪装能力总合小于等于m，且总耗费钱数小于等于x的前提下所得到的最多资料
//int main()
//{
//	cin >> n >> m >> x;
//	for (int i = 1; i <= n; i++)
//	{
//		cin >> a[i] >> b[i] >> c[i];
//	}
//	//填表
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= m; j++)
//		{
//			for (int k = 1; k <= x; k++)
//			{
//				f[i][j][k] = f[i - 1][j][k];
//				if (j >= b[i] && k >= c[i])
//				{
//					f[i][j][k] = max(f[i][j][k], f[i - 1][j - b[i]][k - c[i]] + a[i]);
//				}
//			}
//		}
//	}
//	//答案输出
//	cout << f[n][m][x] << endl;
//	return 0;
//}
#include<iostream>
using namespace std;
const int N = 110, M = 1010;
int n, m, x;
int a[N], b[N], c[N];
int f[M][M];//f[i][j][k]表示从前i个人中找，在伪装能力总合小于等于m，且总耗费钱数小于等于x的前提下所得到的最多资料
int main()
{cin >> n >> m >> x;for (int i = 1; i <= n; i++){cin >> a[i] >> b[i] >> c[i];}//填表for (int i = 1; i <= n; i++){for (int j = m; j >= b[i]; j--){for (int k = x; k >= c[i]; k--){f[j][k] = max(f[j][k], f[j - b[i]][k - c[i]] + a[i]);}}}//答案输出cout << f[m][x] << endl;return 0;
}

被注释的是非空间优化版本，后面的是空间优化版本

P1910 L 国的战斗之间谍 - 洛谷