近世代数(抽象代数)详细笔记--群
近世代数研究的对象就是具有代数运算的集合,这样的集合称为“代数系”
代数系的更确切定义是指一个非空集合 A,连同定义在 A 上的若干个满足特定规则(如封闭性、结合律等)的代数运算,所构成的整体。
第一章:群
1.1等价关系和集合的分类
定义–关系
设SSS是一个非空集合,R\mathcal{R}R是关于SSS的元素的一个条件. 如果对SSS中任意一个有序元素对(a,b)(a,b)(a,b),我们总能确定aaa与bbb是否满足条件R\mathcal{R}R,就称R\mathcal{R}R是SSS的一个关系(relation). 如果aaa与bbb满足条件R\mathcal{R}R,则称aaa与bbb有关系R\mathcal{R}R,记作aRba\mathcal{R}baRb;否则称aaa与bbb无关系R\mathcal{R}R. 关系R\mathcal{R}R也称为二元关系.
eg. 在整数集Z\mathbb{Z}Z中,整除是关系。(∀a,b∈Z\forall a,b \in \mathbb{Z}∀a,b∈Z,要么a∣ba\mid ba∣b,要么a∤ba\nmid ba∤b)
理解:关系是集合中元素相互联系的方式,可以用有序对表示,关系可以有很多种性质,如自反性,对称性,传递性等。
关系的本质是有序对的集合:如果有一个集合SSS,那么一个关系R\mathcal{R}R可以看作是S×SS \times SS×S(即SSS与自身的笛卡尔积)的一个子集。也就是说,R⊆S×S\mathcal{R} \subseteq S \times SR⊆S×S,其中每个有序对(a,b)(a,b)(a,b)表示aaa和bbb满足关系R\mathcal{R}R(即aRba\mathcal{R}baRb)。
定义–等价关系
同时具有自反性,对称性,传递性的关系叫做等价关系
设 R\mathcal{R}R 是非空集合 SSS 的一个关系,如果 R\mathcal{R}R 满足
- 自反性,即对任意的 a∈Sa \in Sa∈S,有 aRa;a\mathcal{R}a;aRa;
- 对称性,即若 aRba\mathcal{R}baRb,则 bRab\mathcal{R}abRa;
- 传递性,即若 aRba\mathcal{R}baRb,且 bRcb\mathcal{R}cbRc,则 aRca\mathcal{R}caRc
则称 R\mathcal{R}R 是 SSS 的一个等价关系 (equivalence relation),并且如果 aRba\mathcal{R}baRb,则称 aaa 等价于 bbb,记作 a∼ba \sim ba∼b
目的:研究等价关系的目的在于将集合中的元素进行分类,选取没类元素的 代表元素来件地问题的复杂度。如软件测试时,可利用等价类来选择测试用例。
eg:同余关系是等价关系
设mmm是正整数,在整数集Z\mathbb{Z}Z中,规定
aRb⟺m∣a−b,∀a,b∈Z,a\mathcal{R}b \iff m \mid a - b, \ \forall a,b \in \mathbb{Z},aRb⟺m∣a−b, ∀a,b∈Z,
(1) 对任意整数aaa,有m∣a−am \mid a - am∣a−a;
(2) 若m∣a−bm \mid a - bm∣a−b,则m∣b−am \mid b - am∣b−a;
(3) 若m∣a−bm \mid a - bm∣a−b,m∣b−cm \mid b - cm∣b−c,则m∣a−cm \mid a - cm∣a−c,
所以R\mathcal{R}R是Z\mathbb{Z}Z的一个等价关系。显然aaa与bbb等价当且仅当aaa与bbb被mmm除有相同的余数,因此称这个关系为同余关系(congruence relation),并记作a≡b(mod m)a \equiv b \ (\text{mod} \ m)a≡b (mod m)。
定义–划分
如果非空集合SSS是它的某些两两不相交的非空子集的并,则称这些子集为集合SSS的一种划分(partition),其中每个子集称为SSS一个类(class)。如果SSS的子集族{Si∣i∈I}\{S_i \mid i \in I\}{Si∣i∈I}构成SSS的一种划分,则记作P={Si∣i∈I}\mathcal{P} = \{S_i \mid i \in I\}P={Si∣i∈I}。
由此定义可知,集合SSS的子集族{Si∣i∈I}\{S_i \mid i \in I\}{Si∣i∈I}构成SSS的一种划分当且仅当
- S=⋃i∈ISiS = \bigcup_{i \in I} S_iS=⋃i∈ISi;
- Si∩Sj=∅,i≠jS_i \cap S_j = \varnothing, i \neq jSi∩Sj=∅,i=j.
理解:用刀切蛋糕,蛋糕的每一块彼此独立(无公共元素),所有块蛋糕合起来又是完整的蛋糕
注:等价关系和划分是一一对应的(一个等价关系预示着一个划分方式,一个划分方式包含着一个等价关系)
定义–等价类,商集
如果∼\sim∼是集合SSS的一个等价关系,对a∈Sa \in Sa∈S,令
[a]={x∈S∣x∼a}.[a] = \{x \in S \mid x \sim a\}.[a]={x∈S∣x∼a}.
称子集[a][a][a]为SSS的一个等价类(equivalence class)。SSS的全体等价类的集合称为集合SSS在等价关系下的商集(quotient set),记S/∼S/\simS/∼。
理解:商集本身是集合其里面的元素也是集合
模6的等价类
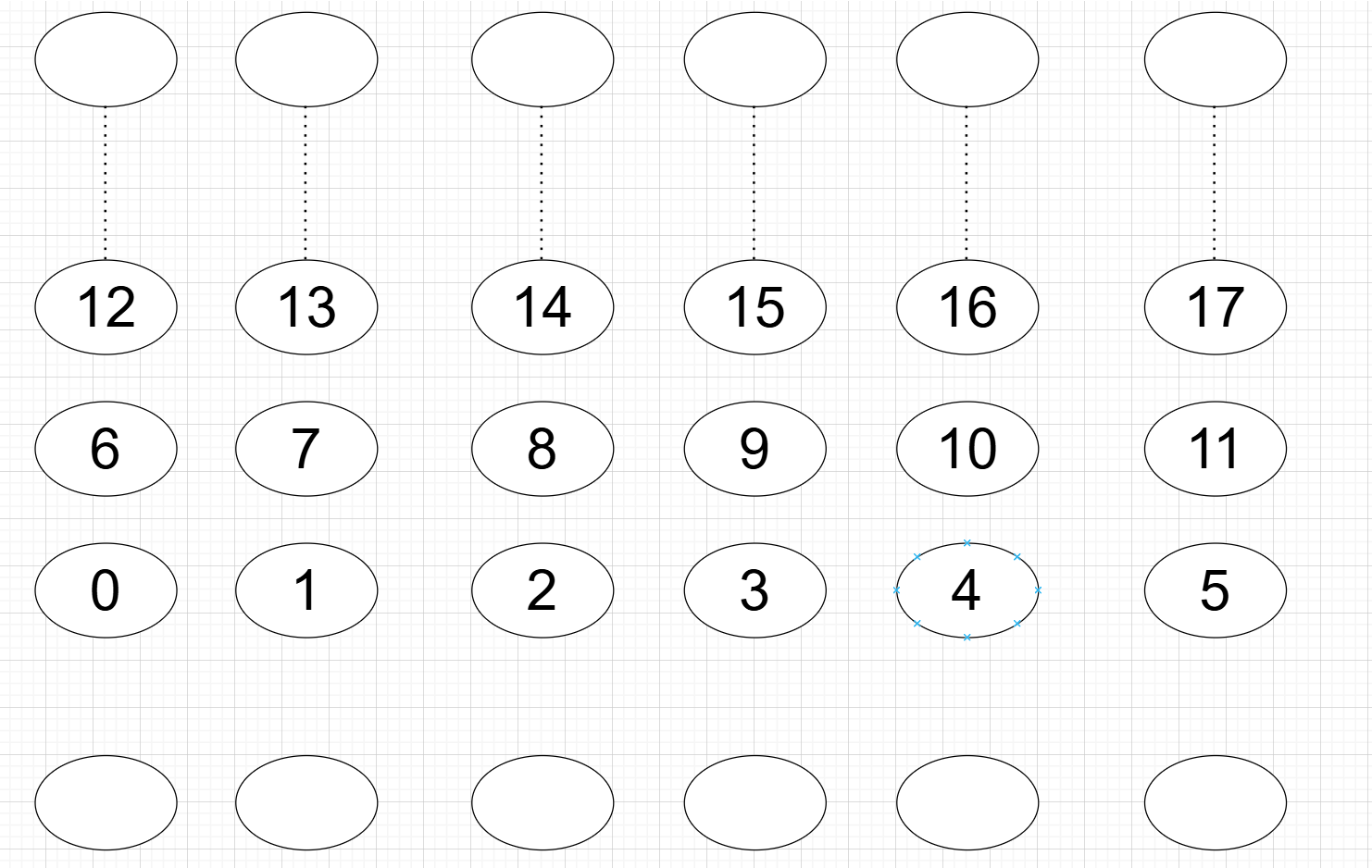
等价关系把集合划分为了等价类
如果集合SSS具有代数结构(如群、环、向量空间),并且等价关系∼\sim∼与该结构兼容(即运算在等价类上良定义),则商集S/∼S/\simS/∼可以继承相同的结构
1.2群的概念
定义–代数运算
设AAA是一个非空集合,若对AAA中任意两个元素a,ba,ba,b,通过某个法则“⋅\cdot⋅”,有AAA中唯一确定的元素ccc与之对应,则称法则“⋅\cdot⋅”为集合AAA上的一个代数运算(algebraic operation)。元素ccc是a,ba,ba,b通过运算“⋅\cdot⋅”作用的结果,将此结果记为a⋅b=ca \cdot b = ca⋅b=c。
性质:代数运算一定满足封闭性
定义–群

设GGG是一个非空集合,“⋅\cdot⋅”是GGG上的一个代数运算,即对所有的a,b∈Ga,b \in Ga,b∈G,有a⋅b∈Ga \cdot b \in Ga⋅b∈G。如果GGG的运算还满足
-
结合律,即对所有的a,b,c∈Ga,b,c \in Ga,b,c∈G,有(a⋅b)⋅c=a⋅(b⋅c)(a \cdot b) \cdot c = a \cdot (b \cdot c)(a⋅b)⋅c=a⋅(b⋅c);
-
GGG中有元素eee(单位元),使对每个a∈Ga \in Ga∈G,有e⋅a=a⋅e=ae \cdot a = a \cdot e = ae⋅a=a⋅e=a;
-
对GGG中每个元素aaa,存在元素b∈Gb \in Gb∈G,使a⋅b=b⋅a=ea \cdot b = b \cdot a = ea⋅b=b⋅a=e,
则称GGG关于运算“⋅\cdot⋅”构成一个群(group),记作(G,⋅)(G, \cdot)(G,⋅)。也称GGG为群。
性质:
- 群GGG的单位元是唯一的
- 群GGG的每个元素的逆元是唯一的
- 对∀a∈G\forall a \in G∀a∈G,有(a−1)−1=a(a^{-1})^{-1}=a(a−1)−1=a
- 对∀a,b∈G\forall a,b \in G∀a,b∈G,有(ab)−1=b−1a−1(ab)^{-1}=b^{-1}a^{-1}(ab)−1=b−1a−1
- 在群中消去律成立,即:设a,b,c∈Ga,b,c \in Ga,b,c∈G,若ab=acab=acab=ac或ba=caba=caba=ca,则b=cb=cb=c
- 无零元
- 除e之外没有幂等元素
- ax=bax=bax=b,ya=bya=bya=b在群中有唯一解
常见的非交换群:
n 阶一般线性群 GL(n, ℝ):所有 n×n 的可逆实矩阵在矩阵乘法下构成的群。
对称群SnS_nSn:当n≥3n\geq3n≥3时为非交换群,n=1,2n=1,2n=1,2时是交换群
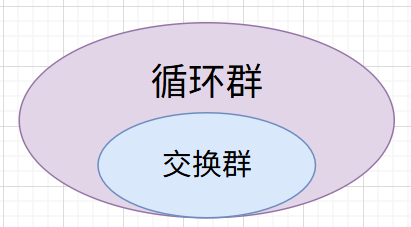
定义–交换群

群GGG的运算满足交换律,即对任意的a,b∈Ga,b \in Ga,b∈G,有a⋅b=b⋅aa \cdot b = b \cdot aa⋅b=b⋅a,则称GGG是一个交换群(commutative group) 或阿贝尔群(Abelian group)。
常见的交换群:
1.循环群:所有的循环群都是交换群
2.数系加法群
- 整数加法群(Z,+)(\mathbb{Z}, +)(Z,+):所有整数在加法运算下构成群。单位元是000,任意整数nnn的逆元是−n-n−n。
- 有理数加法群(Q,+)(\mathbb{Q}, +)(Q,+):所有有理数在加法下构成群。
- 实数加法群(R,+)(\mathbb{R}, +)(R,+):所有实数在加法下构成群。
- 复数加法群(C,+)(\mathbb{C}, +)(C,+):所有复数在加法下构成群。
3.数系加群对应的模nnn的剩余类加群
4.数系乘法群(非零元素)
注意:这些数系在乘法下不能构成群,因为 000 没有乘法逆元。但如果我们只考虑非零元素,它们就构成交换群。
-
非零有理数乘法群 (Q∗,⋅)(\mathbb{Q}^\ast, \cdot)(Q∗,⋅):单位元是111,有理数 a/ba/ba/b 的逆元是 b/ab/ab/a。
-
非零实数乘法群 (R∗,⋅)(\mathbb{R}^\ast, \cdot)(R∗,⋅)
-
非零复数乘法群 (C∗,⋅)(\mathbb{C}^\ast, \cdot)(C∗,⋅)
5.模 ppp(素数)的非零剩余类乘法群 (Zp∗,⋅)(\mathbb{Z}_p^\ast, \cdot)(Zp∗,⋅):这是一个非常重要的有限交换群。例如,(Z5∗,⋅)(\mathbb{Z}_5^\ast, \cdot)(Z5∗,⋅) 的集合是 {1,2,3,4}\{1, 2, 3, 4\}{1,2,3,4},因为 000 被排除。2⋅3=6≡1(mod 5)2 \cdot 3 = 6 \equiv 1 \ (\text{mod} \ 5)2⋅3=6≡1 (mod 5),所以 222 和 333 互为逆元。
定义–群的阶
群GGG中元素的个数称为群GGG的阶(order),记为∣G∣|G|∣G∣。如果∣G∣|G|∣G∣是有限数,则称GGG为有限群(finite group),否则称GGG为无限群(infinite group)。
定义–群元素的方幂and倍数
乘法群中可以定义群的元素的方幂:
对任意的正整数 ( n ),定义
an=a⋅a⋯a⏟n个aa^n = \underbrace{a \cdot a \cdots a}_{n个a}an=n个aa⋅a⋯a,
再约定
a0=ea^0 = ea0=e,
a−n=(a−1)n(n为正整数)a^{-n} = (a^{-1})^n \ (n \text{ 为正整数})a−n=(a−1)n (n 为正整数),
则 ana^nan对任意整数 nnn 都有意义,并且对任意的a∈G,m,n∈Za \in G, m, n \in \mathbb{Z}a∈G,m,n∈Z,有以下指数法则:
- an⋅am=an+ma^n \cdot a^m = a^{n+m}an⋅am=an+m;
- (an)m=anm(a^n)^m = a^{nm}(an)m=anm;
- 若 ( G ) 是交换群,则 (ab)n=anbn(ab)^n = a^n b^n(ab)n=anbn;若 ( G ) 不是交换群,则 (ab)n=anbn(ab)^n = a^n b^n(ab)n=anbn 一般不成立。
加群中定义元素的倍数
当 ( G ) 是加群时,元素的“方幂”改写为倍数:
na=a+a+⋯+a⏟n个ana = \underbrace{a + a + \cdots + a}_{n个a}na=n个aa+a+⋯+a,
同时约定
0a=00a = 00a=0,
(−n)a=n(−a)(-n)a = n(-a)(−n)a=n(−a),
相应地,指数法则变为倍数法则:
- na+ma=(n+m)ana + ma = (n + m)ana+ma=(n+m)a;
- m(na)=(mn)am(na) = (mn)am(na)=(mn)a;
- n(a+b)=na+nbn(a + b) = na + nbn(a+b)=na+nb(因为加群是交换群,所以该式总是成立的)。
定理:群的判定1
G是一个具有代数运算的非空集合,则G为群⇔\Leftrightarrow⇔
- G的运算满足结合律
- 左单位元:∀a∈G,\forall a \in G ,∀a∈G,有ea=aea=aea=a
- 左逆元:∀a∈G\forall a\in G∀a∈G,$\exist a’\in G $ s.t.a′a=ea'a=ea′a=e(e为左单位元)
定理:群的判定2
设GGG是一个具有乘法运算且满足结合律的非空集合,则GGG是群⇔\Leftrightarrow⇔
对∀a,b∈G\forall a,b \in G∀a,b∈G,方程aX=baX=baX=b与Ya=bYa=bYa=b在GGG中有解
1.3子群
定义–子群
设GGG是一个群,HHH是GGG的一个非空子集。如果HHH关于GGG的运算也构成群,则称HHH为GGG的一个子群(subgroup),记作H<GH < GH<G。
PS: 对任意群GGG,GGG本身以及只含单位元eee的子集H={e}H = \{e\}H={e} 是GGG的子群,这两个子群称为GGG的平凡子群(trivial subgroup)。群GGG的其他子群称为GGG的非平凡子群(nontrivial subgroup);群GGG的不等于它自身的子群称为GGG的真子群(proper subgroup)。
定理–1.3.1群与子群元素关系
设GGG为群,HHH是GGG的子群,则
(1) 群GGG的单位元eee是HHH的单位元;
(2) 对任意的a∈Ha \in Ha∈H,aaa在GGG中的逆元a−1a^{-1}a−1就是aaa在HHH中的逆元。
定理–1.3.2子群的判定1
设GGG为群,HHH是群GGG的非空子集,则HHH成为群GGG的子群的充分必要条件是
(1) 对任意a,b∈Ha,b \in Ha,b∈H,有ab∈Hab \in Hab∈H;
(2) 对任意a∈Ha \in Ha∈H,有a−1∈Ha^{-1} \in Ha−1∈H。
定理–1.3.3子群的判定2
设GGG为群,HHH是群GGG的非空子集,则HHH成为GGG的子群的充分必要条件是对任意的a,b∈Ha,b \in Ha,b∈H,有ab−1∈Hab^{-1} \in Hab−1∈H。
定理–1.3.4子群的运算性质
群GGG的任意两个子群的交集还是GGG的子群。
注:G的$\forall 子群的并不一定是子群的并不一定是子群的并不一定是G$的子群
定义–生成子群
设SSS是群GGG的一个非空子集,令MMM表示GGG中所有包含SSS的子群所组成的集合,即 M={H<G∣S⊆H}.M = \{ H < G \mid S \subseteq H \}.M={H<G∣S⊆H}. GGG本身显然包含SSS,所以G∈MG \in MG∈M,从而MMM非空。令 K=⋂H∈MH,K = \bigcap\limits_{H \in M} H,K=H∈M⋂H, 则KKK是GGG的子群,称KKK为群GGG的由子集SSS所生成的子群(简称生成子群),记作⟨S⟩\langle S \rangle⟨S⟩,即 ⟨S⟩=⋂S⊆H<GH,\langle S \rangle = \bigcap\limits_{S \subseteq H < G} H,⟨S⟩=S⊆H<G⋂H, 子集SSS称为⟨S⟩\langle S \rangle⟨S⟩的生成元组。 若S={a1,a2,⋯,ar}S = \{ a_1, a_2, \cdots, a_r \}S={a1,a2,⋯,ar}为有限集,则记 ⟨S⟩=⟨a1,a2,⋯,ar⟩.\langle S \rangle = \langle a_1, a_2, \cdots, a_r \rangle.⟨S⟩=⟨a1,a2,⋯,ar⟩.
**理解:**群中某些元素所生成的最小子群
定理–1.3.5
设SSS是GGG的非空子集,则
-
⟨S⟩\langle S \rangle⟨S⟩是GGG的包含SSS的最小子群;
-
⟨S⟩={a1l1a2l2⋯aklk∣ai∈S,li=±1,k∈N}\langle S \rangle = \{ a_1^{l_1} a_2^{l_2} \cdots a_k^{l_k} \mid a_i \in S, l_i = \pm 1, k \in \mathbb{N} \}⟨S⟩={a1l1a2l2⋯aklk∣ai∈S,li=±1,k∈N}
PS:当SSS只包含群GGG的一个元素aaa时,由于 al1al2⋯alk=a∑i=1kli,a^{l_1}a^{l_2}\cdots a^{l_k}=a^{\sum_{i=1}^k l_i},al1al2⋯alk=a∑i=1kli, 所以 ⟨a⟩={ar∣r∈Z}.\langle a \rangle = \{ a^r \mid r \in \mathbb{Z} \}.⟨a⟩={ar∣r∈Z}. 这种由一个元素aaa生成的子群称为由aaa生成的循环群(cyclic group)。
**理解:**群中某个元素所生成的最小子群
1.4群的同构
韩老师的引言很不错:

定义–映射类型
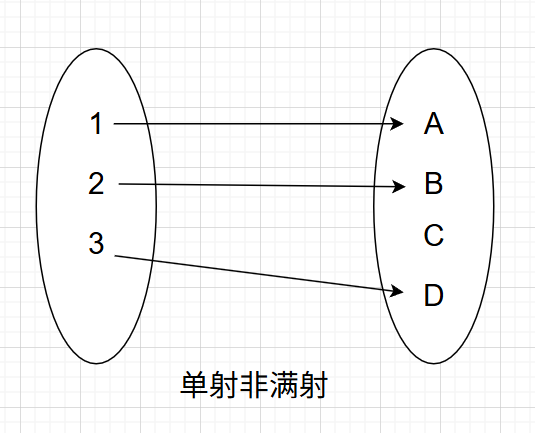
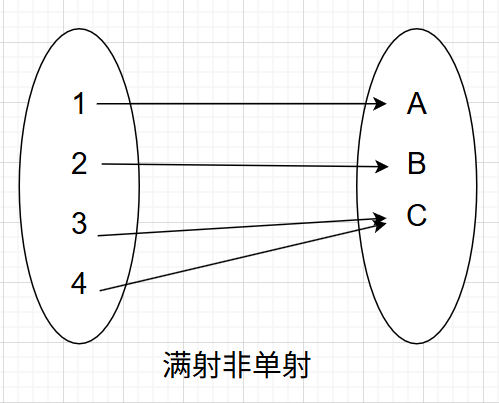
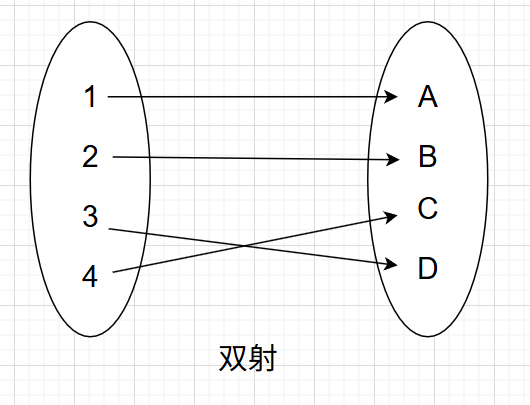
- 映射(function):每一个xxx都有唯一的yyy与之对应;
- 单射(injection):不同的x必须映射到不同的y(但是每一个x都得能够映射到Y中)
- 满射(surjection):每一个yyy都必有至少一个xxx与之对应;
- 双射(bijection):每一个xxx都有唯一的yyy与之对应,每一个yyy都有唯一的xxx与之对应。
理解:
- 单射就是一个萝卜一个坑,有的坑有可能没萝卜;
- 满射就是所有坑都有萝卜,有的坑可能有不止一个萝卜;
- 双射就是严格的一个萝卜一个坑,一个坑一个萝卜,所有萝卜都有坑,所有坑都有萝卜。
定义–同构与自同构
设(G,.)(G,.)(G,.)与(G′,∗)(G',*)(G′,∗)是两个群,ϕ\phiϕ是GGG到G′G'G′的一一对应,使
ϕ(a⋅b)=ϕ(a)∗ϕ(b),∀a,b∈G,\phi(a \cdot b) = \phi(a) * \phi(b), \quad \forall a,b \in G,ϕ(a⋅b)=ϕ(a)∗ϕ(b),∀a,b∈G,
则称ϕ\phiϕ为群GGG到G′G'G′的一个同构映射(isomorphism),简称同构,并称群GGG与G′G'G′同构(isomorphic),记作
ϕ:G≅G′.\phi: G \cong G'.ϕ:G≅G′.
群GGG到它自身的同构映射称为群GGG的自同构(automorphism)。
自同构的密码学运用举例 对称加密的核心是 “加密和解密使用同一密钥”,而自同构的 “可逆性” 和 “结构保持性” 恰好匹配这一需求: - 加密过程可视为 “自同构映射”:将明文(某一数学结构中的元素)通过密钥控制的自同构映射为密文(保持结构的 “不可读性”,但可逆); - 解密过程即 “自同构的逆映射”:用同一密钥还原密文为明文。 - **例:AES 加密算法**:AES 的核心变换 “字节代换(SubBytes)” 本质是有限域$GF(2^8)$ 上的自同构(保持有限域的加法和乘法运算),“行移位(ShiftRows)”“列混合(MixColumns)” 则是线性空间的自同构 —— 这些自同构的组合确保了加密的 “雪崩效应”(明文或密钥微小变化导致密文大幅变化),保障了加密安全性。证明:群同构的步骤:
要证明两个群 GGG 和 G′G'G′ 同构,通常需要构造一个双射 ϕ:G→G′\phi: G \to G'ϕ:G→G′,并且证明 ϕ\phiϕ 保持群运算。具体步骤如下:
第一步 构作群 GGG 与群 G′G'G′ 的元素间的对应关系 ϕ\phiϕ,并证明 ϕ\phiϕ 是 GGG 到 G′G'G′ 的映射;
第二步 证明 ϕ\phiϕ 是 GGG 到 G′G'G′ 的单映射。即对任意的 x,y∈Gx,y \in Gx,y∈G,证明由 ϕ(x)=ϕ(y)\phi(x)=\phi(y)ϕ(x)=ϕ(y) 可推出 x=yx=yx=y;
第三步 证明 ϕ\phiϕ 是 GGG 到 G′G'G′ 的满映射。即对任意的 x′∈G′x' \in G'x′∈G′,证明存在 x∈Gx \in Gx∈G,使 ϕ(x)=x′\phi(x)=x'ϕ(x)=x′;
第四步 证明 ϕ\phiϕ 保持运算。即对任意的 x,y∈Gx,y \in Gx,y∈G,证明 ϕ(xy)=ϕ(x)ϕ(y)\phi(xy)=\phi(x)\phi(y)ϕ(xy)=ϕ(x)ϕ(y)。
定理1.4.1群同构的性质
设ϕ\phiϕ是群GGG到G′G'G′的同构映射,eee与e′e'e′分别是GGG与G′G'G′的单位元,aaa是GGG的任一元素,则
(1) ϕ(e)=e′\phi(e)=e'ϕ(e)=e′;
(2) ϕ(a−1)=(ϕ(a))−1\phi(a^{-1})=(\phi(a))^{-1}ϕ(a−1)=(ϕ(a))−1;
(3) ϕ\phiϕ是可逆映射,且ϕ\phiϕ的逆映射ϕ−1\phi^{-1}ϕ−1是群G′G'G′到群GGG的同构映射。
理解:群同构把单位元映射为单位元,逆元映射为逆元
PS:设群GGG与G′G'G′同构。如果GGG是交换群,则G′G'G′也是交换群;如果GGG是有限群,则G′G'G′也是有限群,且∣G∣=∣G′∣|G| = |G'|∣G∣=∣G′∣。
定理:1.4.2群同构是等价关系
群的同构是一个等价关系,即
(1) G≅GG \cong GG≅G(反身性);
(2) 若G≅G′G \cong G'G≅G′,则G′≅GG' \cong GG′≅G(对称性);
(3) 若G≅G′G \cong G'G≅G′,G′≅G′′G' \cong G''G′≅G′′,则G≅G′′G \cong G''G≅G′′(传递性), 其中G,G′,G′′G, G', G''G,G′,G′′都是群。
理解:同构的群具有完全相同的群性质
定义:对称群和变换群
对于非空集合XXX,全体可逆变换(即XXX到自身的双射变换)关于“变换的合成”(即依次进行两个变换的运算)所构成的群,称为集合XXX的对称群(记为SXS_XSX);而$S_X 的任意一个子群,就称为的任意一个子群,就称为的任意一个子群,就称为X$的一个变换群。
定理:凯莱定理
每一个群都同构于一个变换群
1.5循环群
定义:元素的阶
设GGG是一个群,eee是GGG的单位元,a∈Ga\in Ga∈G。如果存在正整数rrr,使ar=ea^r=ear=e,则称aaa是有限阶的,否则称aaa是无限阶的。使ar=ea^r=ear=e的最小正整数rrr称为元素aaa的阶(order),记作orda=r\text{ord}\,a = rorda=r。如果aaa是无限阶的,则记作orda=∞\text{ord}\,a = \inftyorda=∞。
定理:关于元素阶的性质
设GGG为群,eee为GGG的单位元。
(1) 对任意的a∈Ga \in Ga∈G,有orda=orda−1\text{ord}\,a = \text{ord}\,a^{-1}orda=orda−1;
(2) 设orda=n\text{ord}\,a = norda=n,如果有m∈Zm \in \mathbb{Z}m∈Z,使am=ea^m = eam=e,则n∣mn \mid mn∣m;
(3) 设orda=n\text{ord}\,a = norda=n,则对任意的m∈Zm \in \mathbb{Z}m∈Z,ordam=n(n,m)\text{ord}\,a^m = \frac{n}{(n, m)}ordam=(n,m)n;
(4) 设orda=n\text{ord}\,a = norda=n,ordb=m\text{ord}\,b = mordb=m,如果ab=baab = baab=ba,且gcd(n,m)=1\gcd(n, m) = 1gcd(n,m)=1,则ord(ab)=mn\text{ord}\,(ab) = mnord(ab)=mn。
定理:元素的阶与群的阶之间的关系
设GGG是一个有限群,∣G∣=n|G|=n∣G∣=n,则对任意的a∈Ga \in Ga∈G,aaa是有限阶的,且orda∣∣G∣\text{ord}\,a \mid |G|orda∣∣G∣,即一个有限群的任一个元素的阶都是群阶数的因子。
定义:循环群
设GGG是群,如果存在a∈Ga \in Ga∈G,使得G=⟨a⟩G = \langle a \rangleG=⟨a⟩,则称GGG为一个循环群(cyclic group),并称aaa为GGG的一个生成元(generator)。当GGG的元素个数无限时,称GGG为无限循环群;当GGG的元素个数为nnn时,称GGG为**nnn阶循环群**。
性质:循环群的性质
(1) (a−1)=⟨a⟩(a^{-1}) = \langle a \rangle(a−1)=⟨a⟩;
(2) 如果GGG是有限群,则G=⟨a⟩⟺∣G∣=ordaG = \langle a \rangle \iff |G| = \text{ord}\,aG=⟨a⟩⟺∣G∣=orda;
(3) 如果GGG为无限循环群,则 G={e,a,a−1,a2,a−2,a3,a−3,…}G = \{e, a, a^{-1}, a^2, a^{-2}, a^3, a^{-3}, \dots\}G={e,a,a−1,a2,a−2,a3,a−3,…}, 且对任意的k,l∈Zk, l \in \mathbb{Z}k,l∈Z,由ak=ala^k = a^lak=al,必可推出k=lk = lk=l;
(4) 如果GGG为nnn阶循环群,则 G={e,a,a2,a3,…,an−1}G = \{e, a, a^2, a^3, \dots, a^{n-1}\}G={e,a,a2,a3,…,an−1}, 且对任意的k,l∈Zk, l \in \mathbb{Z}k,l∈Z, ak=al⟺n∣k−la^k = a^l \iff n \mid k - lak=al⟺n∣k−l
定理:原根定理
设ppp为素数,则Zp∗\mathbb{Z}_p^*Zp∗是p−1p - 1p−1阶循环群。
理解:设ppp是一个素数,则模ppp的乘法群Zp∗\mathbb{Z}_p^*Zp∗(即集合{1,2,…,p−1}\{1, 2, \dots, p - 1\}{1,2,…,p−1}在模ppp乘法下构成的群)是一个阶为p−1p - 1p−1的循环群。
在素数乘法群中原根和生成元是一回事
定理:生成元的个数
设G=⟨a⟩G = \langle a \rangleG=⟨a⟩为循环群,则
(1) 如果∣G∣=∞|G| = \infty∣G∣=∞,则aaa与a−1a^{-1}a−1是GGG的两个仅有的生成元;
(2) 如果∣G∣=n|G| = n∣G∣=n,则GGG恰有φ(n)\varphi(n)φ(n)个生成元,且ara^rar是GGG的生成元的充分必要条件是(n,r)=1(n, r) = 1(n,r)=1,其中φ(n)\varphi(n)φ(n)是欧拉函数。
理解:
生成元的作用是“生成”整个群,即通过重复应用群运算(乘法或加法)可以得到群的所有元素。 如果rrr和nnn 有公因子,那么ara^rar生成的子群只会是GGG的一个真子群,无法覆盖整个GGG。 只有当rrr和 nnn互质时,ara^rar 的幂才能遍历所有 nnn个元素。如果不互质会陷入一个真子群的小循环。互质保证了遍历性

定理:循环群的任意一个子群也是循环群
推论1 设orda=n\text{ord}\,a = norda=n,rrr是任一整数。如果(n,r)=d(n, r) = d(n,r)=d,则 (ar)=⟨ad⟩(a^r) = \langle a^d \rangle(ar)=⟨ad⟩
推论2 设G=⟨a⟩G = \langle a \rangleG=⟨a⟩为循环群
- 如果∣G∣=∞|G| = \infty∣G∣=∞,则GGG的全部子群为 {⟨ad⟩∣d=0,1,2,…}\{\langle a^d \rangle \mid d = 0, 1, 2, \dots\}{⟨ad⟩∣d=0,1,2,…};
- 如果∣G∣=n|G| = n∣G∣=n,则GGG的全部子群为 {⟨ad⟩∣d\{\langle a^d \rangle \mid d{⟨ad⟩∣d为nnn的正因子}\}}。
定理:循环群的结构定理
设GGG为循环群
(1) 如果G=⟨a⟩G = \langle a \rangleG=⟨a⟩是无限循环群,则G≅(Z,+)G \cong (\mathbb{Z}, +)G≅(Z,+);
(2) 如果G=⟨a⟩G = \langle a \rangleG=⟨a⟩是nnn阶循环群,则G≅(Zn,+)G \cong (\mathbb{Z}_n, +)G≅(Zn,+)。
1.6置换群和对称群
定义:对称群与置换群
非空集合XXX的全体可逆变换(从集合XXX到集合XXX的双射变换)关于映射的合成构成集合XXX的对称群SXS_XSX,并且把SXS_XSX的任一子群叫做XXX的一个变换群。如果XXX是由nnn个元素组成的有限集合,则通常把XXX的一个可逆变换(从集合XXX到集合XXX的双射变换)叫做一个nnn阶置换(permutation),称SXS_XSX为nnn次对称群(symmetric group of degree nnn),并把SXS_XSX记作SnS_nSn,同时称SnS_nSn的子群为置换群(permutation group)。
理解:定义在非空集合XXX上的全体双射变换(双射变换的复合还是双射变换,见下图解)自然构成一个群,这个群我们叫做对称群SXS_XSX或者nnn次对称群(nnn为集合XXX元素的数量)记作SnS_nSn。SnS_nSn的任意一个子群都叫做置换群。

定理:有限群的凯莱定理
任何一个有限群同构于一个置换群。
定理:n次对称群SnS_nSn的阶是n!n!n!
例子:∣S1∣=1!=1|S_1| = 1! = 1∣S1∣=1!=1;X={1}X = \{1\}X={1};(11)\begin{pmatrix} 1 \\ 1 \end{pmatrix}(11)
∣S2∣=2!=2|S_2| = 2! = 2∣S2∣=2!=2;X={1,2}X = \{1,2\}X={1,2};(1212)\begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix}(1122),(1221)\begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix}(1221)
∣S3∣=3!=6|S_3| = 3! = 6∣S3∣=3!=6;X={1,2,3}X = \{1,2,3\}X={1,2,3};(123123)\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}(112233),(123132)\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}(112332),(123213)\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}(122133),(123231)\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}(122331),(123312)\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}(132132),(123321)\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}(132231)
定义:r轮换
设σ\sigmaσ是一个nnn阶置换. 如果存在111到nnn中的rrr个不同的数i1,i2,⋯,iri_1,i_2,\cdots,i_ri1,i2,⋯,ir,使
σ(i1)=i2\sigma(i_1)=i_2σ(i1)=i2, σ(i2)=i3\sigma(i_2)=i_3σ(i2)=i3, ⋯\cdots⋯, σ(ir−1)=ir\sigma(i_{r-1})=i_rσ(ir−1)=ir, σ(ir)=i1\sigma(i_r)=i_1σ(ir)=i1,
并且**σ\sigmaσ保持其余的元素不变**,则称σ\sigmaσ是一个长度为rrr的轮换(cycle),简称rrr轮换,记作 σ=(i1i2…ir)\sigma=(i_1\ i_2\ \dots\ i_r)σ=(i1 i2 … ir). 222轮换称为对换(transposition).
理解:轮换的表示一般不是唯一的。对于置换 σ=(12345672436517)\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 4 & 3 & 6 & 5 & 1 & 7 \end{pmatrix}σ=(12243346556177) 可分别表示为 σ=(1246)\sigma = (1\ 2\ 4\ 6)σ=(1 2 4 6) =(2461)= (2\ 4\ 6\ 1)=(2 4 6 1) =(4612)= (4\ 6\ 1\ 2)=(4 6 1 2) =(6124)= (6\ 1\ 2\ 4)=(6 1 2 4).
也可以用下面的图理解:

定义:不相交轮换
设σ=(i1i2…ir)\sigma=(i_1\ i_2\ \dots\ i_r)σ=(i1 i2 … ir)与τ=(j1j2…js)\tau=(j_1\ j_2\ \dots\ j_s)τ=(j1 j2 … js)是两个轮换,如果 ik≠jl,k=1,2,⋯,r;l=1,2,⋯,s,i_k \neq j_l, \ \ k = 1,2,\cdots,r; \ l = 1,2,\cdots,s,ik=jl, k=1,2,⋯,r; l=1,2,⋯,s, 则称σ\sigmaσ与τ\tauτ为两个不相交的轮换。
定理:任何两个不相交轮换的乘积是可以交换的.
定理:每一个置换可表位一些不相交轮换的乘积
例子:
将σ=(123456436152)\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 4 & 3 & 6 & 1 & 5 & 2 \end{pmatrix}σ=(142336415562)表为不相交轮换的乘积.
容易看出,σ\sigmaσ以下列顺序作用于XXX的元素: 1⟼4⟼1,1 \longmapsto 4 \longmapsto 1,1⟼4⟼1, 2⟼3⟼6⟼2,2 \longmapsto 3 \longmapsto 6 \longmapsto 2,2⟼3⟼6⟼2, 5⟼5.5 \longmapsto 5.5⟼5.
故 (123456436152)=(14)(236)(5)=(14)(236).\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 4 & 3 & 6 & 1 & 5 & 2 \end{pmatrix} = (14)(236)(5) = (14)(236).(142336415562)=(14)(236)(5)=(14)(236).
例子:
将下列轮换的乘积表示为不相交轮换的乘积: (3654)(3241)(3152).(3\ 6\ 5\ 4)(3\ 2\ 4\ 1)(3\ 1\ 5\ 2).(3 6 5 4)(3 2 4 1)(3 1 5 2).
解 设σ=(3654)\sigma = (3\ 6\ 5\ 4)σ=(3 6 5 4),δ=(3241)\delta = (3\ 2\ 4\ 1)δ=(3 2 4 1),η=(3152)\eta = (3\ 1\ 5\ 2)η=(3 1 5 2),则有 σδη:1⟼η5⟼δ5⟼σ44⟼η3⟼δ2⟼σ22⟼η4⟼δ1⟼σ13⟼η1⟼δ3⟼σ66⟼η6⟼δ6⟼σ55⟼η2⟼δ4⟼σ3\sigma\delta\eta: \begin{align*} 1 &\stackrel{\eta}{\longmapsto} 5 \stackrel{\delta}{\longmapsto} 5 \stackrel{\sigma}{\longmapsto} 4 \\ 4 &\stackrel{\eta}{\longmapsto} 3 \stackrel{\delta}{\longmapsto} 2 \stackrel{\sigma}{\longmapsto} 2 \\ 2 &\stackrel{\eta}{\longmapsto} 4 \stackrel{\delta}{\longmapsto} 1 \stackrel{\sigma}{\longmapsto} 1 \\ 3 &\stackrel{\eta}{\longmapsto} 1 \stackrel{\delta}{\longmapsto} 3 \stackrel{\sigma}{\longmapsto} 6 \\ 6 &\stackrel{\eta}{\longmapsto} 6 \stackrel{\delta}{\longmapsto} 6 \stackrel{\sigma}{\longmapsto} 5 \\ 5 &\stackrel{\eta}{\longmapsto} 2 \stackrel{\delta}{\longmapsto} 4 \stackrel{\sigma}{\longmapsto} 3 \\ \end{align*} σδη:142365⟼η5⟼δ5⟼σ4⟼η3⟼δ2⟼σ2⟼η4⟼δ1⟼σ1⟼η1⟼δ3⟼σ6⟼η6⟼δ6⟼σ5⟼η2⟼δ4⟼σ3 由此得 (3654)(3241)(3152)=(142)(365).(3\ 6\ 5\ 4)(3\ 2\ 4\ 1)(3\ 1\ 5\ 2) = (1\ 4\ 2)(3\ 6\ 5).(3 6 5 4)(3 2 4 1)(3 1 5 2)=(1 4 2)(3 6 5). 注意,计算的顺序应是从右到左。
定理:轮换的阶
如果σ\sigmaσ是一个rrr轮换,则ord σ=r\text{ord}\ \sigma = rord σ=r。
如果σ\sigmaσ是一些不相交轮换的乘积 σ=σ1σ2⋯σs,\sigma = \sigma_1 \sigma_2 \cdots \sigma_s,σ=σ1σ2⋯σs, 其中σi\sigma_iσi是rir_iri轮换,则ord σ=[r1,r2,⋯,rs]\text{ord}\ \sigma = [r_1, r_2, \cdots, r_s]ord σ=[r1,r2,⋯,rs]。
定理:置换转化为对换的奇偶不变性
将一个置换表为对换的乘积,所用对换个数的奇偶性是唯一的。
定义:奇置换和偶置换
可表成偶数个对换的乘积的置换叫偶置换(even permutation),可表成奇数个对换的乘积的置换叫奇置换(odd permutation)。
由定义易得:
(1) 任何两个偶(奇)置换之积是偶置换;
(2) 一个偶置换与一个奇置换之积是奇置换;
(3) 一个偶(奇)置换的逆置换仍是一个偶(奇)置换。
定理:SnS_nSn中奇置换和偶置换个数
当n>1n > 1n>1时,在全体nnn阶置换中,奇置换与偶置换各有n!2\frac{n!}{2}2n!个.
定理:n次交代群(交错群)
在SnS_nSn中,全体偶置换构成SnS_nSn的子群称为n次交代群(交错群),记作AnA_nAn.
*1.7置换在对称变换群中的应用
定义:对称变换群
使图形不变形地变到与自身重合的变换称为这个图形的对称变换(symmetric transformation). 一个图形的一切对称变换关于变换的乘法构成群, 这个群称为这个图形的对称变换群.
例:正方形的对称变换群
由图1.7.1不难看出,正方形的对称变换只有两种:
(1) 分别绕中心点OOO按逆时针方向旋转90∘90^\circ90∘,180∘180^\circ180∘,270∘270^\circ270∘,360∘360^\circ360∘的旋转;
(2) 关于直线L1L_1L1,L2L_2L2,L3L_3L3,L4L_4L4的镜面反射。
为了用置换来表示正方形的对称变换,用数字111,222,333,444来代表正方形的四个顶点(图1.7.1)。显然,正方形的每一个对称变换都导致了这四个顶点的一个置换。如果对称变换将顶点iii变为顶点kik_iki,那么用置换
(1234k1k2k3k4)\begin{pmatrix} 1&2&3&4 \\ k_1&k_2&k_3&k_4 \end{pmatrix}(1k12k23k34k4)
来表示这个对称变换。
表1.7.1 正方形的对称变换及其置换表示
| 对称变换 | 置换表示 |
|---|---|
| ccc表示绕中心旋转90∘90^\circ90∘ | (1234)(1\ 2\ 3\ 4)(1 2 3 4) |
| c2c^2c2表示绕中心旋转180∘180^\circ180∘ | (13)(24)(1\ 3)(2\ 4)(1 3)(2 4) |
| c3c^3c3表示绕中心旋转270∘270^\circ270∘ | (1432)(1\ 4\ 3\ 2)(1 4 3 2) |
| c4c^4c4表示绕中心旋转360∘360^\circ360∘(恒等变换) | (1)(1)(1) |
| v1v_1v1表示关于L1L_1L1的反射 | (12)(34)(1\ 2)(3\ 4)(1 2)(3 4) |
| v2v_2v2表示关于L2L_2L2的反射 | (14)(23)(1\ 4)(2\ 3)(1 4)(2 3) |
| v3v_3v3表示关于L3L_3L3的反射 | (24)(2\ 4)(2 4) |
| v4v_4v4表示关于L4L_4L4的反射 | (13)(1\ 3)(1 3) |
由表1.7.1可知,两个对称变换的乘积对应于相应的置换的乘积。所以正方形的对称变换群是S4S_4S4的一个子群,记作D4D_4D4。由表1.7.1可知∣D4∣=8|D_4|=8∣D4∣=8。
一般地,正nnn边形(n⩾3n \geqslant 3n⩾3)的对称变换群是SnS_nSn的一个子群,记作DnD_nDn,称为二面体群。易知,正nnn边形有nnn个旋转(包括恒等变换)和nnn个反射,所以,二面体群的阶数是2n2n2n。
第二章:群的进阶
2.1子群的陪集
定义:子群的乘积
设AAA与BBB是群GGG的两个非空子集,称集合 AB={ab∣a∈A,b∈B}AB = \{ab \mid a \in A, b \in B\}AB={ab∣a∈A,b∈B} 为群的子集AAA与BBB的乘积
定理:2.1.1
设A,B,CA,B,CA,B,C是群GGG的非空子集,ggg是群GGG的一个元素,则
(1) A(BC)=(AB)CA(BC) = (AB)CA(BC)=(AB)C;
(2) 如果gA=gBgA = gBgA=gB或Ag=BgAg = BgAg=Bg,则A=BA = BA=B;
(3) 如果HHH是群GGG的子群,则H⋅H=HH \cdot H = HH⋅H=H;
(4) 如果A,BA,BA,B是群GGG的两个子群,则ABABAB也是群GGG的子群的充分必要条件是AB=BAAB = BAAB=BA。
定义:左右陪集
设GGG是群,HHH是GGG的子群. 对任意的a∈Ga \in Ga∈G,群GGG的子集 aH={ah∣h∈H}与Ha={ha∣h∈H}aH = \{ah \mid h \in H\} \quad \text{与} \quad Ha = \{ha \mid h \in H\}aH={ah∣h∈H}与Ha={ha∣h∈H} 分别称为HHH在GGG中的左陪集 (left coset) 和右陪集 (right coset).
定理: 2.1.2
设HHH是群GGG的子群,a,b∈Ga,b \in Ga,b∈G,则
(1) a∈aHa \in aHa∈aH;
(2) aH=HaH = HaH=H的充分必要条件是a∈Ha \in Ha∈H;
(3) aHaHaH为子群的充分必要条件是a∈Ha \in Ha∈H;
(4) aH=bHaH = bHaH=bH的充分必要条件是a−1b∈Ha^{-1}b \in Ha−1b∈H;
(5) aHaHaH与bHbHbH或者完全相同,或者无公共元素;
(6) ∣aH∣=∣bH∣|aH| = |bH|∣aH∣=∣bH∣。
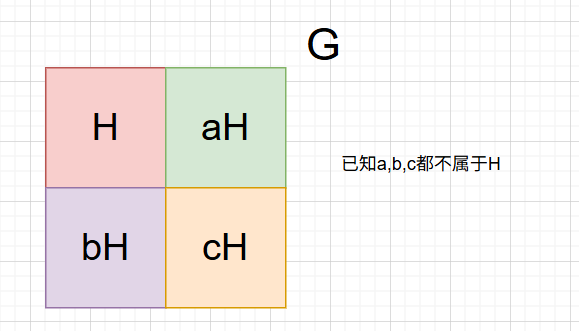
并且仅有H是群
定理:2.1.3
设HHH是群GGG的子群,用SLS_LSL表示HHH在GGG中的全体左陪集(即SL={gH∣g∈G}S_L = \{ gH \mid g \in G \}SL={gH∣g∈G},其中gHgHgH是左陪集),用SRS_RSR表示HHH在GGG中的全体右陪集(即SR={Hg∣g∈G}S_R = \{ Hg \mid g \in G \}SR={Hg∣g∈G},其中HgHgHg是右陪集)则∣SL∣=∣SR∣|S_L| = |S_R|∣SL∣=∣SR∣。
理解:子群HHH通过"左乘群GGG中元素"得到的所有左陪集,和通过"右乘群GGG中元素"得到的所有右陪集,数量是一样的。
定义:子群的指数
设GGG是群,HHH是GGG的子群. 称子群HHH在群GGG中的左陪集或右陪集的个数 (有限或无限) 为HHH在GGG中的指数 (index),记作[G:H][G:H][G:H].
定理:拉格朗日定理
设GGG是一个有限群,HHH是GGG的子群,则 ∣G∣=∣H∣[G:H].|G| = |H|[G:H].∣G∣=∣H∣[G:H]. 拉格朗日定理说明,有限群GGG的子群HHH的阶数与它在GGG中的指数,都是群GGG的阶数的因子。
理解:拉格朗日定理说明,有限群GGG的子群HHH的阶数与它在GGG中的指数,都是群GGG的阶数的因子.
推论 1 :设GGG是有限群,则GGG中每一个元素的阶都是∣G∣|G|∣G∣的因子.
理解:因为 aaa 的阶就是 ⟨a⟩\langle a \rangle⟨a⟩ 的阶,而 ⟨a⟩\langle a \rangle⟨a⟩ 的阶是 ∣G∣|G|∣G∣ 的因子,所以 aaa 的阶是 ∣G∣|G|∣G∣ 的因子. □
推论 2 :设GGG为有限群,∣G∣=n|G|=n∣G∣=n,则对任意的a∈Ga \in Ga∈G,有an=ea^n = ean=e.
注:将推论2应用到模ppp单位群Zp∗\boldsymbol{Z}_p^*Zp∗(ppp是素数),可以得到初等数论中著名的定理:
定理 2.1.5(费马 (Fermat) 小定理) 设ppp为素数,则对任意一个与ppp互素的整数aaa,有
ap−1≡1(modp).a^{p-1} \equiv 1 \pmod{p}.ap−1≡1(modp).
2.2正规子群与商群
定义:正规子群
设HHH是群GGG的子群,如果对每个a∈Ga \in Ga∈G,都有aH=HaaH = HaaH=Ha,则称HHH是群GGG的一个正规子群(normal subgroup)或不变子群(invariant subgroup),记作H◃GH \triangleleft GH◃G。
定理:2.2.1
设GGG是群,HHH是GGG的子群,则下列四个条件等价:
(1) HHH是GGG的正规子群;
(2) 对任意的a∈Ga \in Ga∈G,有aHa−1=HaHa^{-1} = HaHa−1=H;
(3) 对任意的a∈Ga \in Ga∈G,有aHa−1⊆HaHa^{-1} \subseteq HaHa−1⊆H;
(4) 对任意的a∈Ga \in Ga∈G,h∈Hh \in Hh∈H,有aha−1∈Haha^{-1} \in Haha−1∈H。
定理:2.2.2
交换群的任意子群都是正规子群,而循环群一定是交换群所以循环群的任意子群也一定是正规子群
定理:2.2.3
设GGG为群,H1,H2H_1, H_2H1,H2是GGG的正规子群,则H1∩H2H_1 \cap H_2H1∩H2与H1H2H_1H_2H1H2都是GGG的正规子群。
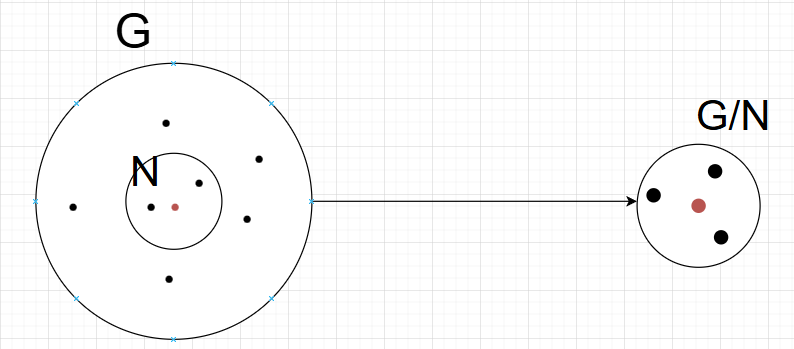
定义:商群
设GGG是群,HHH是GGG的一个正规子群,则HHH的所有陪集组成的集合 G/H={aH∣a∈G}G/H = \{aH \mid a \in G\}G/H={aH∣a∈G} 关于陪集的乘法aH⋅bH=(ab)HaH \cdot bH = (ab)HaH⋅bH=(ab)H构成群,称为群GGG关于子群HHH的商群(quotient group),仍记作G/HG/HG/H.
推论1:
设GGG为群,HHH是GGG的正规子群,则
(1) 商群G/HG/HG/H的单位元是eH(=H)eH(=H)eH(=H);
(2) aHaHaH在G/HG/HG/H中的逆元是a−1Ha^{-1}Ha−1H。
推论2:
设GGG为群,HHH是GGG的任一子群。如果GGG是交换群,则商群G/HG/HG/H也是交换群。
推论3:
有限群GGG的商群的阶是群GGG的阶数的因子。
研究商群的意义:
商群是一类极为重要的群,它从一开始就受到数学家们的特别关注。这是因为,商群是由其正规子群的陪集所构成,所以它在许多方面有与原来的群相似的性质(如果子群H≠GH \neq GH=G);同时,商群的结构又比原来的群简单一些(只要子群H≠{e}H \neq \{e\}H={e})。讨论商群的性质相对来说要比讨论原来的群的性质容易。这样,借助于商群,我们就可以部分地了解原来群的性质。从这一点来看,商群在理论上和实践上的意义当然是不言而喻的了。作为正规子群的应用。
理解:考虑一个G群,它可以被可视化为一个较大圆圈内的一组点。在这个圆圈内,有代表子群的小圆圈。 现在,想象N是这个表示中的一个特殊子群。商群G/N可以被视作将每个陪集的所有元素折叠成一个点。这创造出一个简化的结构,它仍然反映出群的性质。
举例:
设GGG为有限交换群,∣G∣=n|G|=n∣G∣=n。证明:对nnn的任一素因子ppp,GGG必有阶为ppp的元素。
证明: 对nnn应用数学归纳法。
首先,当n=2n=2n=2时,结论显然成立。
假设结论对所有阶小于nnn的交换群成立。考察阶为nnn的交换群GGG,设ppp为nnn的任一素因子。
任取a∈Ga \in Ga∈G,a≠ea \neq ea=e,设orda=r\text{ord}\,a = rorda=r。
(1) 如果r=pkr = pkr=pk,则ordak=p\text{ord}\,a^k = pordak=p,结论成立。
(2) 如果p∤rp \nmid rp∤r,令H=⟨a⟩H = \langle a \rangleH=⟨a⟩,则HHH为GGG的正规子群(见例3),且商群G/HG/HG/H为交换群(推论2)。而∣G/H∣=nr<n|G/H| = \frac{n}{r} < n∣G/H∣=rn<n,且因p∤rp \nmid rp∤r,所以p∣(nr)p \mid \left( \frac{n}{r} \right)p∣(rn)。从而由归纳假设知,存在bH∈G/HbH \in G/HbH∈G/H,使ordbH=p\text{ord}\,bH = pordbH=p,则bp∈Hb^p \in Hbp∈H。于是bpr=eb^{pr} = ebpr=e。由于p∤rp \nmid rp∤r,所以(bH)r≠H(bH)^r \neq H(bH)r=H,即br∉Hb^r \notin Hbr∈/H,于是br≠eb^r \neq ebr=e。而(br)p=e(b^r)^p = e(br)p=e,所以ordbr=p\text{ord}\,b^r = pordbr=p。
从而由归纳法原理知结论成立。
2.3群的同态和同构基本定理
引言:
1.3 节曾经说过,研究一件事物通常有三种方法,其中之一就是从一件事物与另一件事物的联系中去了解事物。在数学上,数学对象之间的联系往往是通过某种特殊的映射来反映的。这些映射不但建立了两个数学对象的元素之间的联系,而且也要能反映出这两个数学对象之间的某种结构上的联系。比如,线性代数中的线性映射就具有这一特点,它既建立了两个线性空间的元素之间的对应关系,同时也保持了双方的某些运算性质。在 1.4 节中所讨论过的群同构的概念也具有这一特性。但是,群同构的概念对于讨论群与群之间的关系来说条件太强了,它首先要求群与群的元素之间有一个一一对应的关系。在群论中,在讨论群与群之间的联系时,一个应用得更为广泛的概念是群同态的概念。与同构一样,群同态保持了群双方的运算,但却不要求群的元素之间是一一对应的。因此可以说,群同态是群同构的概念的自然推广。通过群同态,可以了解一个群与它的商群以及它的同态象之间的密切的联系。而这种联系,无论对于群论本身,还是对于群的应用,都是极为重要的。本节首先给出群同态的定义,然后讨论群同态的一些最基本的性质,最后证明群同态的基本定理。
定义:同态
设(G,⋅)(G,\cdot)(G,⋅)与(G′,∗)(G',*)(G′,∗)是两个群,ϕ\phiϕ是GGG到G′G'G′的映射。如果对任意的a,b∈Ga,b \in Ga,b∈G有 ϕ(a⋅b)=ϕ(a)∗ϕ(b),(2.3.1)\phi(a\cdot b) = \phi(a)*\phi(b), \tag{2.3.1}ϕ(a⋅b)=ϕ(a)∗ϕ(b),(2.3.1) 则称ϕ\phiϕ是群GGG到G′G'G′的一个同态映射(homomorphism),简称同态。
当同态映射ϕ\phiϕ是满射时,称ϕ\phiϕ为群GGG到G′G'G′的满同态(epimorphism),并称群GGG与G′G'G′同态,记作ϕ:G∼G′\phi: G \sim G'ϕ:G∼G′(或G∼ϕG′G \stackrel{\phi}{\sim} G'G∼ϕG′)。
当同态映射ϕ\phiϕ是单射时,称ϕ\phiϕ为GGG到G′G'G′的单同态(monomorphism)。
既是单射又是满射的同态是同构
定义: 自然同态
设 GGG 是一个群,HHH 是 GGG 的一个正规子群(即 N◃GN \triangleleft GN◃G)。定义映射 ϕ:G→G/H\phi: G \to G/Hϕ:G→G/H,对于任意 g∈Gg \in Gg∈G,令 ϕ(g)=gH\phi(g) = gHϕ(g)=gH。这里 gHgHgH 是 ggg 所在的陪集,也就是商群 G/HG/HG/H 中的一个元素。 这个映射 ϕ\phiϕ 称为从群 GGG 到商群 G/HG/HG/H 的自然同态(或典范同态)。
定理:2.3.1同态下元素的关系
设ϕ\phiϕ是群GGG到群G′G'G′的同态映射,eee与e′e'e′分别是GGG与G′G'G′的单位元,a∈Ga \in Ga∈G,则
(1) ϕ\phiϕ将GGG的单位元映到G′G'G′的单位元,即ϕ(e)=e′\phi(e) = e'ϕ(e)=e′;
(2) ϕ\phiϕ将aaa的逆元映到ϕ(a)\phi(a)ϕ(a)的逆元,即ϕ(a−1)=(ϕ(a))−1\phi(a^{-1}) = (\phi(a))^{-1}ϕ(a−1)=(ϕ(a))−1;
(3) 设nnn是任一整数,则ϕ(an)=(ϕ(a))n\phi(a^n) = (\phi(a))^nϕ(an)=(ϕ(a))n;
(4) 如果orda\text{ord}\,aorda有限,则ordϕ(a)∣orda\text{ord}\,\phi(a) \mid \text{ord}\,aordϕ(a)∣orda。
定理:2.3.2同态下子群的关系
设ϕ\phiϕ是群GGG到G′G'G′的同态映射,HHH与KKK分别是GGG与G′G'G′的子群,则
(1) ϕ(H)\phi(H)ϕ(H)是G′G'G′的子群;
(2) ϕ−1(K)\phi^{-1}(K)ϕ−1(K)是GGG的子群;
(3) 如果HHH是GGG的正规子群,则ϕ(H)\phi(H)ϕ(H)是ϕ(G)\phi(G)ϕ(G)的正规子群;
(4) 如果KKK是G′G'G′的正规子群,则ϕ−1(K)\phi^{-1}(K)ϕ−1(K)是GGG的正规子群。
定义:核
设ϕ\phiϕ是群GGG到G′G'G′的同态映射,e′e'e′是G′G'G′的单位元,则称e′e'e′在GGG中的原象
ϕ−1({e′})={a∈G∣ϕ(a)=e′}\phi^{-1}(\{e'\}) = \{a \in G \mid \phi(a) = e'\}ϕ−1({e′})={a∈G∣ϕ(a)=e′}
为同态映射ϕ\phiϕ的核(kernel),记作Kerϕ\text{Ker}\,\phiKerϕ.
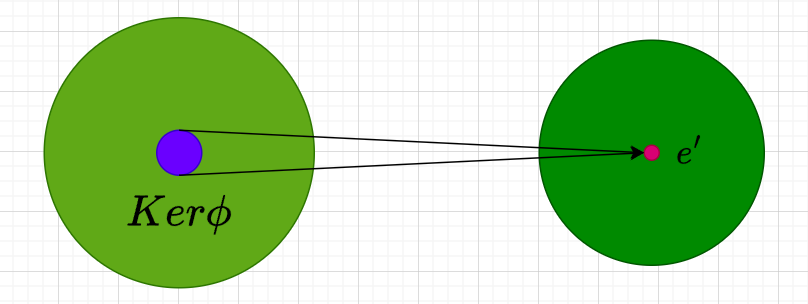
定理:2.3.3
设ϕ\phiϕ是群GGG到G′G'G′的同态映射,则Kerϕ\text{Ker}\,\phiKerϕ是GGG的正规子群。
定理:2.3.4(群同态基本定理)
设ϕ\phiϕ是群GGG到群G′G'G′的满同态,K=KerϕK = \text{Ker}\,\phiK=Kerϕ,则 G/K≅G′.G/K \cong G'.G/K≅G′.
理解:群同态基本定理是群论中一个十分重要而且经常用到的定理. 由这个定理可知, 从同构的观点来看, 群的同态象就是群的商群. 因此, 既可以由群的同态象去研究群的商群, 同时又可以借助于群的商群对群的同态象作系统的描述. 以下面的例子来说明群同态基本定理的某些应用.

2.4群的直积
2.5群在集合上作用
2.6西罗定理
参考:
近世代数 | 韩士安, 林磊 | download on Z-Library近世代数 ——韩士安
代数结构入门:群、环、域、向量空间 - 知乎
[【静夜思】一些抽象代数的核心思想和实际应用_抽象代数有什么用-CSDN博客](
