C语言用Cramer法则求解n元方程组
Cramer法则是求解n元一次线性方程组的重要手段。本程序利用Cramer法则的原理,实现方程组的求解。
数学原理
Cramer法则的内容是:
当系数矩阵A=(aij)n×n的行列式不等于零时,线性方程组
{a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯an1x1+an2x2+⋯+annxn=bn\left \{ \begin{array}{l} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2 \\ \cdots\\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \end{array} \right. ⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯an1x1+an2x2+⋯+annxn=bn
有唯一解
(x1,x2,⋯,xn)=(Δ1Δ,Δ2Δ,⋯,ΔnΔ)(x_1,x_2,\cdots,x_n)=(\frac{\Delta_1}{\Delta},\frac{\Delta_2}{\Delta},\cdots,\frac{\Delta_n}{\Delta}) (x1,x2,⋯,xn)=(ΔΔ1,ΔΔ2,⋯,ΔΔn)
其中Δ=det(A),Δi是将A的第i列换成常数项后所得方阵的行列式,i=1,2,…,n。
完整代码
#include <stdio.h>
#include "solve_det.h"int main() {int n;printf("n = ");scanf("%d", &n);int coef[n*n];int cons[n];for (int eqt = 0; eqt < n; eqt++) {printf("the conefficients and constant of equation %d: ", eqt + 1);for (int c = 0; c < n; c++) {scanf("%d", &coef[eqt*n+c]);}scanf("%d", &cons[eqt]);}int DET = solve_det(coef, n);if (DET == 0) {printf("The determinant of the coefficient matrix is 0!");return 0;}else {int DETs[n][n*n];double Xs[n];for (int i = 0; i < n; i++) {for (int j = 0; j < n * n; j++) {DETs[i][j] = coef[j];}for (int j = 0; j < n; j++) {DETs[i][j*n+i] = cons[j];}Xs[i] = 1.0 * solve_det(DETs[i], n) / DET;}for (int i = 0; i < n; i++) {printf("x_%d = %.2f\n", i + 1, Xs[i]);}return 0;}
}
其中头文件solve_det.h的代码如下:
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}int odd_even(int list[], int size) {int o_e = 1;for (int i = 0; i < size; i++) {for (int j = i + 1; j < size; j++) {if (list[i] > list[j]) {o_e = -o_e;}}}return o_e;
}int last(int list[], int size) {for (int i = 0; i < size; i++) {if (list[i] != size - i - 1) {return 0;}}return 1;
}void sort(int list[], int size, int first) {int smallest, smallestx;for (int i = first; i < size - 1; i++) {smallest = size;for (int j = i; j < size; j++) {if (list[j] < smallest) {smallest = list[j];smallestx = j;}}swap(&list[i], &list[smallestx]);}
}void next(int list[], int size) {int bigger, biggerx, first;for (int i = size - 2; i >= 0; i--) {first = list[i];bigger = size + 1;for (int j = i + 1; j < size; j++) {if (list[j] > first && list[j] < bigger) {bigger = list[j];biggerx = j;}}if (bigger < size + 1) {swap(&list[i], &list[biggerx]);sort(list, size, i + 1);return;}}
}int solve_det(int det[], int n) {int nums[n];for (int i = 0; i < n; i++) {nums[i] = i;}int result = 0, r;while (1) {r = odd_even(nums, n);for (int k = 0; k < n; k++) {r *= det[k*n+nums[k]];}result += r;if (last(nums, n)) {return result;}else {next(nums, n);}}
}
代码解释
关于solve_det.h的解释见《C语言计算矩阵的逆》的代码解释部分,主要包含计算行列式的值的函数。下面对本程序的代码进行逐段解释。
输入所有系数和常数
int n;
printf("n = ");
scanf("%d", &n);int coef[n*n];
int cons[n];
for (int eqt = 0; eqt < n; eqt++) {printf("the conefficients and constant of equation %d: ", eqt + 1);for (int c = 0; c < n; c++) {scanf("%d", &coef[eqt*n+c]);}scanf("%d", &cons[eqt]);
}
n是方程的个数,同时等于未知数的个数。Cramer法则的适用条件是方程个数等于未知数个数,此时方程组有且仅有一组解。所有系数按顺序存储在coef数组中,常数存储在cons数组中。
判断系数矩阵行列式是否为零
int DET = solve_det(coef, n);
if (DET == 0) {printf("The determinant of the coefficient matrix is 0!");return 0;
}
利用solve_det.h中的solve_det函数,得到系数矩阵行列式的值DET。若DET=0,则提示用户并中止运行。否则继续执行后续步骤:
计算方程组的解
else {int DETs[n][n*n];double Xs[n];for (int i = 0; i < n; i++) {for (int j = 0; j < n * n; j++) {DETs[i][j] = coef[j];}for (int j = 0; j < n; j++) {DETs[i][j*n+i] = cons[j];}Xs[i] = 1.0 * solve_det(DETs[i], n) / DET;}for (int i = 0; i < n; i++) {printf("x_%d = %.2f\n", i + 1, Xs[i]);}return 0;
}
计算每个未知数的值,需要先将系数矩阵的对应列元素换成同一个方程中的对应常数,再计算新矩阵的行列式的值,再除以DET。因此,将未知数的类型设定为double,打印时设定保留小数点后两位。数组Xs存储的就是x1~xn的计算结果。
运行结果示例
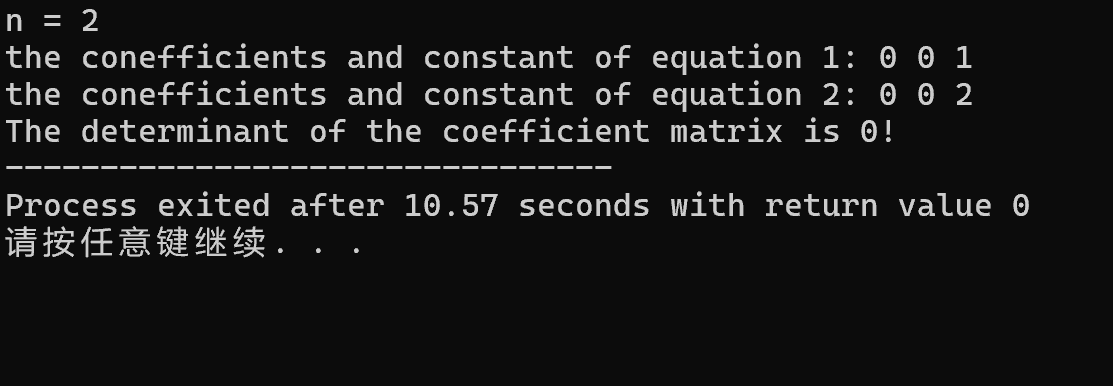
当系数矩阵的行列式的值为零时,程序中止:
以下是一个正确的计算结果: