【计算机视觉】霍夫变换检测

目录

一、引言

二、霍夫检测直线

（一）霍夫检测直线的思想

（二）实际应用

1.HoughLinesP()函数

2.HoughLines()函数

3. HoughLinesP与HoughLines的对比

三、霍夫检测圆

四、本文用到的图片样例

五、总结

---

一、引言

霍夫变换（Hough Transform）是图像处理中的一种特征提取技术，它通过一种投票算法检测具有特定形状的物体。该过程在一个参数空间中通过计算累计结果的局部最大值，得到一个符合该特定形状的集合作为霍夫变换结果。

霍夫变换于 1962 年由 Paul Hough 首次提出，后于 1972 年由 Richard Duda 和 Peter Hart 推广使用。经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别（多为圆和椭圆）。

霍夫变换运用两个坐标空间之间的变换，将 “一个空间中具有相同形状的曲线或直线” 映射到 “另一个坐标空间的一个点上” 形成峰值，从而把 “检测任意形状的问题” 转化为 “统计峰值问题”。

二、霍夫检测直线

对于平面中的一条直线，在笛卡儿坐标系中，常见的有点斜式、两点式两种表示方法。但在霍夫变换中，采用另一种表示方式：使用 (r, ) 来表示一条直线。其中，r 为该直线到原点的距离， 为该直线的垂线与 x 轴的夹角。

（一）霍夫检测直线的思想

使用霍夫变换检测直线的思想是：为每一个点假设 n 个方向的直线（通常 n=180，此时直线的角度精度为 ），分别计算这 n 条直线的 (r,θ) 坐标，得到 n 个坐标点。

若要判断的点共有 N 个，最终会得到 N×n 个 (r,θ) 坐标（其中 θ 是离散角度，共 180 个取值）。

最重要的规律是：如果多个点在同一条直线上，那么这些点在 ​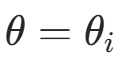 时，其 r 会近似等于 —— 即这些点都落在直线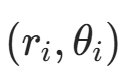上。

（二）实际应用

在实际的直线检测场景中，如果超过一定数目的点拥有相同的 (r,θ) 坐标，则可判定此处存在一条直线。在 r−θ 坐标系图中，“明显的交汇点” 就表示一条检测出的直线。

例如：用到Canny进行边缘检测，来提取车道线，代码如下：

import cv2
lane = cv2.imread("final_roi.png")
# 高斯模糊，Canny边缘检测需要的
lane = cv2.GaussianBlur(lane, (5, 5), 0)
# 进行边缘检测，减少图像空间中需要检测的点数量
lane = cv2.Canny(lane, 50, 150)
cv2.imshow("lane", lane)
cv2.imwrite('detected_lane_result.jpg', lane)
cv2.waitKey()

1.HoughLinesP()函数

cv2.HoughLinesP 是 OpenCV 中用于概率霍夫变换（Probabilistic Hough Transform）的函数，专门用于检测图像中的线段（有限长度的直线段），在计算机视觉的直线特征提取任务中（如车道线检测、工业轮廓识别等）应用广泛。

（1） 核心原理与优势

霍夫变换的本质是 **“图像空间→参数空间” 的转换 **：将图像中 “直线的检测” 转化为 “参数空间中投票峰值的寻找”。

• 传统霍夫变换（cv2.HoughLines）检测无限长的直线，返回直线的极坐标参数 (r,θ)。
• HoughLinesP 是概率霍夫变换，更高效且直接检测有限长度的线段，通过 “随机采样 + 投票” 减少计算量，还能直接返回线段的起点和终点坐标，更贴合实际应用场景（如自动驾驶中 “车道线是线段” 的需求）。

（2） 函数参数解析

函数形式：

lines = cv2.HoughLinesP(image, rho, theta, threshold, minLineLength=None, maxLineGap=None)

各参数含义：

• image：输入图像，必须是二值边缘图像（通常由 Canny、Sobel 等边缘检测得到，用于突出直线的边缘特征）。
• rho：距离分辨率（单位：像素），表示霍夫参数空间中 “直线到原点的距离 r” 的精度。值越小，检测精度越高，但计算量越大。
• theta：角度分辨率（单位：弧度），表示霍夫参数空间中 “直线垂线与 x 轴夹角 θ” 的精度。例如 np.pi/180 表示 1° 的精度。
• threshold：累加器阈值。只有当某条线段的 “投票数”（即有多少边缘点支持这条线段）≥ 该阈值时，才会被判定为 “有效线段”。阈值越高，检测的线段越 “可信”，但可能漏掉弱边缘的线段；阈值越低，检测的线段越多，但噪声也会增加。
• minLineLength：线段的最小长度。短于该长度的线段会被过滤，用于排除 “零碎的短线段”。
• maxLineGap：线段间的最大间隔。若两条线段的端点距离 ≤ 该值，会被合并为一条线段，用于连接 “接近但未完全连续” 的线段。

（3） 工作流程

HoughLinesP 的执行分为 4 个关键步骤：

1. 图像预处理：输入需为二值边缘图像（如 Canny 输出），目的是提取图像中的边缘特征，减少无效计算。
2. 概率霍夫投票：在霍夫参数空间（r−θ 空间）中，通过 “随机采样部分边缘点 + 投票统计” 的方式，快速寻找潜在的线段。
3. 阈值与长度 / 间隔过滤：先用 threshold 筛选 “投票数足够” 的线段，再通过 minLineLength 过滤短线、maxLineGap 合并接近的线段。
4. 输出线段坐标：返回所有检测到的线段，每个线段以 (x1, y1, x2, y2) 表示（起点和终点的像素坐标）。

（4） 参数调优与应用场景

参数需根据场景灵活调整：

• rho & theta：通常设为较小值（如 rho=1、theta=np.pi/180）保证基础精度；若对速度要求极高，可适当增大（但会降低精度）。
• threshold：噪声大时提高阈值（过滤噪声）；边缘弱时降低阈值（保留更多线段）。
• minLineLength & maxLineGap：检测长线段（如车道线）时，增大 minLineLength、减小 maxLineGap；检测短而零散的线段时，减小 minLineLength、增大 maxLineGap。

典型应用：

• 自动驾驶：检测车道线、交通标志的直线轮廓。
• 工业视觉：检测生产线上零件的边缘线段、缺陷的直线特征。
• 机器人导航：识别环境中的墙体、门框等直线型结构。

示例代码：

import numpy as np
import cv2lane = cv2.imread("lane.jpg")
# 高斯模糊，Canny边缘检测需要的
lane = cv2.GaussianBlur(lane, (5, 5), 0)
# 进行边缘检测，减少图像空间中需要检测的点数量
lane = cv2.Canny(lane, 50, 150)
cv2.imshow("lane", lane)
cv2.waitKey()rho = 1  # 距离分辨率
theta = np.pi / 180  # 角度分辨率
threshold = 10  # 霍夫空间中曲线相交的“有效交点”阈值
min_line_len = 10  # 构成一条直线的最少像素点数量
max_line_gap = 50  # 线段之间的最大间隔像素
lines = cv2.HoughLinesP(lane, rho, theta, threshold, maxLineGap=max_line_gap)line_img = np.zeros_like(lane)
for line in lines:for x1, y1, x2, y2 in line:cv2.line(line_img, (x1, y1), (x2, y2), 255, 1)cv2.imshow("line_img", line_img)
cv2.waitKey()

2.HoughLines()函数

HoughLines() 是计算机视觉中经典霍夫变换（Hough Transform）的核心函数，用于在图像中检测无限长的直线，广泛应用于车道线检测、工业缺陷检测等场景。

（1）核心功能

基于 “图像空间→极坐标参数空间” 的转换，通过 “投票统计” 检测图像中由边缘点构成的无限长直线，输出直线的极坐标参数（距离 ρ + 角度 θ）。

（2）参数与返回值（以 OpenCV 版本为例）

函数原型：

lines = cv2.HoughLines(image, rho, theta, threshold)

1. 输入参数

• image：输入图像，必须是 8 位灰度的二值图像（通常由 Canny 等边缘检测生成，突出直线的边缘特征）。
• rho：距离分辨率（单位：像素），表示 “直线到图像原点的距离 ρ” 的精度。值越小，检测越精细，但计算量越大。
• theta：角度分辨率（单位：弧度），表示 “直线垂线与 x 轴的夹角 θ” 的精度。例如 np.pi/180 表示 1° 精度。
• threshold：累加器阈值。只有 “投票数”（支持该直线的边缘点数量）≥ 此阈值的直线，才会被判定为有效。阈值越高，直线越 “可信” 但易漏检；阈值越低，检测直线越多但噪声大。
• 可选参数（如 srn、stn、min_theta、max_theta）：用于多尺度霍夫变换或限制角度范围，默认用经典霍夫变换时可忽略。

2. 返回值

返回数组 lines，每个元素为 (rho, theta) 元组，含义：

• ρ：直线到图像左上角原点 (0,0) 的垂直距离（单位：像素）。
• θ：直线的垂线与 x 轴的夹角（单位：弧度）。

（3）原理：“投票机制” 与空间转换

经典霍夫变换的核心是 “从图像空间到极坐标参数空间的映射”：

1. 图像空间的点 → 参数空间的曲线：图像中每个边缘点，在极坐标参数空间（ρ−θ 平面）对应一条正弦曲线（满足 ρ=xcosθ+ysinθ）。
2. 投票统计峰值：若多个边缘点共线，它们在参数空间的正弦曲线会交汇于同一点（即 “投票峰值”）。
3. 提取直线：当投票数超过 threshold 时，该交点对应的 (ρ,θ) 就是图像中存在的直线。

（4）特点与局限性

• 特点：
  • 检测无限长的直线，精度高（由 rho 和 theta 控制）。
  • 能检测 “部分被遮挡或有噪声” 的直线（只要边缘点足够多）。
• 局限性：
  • 计算量大（需遍历所有边缘点并映射到参数空间）。
  • 仅能输出 “无限长直线的极坐标”，无法直接得到线段的端点（若需线段检测，需用 HoughLinesP）。

示例代码：

import cv2
import numpy as np
import matplotlib.pyplot as pltimg = cv2.imread('line.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 转换为灰度图像
edges = cv2.Canny(gray, 50, 200)  # Canny边缘检测# 显示边缘检测结果
plt.subplot(121), plt.imshow(edges, 'gray')
plt.xticks([]), plt.yticks([])# HoughLines 霍夫直线变换
lines = cv2.HoughLines(edges, 1, np.pi/180, 160)
lines1 = lines[:, 0, :]  # 提取为二维数组# 遍历每条检测到的直线，绘制到原图
for rho, theta in lines1[:]:a = np.cos(theta)b = np.sin(theta)x0 = a * rhoy0 = b * rhox1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * (a))x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 * (a))cv2.line(img, (x1, y1), (x2, y2), (255, 0, 0), 1)# 显示绘制直线后的结果
plt.subplot(122), plt.imshow(img)
plt.xticks([]), plt.yticks([])
plt.show()

3. HoughLinesP与HoughLines的对比

HoughLinesP 是概率霍夫变换（对经典霍夫的优化），二者核心差异如下：

函数	霍夫变换类型	检测对象	计算效率	输出形式
HoughLines	经典霍夫	无限长直线	较低	极坐标 (ρ,θ)
HoughLinesP	概率霍夫	有限长线段	较高	线段端点 (x1,y1,x2,y2)

三、霍夫检测圆

圆形的表达式为(x−xcenter​)2+(y−ycenter​)2=r2，确定一个圆环需要 3 个参数。那么霍夫变换的累加器必须是三维的，但是这样的计算效率很低。

因此，OpenCV 中使用霍夫梯度的方法，这里利用了边界的梯度信息。首先对图像进行 Canny 边缘检测，对边缘中的每一个非 0，通过 Sobel 算法计算局部梯度。那么计算得到的梯度方向，实际上就是圆切线的法线。3 条法线即可确定一个圆心；同理，在累加器中对圆心通过的法线进行累加，就得到了圆环的判定。

以霍夫梯度法实现圆环检测的函数为：

cv2.HoughCircles(image, method, dp, minDist, circles, param1, param2, minRadius, maxRadius)

其中，各参数含义如下：

• image—— 输入图像，格式为灰度图；
• method—— 检测方法，常用CV_HOUGH_GRADIENT。
• dp—— 检测内侧圆心的累加器图像的分辨率与输入图像之比的倒数，如果dp=1，则累加器和输入图像具有相同的分辨率；如果dp=2，则累计器有输入图像一半那么大的宽度和高度。
• minDist—— 两个圆之间圆心的最小距离。
• param1—— 默认值为 100，它是method设置的检测方法的对应参数，对当前唯一的方法 —— 霍夫梯度法cv2.HOUGH_GRADIENT，它表示传递给 Canny 边缘检测算子的高阈值，而低阈值为高阈值的一半。
• param2—— 默认值为 100，它是method设置的检测方法的对应的参数，对当前唯一的方法 —— 霍夫梯度法cv2.HOUGH_GRADIENT，它表示在检测阶段圆心的累加器阈值。它越小，就越可以检测到更多根本不存在的圆；它越大，能通过检测的圆就更加接近完美的圆形。
• minRadius—— 默认值为 0，圆半径的最小值。
• maxRadius—— 默认值为 0，圆半径的最大值。

示例代码：

import cv2
import numpy as np# 1. 读取图像（确保文件名与实际一致）
img = cv2.imread('4.png', 0)  # 以灰度模式读取
if img is None:print("无法读取图像！请检查文件路径/名称是否正确。")exit()# 2. 预处理：中值滤波降噪
img = cv2.medianBlur(img, 5)
cimg = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)  # 转彩色（用于绘制彩色圆）# 3. 霍夫圆变换（调整参数以适配足球特征）
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,dp=1,  # 累加器分辨率与图像分辨率的比值minDist=30,  # 圆心间最小距离param1=80,  # Canny边缘检测的高阈值param2=25,  # 霍夫空间“圆心”的累加阈值minRadius=0,  # 圆的最小半径maxRadius=300  # 圆的最大半径
)# 4. 空值检查：确保检测到了圆
if circles is not None:circles = np.uint16(np.around(circles))  # 坐标转整数# 遍历检测到的圆，绘制外圆和圆心for i in circles[0, :]:# 画外圆（绿色，线宽2）cv2.circle(cimg, (i[0], i[1]), i[2], (0, 255, 0), 2)# 画圆心（红色，线宽3，小圆半径2）cv2.circle(cimg, (i[0], i[1]), 2, (0, 0, 255), 3)# 显示结果cv2.imshow('detected circles', cimg)# 保存结果图片save_success = cv2.imwrite('detected_circles_result.jpg', cimg)if save_success:print("检测结果已成功保存为 'detected_circles_result.jpg'")else:print("保存图片失败，请检查是否有写入权限或路径是否正确")cv2.waitKey(0)
else:print("未检测到圆！请调整霍夫圆变换的参数（如 param2、minDist 等）。")cv2.destroyAllWindows()

四、本文用到的图片样例

五、总结

本文介绍了霍夫变换（Hough Transform）在图像处理中的应用，重点阐述了直线和圆形的检测方法及其实现。首先概述了霍夫变换的基本原理，即通过参数空间转换将图像中的形状检测转化为统计峰值问题。随后详细讲解了两种直线检测方法：经典霍夫变换（HoughLines）检测无限长直线，返回极坐标参数；概率霍夫变换（HoughLinesP）更高效地检测有限线段，直接输出端点坐标。对于圆形检测，介绍了基于霍夫梯度法的实现（HoughCircles），并分析了各参数对检测结果的影响。文章还提供了完整的代码示例，展示了从图像预处理到形状检测的完整流程，包括参数调优建议和实际应用场景。最后通过对比不同方法的特点，帮助读者根据具体需求选择合适的检测方案。