单调队列与单调栈

单调队列和单调栈是两种基于单调性设计的数据结构，用于高效解决“区间极值”“最近更大/小元素”等问题，核心思想是维护队列/栈内元素的单调递增或递减性，从而将时间复杂度优化到线性。

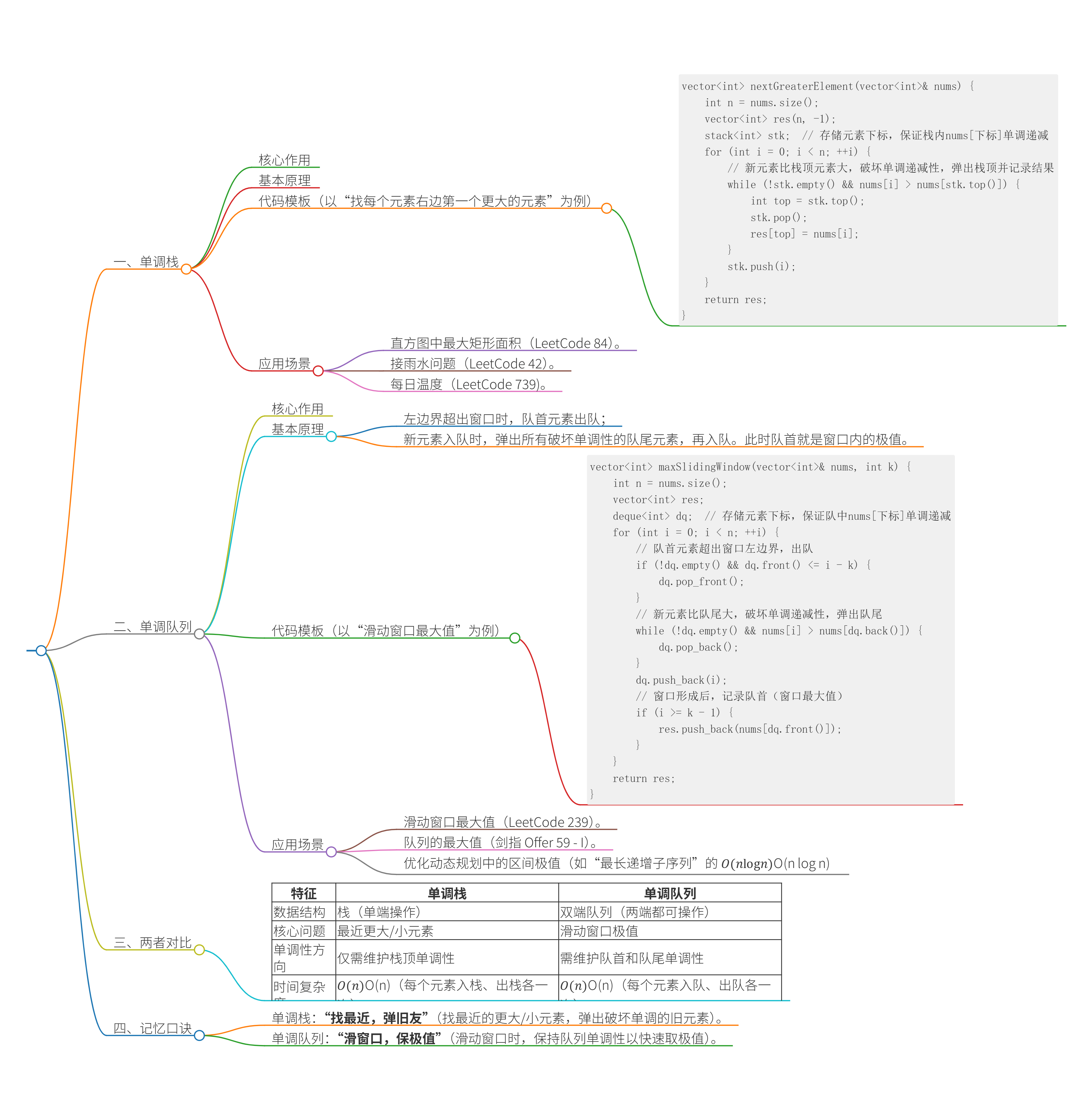
一、单调栈

核心作用

快速找到每个元素左边/右边第一个比它大（或小）的元素。

基本原理

维护一个栈，栈内元素单调递增或递减。当新元素入栈时，弹出所有破坏单调性的元素，再将新元素入栈。此时，栈顶（或被弹出元素的下一个元素）就是“最近的符合条件的元素”。

代码模板（以“找每个元素右边第一个更大的元素”为例）

vector<int> nextGreaterElement(vector<int>& nums) {int n = nums.size();vector<int> res(n, -1);stack<int> stk;  // 存储元素下标，保证栈内nums[下标]单调递减for (int i = 0; i < n; ++i) {// 新元素比栈顶元素大，破坏单调递减性，弹出栈顶并记录结果while (!stk.empty() && nums[i] > nums[stk.top()]) {int top = stk.top();stk.pop();res[top] = nums[i];}stk.push(i);}return res;
}

应用场景

• 直方图中最大矩形面积（LeetCode 84）。
• 接雨水问题（LeetCode 42）。
• 每日温度（LeetCode 739)。

二、单调队列

核心作用

在滑动窗口中快速找到窗口内的最大值或最小值。

基本原理

维护一个双端队列（deque），队列内元素单调递增或递减。窗口滑动时：

• 左边界超出窗口时，队首元素出队；
• 新元素入队时，弹出所有破坏单调性的队尾元素，再入队。此时队首就是窗口内的极值。

代码模板（以“滑动窗口最大值”为例）

vector<int> maxSlidingWindow(vector<int>& nums, int k) {int n = nums.size();vector<int> res;deque<int> dq;  // 存储元素下标，保证队中nums[下标]单调递减for (int i = 0; i < n; ++i) {// 队首元素超出窗口左边界，出队if (!dq.empty() && dq.front() <= i - k) {dq.pop_front();}// 新元素比队尾大，破坏单调递减性，弹出队尾while (!dq.empty() && nums[i] > nums[dq.back()]) {dq.pop_back();}dq.push_back(i);// 窗口形成后，记录队首（窗口最大值）if (i >= k - 1) {res.push_back(nums[dq.front()]);}}return res;
}

应用场景

• 滑动窗口最大值（LeetCode 239）。
• 队列的最大值（剑指 Offer 59 - I）。
• 优化动态规划中的区间极值（如“最长递增子序列”的 $O(n\log n)$ 优化）。

三、两者对比

特征	单调栈	单调队列
数据结构	栈（单端操作）	双端队列（两端都可操作）
核心问题	最近更大/小元素	滑动窗口极值
单调性方向	仅需维护栈顶单调性	需维护队首和队尾单调性
时间复杂度	$O(n)$（每个元素入栈、出栈各一次）	$O(n)$（每个元素入队、出队各一次）
典型应用	直方图、接雨水	滑动窗口最值、DP优化

四、记忆口诀

• 单调栈：“找最近，弹旧友”（找最近的更大/小元素，弹出破坏单调的旧元素）。
• 单调队列：“滑窗口，保极值”（滑动窗口时，保持队列单调性以快速取极值）。