C语言计算行列式的值

行列式是线性代数学科中的一项重要内容，而其求值却往往比较繁琐。本程序利用C语言，实现了对行列式的计算求值，极大地提高了运用行列式解题的速度和准确率。

数学原理

本程序依据的数学原理是行列式的完全展开式：
$$det(A)=\sum _{(j_1,j_2,\cdots ,j_n)\in S_n}(-1{)}^{\tau (j_1,j_2,\cdots ,j_n)}{a}_{1j_1}{a}_{2j_2}\cdots a_{n{j}_n}$$
其中，$$\tau (j_1,j_2,\cdots ,j_n)$$指的是该序列的逆序数。

完整代码

本程序完整代码如下：

#include <stdio.h>void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}int odd_even(int list[], int size) {int o_e = 1;for (int i = 0; i < size; i++) {for (int j = i + 1; j < size; j++) {if (list[i] > list[j]) {o_e = -o_e;}}}return o_e;
}int last(int list[], int size) {for (int i = 0; i < size; i++) {if (list[i] != size - i - 1) {return 0;}}return 1;
}void sort(int list[], int size, int first) {int smallest, smallestx;for (int i = first; i < size - 1; i++) {smallest = size;for (int j = i; j < size; j++) {if (list[j] < smallest) {smallest = list[j];smallestx = j;}}swap(&list[i], &list[smallestx]);}
}void next(int list[], int size) {int bigger, biggerx, first;for (int i = size - 2; i >= 0; i--) {first = list[i];bigger = size + 1;for (int j = i + 1; j < size; j++) {if (list[j] > first && list[j] < bigger) {bigger = list[j];biggerx = j;}}if (bigger < size + 1) {swap(&list[i], &list[biggerx]);sort(list, size, i + 1);return;}}
}int main() {int n;printf("n = ");scanf("%d", &n);int nums[n];for (int i = 0; i < n; i++) {nums[i] = i;}int det[n][n];for (int r = 0; r < n; r++) {printf("row %d: ", r + 1);for (int c = 0; c < n; c++) {scanf("%d", &det[r][c]);}}int result = 0, r;while (1) {r = odd_even(nums, n);for (int k = 0; k < n; k++) {r *= det[k][nums[k]];}result += r;if (last(nums, n)) {printf("%d", result);return 0;}else {next(nums, n);}}
}

代码解释

下面对本程序的代码逐段地进行拆解。

数组交换函数swap

void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}

该函数能将数组中两个元素互换位置，实际上是通过使其指针分别指向对方的值来实现的。

排列奇偶性确定函数odd_even

int odd_even(int list[], int size) {int o_e = 1;for (int i = 0; i < size; i++) {for (int j = i + 1; j < size; j++) {if (list[i] > list[j]) {o_e = -o_e;}}}return o_e;
}

该函数的返回值就是完全展开式中的系数：
$$(-1{)}^{\tau (j_1,j_2,\cdots ,j_n)}$$
由于真正的逆序数并不影响计算结果，真正起作用的只是逆序数的奇偶性，奇数时系数为-1，偶数时系数为1，因此该函数的返回值o_e就是1或-1，这也便于后续计算。

遍历结束判断函数last

int last(int list[], int size) {for (int i = 0; i < size; i++) {if (list[i] != size - i - 1) {return 0;}}return 1;
}

由于该函数需要将从1到n的序列$$j_1,j_2,\cdots ,j_n$$完整地遍历一遍，所以需要确定何时遍历终止。具体而言，就是当$$j_k=n-k-1$$时遍历终止，即序列完全反向了。

排序函数sort

void sort(int list[], int size, int first) {int smallest, smallestx;for (int i = first; i < size - 1; i++) {smallest = size;for (int j = i; j < size; j++) {if (list[j] < smallest) {smallest = list[j];smallestx = j;}}swap(&list[i], &list[smallestx]);}
}

程序运行的某些步骤中，需要用到将序列从某一项开始至最后一项这一片段从小到大排列这一操作，这可以由本函数来实现。参数first指的是需要执行排序操作的第一项。
事实上，该函数也可以用递归的方式实现。

找到下一个序列函数next

void next(int list[], int size) {int bigger, biggerx, first;for (int i = size - 2; i >= 0; i--) {first = list[i];bigger = size + 1;for (int j = i + 1; j < size; j++) {if (list[j] > first && list[j] < bigger) {bigger = list[j];biggerx = j;}}if (bigger < size + 1) {swap(&list[i], &list[biggerx]);sort(list, size, i + 1);return;}}
}

该函数的作用是以从小到大的顺序找到下一个排列，不断调用该函数就可以遍历所有的排列，做到不重不漏。具体来说，遍历的方法是从排列的末尾开始作调整，逐步交换，例如：
$$1,2,3\to 1,3,2\to 2,1,3\to 2,3,1\to 3,1,2\to 3,2,1$$
一次next函数相当于实现一个箭头，调用多次即可遍历所有排列情况。

主函数

int main() {int n;printf("n = ");scanf("%d", &n);int nums[n];for (int i = 0; i < n; i++) {nums[i] = i;}int det[n][n];for (int r = 0; r < n; r++) {printf("row %d: ", r + 1);for (int c = 0; c < n; c++) {scanf("%d", &det[r][c]);}}int result = 0, r;while (1) {r = odd_even(nums, n);for (int k = 0; k < n; k++) {r *= det[k][nums[k]];}result += r;if (last(nums, n)) {printf("%d", result);return 0;}else {next(nums, n);}}
}

n是行列式的阶数。本函数默认行列式中的数值均为整数（不限正负），若有必要引入浮点数，只需将程序中的int类型改为double或其他即可。在用户输入行列式各行各列的数值后，程序就会根据行列式的完全展开式进行计算，遍历完所有情形直至last函数的返回值为1为止，输出行列式的值。

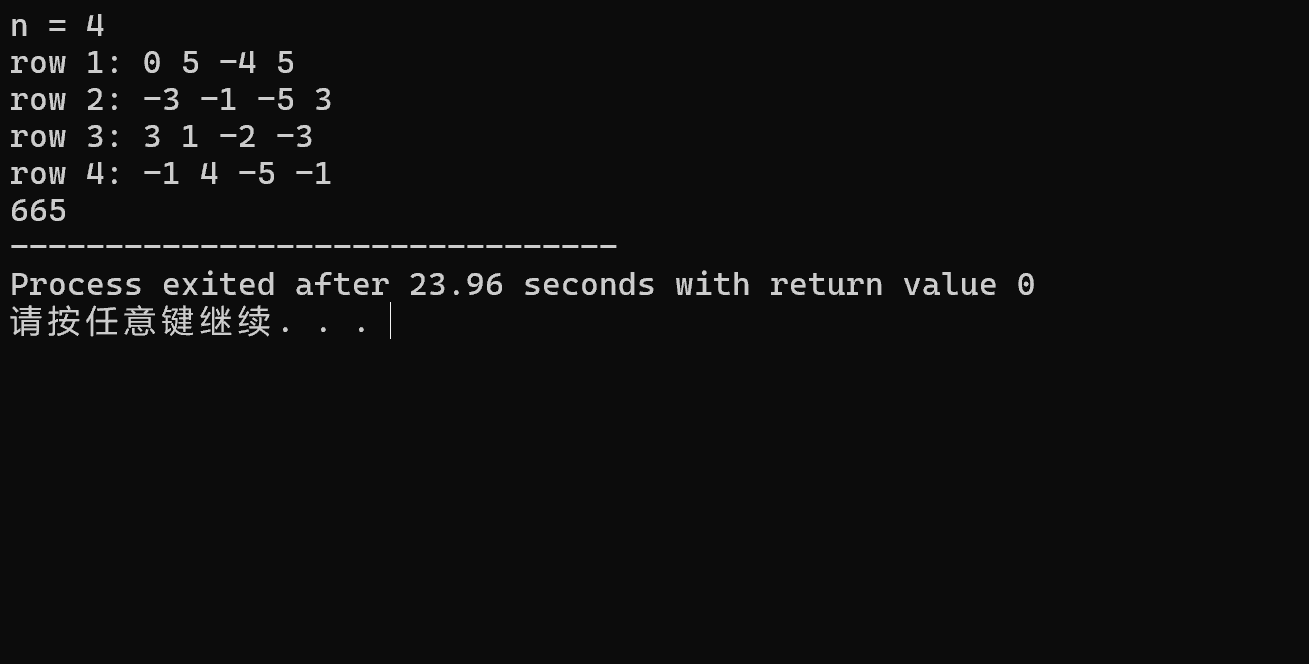
运行结果示例