算法分析:时间和空间复杂度
前言:
算法(Algorithm)是一系列用于处理数据和解决程序问题的系统方法。即使针对同一问题采用不同算法,虽然最终结果可能相同,但其执行过程中的资源消耗和时间效率往往存在显著差异。
如果一个问题的求解算法需要消耗长达一年的时间或则更长,那么这种算法也没什么实际用处。同样,如果一个算法需要1GB或则更大内存,在当前大多数机器上也是无法使用的。
评估一个算法的优劣主要从两个维度考量:
时间复杂度:指算法执行所需的时间消耗。
空间复杂度:指算法执行占用的内存空间大小。
本文将深入探讨时间复杂度和空间复杂度,全面解析算法性能分析方法。

一、时间复杂度
判断一个算法的时间复杂度,很多人首先会想到通过实际运行程序来统计耗时间。
然而这种方法存在明显局限性:运行结果会因机器性能差异而波动,高性能和低性能设备得出的数据可能相差甚远。此外,测试数据的规模也会显著影响结果。更重要的是,在算法设计阶段,我们往往还无法进行完整的运行测试。
时间复杂度的 O 表示法(大 O 表示法,Big O Notation)是描述算法运行时间随输入规模增长而变化的趋势的数学工具,它专注于算法效率的 “数量级”,而非具体的执行时间(如毫秒数)。其核心作用是:在输入规模足够大时,判断算法的效率高低。
1.1大O表示法的定义(了解)
从数学上定义:对于一个算法,若存在常数 c 和整数 n₀,使得当输入规模 n ≥ n₀ 时,算法的运行时间 T(n) ≤ c × f(n),则称该算法的时间复杂度为 O(f(n))。
要理解这部分定义,核心是抓住 “上限”“趋势”“足够大的输入规模” 三个关键词,我们可以通过 “拆解定义 + 具体例子” 的方式,把抽象的数学描述转化为直观的理解。
1.2解析大O表示法(了解)
1.2.1第一步:先明确定义中每个符号的含义
| 符号 | 含义 |
|---|---|
| T(n) | 算法的实际运行时间(比如执行的 “基本操作次数”,如循环次数、比较次数),它是输入规模 n 的函数。 |
| f(n) | 我们选的 “参考函数”(比如 n、logn、n²),用来描述 T (n) 的增长趋势。 |
| c | 一个固定的常数系数(比如 2、5、10),用来 “放大” f (n),确保能覆盖 T (n)。 |
| n | 算法的输入规模(比如数组长度、数据个数)。 |
| n₀ | 一个 “门槛值”—— 当输入规模 n 超过这个值后,“T (n) ≤ c×f (n)” 的关系才稳定成立。 |
1.2.2第二步:用 “具体算法例子” 理解定义
// n是数组长度(输入规模)
void printArray(int arr[], int n)
{ int i; // 1次操作(定义变量,常数项)for (i = 0; i < n; i++){ // 循环n次,每次做1次打印(基本操作)printf("%d ", arr[i]); // 每次循环1次操作}
}1
1. 计算 T (n):算法的实际运行时间
这个算法的 “基本操作” 是 “打印” 和 “循环判断”,我们简化计算(忽略极少量的常数操作,如变量定义):
①循环执行 n 次,每次 1 次打印操作 → 共 n 次基本操作;
②循环判断(i < n)执行 n+1 次,但可近似为 n 次;
因此T(n)可以被近似认为:T(n) ≈ 2n + 1(2n 是循环和打印的总次数,+1 是变量定义的常数项)
2. 找 f (n):选一个 “能描述趋势的参考函数”
T (n) = 2n + 1 的增长趋势由 “n” 决定(当 n 很大时,常数项 1 和系数 2 对增长的影响会越来越小),所以我们选 f(n) = n(线性函数,对应 “线性时间复杂度”)。
3. 找 c 和 n₀:确保 “n ≥ n₀ 时,T (n) ≤ c×f (n)”
我们需要找到一个固定的 c 和 n₀,让 “2n + 1 ≤ c×n” 在 n ≥ n₀ 时成立。
试选 c = 3(只要比 2 大即可,常数系数可以灵活选):此时不等式变为 “2n + 1 ≤ 3n” → 化简得 “1 ≤ n”。
这意味着:当 n ≥ 1(即 n₀ = 1)时,2n + 1 ≤ 3n 恒成立。
再验证一下:
当 n=1 时,T (1)=2×1+1=3,c×f (1)=3×1=3 → 3 ≤ 3(成立);
当 n=10 时,T (10)=2×10+1=21,c×f (10)=3×10=30 → 21 ≤ 30(成立);
当 n=1000 时,T (1000)=2001,c×f (1000)=3000 → 2001 ≤ 3000(成立)。
4. 结论:这个算法的时间复杂度是 O (n)
因为我们找到了常数 c=3 和 n₀=1,当 n≥1 时,T (n) ≤ 3×n,所以根据定义,该算法的时间复杂度为T(n)= O (f (n)) = O (n)。
1.2.3第三步:核心是理解 “上限” 和 “趋势”,而非 “精确值”
O 表示法的本质不是 “计算算法的精确运行时间”,而是 “给算法的运行时间划一个‘不会超过’的上限”,且这个上限只关注 “输入规模增大时的增长趋势”。
1. 为什么说 O (f (n)) 是 “上限”?
比如刚才的遍历算法,O (n) 表示:“当输入规模足够大时,算法的实际运行时间 T (n) 不会超过 n 的某个常数倍”。
它不限制 “T (n) 可以多小”(比如如果数组长度 n=1,T (n)=3,远小于 3×1=3);
只限制 “T (n) 不能多大”(无论 n 多大,T (n) 最多是 3n,不会无限增长)。
2. 为什么可以忽略常数项和低阶项?
比如一个算法的 T (n) = 3n² + 5n + 10,我们会选 f (n)=n²(而非 3n² 或 n²+5n),原因是:当 n 足够大时,高阶项(n²)对 T (n) 的增长起主导作用。
n=10 时,3n²=300,5n=50,10=10 → 高阶项占比 300/(300+50+10)=86%;
n=100 时,3n²=30000,5n=500,10=10 → 高阶项占比 30000/(30000+500+10)=98%;
常数项 10 和 低阶项 5n 的影响会越来越小,甚至可以忽略。
因此,我们只需要用高阶项作为 f (n),再乘以一个常数 c,就能覆盖 T (n) 的增长上限。
1.2.4第四步:避免一个常见误区
“c 和 n₀ 不需要精确计算”,定义只要求 “存在” 这样的 c 和 n₀,不要求我们找到 “最小的 c” 或 “最小的 n₀”。
比如刚才的遍历算法:
选 c=4、n₀=1 也成立。
再验证一下:
当 n=1 时,T (1)=2×1+1=4,c×f (1)=3×1=4 → 3 ≤ 4(成立);
当 n=10 时,T (10)=2×10+1=21,c×f (10)=4×10=40 → 21 ≤ 40(成立);
当 n=1000 时,T (1000)=2001,c×f (1000)=4000 → 2001 ≤ 4000(成立)。
我们不需要纠结 “c 到底是 3 还是 4”,只要知道 “存在这样的 c”,就能确定复杂度的级别(比如 O (n)、O (n²) )。
1.2.5总结:一句话理解
O (f (n)) 的核心是:“当输入规模足够大时,算法的实际运行时间,最多不会超过 f (n) 的某个固定倍数”—— 它用一个简单的函数 f (n),给算法的效率划了一个 “安全上限”,让我们能快速判断不同算法在大规模数据下的性能差距(比如 O (n) 比 O (n²) 快,O (logn) 比 O (n) 快)。
1.3大O表示法的使用(重点)
大O符号(Big O notation)是一种用于描述函数渐进行为的数学符号。在使用大O表示法时,需要遵循以下基本规则:
大O表示法基本规则如下:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
代码示例:
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
步骤 1:拆解代码中的循环结构,该函数包含三个独立的循环结构。
1.嵌套循环
for (int i = 0; i < N; ++i)
{for (int j = 0; j < N; ++j){++count; // 核心操作}
}
①外层循环执行N次
②内层循环在每次外层循环中执行N次
③总执行次数:N × N = N²
2.单重循环
for (int k = 0; k < 2 * N; ++k)
{++count;
}①循环条件为2*N,执行次数与N成正比
②总执行次数:2N
3.while 循环
int M = 10;
while (M--)
{++count; // 核心操作
}①M是固定值 10,与N无关
②总执行次数:10(常数次)
步骤 2:计算总执行次数
将三个循环的执行次数相加,得到总操作次数:
T(n)=N² + 2N + 10。
步骤 3:确定时间复杂度
对于T(n)=N² + 2N + 10。
时间复杂度分析遵循取主导项原则(忽略低阶项和常数系数):当N足够大时,N²是主导项(增长速度远快于2N和常数 10)
因此,时间复杂度为 O(N²)
1.4大O表示法的注意事项(重点)
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
①最坏情况:任意输入规模的最大运行次数(上界)
②平均情况:任意输入规模的期望运行次数
③最好情况:任意输入规模的最小运行次数(下界)
代码示例:在一个长度为N数组中搜索一个数据x
int linearSearch(int arr[], int n, int x)
{for (int i = 0; i < n; i++){ //查找到,直接返回if (arr[i] == x) return i; }return -1; // 未找到
}
分析该查找算法的最好情况、最坏情况、平均情况:
①最好情况:1次找到
②最坏情况:N次找到
③平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
1.5常见时间复杂度计算举例
实例1:计算Func1的时间复杂度
void Func1(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
步骤 1:拆解代码中的循环结构,该函数包含两个独立的循环结构。
1.单重循环
for (int k = 0; k < 2 * N; ++k)
{++count;
}①循环条件为2*N,执行次数与N成正比
②总执行次数:2N
2.while 循环
int M = 10;
while (M--)
{++count; // 核心操作
}①M是固定值 10,与N无关
②总执行次数:10(常数次)
步骤 2:计算总执行次数
将三个循环的执行次数相加,得到总操作次数:
T(n)= 2N + 10。
步骤 3:确定时间复杂度
对于T(n)= 2N + 10。
时间复杂度分析遵循取主导项原则(忽略低阶项和常数系数):当N足够大时,2N是主导项(增长速度远快于常数 10)
因此,时间复杂度为 O(N),其中对于主导项的系数要进行省略。
实例2:计算Func2的时间复杂度
void Func2(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
步骤 1:拆解代码中的循环结构,该函数包含两个独立的循环结构。
1.第一个for循环
for (int k = 0; k < M; ++k){++count;}
2.第二个for循环
for (int k = 0; k < N; ++k)
{++count;
}
步骤 2:计算总执行次数
将两个循环的执行次数相加,得到总操作次数:
T(n)= N + M。
步骤 3:确定时间复杂度
对于T(n)= N + M。
函数有两个独立的输入参数M和N,且两者均为变量(未明确彼此的依赖关系,如M是否是N的函数等),总操作次数由M和N共同决定,需保留两者的影响。
因此时间复杂度为O(M+N)
实例3:计算Func3的时间复杂度
void Func3(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
步骤 1:拆解代码中的循环结构,该函数包含1个独立的循环结构。
int count = 0;for (int k = 0; k < 100; ++k){++count;}
步骤 2:计算总执行次数
循环次数与输入参数N完全无关,无论N取何值(例如N=1、N=1000或N=10000),循环都只执行 100 次。
总操作数为:T(n)=100
步骤 3:确定时间复杂度
对于T(n)=100
当循环次数是固定的常数(与输入规模N无关)时,属于常数级操作。
常数级操作的时间复杂度统一表示为O(1)(忽略具体常数数值,因为它不随输入规模变化)。
实例4:计算冒泡排序的时间复杂度
void BubbleSort(int* a, int n)
{assert(a);//外层循环为冒泡排序的趟数for (size_t end = n; end > 0; --end){int exchange = 0;//内层循环为一趟的比较次数for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
1. 算法核心逻辑拆解
冒泡排序的核心是通过多轮 “冒泡” 将最大元素逐步交换到数组末尾,每轮循环会确定一个元素的最终位置。
代码中:
①外层循环控制 “冒泡” 轮数:end从n递减到1(每轮确定一个元素的位置)。
②内层循环负责本轮的相邻元素比较与交换:i从1遍历到end-1,比较a[i-1]和a[i],若逆序则交换。
③exchange变量用于优化:若某轮未发生交换,说明数组已有序,可提前退出(避免无效循环)。
2. 时间复杂度分析(基于比较 / 交换操作次数)
此时不能简单的看循环的结构进行判断,因为对于不同的输入数组,时间复杂度完全不相同,因此时间复杂度需分最好情况、最坏情况和平均情况讨论:
1.最坏情况
当数组完全逆序时(如[5,4,3,2,1]),每轮都需要交换元素,且无法提前退出:
外层循环执行次数:n-1次(end从n减到2,共n-1轮)。
内层循环执行次数:
第 1 轮:i从1到n-1 → n-1次比较 / 交换。
第 2 轮:i从1到n-2 → n-2次比较 / 交换。
...
第n-1轮:i从1到1 → 1次比较 / 交换。
总操作次数为等差数列求和:T(n)=(n-1) + (n-2) + ... + 1 = n(n-1)/2
主导项为n²/2,因此最坏情况时间复杂度为 O (n²)。
2.最好情况
当数组已经有序时(如[1,2,3,4,5]),优化机制生效:
外层循环仅执行 1 次(第 1 轮)。
内层循环执行n-1次比较(无交换,exchange保持 0),之后直接break退出。
总操作次数为n-1,主导项为n,因此最好情况时间复杂度为 O (n)。
3.平均情况
对于随机排列的数组,大多数情况介于 “完全有序” 和 “完全逆序” 之间。统计意义上,平均需要执行的比较 / 交换次数仍与
n²成正比,因此,平均时间复杂度为 O (n²)。
实例5:二分查找的时间复杂度
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
1. 算法核心逻辑拆解
二分查找的前提是数组a已按升序排序,其核心是通过不断缩小查找区间来定位目标元素x:
始查找区间为[begin, end] = [0, n-1](左闭右闭区间)。
每次循环计算区间中点mid = begin + ((end - begin) >> 1)(等价于(begin + end) / 2,但可避免溢出)。
通过比较a[mid]与x的大小,调整查找区间:
若a[mid] < x:目标在右半区间,更新begin = mid + 1。
若a[mid] > x:目标在左半区间,更新end = mid - 1。
若相等:找到目标,返回mid。
当begin > end时,区间为空,说明目标不存在,返回-1。
2.时间复杂度分析
时间复杂度由最坏情况下的循环执行次数决定(即目标元素不存在,或需要查找到最后一次才找到的情况):
关键观察:每次循环将查找范围 “减半”
初始查找范围大小:[0,n-1]。
我们用 “size_k” 表示第k次循环后剩余的查找范围大小(即当前区间内的元素个数)
初始时:size_0 = n(整个数组的元素个数);
第 1 次循环后:size_1 = size_0 / 2 = n/2;
第 2 次循环后:size_2 = size_1 / 2 = n/(2²);
第 3 次循环后:size_3 = size_2 / 2 = n/(2³);
...
第k次循环后:size_k = n/(2^k)
温馨提示:
这里的除法是 “逻辑减半”,实际会向上取整。比如n=5时,第 1 次循环后size_1=2,而非2.5,但推导时先简化为n/(2^k),不影响核心趋势。
数学公式推导:
临界条件为:begin==end,所以终止条件为begin>end。
只有当size_k ≤ 1时,再执行一次循环才会让范围为空(终止)。因此,最坏情况的循环次数k,是 “将范围从n减半到≤1所需的最少次数”。
由此可得出不等式:k ≥ log₂n
所以T(n)=log₂n ,故而时间复杂度被认为是O(logN)
3.对于二分查找次数的加深理解
推导得到k ≥ log₂n,但k必须是整数(循环次数只能是 1 次、2 次...,不能是 3.17 次)。因此,k是满足 “k ≥ log₂n” 的最小整数—— 这就是 “向上取整” 的本质。
用 3 个典型例子验证:
例子 1:n=8
log₂8 = 3,满足k ≥ 3的最小整数是 3。
实际循环过程(最坏情况,目标不在数组中):初始范围 8 → 第 1 次循环后 4 → 第 2 次后 2 → 第 3 次后 1 → 第 3 次循环判断 1 个元素,没找到 → begin>end,终止。总循环次数k=3,正好等于log₂n,无需向上取整。
例子 2:n=9log₂9≈3.17,满足k ≥ 3.17的最小整数是 4。
实际循环过程:初始范围 9 → 第 1 次后 5(9/2≈4.5,向上取整为 5) → 第 2 次后 3(5/2≈2.5→3) → 第 3 次后 2(3/2≈1.5→2) → 第 4 次后 1(2/2=1) → 第 4 次判断 1 个元素,没找到 → 终止。总循环次数k=4,是log₂9≈3.17的向上取整。
例子 3:n=5
log₂5≈2.32,满足k ≥ 2.32的最小整数是 3。
实际循环过程:初始 5 → 第 1 次后 3(5/2≈2.5→3) → 第 2 次后 2(3/2≈1.5→2) → 第 3 次后 1(2/2=1) → 第 3 次判断后终止。总循环次数k=3,是log₂5≈2.32的向上取整。
实例6:阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
1. 递归逻辑拆解
该函数的递归关系为:
当N = 0时(base case),直接返回 1,无递归调用;
当N > 0时,返回Fac(N-1) * N,即需要先递归调用Fac(N-1),再将结果与N相乘。
这种递归是线性递归(每次调用只产生一个新的递归调用),不存在分支或重复计算。
调用链条是单向递减的:Fac(N) → Fac(N-1) → Fac(N-2) → ... → Fac(0)
2. 时间复杂度分析(基于递归调用次数)
时间复杂度由总递归调用次数决定(每次调用的核心操作是常数级的乘法和判断,时间为O(1)):
计算Fac(N)需要调用Fac(N-1);
计算Fac(N-1)需要调用Fac(N-2);
...
直到Fac(0),无需再递归,直接返回 1。
总调用次数为N + 1次(从Fac(N)到Fac(0),共N+1个函数调用)。
由于每次调用的操作是O(1),总时间复杂度为:(N + 1) × O(1) = O(N)
示例7:用递归求解斐波那契数列的时间复杂度
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
1.递归树分析
函数的递归定义为:
当N < 3时(base case),直接返回 1,无递归调用;
当N ≥ 3时,返回Fib(N-1) + Fib(N-2),即每次调用需要先递归计算Fib(N-1)和Fib(N-2),再将结果相加。
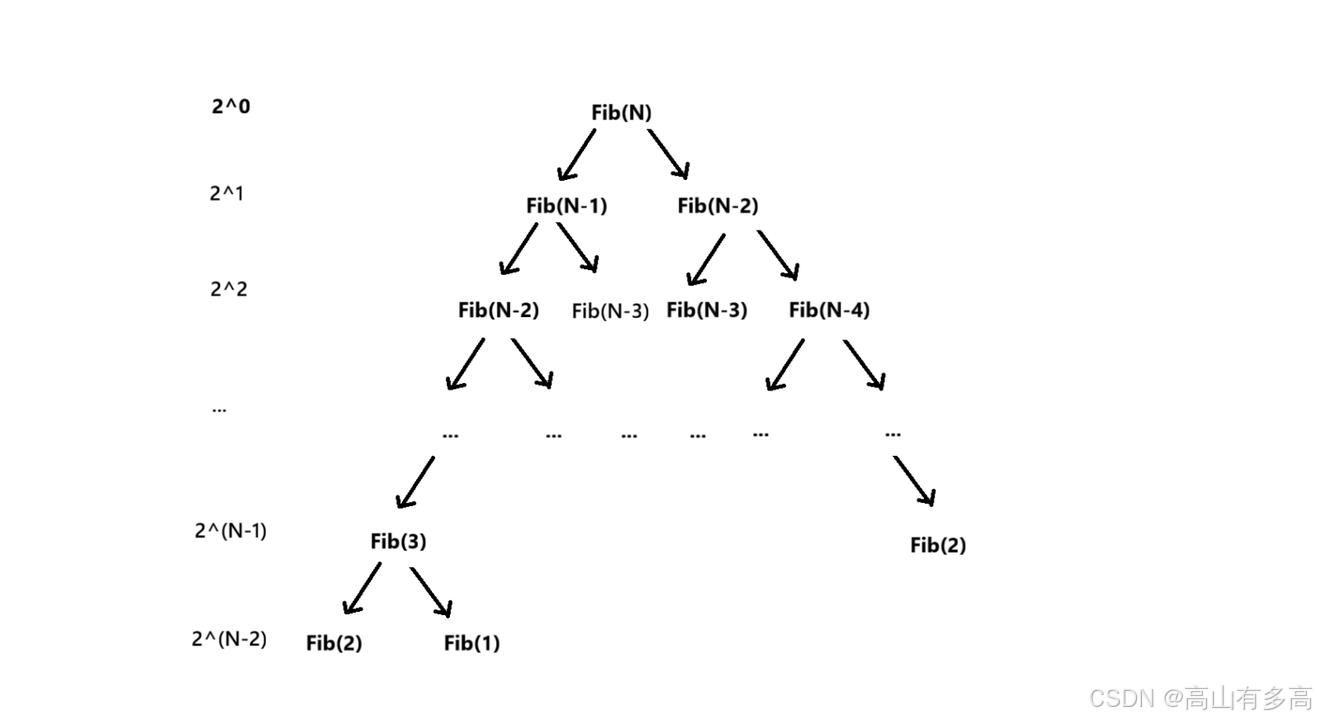
这种 “分支式递归” 会形成一棵递归树,每个节点Fib(N)(k ≥ 3)都会产生两个子节点Fib(N-1)和Fib(N-2),直到触达Fib(2) 和 Fib(1)。
2.时间复杂度
节点数量规律:第一层递归树有1个节点,第二层递归树有2个节点,第三层递归树有4个节点,以此类推,到最后一层递归树有2^(N-2)个节点
总节点数近似为等比数列求和:1 + 2 + 4 + ... + 2ⁿ⁻¹ = 2ⁿ - 1。
故而时间复杂度为O(2ⁿ)
二、空间复杂度
2.1空间复杂度的基本概念
时间复杂度不是用来计算程序具体耗时的,那么我们也应该明白,空间复杂度也不是用来计算程序实际占用空间,事实上空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是计算程序占用了多少字节的空间,因为这个也没太大意义,事实上空间复杂度计算的是变量的个数,空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
温馨提示:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因 此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
2.2常见空间复杂度的计算
示例一:冒泡排序的空间复杂度
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}空间复杂度衡量的是算法额外占用的临时存储空间(不包括输入数据本身的存储)。
在BubbleSort中:
仅使用了少量固定大小的局部变量:end(循环控制变量)、exchange(标记是否发生交换)、i(内层循环控制变量)。
这些变量的存储空间大小是固定的(与输入数组的规模n无关)。
没有动态分配内存(如malloc/new创建的数组、对象等),也没有递归调用(无需考虑递归栈空间)。
交换操作(Swap函数)通常仅使用常数空间的临时变量(用于交换两个元素),不会引入与n相关的额外空间。
故而冒泡排序的空间复杂度为O(1)
示例二:计算斐波那契数列的空间复杂度
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}
空间复杂度衡量的是算法额外占用的临时存储空间(不包括输入数据本身的存储)。
动态分配的数组fibArray大小为n+1
局部变量(如i、fibArray指针)占用固定大小的空间,为O(1)
无递归调用(无需递归栈空间),无其他动态分配操作
故而总空间复杂度由数组fibArray的大小决定,即O(n)。
示例三:计算阶乘递归Fac的空间复杂度
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}递归函数的空间复杂度主要取决于递归调用栈的最大深度:
每次递归调用会在栈上创建一个栈帧,保存参数N、返回地址等信息,函数返回后栈帧释放。
对于阶乘递归需要调用Fac(N)→ Fac(N-1)→Fac(N-2)→...→Fac(0)
所以需要创建N+1个栈帧,故而空间复杂度为O(N+1)
三、常见复杂度对比
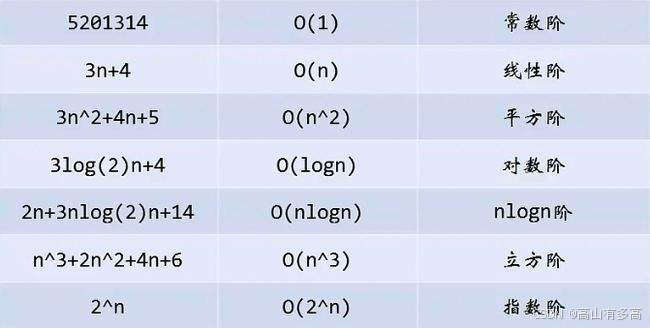
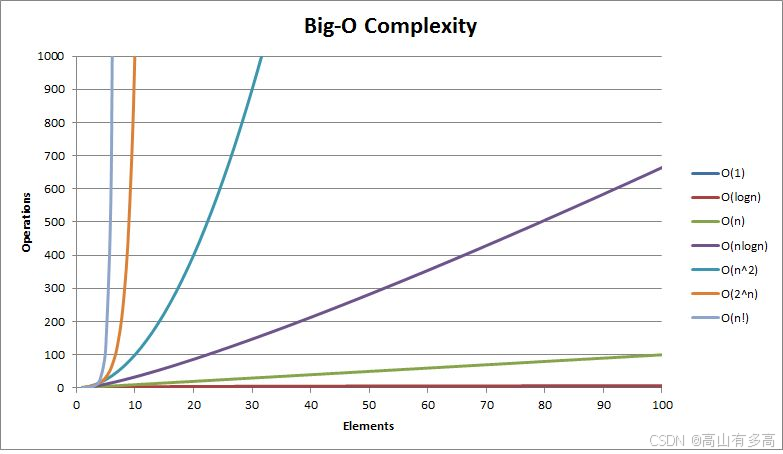
3.1常见的时间复杂度:
3.2常见的空间复杂度
| 复杂度类型 | 增长特点 | 核心依据 | 典型实例 | 空间效率 |
|---|---|---|---|---|
| O(1) | 空间固定,与n无关 | 仅用常数个局部 / 临时变量
无动态分配、无递归栈(或递归深度固定) | 1. 冒泡排序( 2. 数组求和: 3. 迭代版斐波那契(仅存前两个数: | 最高 |
| O(n) | 空间与n成正比,线性增长 | 动态分配长度为 或递归深度为 | 1. 动态数组版斐波那契 ( 2. 递归版阶乘( | 中等 |
| O(n²) | 空间随n²增长,增长较快 | 动态分配n×n的二维数组,或嵌套递归的栈深度为n² | 1. 创建n×n的数组 | 较低 |
既然看到这里了,不妨点赞+收藏,感谢大家,若有问题请指正。