离散与连续随机变量
一、离散型随机变量
连续与离散随机变量(数值化实验的各种结果)
离散型随机变量

连续型随机变量
1.1 离散型随机变量的概率函数(概率质量函数)
专为离散型随机变量定义的:p(x)=Prob(X=x)p(x)=Prob(X=x)p(x)=Prob(X=x)
本身就是一个概率值,XXX是随机变量的取值,PPP就是概率。
比如我们来投掷骰子

1.2 离散型随机变量的概率分布
离散型随机变量概率分布的核心是:
- 找到离散型随机变量XXX的所有可能取值;
- 得到离散型随机变量取这些值的概率
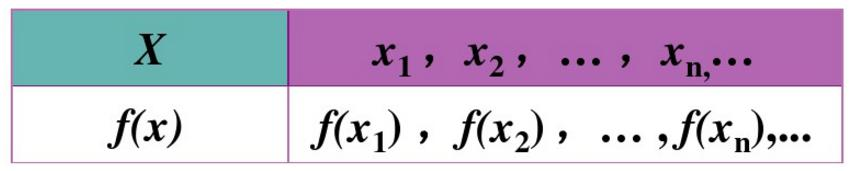
f(xi)≥0,i=1,2,...f\left(x_{i}\right) \geq 0, i=1,2, ...f(xi)≥0,i=1,2,...
∑f(xi)=1\sum f\left(x_{i}\right)=1∑f(xi)=1
f(xi)=P(X=xi)f(x_{i})=P(X=x_{i})f(xi)=P(X=xi)为离散型随机变量的概率函数。
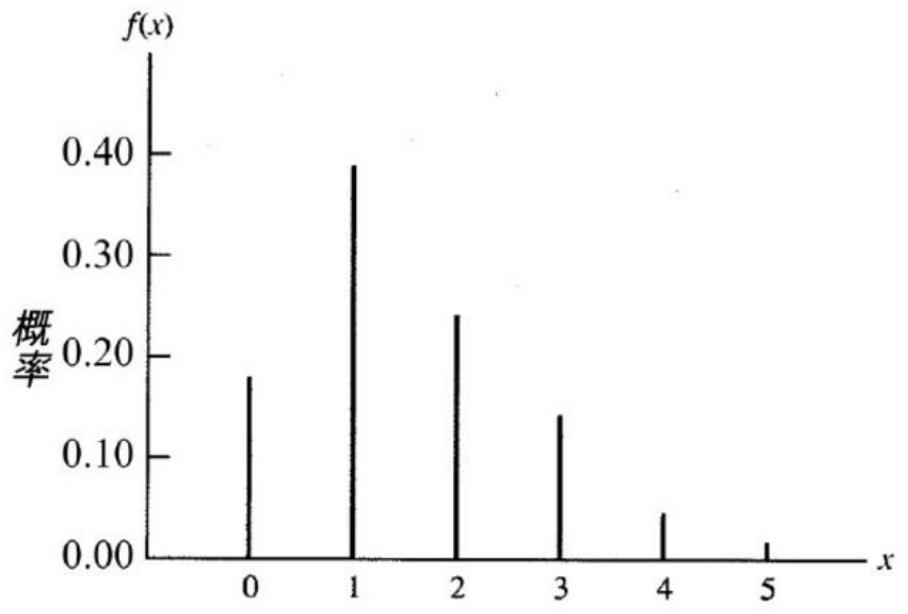
示例:房间中介一天卖出房源数量

二、连续型随机变量
2.1 连续型随机变量的概率密度引入
概率密度:对于连续型随机变量X,我们不能给出其取每一个值的概率 也就是画不出那个分布表,这里我们选择使用密度来表示其概率分布!
假设我有一组零件,由于各种因素的影响,其长度是各不相同的。
129, 132, 136, 145, 140, 145, 147, 142, 138, 144, 147, 142, 137, 144, 144, 134, 149, 142, 137, 137, 155, 128, 143, 144, 148, 139, 143, 142, 135, 142, 148, 137, 142, 144, 141, 149, 132, 134, 145, 132, 140, 142, 130, 145, 148, 143, 148, 135, 136, 152, 141, 146, 138, 131, 138, 136, 144, 142, 142, 137, 141, 134, 142, 133, 153, 143, 145, 140, 137, 142, 150, 141, 139, 139, 150, 139, 137, 139, 140, 143, 149, 136, 142, 134, 146, 145, 130, 136, 140, 134, 142, 142, 135, 131, 136, 139, 137, 144, 141, 136
2.2 连续型随机变量的概率密度函数
步骤1:数据分组
离散型的我们已经知道咋办啦,那按照这个思路我们先简单分个组
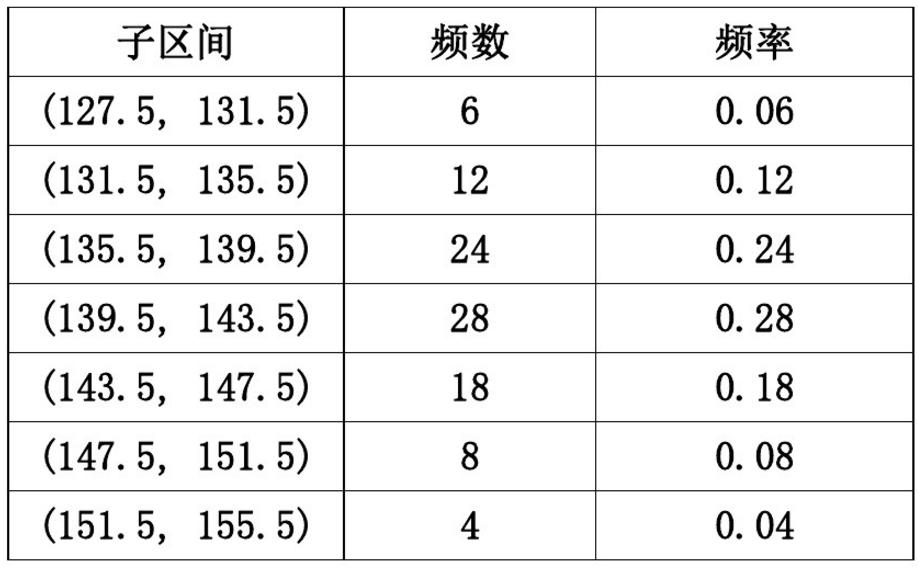
这样看起来问题好像可以解决啦!
步骤2:绘制频率分布直方图
绘制频率分布直方图

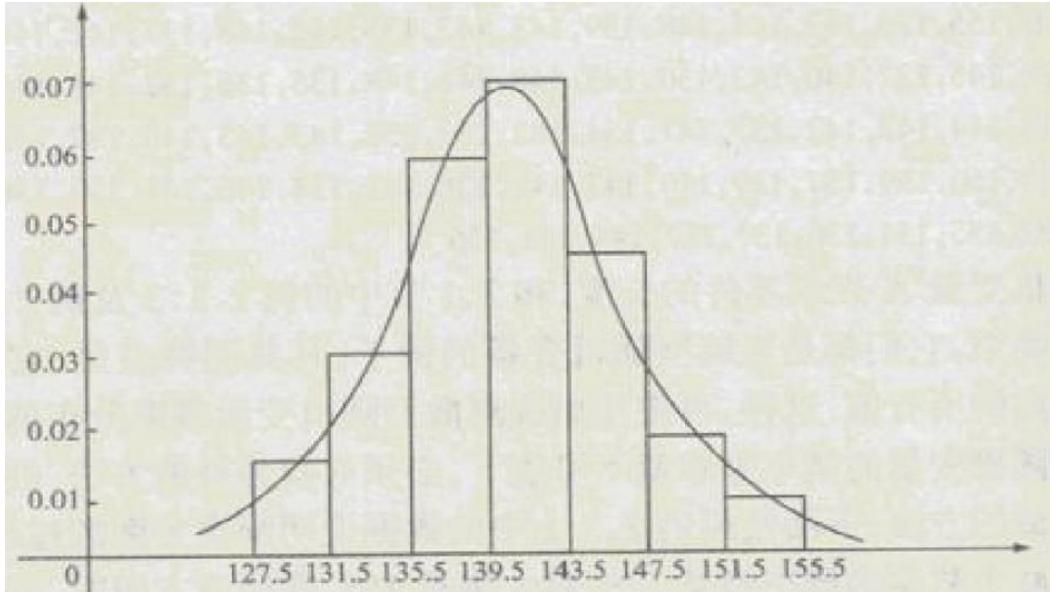
这样看起来有点粗糙,当我们把样本数据增加,分组数也同时增加,这样的
轮廓是不是会越来越细致呀!接近于一条曲线,这不就是我们想要的嘛!
概率密度函数的定义与意义
-
类比理解:
密度:一个物体,我们如果问其中一个点的质量是多少?这该怎么求呢?
由于这个点实在太小了,那么质量就为0了。但是其中的一大块是由很多个点组成的,这时我们就可以根据密度来求其质量了! -
数学表达:设XXX为连续型随机变量,XXX在任意区间(a,b](a,b](a,b]上的概率可表示为:
P(a<X≤b)=∫abf(x)dxP(a<X \leq b)=\int_{a}^{b} f(x) dxP(a<X≤b)=∫abf(x)dx
其中,f(x)f(x)f(x)称为XXX的概率密度函数(简称“密度”)。
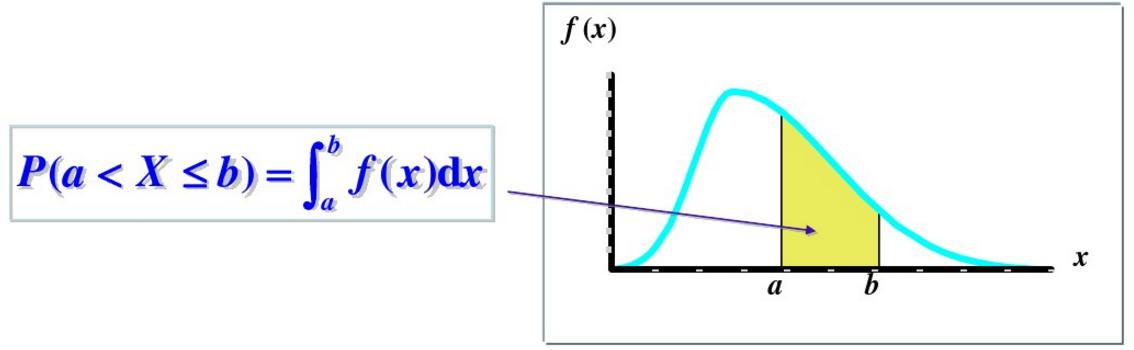
- 几何意义:概率密度函数用数学公式表示就是一个积分,也可以把概率形象的说成面积!
概率密度函数与分布函数的关系
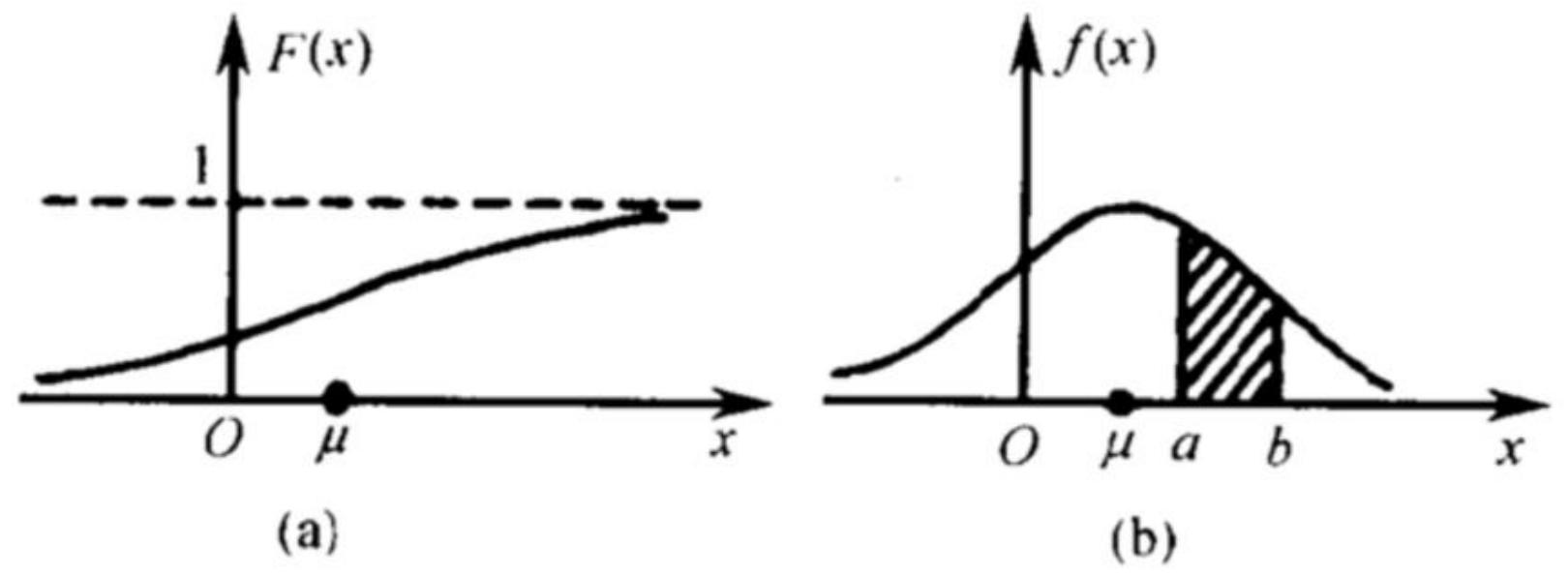
- 图(a):连续型随机变量的分布函数F(x)F(x)F(x)(表示P(X≤x)P(X \leq x)P(X≤x));
- 图(b):连续型随机变量的概率密度函数f(x)f(x)f(x)(分布函数F(x)F(x)F(x)的导数)。
2.3 连续型随机变量的简单随机抽样
简单随机抽样的样本需满足以下两个条件:
-
独立性:样本X1,X2,…,XnX_1,X_2,\dots,X_nX1,X2,…,Xn是相互独立的随机变量,其联合分布函数为:
F(x1,x2,⋯ ,xn)=∏i=1nF(xi)F(x_{1}, x_{2}, \cdots, x_{n})=\prod_{i=1}^{n} F(x_{i})F(x1,x2,⋯,xn)=i=1∏nF(xi) -
同分布性:样本X1,X2,…,XnX_1,X_2,\dots,X_nX1,X2,…,Xn与总体XXX同分布,其联合概率密度为:
f(x1,x2,⋯ ,xn)=∏i=1nf(xi)f(x_{1}, x_{2}, \cdots, x_{n})=\prod_{i=1}^{n} f(x_{i})f(x1,x2,⋯,xn)=i=1∏nf(xi)
