从直线到环形：解锁栈、队列背后的空间与效率平衡术

0. 引言

在计算机世界里，最朴素的存储模型莫过于数组。它是一条线，拥有起点与终点，能够精确定位到每一个下标。看似简单，却衍生出两种最经典的数据结构：栈（stack） 和 队列（queue）。

但你会发现，这两位“老朋友”虽然好用，却并不完美：空间利用不足、判定复杂、甚至会出现“假溢出”。直到某一天，人们在数组的直线尽头，轻轻地把两端接了起来，一种更优雅的结构——循环队列（circular queue）——就此诞生。

这不仅是一段算法的演化史，更是一段“如何从浪费走向优雅”的故事

---

1. 栈：直线的极简哲学

栈的哲学很简单：后进先出（LIFO）

可以把它想象成一摞盘子，如果你想拿最下面那只盘子，必须先把上面的盘子一一移走。这种规则简单却极其常见。我们将盘子替换为各种类型的元素，就得到了栈这种数据结构。

栈只从顶部即栈顶出入数据，入数据称为压栈 ，出数据称为出栈，如图：

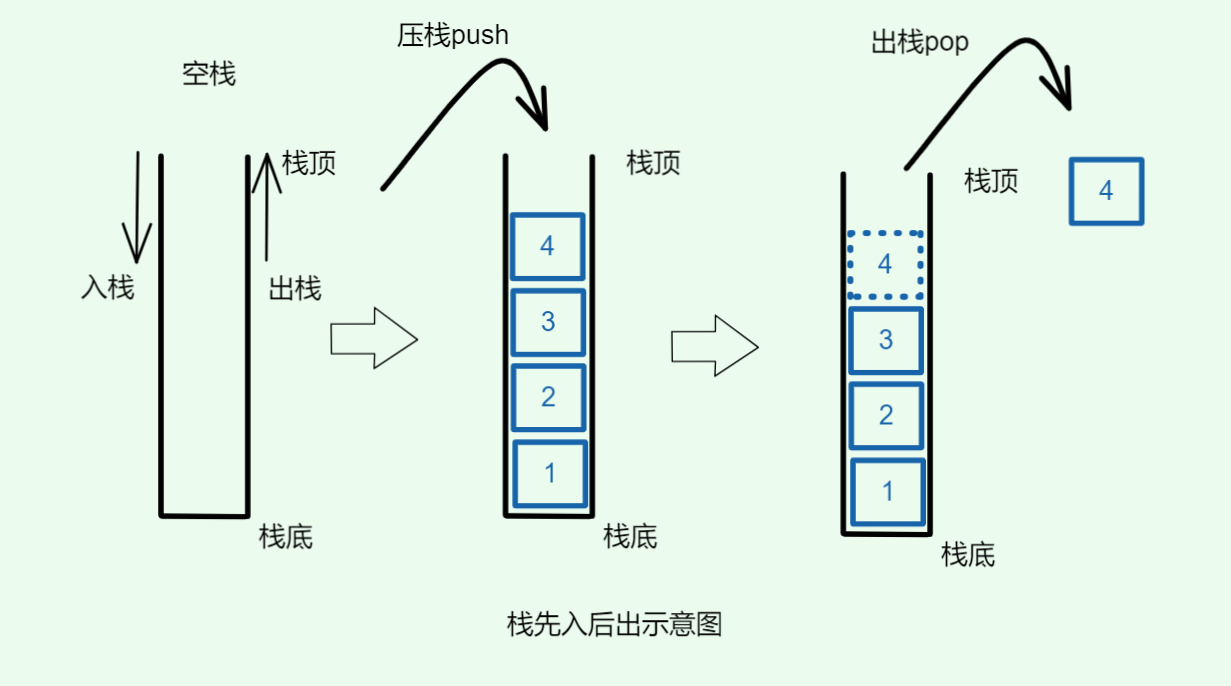
1.1. 栈的核心特性

• 顺序特性： 后进先出（LIFO, Last In First Out）
• 核心接口：

​ push(val): 入栈操作，将元素压入栈顶

​ pop(): 出栈，移除栈顶元素

​ top(): 获取栈顶元素

​ empty(): 判断栈是否为空

​ size(): 返回栈中元素个数

栈的操作都围绕栈顶展开，所有操作时间复杂度在理想情况都为$O(1)$

---

1.2. 底层实现线路

栈可以用两种方式实现：

1. 动态数组： 利用数组随机访问的特性，栈顶对应数组的末尾，扩容时进行拷贝
2. 链表： 每次操作在链表头部完成，不用扩容，但是内存分散，缓存不友好

我们选择用动态数组实现。

核心成员变量：

• _arr: 动态数组存储元素
• _top_index: 当前栈顶索引（初识空栈为-1）
• _capacity: 容量，空间满自动扩容

---

1.3. 核心接口实现

template <class T>
class mini_stack {
private:T* _arr; // 动态数组存储数据int _top_index; // 栈顶索引size_t _capacity; // 当前容量// 扩容void resize() {size_t new_cap = _capacity == 0 ? 4 : 2 * _capacity;// 开一个新容量的空间T* tmp = new T[new_cap];// 将_arr的内容拷贝到新空间（只需复制有效元素，即[0, _top_index]范围）for (size_t i = 0; i < _top_index; i++){tmp[i] = _arr[i];}delete[] _arr;_arr = tmp;_capacity = new_cap;}public:// 构造mini_stack(size_t initial_capacity = 4):_arr(new T[initial_capacity]),_top_index(-1),_capacity(initial_capacity){}// 拷贝构造 深拷贝mini_stack(const mini_stack<T>& other)  : _arr(nullptr), _top_index(-1), _capacity(0){// 1. 分配与原对象相同大小的内存_capacity = other._capacity;if (_capacity > 0) {_arr = new T[_capacity];// 2. 复制元素（只需复制有效元素，即[0, _top_index]范围）for (size_t i = 0; i <= other._top_index; ++i) {_arr[i] = other._arr[i];}}// 3. 复制栈顶索引_top_index = other._top_index;}// 入栈void push(const T& val) {// 判断是否需要扩容if (_top_index + 1 == _capacity) resize();// 压栈_arr[++_top_index] = val;}// 出栈void pop() { assert(!empty()); --_top_index; }// 获取栈顶元素T& top() { assert(!empty());  return _arr[_top_index]; }// 判空bool empty() { return _top_index == -1; }// 有效元素个数size_t size() { return _top_index + 1; }// 容量size_t capacity() const { return _capacity; }// 清理元素但不改变容量void clear() { _top_index = -1; }// 打印栈void print_stack() {if (_top_index == -1)cout << "此栈为空" << endl;elsefor (size_t i = 0; i <= _top_index; i++){cout << _arr[_top_index] << " ";}cout << endl;}
};

---

1.4. 栈的使用场景

• **浏览器中的后退与前进、软件中的撤销与反撤销： **每当我们打开新的网页，浏览器就会对上一个网页执行入栈，这样我们就可以通过后退操作回到上一个网页。后退操作实际上是在执行出栈。如果要同时支持后退和前进，那么需要两个栈来配合实现。
• 程序内存管理： 每次调用函数时，系统都会在栈顶添加一个栈帧，用于记录函数的上下文信息。在递归函数中，向下递推阶段会不断执行入栈操作，而向上回溯阶段则会不断执行出栈操作。

栈的存在，让“顺序操作”变得极简优雅。

---

2. 普通队列：公平的标榜

队列的哲学是：先进先出（FIFO, First In First Out）。

它就像排队买奶茶，先来的同学先买走，后来的乖乖排在后面。这种逻辑广泛存在于任务调度、打印服务、订单处理等场景中。

而把排队的人换成各种类型，就形成了数据结构的队列

如图：

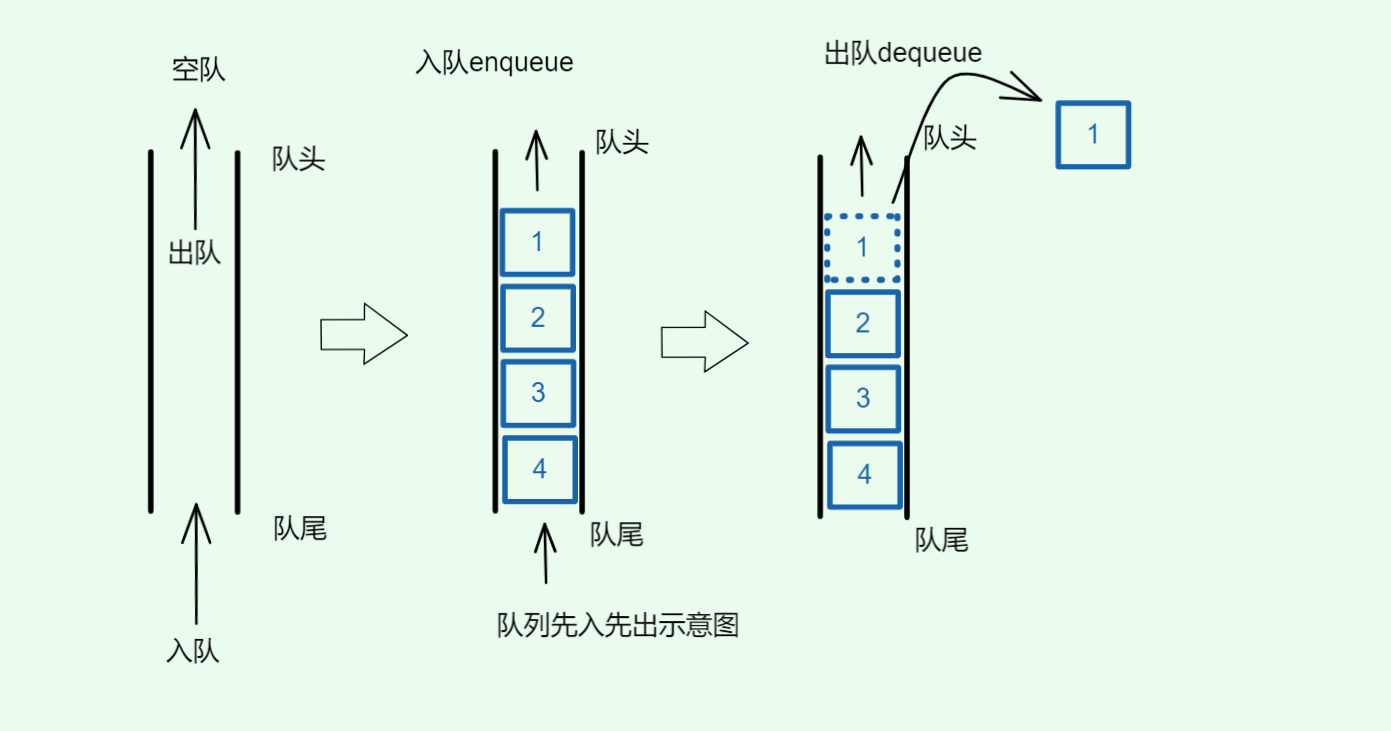
2.1. 队列的核心特性

• 顺序特性： 先进先出（FIFO,First In First Out）

• 核心接口：

  ​ enqueue(val): 入队，加入队尾

  ​ pop(): 出队，删除队首

  ​ front: 获取队首元素

  ​ back: 获取队尾元素

  ​ empty(): 判断队列是否为空

  ​ size(): 返回队列中元素个数

---

2.2. 底层实现思路

队列有两种常见实现：

1. 链表：队首删除、队尾插入 → 逻辑简单，都是 O(1)。
2. 数组：通过两个索引标记头尾。但这里会遇到一个问题：

假溢出：如果你用数组实现队列，先入队几次，再出队几次，队首不断前移，前面的空间空出来了，但是尾部到头尾依然是满的，于是会发现：明明有空位，元素却不能入队，如图：

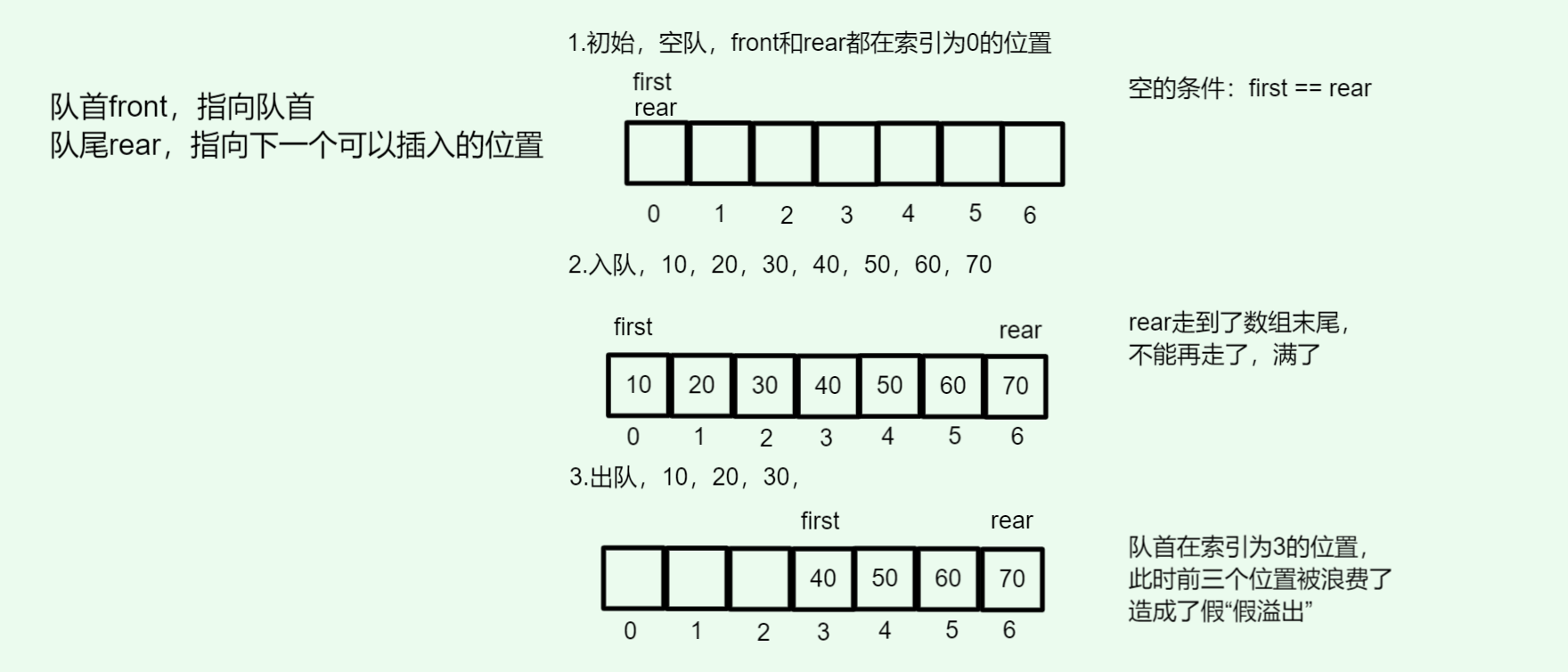
这就是普通数组队列的最大痛点。

我们采用单链表控制：

_head: 队首指针

_tail: 队尾指针

_size(): 元素数量

---

2.3. 核心接口实现

// 链表类
template <class T>
struct list_node {list_node* _next;T _val;list_node(const T& val = T()):_next(nullptr),_val(val){ }
};// 队列类
template <class T>
class mini_queue {
private:list_node<T>* _head; // 队首list_node<T>* _tail; // 队尾size_t _size;public:// 构造mini_queue():_head(nullptr),_tail(nullptr),_size(0){ }// 拷贝构造mini_queue(const mini_queue& other):_head(other._head), _tail(other._tail), _size(other._size){// 遍历原链表 逐个复制list_node<T>* cur = other._head;while (cur != nullptr) {// 创建新节点（复制当前节点的数据）list_node<T>* new_node = new list_node<T>(cur->_val);// 如果是空队列 新的节点既是队首 又是队尾if (_head == nullptr) {_head = _tail = new_node;}else {// 将新节点连接到_tail_tail->_next = new_node;// 更新队尾_tail = new_node;}++_size;cur = cur->_next;}}// 析构~mini_queue() { clear(); }//  入队 尾插void enqueue(const T& val) {list_node<T>* new_node = new list_node<T>(val);// 空队列 新元素既是队首 也是队尾if (_head == nullptr) {_head = _tail = new_node;}else {_tail->_next = new_node;_tail = new_node;}++_size;}// 出队 头删void dequeue() {assert(!empty());// 保存当前队首节点（待删除）list_node<T>* tmp = _head;// 队列只有一个元素if (_head == _tail) {_head = _tail = nullptr;  // 删完后队列空，头尾都置空}else {// 多个元素：头指针后移到下一个节点_head = _head->_next;}delete tmp;  // 删除原来的队首节点--_size;     // 队列大小减1}// 获取队首队尾元素const T& front() const { assert(!empty()); return _head->_val; }const T& back() const { assert(!empty()); return _tail->_val; }// 判空const bool empty() const { return _size == 0; }// 队列元素个数const size_t size() const { return _size; }// 清空队列void clear() { while (!empty()) dequeue(); }// 打印队列void print_queue() {if (empty()) {std::cout << "此队列为空" << std::endl;return;}list_node<T>* cur = _head;while (cur) {std::cout << cur->_val << " ";cur = cur->_next;}std::cout << std::endl;}
};

---

2.4. 队列的使用场景

• 淘宝订单： 购物者下单后，订单将加入队列中，系统随后会根据顺序处理队列中的订单
• **各类待办事项：**任何需要实现“先来后到”功能的场景，例如打印机的任务队列、餐厅的出餐队列等。

---

3. 循环队列：从空间浪费到优雅的满队判定

为了消除 假溢出，人们做了一个小动作： 把数组的尾巴接到头部，形成一个环。

于是，队首出队空出来的位置，可以被队尾重新利用。如图：

---

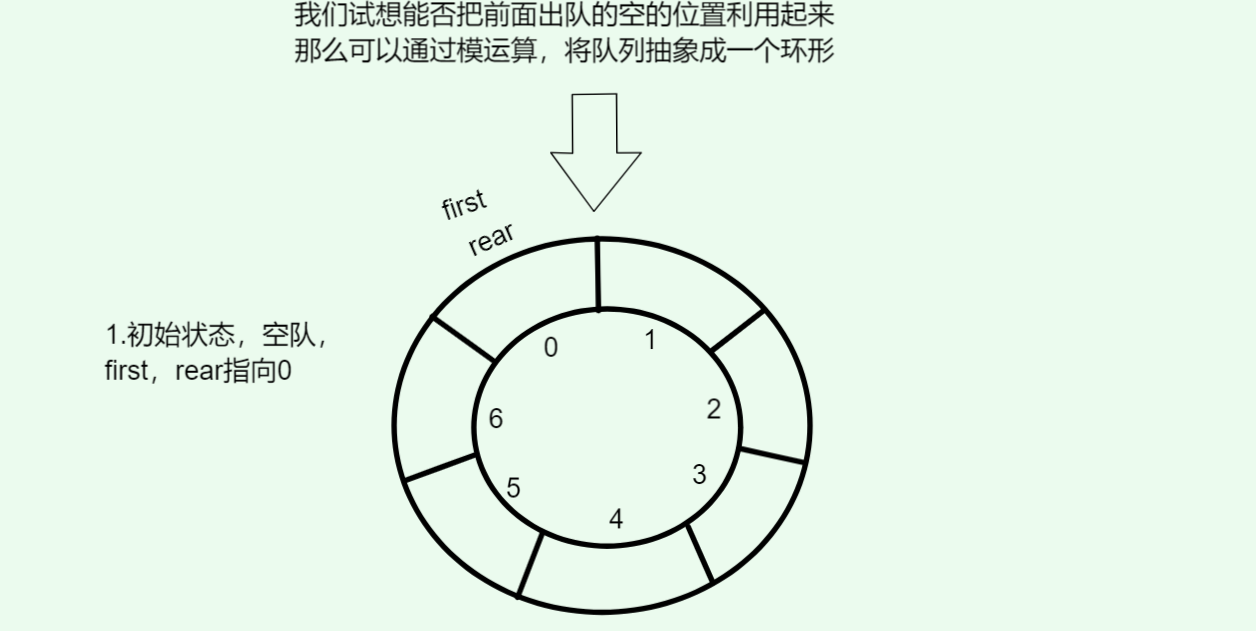
3.1. 关键设计

把前面出队的空的位置利用起来，那么可以通过模运算，将队列抽象成一个环形

用两个索引：front 指向队首，rear 指向下一个插入位置。

插入时：rear = (rear + 1) % capacity

删除时：front = (front + 1) % capacity

判空：front == rear

判满：(rear + 1) % capacity == front

敲黑板！！！

为了区分空和满，必须浪费一个空间

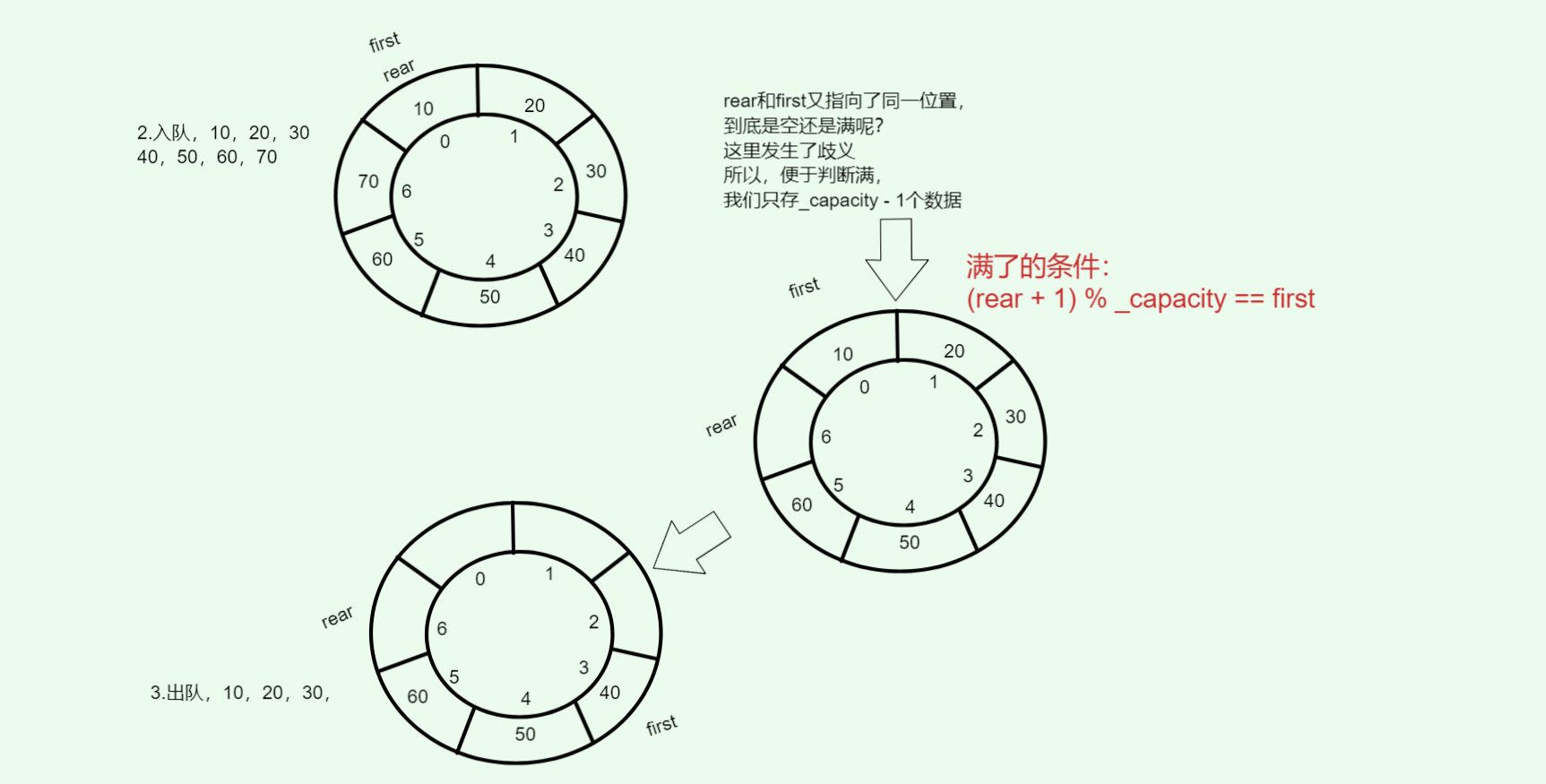
这就是循环队列的经典设计：数组容量为 n，但最多只能放 n-1 个元素。

---

3.2. 动态扩容

实际工程中，队列可能会越来越大，所以我们要支持 动态扩容：

1. 当队列满时，开辟 2 倍容量的新数组。
2. 按顺序把旧数据搬过去（注意队列可能被环绕，要小心拆成两段复制）。
3. 重置 front = 0，rear = size。

这样，循环队列就兼顾了 空间利用率 与 灵活扩展性。

---

3.3. 代码实现

template <class T>
class circular_queue {
private:T* _arr; // 底层动态数组控制size_t _front; // 队首索引size_t _rear; // 队尾索引，指向队列最后一个元素的下一个位置size_t _capacity; // 数组总容量 实际只能存储_capacity - 1个元素// 扩容void resize() {size_t new_cap = _capacity == 0 ? 4 : 2 * _capacity;T* tmp = new T[new_cap];// 计算原队列元素个数 防止负数的情况size_t count = (_rear - _front + _capacity) % _capacity;size_t cur = _front;for (size_t i = 0; i < count; i++){tmp[i] = _arr[cur];cur = (cur + 1) % _capacity;}delete[] _arr;_arr = tmp;_capacity = new_cap;_front = 0;_rear = count; // 新队列队尾指向最后一个元素的下一个位置（无预留空位，后续入队会自动留）}public:// 构造 circular_queue(size_t capacity = 4):_front(0), _rear(0), _capacity(capacity){_arr = new T[_capacity];}// 拷贝构造circular_queue(const circular_queue& other):_front(other._front), _rear(other._rear), _capacity(other._capacity){_arr = new T[_capacity];for (size_t i = 0; i < _capacity; i++){_arr[i] = other._arr[i];}}// 析构 ~circular_queue() {delete[] _arr;_arr = nullptr;_front = _rear = 0;_capacity = 0;}// 入队 尾插void enqueue(const T& val) {// 判断是否满了if ((_rear + 1) % _capacity == _front)resize();_arr[_rear] = val;_rear = (_rear + 1) % _capacity;}// 出队 头删void dequeue() {// 确保队列不为空assert(!empty());// 调整_front的指向即可_front = (_front + 1) % _capacity;}// 获取队首元素const T& front() const { assert(!empty()); return _arr[_front]; }// 获取队尾元素const T& back() const {assert(!empty());// 解决rear=0的负数问题size_t tail_idx = (_rear - 1 + _capacity) % _capacity;return _arr[tail_idx];}// 判断队列是否为空const bool empty() const { return _front == _rear; }// 判断队列是否满了const bool full() const { return (_rear + 1) % _capacity == _front; }// 计算有效元素个数const size_t size() const { return (_rear - 1 + _capacity) % _capacity; }// 计算队列容量const size_t capacity() const { return _capacity; }// 清空队列void clear() { _front = 0; _rear = 0; }// 打印队列void print_circular_queue() {if (empty()) {std::cout << "队列为空" << "\n";return;}// 先算元素个数再打印size_t count = size();size_t cur = _front;for (size_t i = 0; i < count; i++){std::cout << _arr[cur] << " ";cur = (cur + 1) % _capacity;}std::cout << "\n";}};

这里需要注意一点：避免负数的情况
在这里插入图片描述

---

3.4. 循环队列的使用场景

1. 操作系统就绪队列： 按 FIFO 调度进程 / 线程，$O(1)$ 入队出队，缓存友好
2. IO 缓冲区（磁盘 / 网络 / 串口）： 暂存读写速度不匹配的数据，避免假溢出

---

4. 总结：基础数据结构的 “进化” 与 “取舍”

从数组这条 “直线” 出发，我们走过栈的 “极简秩序”、普通队列的 “公平逻辑”，最终在循环队列的 “环形智慧” 里，找到空间与效率的平衡。这背后，是关于 “解决问题” 的技术思考：
栈以 “后进先出”（LIFO） 将顺序操作做到极致 —— 放弃随机访问，只保留栈顶读写，换来 O (1) 效率，成为函数调用、撤销操作的优选；普通队列用 “先进先出”（FIFO） 贴合排队需求，但数组实现的 “假溢出” 提醒我们：没有完美结构，只有适配场景。链表解决了假溢出，却带来缓存问题，可见技术选择本是 “取舍” 的艺术；循环队列则优化了这种取舍：它保留数组的连续内存优势，用 “预留一个空位” 区分空满、“模运算” 实现环形复用，再靠动态扩容打破容量限制 —— 不推倒重来，只精准修复痛点。
本质上，这三种基础结构的价值远超代码：从场景提炼规则（如 LIFO/FIFO）、发现方案痛点（如假溢出）、用设计平衡矛盾，这些思考会成为理解复杂结构、做好工程选择的基石。毕竟，复杂系统源于对基础的深刻理解，优雅技术始于对 “不完美” 的持续优化。