考研复习-线性代数强化-向量组和方程组特征值
两个矩阵秩的结论,以及判断向量组是否相关
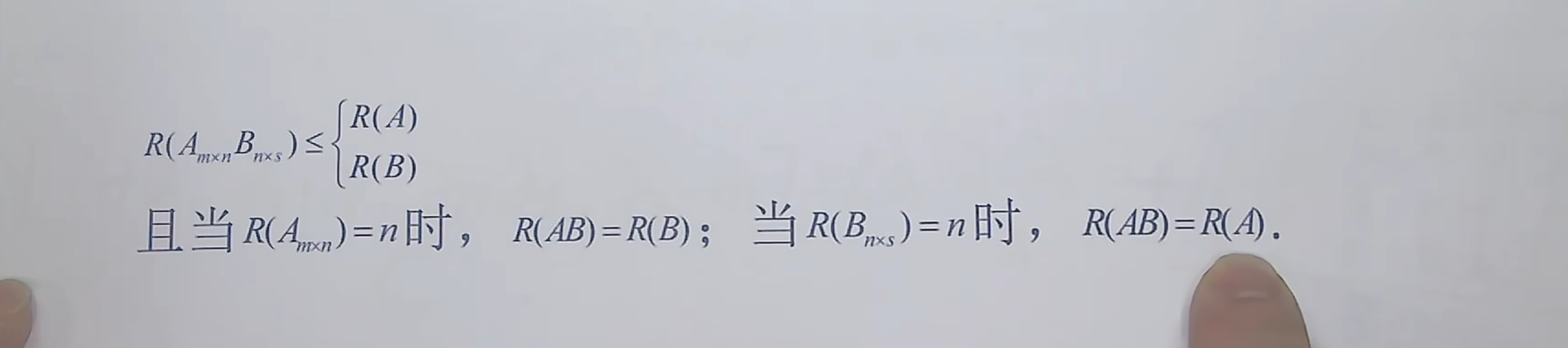
两个矩阵相乘,谁的秩=链接的n这个数字的大小,那么就不会改变原本矩阵的秩,即原本矩阵的秩一定为R(AB)=R(A) 或者 R(B)
比如该题,B的秩=2
A已知线性无关,则线性无关的向量组不会改变原本矩阵的秩,而原本矩阵的秩就等于R(B)=2故C线性无关

方程组的行向量意义解读
遇见正交相关题目可以往上面靠


同解方程组和矩阵的联系

解释如下所示,当Ⅰ的解也是Ⅱ的解的时候,就说明当联立方程组时
如下所示的[AX,BX]T的时候
B加入进来没有影响原本的方程组的解的关系,那也就是说,B实际上能够被A表示也就是说能够通过初等行列变换变化将B变为0,即没有增添新的约束改变方程组的解空间
即同解方程组行向量能够互相线性表示

向量组等价和矩阵等价的区别和联系

其中还有若向量组能表示对方,且秩相等,则两个向量组等价
线性方程组中行满秩和列满秩和方程组的对应关系
若一个方程组行满秩那么该方程组一定有解,若A为m×n矩阵那么说明m<=n
所以该列向量在n>m的时候线性相关
对于一个方程组来说,若列满秩则说明该方程组无解或者拥有唯一解
这里的有解和无解都是在齐次线性方程组的情况下


遇到这种不好计算的题目就直接求行列式计算

线性方程组和几何平面的关系
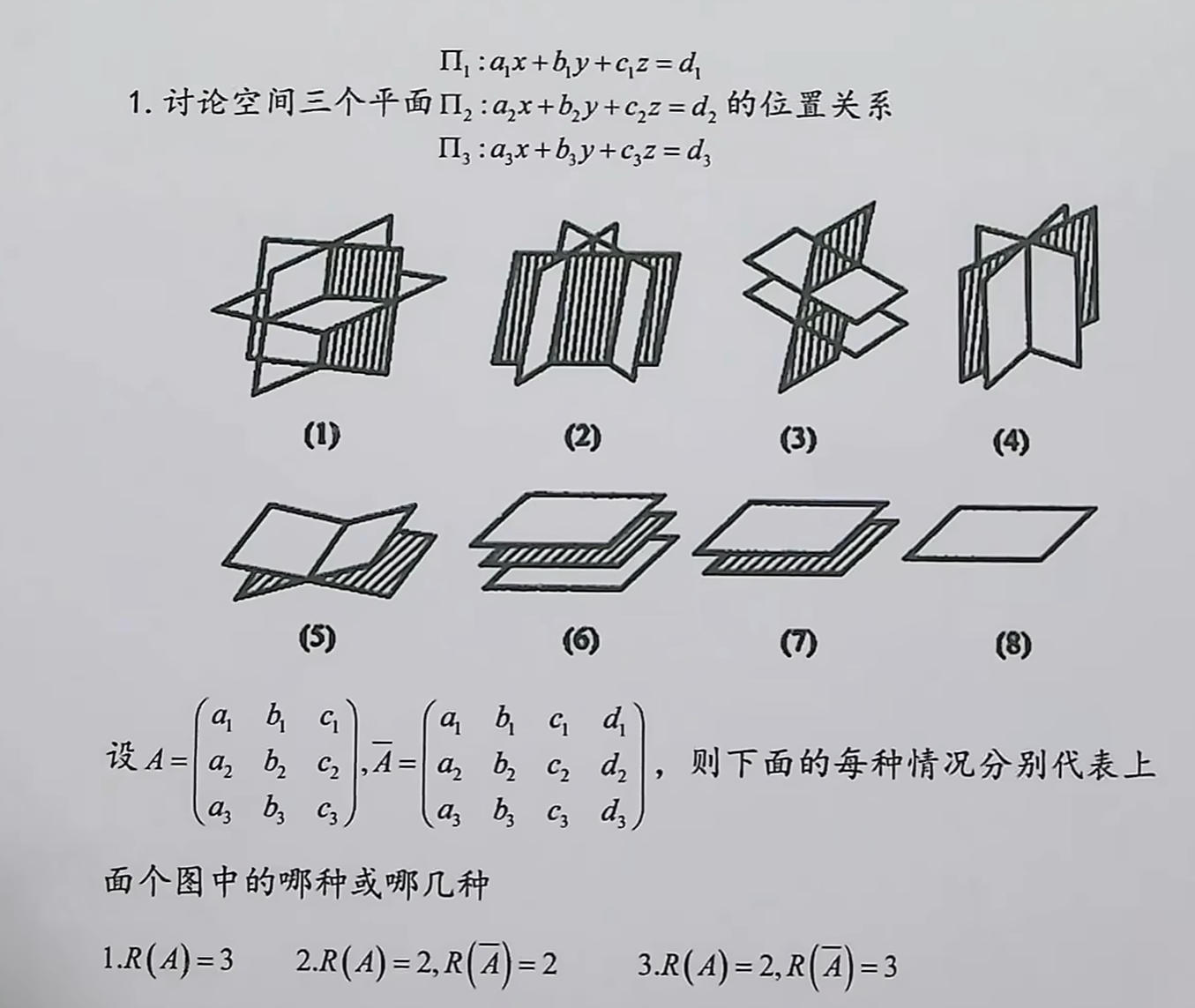

以该题作为分析,如果相交于一个直线那么只有可能是5即有两个平面重合,一个平面于这两相交构成了一个平面,即有两个有效约束,那么就是秩=2

同解方程组和行向量的联系

正交矩阵
其性质如下
正交矩阵还有一个重要的性质,就是矩阵的某列向量做内积得到的一定是一个单位向量即
这种形式


矩阵相似
告诉你特征值和特征向量的出题方式
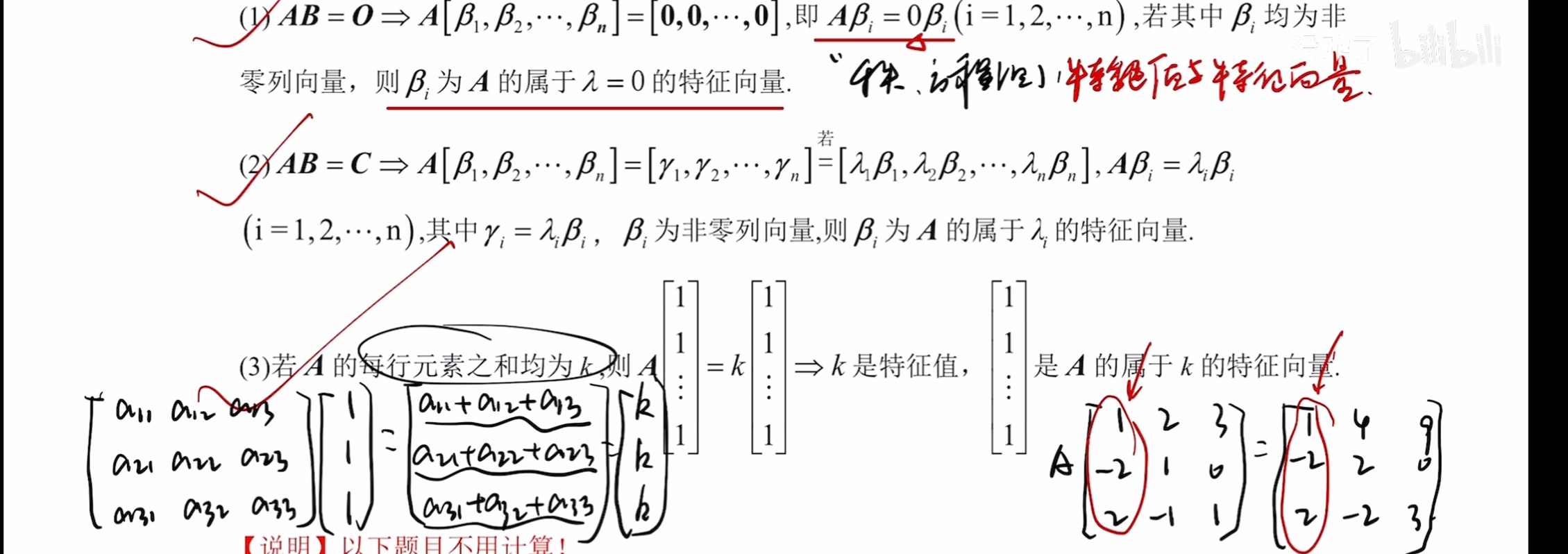
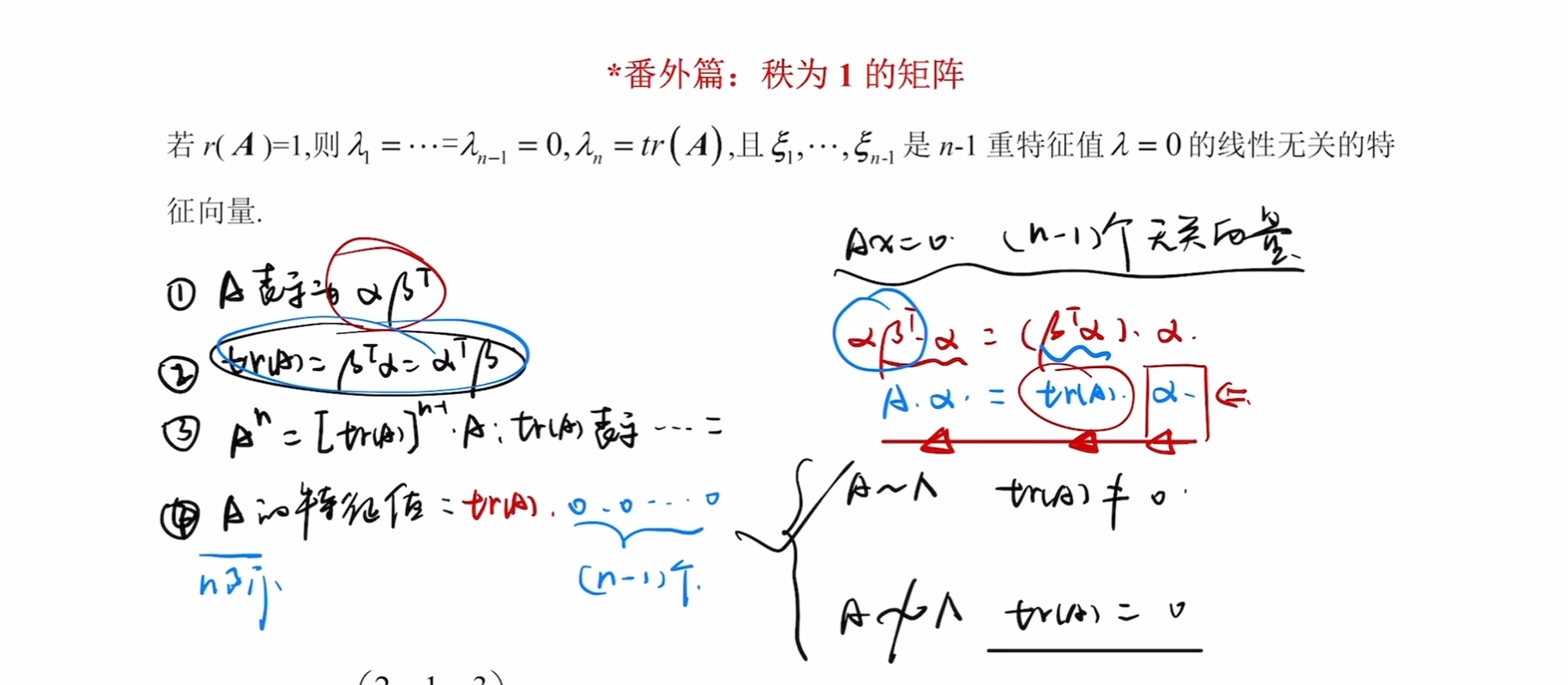
秩1矩阵的相似特性
三角矩阵的特征值就是其对角元素
相似对角化的必要条件

两矩阵相似的必要条件
其中还有


其中该条件也是必要条件
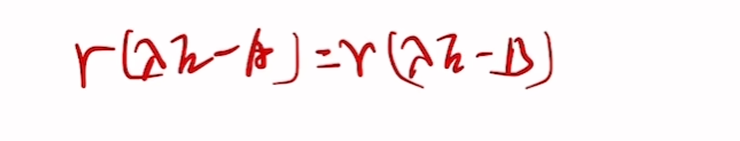

矩阵的合同

重要错题
对于该题,我们可以得知E-2aaT一定是一个可逆矩阵,因为其特征值全部不为0所以该矩阵可逆
然后我们对题目的式子转置
令E-2aaT=C
则转置后变成了CTA=B
又因为C可逆,所以作用于A不会改变其A行向量间性质,又因为行向量等价,方程组等价,所以同解

