数字信号处理 第一章(离散时间信号与系统)【上】
参考教程:https://www.bilibili.com/video/BV1qTCDYpEFr?spm_id_from=333.788.videopod.sections&vd_source=8f8a7bd7765d52551c498d7eaed8acd5
一、概述
1、信号的分类
(1)按照维度可划分为:
①一维信号——如音频信号。
②二维信号——如图像信号。
③多维矢量信号。
(2)按照是否能确定可划分为:
①确定性信号:若信号在任意时刻的取值能精确确定,则称它为确定性信号,它的值可以用有限个参量来唯一地加以描述,如直流信号、阶跃信号、正弦波信号等都是确定信号。
②随机信号:若信号不能用有限的参量来唯一描述在任意时刻的取值,或者说取值是随机的,而且也无法对它的未来值确定性地预测,则称它为随机信号,随机信号一般是通过统计学的方法来描述的。
(3)按照连续性可划分为:
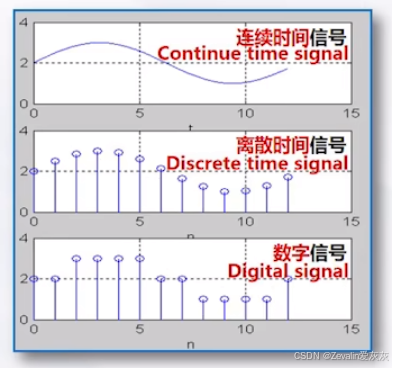
①连续时间信号:随时间连续变化的信号,它们在一个区间例的任何瞬间都有确定的值。
②离散时间信号:只在离散的时间点有确定的值,通常是对连续信号进行采样得到的。
③数字信号:时间上离散、幅度上量化后的信号,它可用一系列的数表示,而每个数又可表示为二进制码的形式。
2、信号处理系统的基本组成
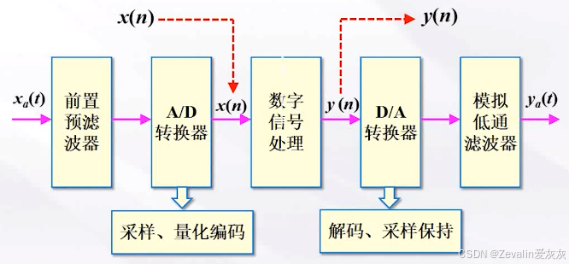
信号处理系统的基本组成如下图所示,其中数字信号处理的主要特点是——精度高、灵活性高、可靠性高。
3、数字信号处理的学科概貌
(1)信号的采集(A/D)技术、采样定理、量化噪声分析。
(2)离散信号的分析——时域及频域分析、各种变换技术、信号特征的描述等。
(3)离散系统分析——系统的描述、系统的单位取样响应、系统函数及频率特性。
(4)信号处理中的快速算法——快速傅里叶变换、快速卷积与相关。
(5)信号的估值——各种估值理论、相关函数与功率谱估计。
(6)滤波技术——经典数字滤波器设计、现代数字滤波器设计。
(7)信号的建模——AR、MA、ARMA模型。
(8)信号处理中的特殊算法——如抽取、插值、反卷积、信号重建。
(9)信号处理技术的实现——软件实现、硬件实现。
二、离散时间信号——序列
1、离散时间信号的由来
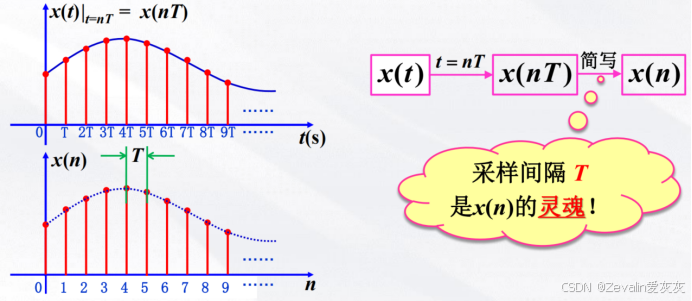
(1)离散时间信号(又称序列)是连续时间信号以时间T等间隔采样得到的,T称为采样周期或采样间隔。
(2)连续的信号对计算机而言数据量是无穷大的,计算机只能处理离散的数据,所以需要对连续的信号进行离散化,以便计算机处理。
(3)采样间隔T(或者说采样频率)的选取与信号变化快慢有关,一般需要遵守,其中
为采样频率,
为带限信号的最高频率分量。
2、离散时间信号的表达
(1)一般来说,采样间隔是均匀的,可以用x(nT)表示信号在nT点上的值,n为整数。
(2)由于x(nT)顺序地存放在计算机存储器中,为了表示方便,通常用x(n)表示离散时间信号的序列值,只要明确采样间隔T的值,就可以直接用n作为数据索引方便计算机处理。
3、离散时间信号的表示方法
(1)用数列表示离散时间信号:
用大括号将数列中的元素括起,逗号将各元素分隔,即可表示离散时间信号,一般默认数列首元素对应处的采样值,也可以用下划线将对应
处的采样值特别标识
![]()
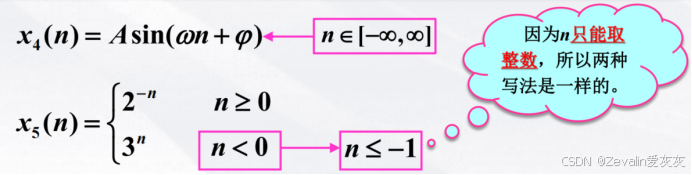
(2)用函数表示离散时间信号:
离散信号同样可以用函数表示,只是不同的是,离散函数中n只能取整数,而连续函数则是可以在其定义域内任意选取
(3)用图形表示离散时间信号:
既然连续函数可以用图形表示,那么离散函数自然也可以,如下图所示,图中横坐标n表示离散的时间坐标,仅在n为整数时才有意义,纵坐标代表信号的值
绘图时需注意,必须标明横坐标和纵坐标的label,注明原点的位置,注明每个时间坐标下的信号值
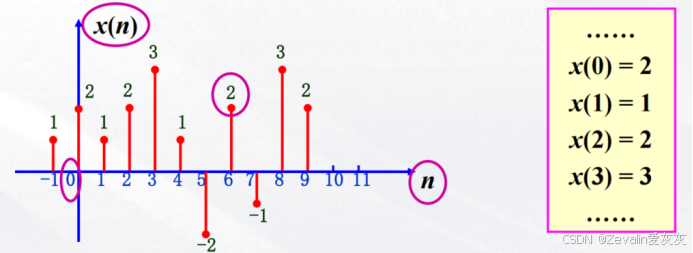
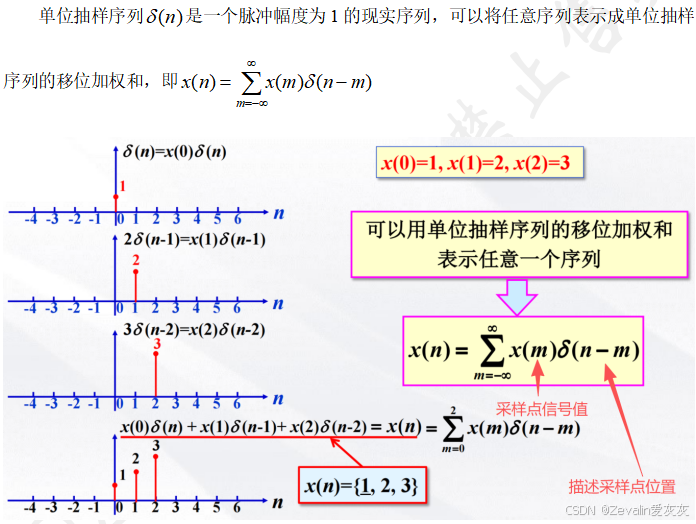
(4)用单位抽样序列表示离散时间信号:
4、离散时间信号的基本运算
(1)序列的和:
两序列的和是指同序号n的序列值逐项对应相加而构成的新序列

(2)序列的积:
两序列的积是指同序号n的序列值逐项对应相乘而构成的新序列
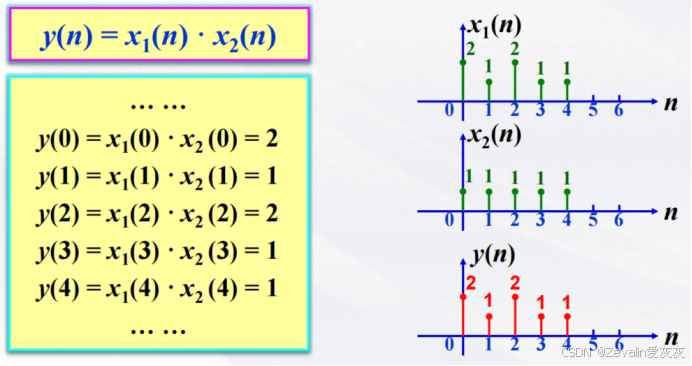
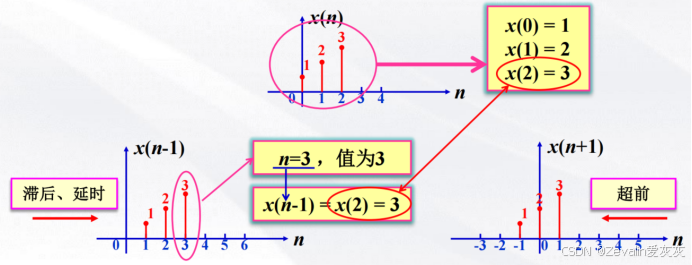
(3)序列的移位:
设有一序列x(n),当m>0时,x(n-m)表示序列x(n)逐项依次右移m位后得到的序列,x(n+m)表示序列x(n)逐项依次左移m位后得到的序列
要想确认人算的移位后序列是否无误,可直接用原数列的信号值进行验证
需要说明的是,延时单元可以将以前的某采样时刻的数据暂存奇力,参与这个时刻的运算,比如回声可以用延迟单元来生成,直接声音和它延迟了R个周期的单个回声求和即可生成(为回声的衰减系数,值域为(0,1)),即
,当然,增加项数可以生成多重回声
(4)序列的反褶:
设有一序列x(n),则x(-n)是以n=0位纵轴将x(n)反褶后的序列

谨记,对序列的移位和反褶,都是施加在n上的,与n已经有的偏移或系数无关
(5)累加和:
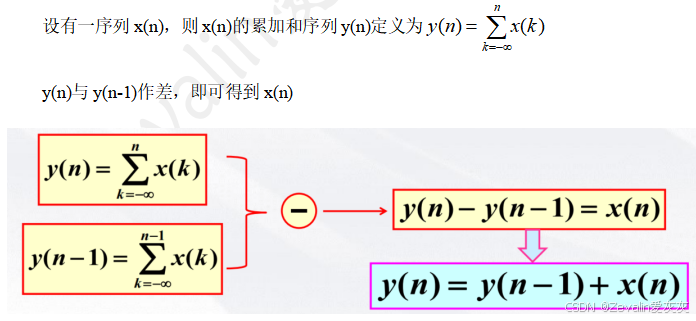
(6)差分运算:

(7)序列的时间尺度(比例)变化:
设有一序列x(n),则其时间尺度变换序列为x(mn)或x(n/m),m为正整数
x(mn)为抽取序列,求解的过程又叫下采样;x(n/m)为插值序列,求解的过程又叫上采样
(8)序列的能量:
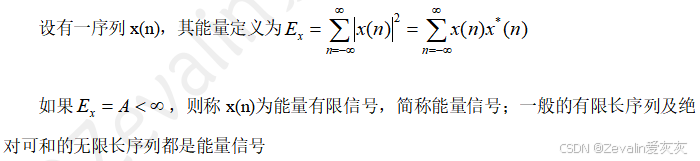
(9)序列的平均功率:

5、MATLAB下序列运算的实现方法
(1)例程:用MATLAB产生并画出单位抽样序列。
%确定位置向量(横坐标)的显示范围
n = -10:20;%确定与位置向量(横坐标)匹配的δ(n)(纵坐标),用全零矩阵生成非1点即可
delta = [zeros(1,10) 1 zeros(1,20)];%画出δ(n)
stem(n, delta);%图中显示网格
grid on;%增加坐标标识和图名
xlabel('Time index n'); ylabel('Amplitude');
title('Unit Sample Sequence');%调整坐标显示范围
axis([-10 20 0 1.2]);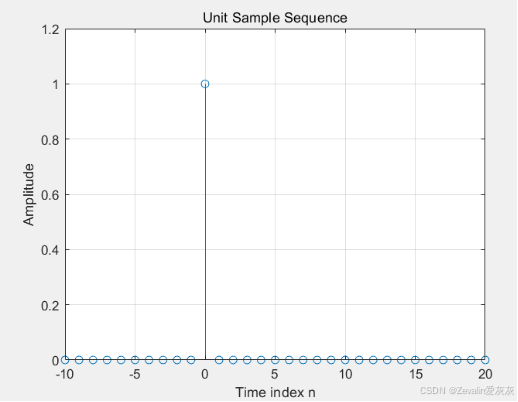
(2)例程:定义函数生成单位抽样序列。
function [x,n] = impesq(np,ns,nf) %np为位移量,ns为n的取值下限,nf为n的取值上限%检查输入参数正确性
if ( (np < ns) | (np > nf) | (ns > nf) )
error('参数必须满足 ns <= np <= nf')
end%生成序列横坐标n
n = [ns:nf];%生成序列纵坐标x
x = [ (n-np) == 0];(3)例程:定义函数实现序列相加。
function [y,n] = seqadd(x1,n1,x2,n2) %参数分别为序列纵坐标集和序列横坐标集%确定相加后序列的横坐标集(原序列的横坐标集不一定相同,新序列的横坐标集需要将两个原序列的横坐标集全部包含)
n = min(min(n1), min(n2) ) : max(max(n1), max(n2) );%按照得到的横坐标集创建两个等长新序列
y1 = zeros(1, length(n) );
y2 = zeros(1, length(n) );%将两个原序列分别放在两个新序列中,横坐标要与新序列对应
y1(find( (n >= min(n1) ) & (n <= max(n1) ) ) ) = x1;
y2(find( (n >= min(n1) ) & (n <= max(n1) ) ) ) = x2;%两个调整好位置的等长新序列相加,得到原序列相加结果
y = y1 + y2;(4)例程:定义函数实现序列相乘。
function [y,n] = seqmult(x1,n1,x2,n2) %参数分别为序列纵坐标集和序列横坐标集%确定相乘后序列的横坐标集(原序列的横坐标集不一定相同,新序列的横坐标集需要将两个原序列的横坐标集全部包含)
n = min(min(n1), min(n2) ) : max(max(n1), max(n2) );%按照得到的横坐标集创建两个等长新序列
y1 = zeros(1, length(n) );
y2 = zeros(1, length(n) );%将两个原序列分别放在两个新序列中,横坐标要与新序列对应
y1(find( (n >= min(n1) ) & (n <= max(n1) ) ) ) = x1;
y2(find( (n >= min(n1) ) & (n <= max(n1) ) ) ) = x2;%两个调整好位置的等长新序列相乘,得到原序列相乘结果,注意需要使用点乘,否则MATLAB会执行矩阵运算
y = y1 .* y2;(5)例程:定义函数实现序列移位。
function [y,ny] = seqshift(x,nx,m) %参数分别原序列纵坐标集、原序列横坐标集和位移量%对横坐标集每个元素全部加m,得到新序列的横坐标集
ny = nx + m;%新序列的纵坐标集与原序列相比无变化
y = x;(6)例程:定义函数实现序列反褶。
function [y,ny] = seqfold(x,n) %参数分别原序列纵坐标集、原序列横坐标集%对原序列纵坐标集做逆转,赋给新序列纵坐标集
y =fliplr(x);%对原序列横坐标集做逆转,修改正负号使逆转序列递增,再赋给新序列横坐标集
ny = -fliplr(n);6、几种常用的典型序列
(1)单位抽样序列:

(2)单位阶跃序列:
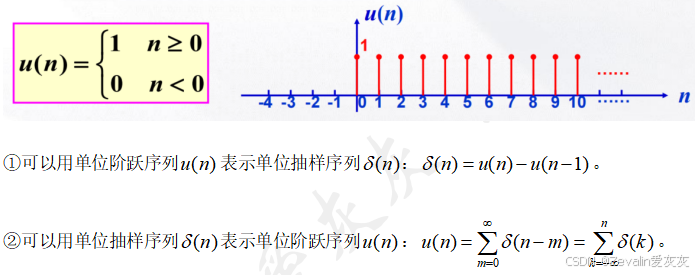
(3)矩形序列:

(4)实指数序列:
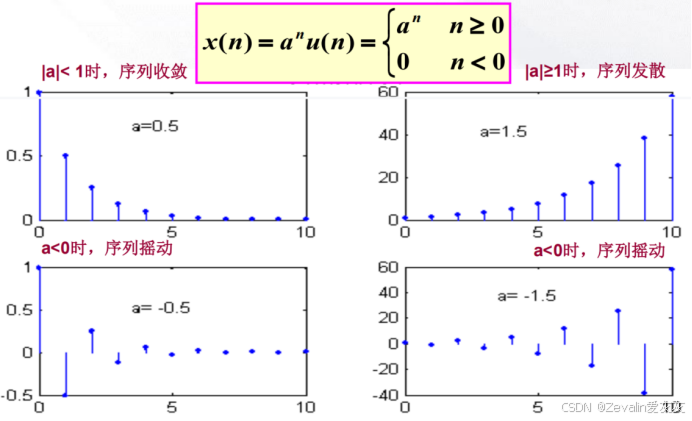
(5)正弦序列:

(6)复指数序列:

7、序列的周期性


三、离散时间系统
1、离散系统的线性性质
(1)线性系统是满足叠加原理的系统:
①可加性:
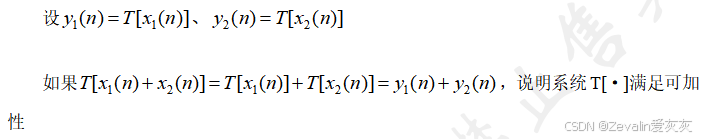
②比例性(齐次性):

(2)结合上面的描述,线性系统应满足
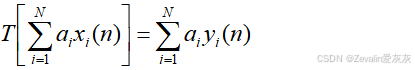
(3)线性系统必须满足零输入产生零输出,当然,如果某个系统满足零输入产生零输出,它也不一定是线性系统,需要进一步验证它是否满足叠加定理。
(4)举例:
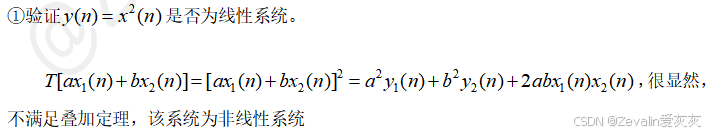

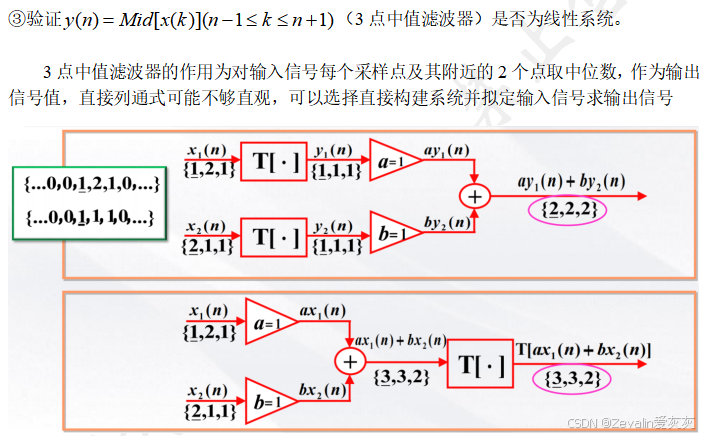
2、离散系统的移不变性质




3、LSI系统的时域求解——线性卷积方法



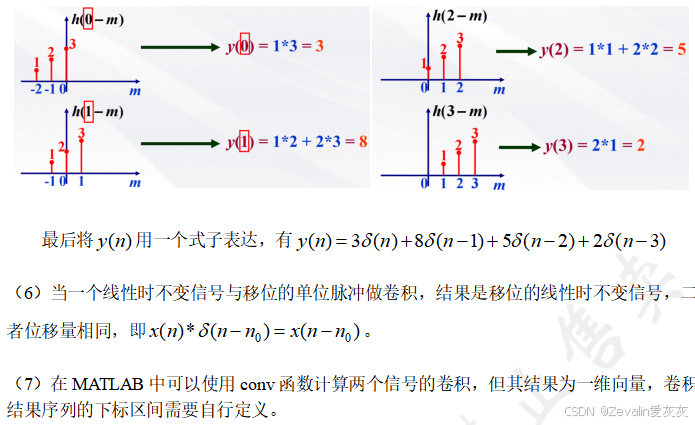
%定义信号
nx = [0:1]; x = [1 2];
nh = [0:2]; h = [3 2 1];%卷积计算
y = conv(x, h);
ny = [0:3];%画图
subplot(311); stem(nx,x,'linewidth',2);
axis([min(ny) max(ny) 0 max(y)]); grid on;
subplot(312); stem(nh,h,'linewidth',2);
axis([min(ny) max(ny) 0 max(y)]); grid on;
subplot(313); stem(ny,y,'linewidth',2);
axis([min(ny) max(ny) 0 max(y)]); grid on;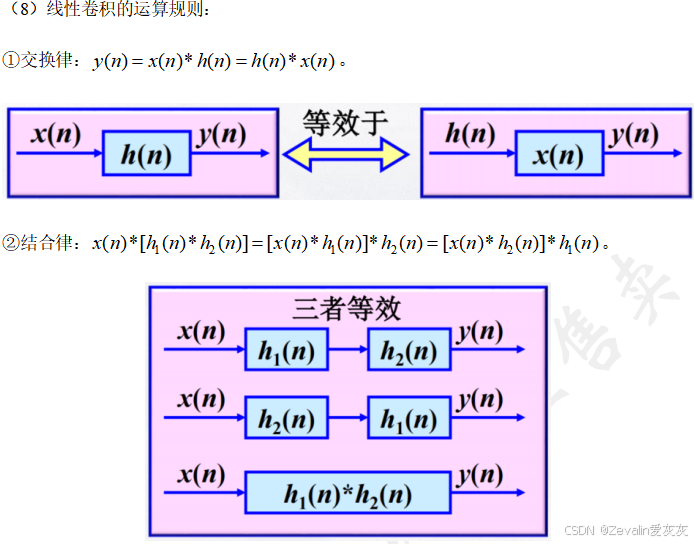
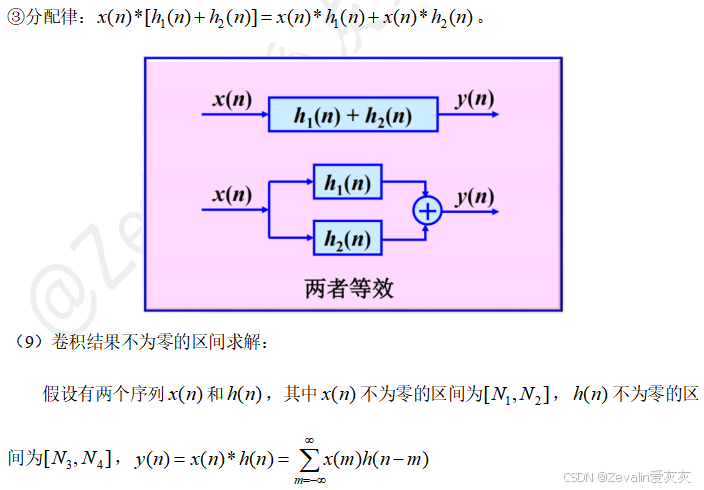
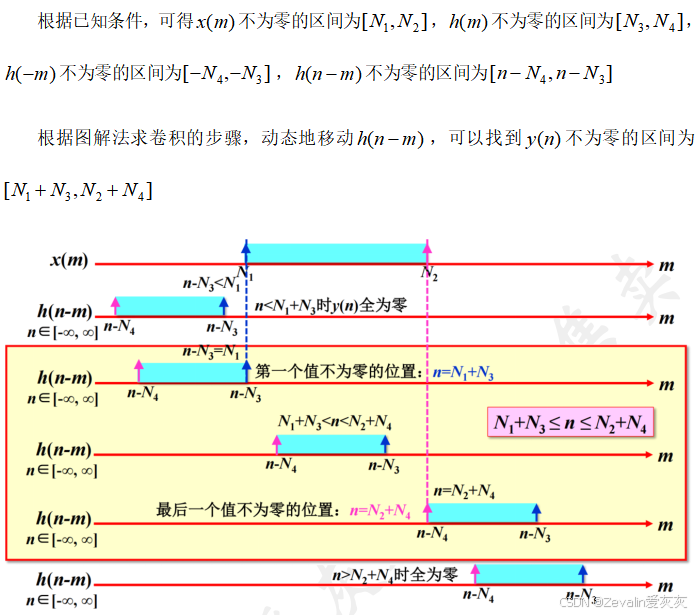

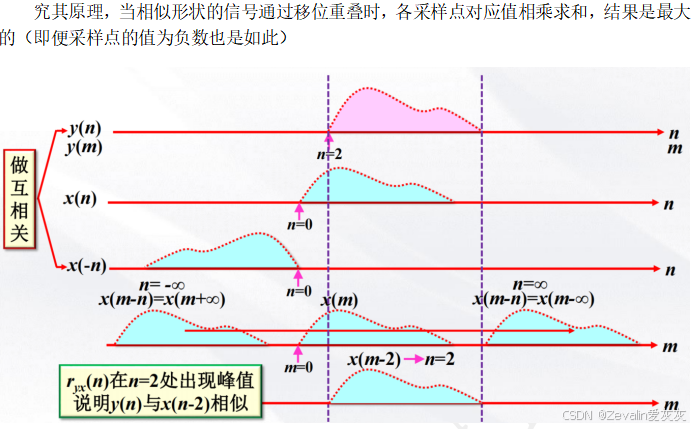
4、离散时间系统因果性及稳定性
(1)一般系统的因果性定义及判断方法:

(2)一般系统的稳定性定义及判断方法:

